大型动力翼伞拖曳起飞动力学研究

苏浩东 滕海山 刘宇 吴卓

大型动力翼伞拖曳起飞动力学研究

苏浩东1,2滕海山1,2刘宇1,2吴卓1,2

（1北京空间机电研究所，北京 100094）（2中国航天科技集团有限公司航天进入、减速与着陆技术实验室，北京 100094）

动力翼伞具有有效载荷大、续航时间长、安全性和可靠性高以及成本低等优点，在军用和民用领域有很大的发展潜力。文章针对动力翼伞的地面拖曳起飞过程，根据牛顿力学的基本原理，建立了动力翼伞拖曳起飞纵向动力学模型，描述了翼伞拖曳、稳定、放飞过程的运动状态，搭建了动力翼伞运动过程的仿真环境，分别模拟了拖曳过程与放飞后翼伞的运动状态。通过控制变量比较了翼伞在不同运动参数下的稳定情况，给出了动力翼伞释放的速度、角速度以及角度条件，得出了地面拖曳车辆的合理运动模式及动力翼伞释放时机，对于后续动力翼伞的工程应用具有一定的指导意义。

拖曳起飞 动力学仿真 翼伞摆角 拖曳车运动 动力翼伞

0 引言

动力翼伞是在冲压翼伞的基础上发展而来，继承了翼伞优良的气动特性、飞行性能和无人机的控制性能，相较于其他种类的无人机，动力翼伞具有飞行平稳，可控性强，安全可靠与成本低等优势，已经逐渐应用于农林植保、物资投送等军民用领域[1]。

近年来，国内外关于动力翼伞的研究主要集中在中小型翼伞的动力学仿真与控制上。进行动力翼伞的研究，首先需要分析其动力学特性，动力翼伞的运动过程主要有起飞、爬升、巡航、转弯、下降与着陆5个阶段。针对这5个阶段，国内外的研究者进行了不同自由度下翼伞的动力学建模与仿真[2-10]。杨华建立了动力翼伞纵向四自由度动力学模型，提出了通过降落阶段短暂的动力操纵实现雀降的新方法[11]；康鹤云建立了动力翼伞六自由度动力学模型，全面分析了动力翼伞平飞、爬升、转弯等主要飞行性能，分析了动力翼伞的展弦比、安装角等对飞行性能的影响[12]；GORMAN建立了翼伞系统的七自由度模型，在仿真分析之后发现，翼伞转弯时，七自由度模型比六自由度模型产生的相对偏航角的变化更为显著[13]；胡文治对翼伞系统采用九自由度动力学建模进行计算，通过仿真得到翼伞系统的滑翔、雀降、转弯等基本运动特性，分析了翼伞安装角、空投物质量、空投物阻力特征等参数对翼伞系统飞行性能的影响[14]；OCHI提出翼伞九自由度非线性飞行动力学模型，研究了伞面相对于有效载荷进行滚转运动的转弯性能[15]；蒋万松等基于可控翼伞回收技术的火箭助推器—控制平台—翼伞多体飞行系统为研究对象，采用拉格朗日建立了三体组合十自由度多体动力学仿真模型，通过仿真与试验的对比分析飞行机理和系统性能[16]；张青斌等采用拟坐标形式的拉格朗日方程，提出反映翼伞连接方式和相对运动的翼伞多体动力学建模方法，建立了四体十八自由度动力学模型，有效反映了翼伞系统的相对运动[17]。

迄今为止，国内外对于一般冲压翼伞的建模与仿真水平已经非常成熟，对于动力翼伞也实现了多方面的应用，但对于大型动力翼伞的理论研究还比较匮乏，尤其是针对动力翼伞地面放飞过程及拖曳起飞的动力学研究仍属空白。与小型翼伞飞行器相比，大型动力翼伞的动力学与控制原理基本与之相同，但使用更大的冲压翼伞作为机翼，往往需要更大马力的发动机来匹配，对控制的要求也更高，另外对于气动性能、飞行力学等方面的理论也需要进一步研究与试验验证[18-22]。

本文以某大型动力翼伞（面积为300 m2）为研究对象，通过地面车辆拖曳的方式放飞翼伞，建立了描述动力翼伞拖曳起飞过程的纵向动力学模型，根据已经得到的升阻力系数与压心条件仿真分析了拖曳起飞过程中，翼伞在不同初速度、角速度以及摆角下放飞的运动情况，获得了拖曳运动规律以及动力翼伞的起飞释放条件，为大型动力翼伞的设计研究提供参考。

1 纵向动力学建模

1.1 建模对象

本文所研究的大型动力翼伞的伞系统为已研制成功的300 m2冲压翼伞，建模对象为拖曳与起飞过程的翼伞–机身系统，机身部分等效为长方体结构，带有螺旋桨推进系统，推力设定为8 000 N，系统整体在起飞前固定于拖曳车后方。拖曳过程为，汽车以一定加速度运动至一定速度，翼伞受牵引的作用升起并逐渐稳定，当升力达到可以克服系统重力并且翼伞稳定时，则放飞动力翼伞，进而动力翼伞靠自身发动机推力爬升。系统整体外形如图1所示。

图1 动力翼伞起飞系统示意图

图2 机身–翼伞纵向简化模型

假设翼伞在拖曳运动过程中伞绳与翼伞始终为一个整体，只有绕连接点的转动与随机身的平动，推力方向过机身质心且与机身轴线平行，机身的升阻力均忽略不计。

1.2 动力学方程建立

对翼伞进行纵向动力学建模（见图2），分别以p和f为原点建立坐标系，其中伞轴系的1轴平行翼伞弦向指向前缘，机身轴系的2轴平行于机身轴线向前，1轴垂直于1轴，2轴垂直于2轴。

假设在拖曳阶段，机身与拖曳车固连做匀加速直线运动，则翼伞的运动为绕连接点的转动和随机身的水平运动。列写翼伞的运动学方程为

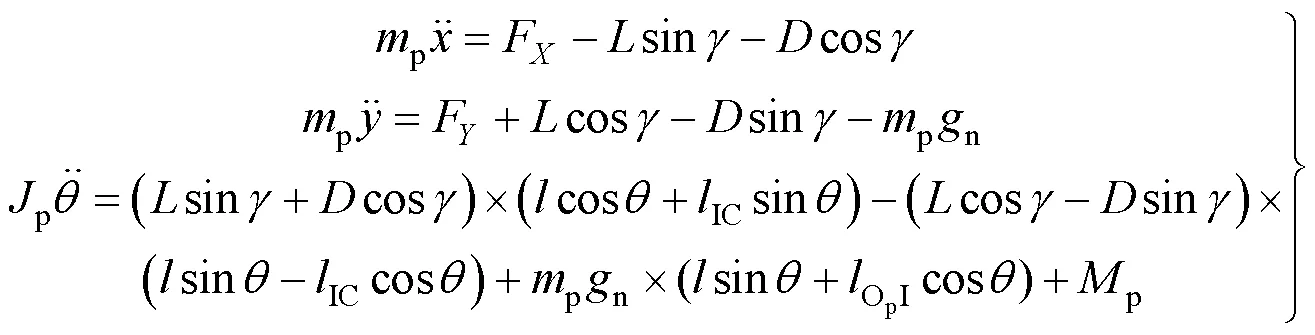
式中1为翼伞绕质心转动惯量。

对于放飞时刻，拖曳车不再对系统施加力的作用，转而机身发动机开启推力作用，因此考虑发动机推力的作用即可得到动力翼伞放飞时刻的动力学方程

式中2为机身绕质心转动惯量。

1.3 外力求解

考虑拖曳过程中汽车加速度和汽车质量v为已知，将汽车与机身看作整体，考虑翼伞对车身的拉力作用，可以写出汽车水平方向的运动方程为

式中t为汽车发动机推力；r为汽车所受阻力；J为伞绳拉力。将系统看作整体，系统水平方向的运动方程为

联立式（4）和式（5），可以得到伞绳拉力的大小为

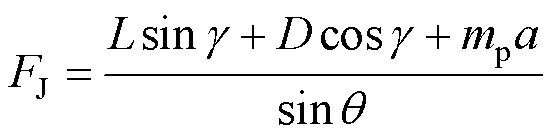
此外，翼伞的升阻力可表示为

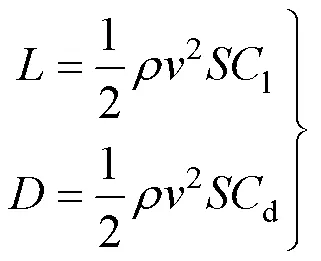
式中为空气密度；为翼伞速度；为翼伞面积；l为升力系数；d为阻力系数。

1.4 附加质量求解

附加质量对翼伞等轻载飞行器的飞行动力学有很大影响，其值有时可以达到飞行器本体质量的4～5倍，因此在研究的翼伞运动时其附加质量力不能忽略。本文对于附加质量的求解采用Lissaman估算方法[23]，由于本文只考虑翼伞起飞过程的纵向平面运动，因此只需要用到三个估算公式，如下

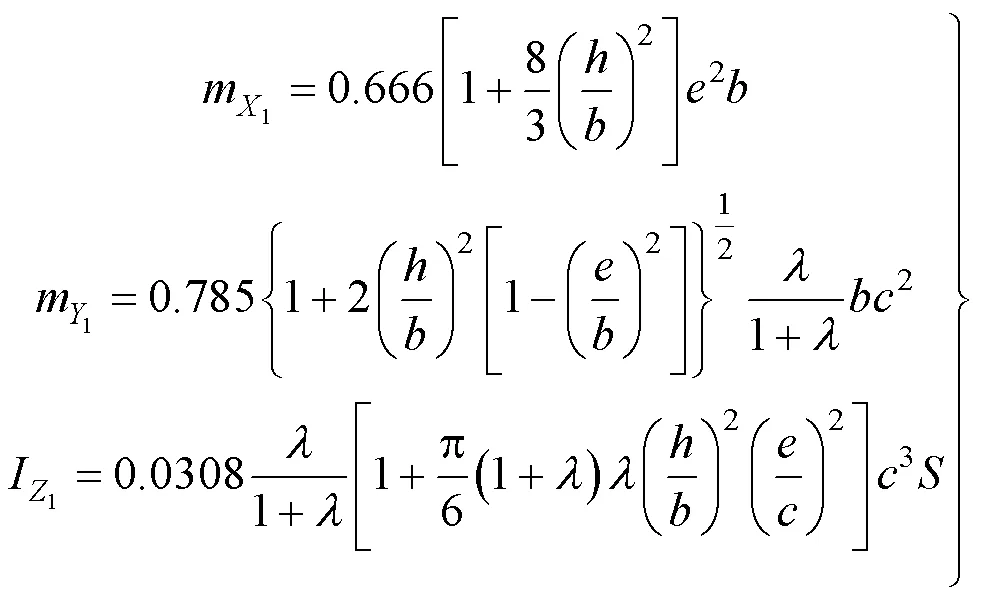
式中 和为翼伞附加质量沿伞轴系X1轴与Y1轴方向的分量；为翼伞绕Z1轴的附加转动惯量分量；h为翼伞高度；b为翼伞展长；c为翼伞弦长；e为翼型厚度；展弦比λ=b/c。翼伞几何尺寸示意，如图3所示。

由于翼伞的纵向运动造成的周围流体动能变化，动能为

则翼伞对流体的冲量F和冲量矩M为

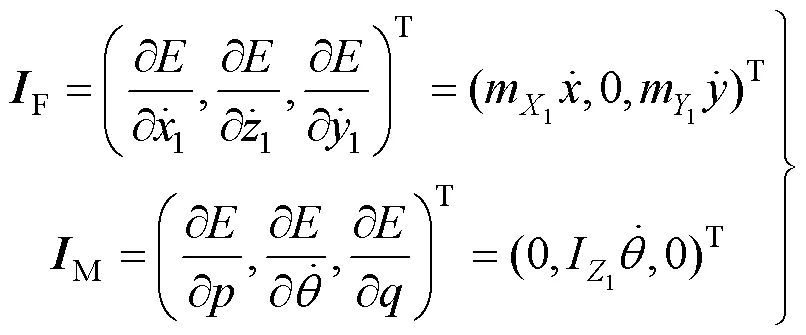
式中1、1、1分别为翼伞沿1轴、1轴、1轴方向的位移分量；为翼伞绕1轴旋转角速度；为翼伞绕1轴旋转角速度。

流体对伞体的附加质量力a和附加力矩a为

2 仿真分析

动力翼伞起飞过程主要经历地面拖曳与放飞两个过程，其中地面拖曳过程需要满足放飞的初始条件，即动力翼伞经过一段时间的地面拖曳所达到的水平速度、摆动角速度和攻角等运动状态参数满足翼伞能够成功放飞的初始条件。本文搭建了动力翼伞拖曳以及起飞过程的动力学模型，求解动力翼伞放飞条件以及拖曳过程运动参数。

表1 大型动力翼伞主要设计参数

Tab.1 Main design parameters of large power parafoil

2.1 仿真参数

本文针对大型动力翼伞拖曳起飞系统，根据300 m2大型翼伞设计要求确定其主要设计参数，见表1。

另外，采用有限元仿真获得300 m2冲压翼伞的气动参数见图4。从图4（a）中可以看出随着攻角变大，升力系数先增大后减小，在40°攻角时升力系数最大。从图4（b）中可以看出压心位置距离前缘先靠近然后逐渐远离。

图4 300 m2翼伞气动参数

2.2 放飞条件分析

其中，

将式（8）代入，则

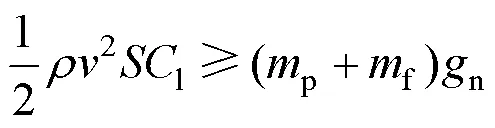
其次，考虑在不同初速度下放飞翼伞后翼伞的运动情况，通过改变程序中速度变量得到在不同初速度下50 s内翼伞的运动状态，如图5所示。

由图5（a）和图5（f）可以看出，动力翼伞初速度小于4 m/s大于18 m/s时，翼伞攻角先短暂浮动后快速减小，即翼伞短暂摆动后向下俯冲，无法起飞。而在两者之间的其他速度时，翼伞攻角均可收敛至10°左右，且图5（d）中攻角的变化范围不超过1°，即在初速度为12 m/s时翼伞的摆动幅度最小。

除了要求翼伞“飞得起”之外，“飞得稳”同样至关重要。动力翼伞在放飞后能否飞行平稳的关键还在于，放飞时刻翼伞的摆角大小与摆动角速度的大小及方向。

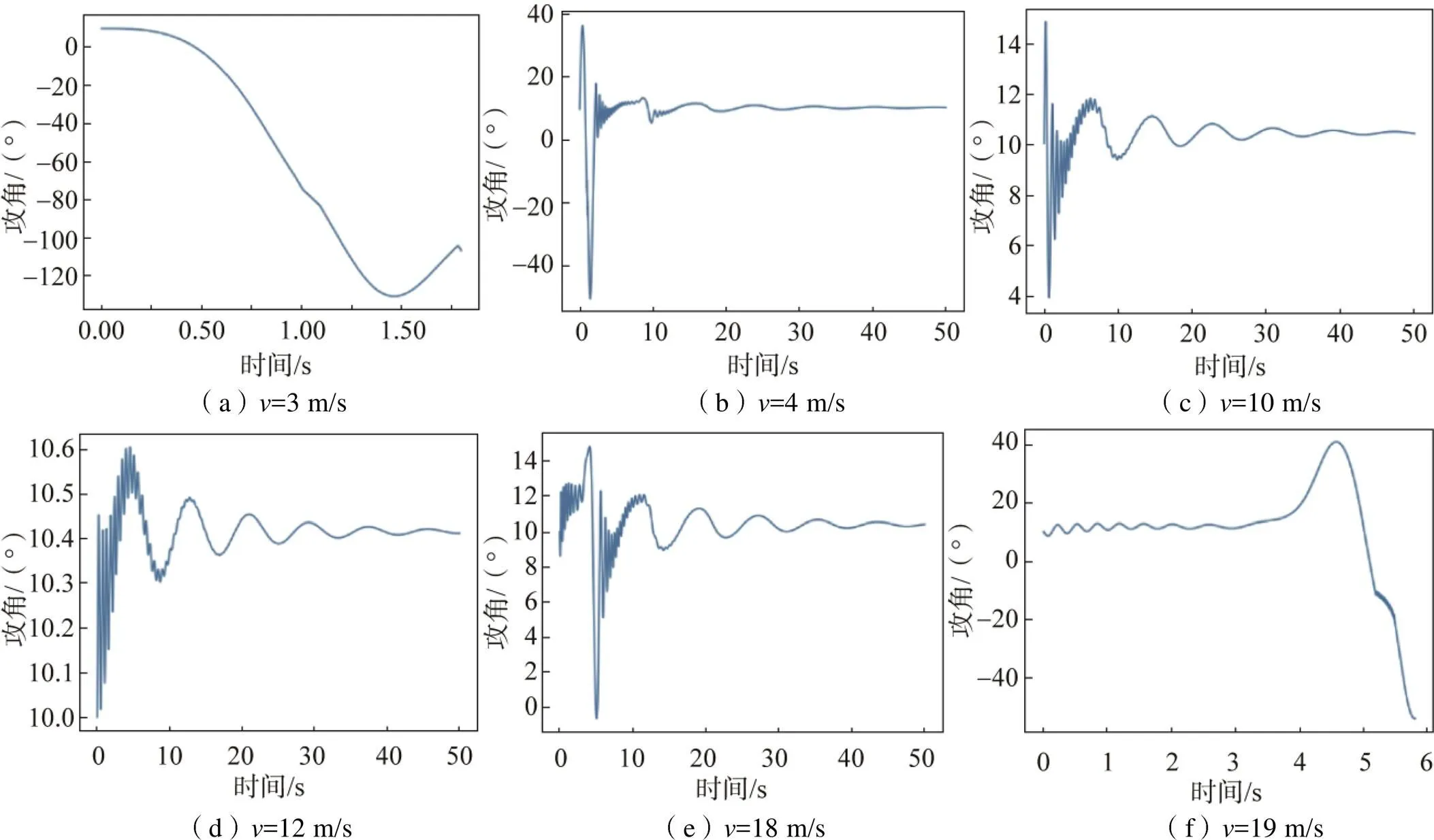
图5 不同初速度下放飞翼伞的攻角变化

如图6所示，翼伞放飞时刻对应一个当前翼伞的摆角（翼伞绕连接点转动与竖直方向的夹角），不同的摆角对应不同的起飞姿态，不同摆角下起飞对于当前翼伞绕连接点摆动角速度也有一定的要求。研究发现，当起飞时刻翼伞摆角较小时，摆动角速度越小起飞越稳定，超过某一角速度值则发生倾覆。当起飞时刻翼伞摆角较大时，若有一定方向和大小的角速度，翼伞也可以正常放飞。为了研究翼伞放飞时刻的摆角与角速度条件，本文进行了仿真验证。

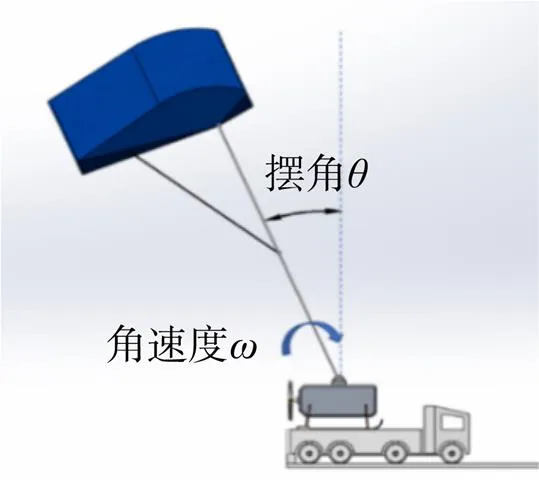
图6 翼伞摆角与角速度

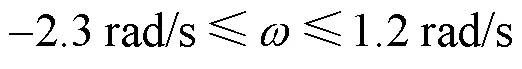
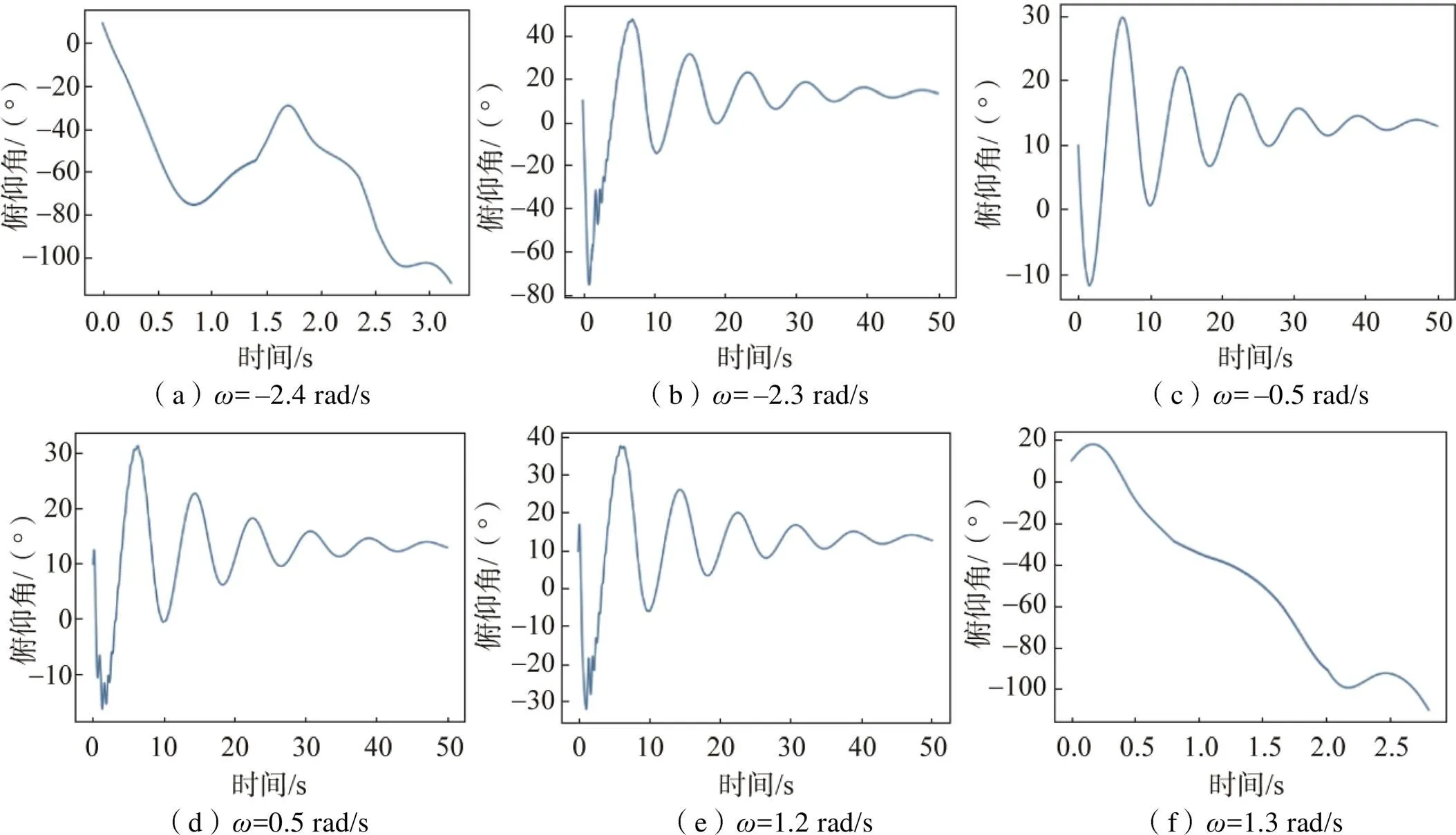
图7 不同初始角速度下放飞翼伞的俯仰角变化

此外，若起飞时刻摆角过大，则无论摆动角速度的大小，翼伞均无法正常起飞。在仿真过程中，不断增大起飞时刻的摆角大小，研究不同摆角下放飞翼伞的区别，发现当起飞时刻摆角小于–17°或大于20°时，翼伞运动曲线无法收敛，即飞行器不能正常起飞。只有当起飞时刻的翼伞摆角在–17°～20°的范围内，翼伞攻角才可在合适的角速度范围内正常收敛，如图8所示。

图8 翼伞起飞时刻摆角范围

表2 不同摆角起飞所允许的角速度

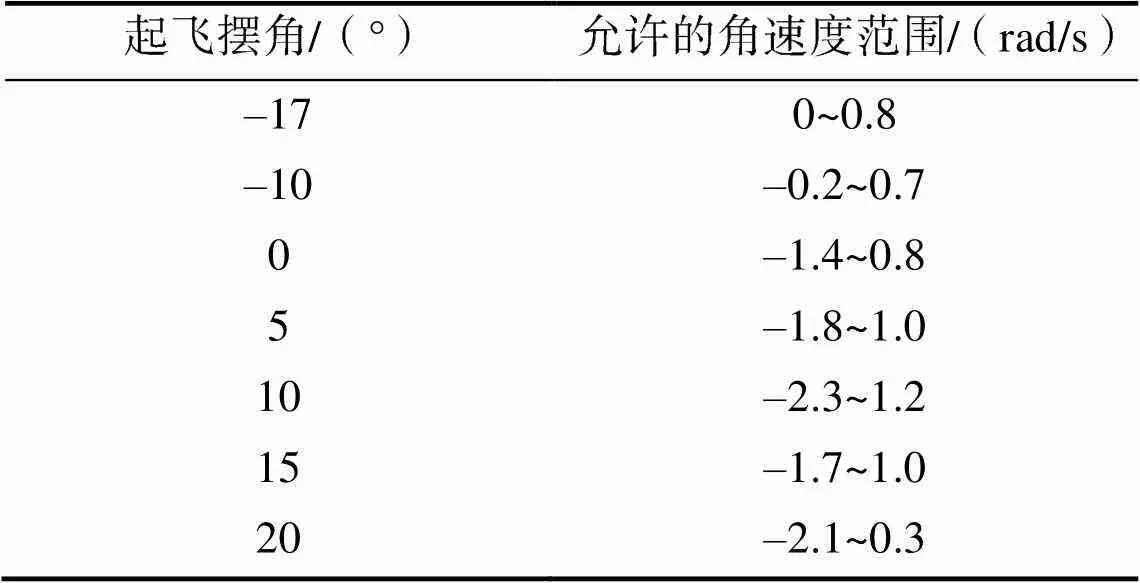
Tab.2 Angular velocity allowed for take-off at different pendulum angles

仿真得到的不同摆角起飞下允许的角速度范围，如表2所示。

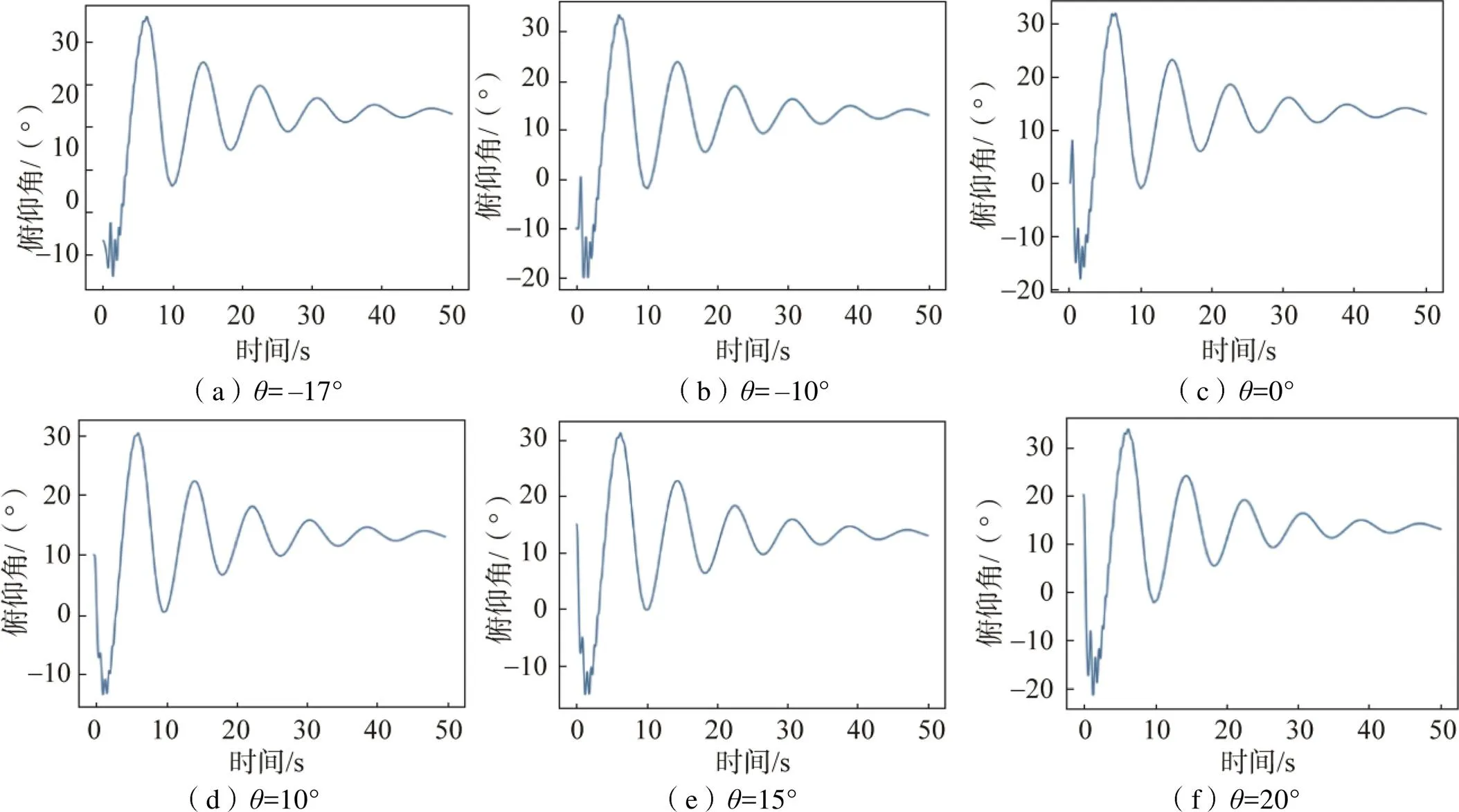
图9 不同摆角下放飞翼伞的俯仰角变化

2.3 拖曳过程仿真

由翼伞放飞的速度条件可初步令拖曳车加速至12 m/s，仿真分析不同加速度条件下，翼伞绕连接点的摆动情况如图10所示（注：由图2几何关系可知翼伞摆角与俯仰角相等）。由图中可以看出，加速度越大，拖曳初始翼伞摆动越剧烈，而且加速度越大或越小时翼伞稳定时间都会越长。通过比较图10所示各种运动情况，拖曳车在加速度为1～2 m/s2范围时，可以较快达到稳定且不产生剧烈摆动。

图10 拖曳车在不同加速度条件下翼伞绕连接点摆动情况

此外，为了得出拖曳车释放翼伞的最佳时机，还需研究拖曳车在此种运动模式下翼伞摆动的角速度变化规律。图11所示为汽车加速度在1 m/s2和2 m/s2情况下的摆动角速度变化，当汽车运动约25 s后，角速度均在–0.5～0.5 rad/s范围不断减小；结合翼伞摆角的变化看，如图10（b）～（c），此时摆角也大概稳定在5～15°范围内逐渐收敛；再结合表2可知此时达到放飞翼伞的初始条件。因此，为尽量减小拖曳距离以降低对跑道长度的要求，可以在拖曳车运动25 s后释放翼伞，即可实现翼伞的正常放飞。

图11 两种加速度下的拖曳过程翼伞摆动角速度变化

由此可以得出拖曳车最佳的运动模式为以1～2 m/s2的加速度加速至12 m/s，然后继续行驶至25 s左右后释放翼伞，如图12（a）和图12（c）所示。简单计算可得此过程的拖曳距离即所需的跑道长度大约为228～264 m，如图12（b）和图12（d）所示。

图12 两种加速度下的拖曳车的运动模式

3 结束语

目前，国内外对于动力翼伞的理论研究还处于起步阶段，主要集中在动力翼伞飞行过程的建模与仿真，对于动力翼伞起飞及降落过程的研究较少。本文以300 m2大型动力翼伞为研究对象，针对拖曳和起飞过程，建立了动力翼伞的纵向动力学模型，仿真分析了拖曳起飞过程翼伞的运动状态。通过控制变量分析了翼伞在不同初速度、角速度以及摆角下放飞的运动情况，得出了翼伞放飞的速度、角速度以及摆角条件。根据得到的条件求解了拖曳车在不同加速度运动时翼伞的摆动状态，获得了拖曳运动规律以及动力翼伞的起飞释放条件，研究内容可以为大型动力翼伞的设计与应用提供参考。

[1] 许望晶, 王立武, 滕海山, 等. 大型动力翼伞飞行器发展研究[J]. 航天返回与遥感, 2020, 41(4): 55-63.XU Wangjing, WANG Liwu, TENG Haishan, et al. Research on Development of Large Powered Parafoil Aircraft[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(4): 55-63. (in Chinese)

[2] KALRO V, ALIABADI S, GARRARD W, et al. Parallel Finite Element Simulation of Larger Ram-air Parachutes[J]. International Journal for Numerical Methods in Fluids, 1997, 24(12): 1353-1369.

[3] 张俊韬, 侯中喜. 动力翼伞系统纵向动力学建模研究[J]. 系统仿真学报, 2010, 22(11): 2541-2544. ZHANG Juntao, HOU Zhongxi. Research on Longitudinal Dynamic Modeling of Powered Parafoil System[J].Journal of System Simulation, 2010, 22(11): 2541-2544. (in Chinese)

[4] WARD M, CULPEPPER S, COSTELLO M. Parametric Study of Powered Parafoil Flight Dynamics[C]//AIAA Atmospheric Flight Mechanics Conference, August 13-16, 2012, Minneapolis, Minnesota, USA.

[5] 常冠清, 张泽, 仇海涛, 等. 翼伞系统动力学建模与仿真研究[J]. 导航与控制, 2016, 15(6): 33-40, 87. CHANG Guanqing, ZHANG Ze, QIU Haitao, et al. Dynamic Modeling and Simulation of Parafoil Aerial Delivery System[J].Navigation and Control, 2016, 15(6): 33-40, 87. (in Chinese)

[6] 蒋万松, 荣伟, 滕海山, 等. 翼伞—载荷系统多体动力学仿真分析[J]. 南京航空航天大学学报, 2016, 48(4): 474-480. JIANG Wansong, RONG Wei, TENG Haishan, et al. Multibody Dynamical Simulation Analysis for Parafoil-payload System[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(4): 474-480.

[7] ZHU Erlin, SUN Qinglin, TAN Panlong, et al. Modeling of Powered Parafoil Based on Kirchhoff Motion Equation[J]. Nonlinear Dynamics, 2015, 79(1): 617-629.

[8] 杨海鹏. 翼伞九自由度动力学建模与仿真[J]. 科技创新导报, 2017, 14(29): 7-9. YANG Haipeng. 9-DOF Dynamic Modeling and Simulation of Parafoil[J].Science and Technology Innovation Herald, 2017, 14(29): 7-9. (in Chinese)

[9] SLEGERS N. Comparison of Parafoil Dynamic Modes with Varying Payload Connections [C]// 24th AIAA Aerodynamic Decelerator Systems Technology Conference, June 5-9, 2017, Denver, Colorado, USA.

[10] ALTMANN H. Fluid-Structure Interaction Analysis of an Isolated Ram-Air Parafoil Cell[C]// AIAA Aviation 2019 Forum, June 17-21, 2019, Dallas, Texas, USA.

[11] 杨华, 宋磊, 王文剑, 等. 动力翼伞纵向四自由度动力学仿真[J]. 北京航空航天大学学报, 2014, 40(11): 1615-1622. YANG Hua, SONG Lei, WANG Wenjian, et al. 4-DOF Longitudinal Dynamic Simulation of Powered-Parafoil[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(11): 1615-1622. (in Chinese)

[12] 康鹤云. 动力翼伞飞行特性与控制研究[D]. 长沙: 国防科学技术大学, 2016. KANG Heyun. Research on Power Parafoil of Flight Characteristics and Control[D]. Changsha: National University of Defense Technology, 2016. (in Chinese)

[13] GORMAN C M, SLEGERS N J. Modeling of Parafoil-payload Relative Yawing Motion on Autonomous Parafoils[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 23-26, 2011, Dublin, Ireland.

[14] 胡文治. 翼伞空投系统的动力学与飞行控制仿真[D]. 南京: 南京航空航天大学, 2017. HU Wenzhi. Simulation on Flight Dynamics and Control of Parafoil Airdrop Systems[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017. (in Chinese)

[15] OCHI Y . Modeling and Simulation of Flight Dynamics of a Relative-roll-type Parafoil[C]// AIAA Scitech 2020 Forum, January 6-10, 2020, Orlando, FL, USA.

[16] 蒋万松, 荣伟, 滕海山, 等. 火箭助推器翼伞回收动力学仿真与试验分析[J]. 航天返回与遥感, 2017, 38(3): 13-23. JIANG Wansong, RONG Wei, TENG Haishan, et al. Dynamical Simulation and Test Analysis for Booster Recovery with Parafoil System[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 13-23. (in Chinese)

[17] 张青斌, 高峰, 郭锐, 等. 动力翼伞系统拟坐标形式的多体动力学建模[J]. 兵工学报, 2019, 40(9): 1935-1942. ZHANG Qingbin, GAO Feng, GUO Rui, et al. Multibody Dynamics Modeling of Powered Parafoil System Using Equations with Quasi-coordinates[J]. Acta Armamentarii, 2019, 40(9): 1935-1942. (in Chinese)

[18] MOHAMMAD M, AKITA U. Experiment Investigation on Aerodynamic Characteristics of a Paraglider Wing[J]. The Japan Society for Aeronautical and Space Sciences, 2006, 49(16): 9-17.

[19] 郭一鸣, 闫建国, 邢小军, 等. 变形翼伞回收系统的建模与分析[J]. 西北工业大学学报, 2020, 38(5): 952-958. GUO Yiming, YAN Jianguo, XING Xiaojun, et al. Modeling and Analysis of Deformed Parafoil Recovery System[J]. Journal of Northwestern Polytechnical University, 2020, 38(5): 952-958. (in Chinese)

[20] CHIN J, NIEHAUS J, GOODENOW D, et al. Flight Analysis of an Autonomously Navigated Experimental Lander for High Altitude Recovery[C]//AIAA SciTech Forum, January 4-8, 2016, San Diego, California, USA.

[21] NATHAN J S. Comparison of Parafoil Dynamic Modes with Varying Payload Connections[C]//24th AIAA Aerodynamic Decelerator Systems Technology Conference, June 5-9, 2017, Denver, Colorado, USA.

[22] 王立武, 许望晶, 刘涛, 等. 航天器翼伞精确回收技术发展及展望[J]. 航天返回与遥感, 2020, 41(4): 21-30. WANG Liwu, XU Wangjing, LIU Tao, et al. Development and Prospect of Parafoil Precise Recovery Technology for Spacecraft[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(4): 21-30. (in Chinese)

[23] LISSAMAN P, BROWN G. Apparent Mass Effects on Parafoil Dynamics[C]// AIAA Aerospace Design Conference, February 16-19, 1993,Irvine, CA, USA.

Research on Towing Take-Off Dynamics of Large Powered Parafoil

SU Haodong1,2TENG Haishan1,2LIU Yu1,2WU Zhuo1,2

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）（2 Laboratory of Aerospace Entry, Descent and Landing Technology, CASC, Beijing 100094, China）

Powered parafoil has the advantages of large payload, long endurance, high safety, high reliability and low cost. It has great development potential in military and civil fields. In this paper, aiming at the ground towing take-off process of power parafoil, according to the basic principle of Newtonian mechanics, a longitudinal dynamic model of power parafoil towing take-off is established to describe the motion state of powered parafoil towing, stability and release process. A simulation environment for the motion process of power parafoil is built. The motion state of the parafoil during towing and after releasing is simulated respectively. The stability of the parafoil in different motion parameters is compared through control variables. The release speed, angular velocity and angular conditions of the power parafoil are given. The reasonable motion mode of the ground towed vehicle and release time of the powered parafoil are obtained, which has certain guiding significance for the engineering application of the follow-up powered parafoil.

towing take-off; dynamics simulation; swing angle; towing vehicle movement; parafoil stability; powered parafoil

V212.13

A

1009-8518(2023)03-0009-12

10.3969/j.issn.1009-8518.2023.03.002

苏浩东，男，1996年生，2020年获南京航空航天大学机械工程专业学士学位，现于中国空间技术研究院攻读航空宇航科学与技术专业硕士学位。主要研究方向为航天器返回与着陆技术。E-mail：1256292577@qq.com。

2022-06-13

国家自然科学基金（11602018）

苏浩东, 滕海山, 刘宇, 等. 大型动力翼伞拖曳起飞动力学研究[J]. 航天返回与遥感, 2023, 44(3): 9-20.

SU Haodong,TENG Haishan,LIU Yu, et al. Research on Towing Take-Off Dynamics of Large Powered Parafoil[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(3): 9-20. (in Chinese)

（编辑：陈艳霞）