降落伞临界开伞速度研究

隋蓉 张文博

降落伞临界开伞速度研究

隋蓉 张文博

（北京空间机电研究所，北京 100094）

为了解航天器用降落伞的使用边界，计算降落伞临界开伞速度，文章基于充气体积理论推导了临界开伞速度的理论计算公式，讨论了影响临界开伞速度的因素。研究结果表明，降落伞临界开伞速度与大气密度、织物透气量、伞衣顶部结构透气量成反比；通过伞绳长度增加，影响伞衣充气进气口尺寸提高降落伞的临界开伞速度；降落伞临界开伞速度与伞衣尺寸的关系和降落伞充气过程底边尺寸有关；在降落伞底边尺寸大于某一临界值时，降落伞临界开伞速度与伞衣尺寸成正比；在降落伞底边尺寸小于某一临界值时，降落伞临界开伞速度与伞衣尺寸成反比。文章基于降落伞临界开伞速度与伞衣充气外形尺寸相关这一理论，提出计算收口状态下降落伞的简化充气外形尺寸方法，计算结果与流固耦合仿真结果一致。文章的研究结论可用于评估降落伞的开伞条件，为降落伞设计、应用提供参考。

降落伞 充气 临界开伞速度 返回着陆

0 引言

降落伞是一种依靠自身展开的形状与结构来减速的柔性减速装置，在“嫦娥五号”探测器、火星探测等航天器的进入、减速过程中发挥着重要的作用。降落伞工作过程十分复杂，其中降落伞的开伞充气阶段又是降落伞工作过程中最为重要也是物理过程最为复杂的一个阶段，影响降落伞任务及再入返回过程的成败。降落伞的充气过程是降落伞研究人员最为关注的一个过程，表征降落伞充气过程的指标一般有充气时间[1]、充气阻力面积变化过程[2]、充气距离[3]等，研究方法一般分为流固耦合仿真计算[4-6]、动量方程法[7]、试验法[8-9]三大类，降落伞设计参数和使用环境参数[10-11]均会对降落伞充气过程表征指标产生影响。已有研究结果表明，降落伞的充气过程与伞衣底边形状、速度及伞衣透气量等因素密切相关且具有一定的随机性[12]。在降落伞的风洞试验中发现，只有处于一定的边界条件内，降落伞才具备充满的条件[13]。当降落伞的开伞速度增大到一定程度时，降落伞将成“乌贼”状态，不能充满，且随着速度的增大，降落伞的充气体积会逐渐变小。定义降落伞能够充满的最大来流速度为降落伞临界开伞速度[14]。临界开伞速度与进入伞衣的气体量及流出伞衣的气体量有关，当进入伞衣的气体量大于流出伞衣的气体量时，降落伞可以充满，否则降落伞呈现“乌贼”状态。

针对降落伞临界开伞速度的研究，国内还未见相关的研究报道，国外有研究人员在试验中发现降落伞临界开伞速度与降落伞伞衣尺寸成反比，提出了临界开伞速度与降落伞流入、流出的气体量有关[15]，并定性地提出了可能影响降落伞临界开伞速度的因素有伞衣尺寸、大气密度等。在降落伞临界开伞速度的理论数值计算领域尚未有相关的研究，降落伞临界开伞速度的影响因素的定量研究尚处于空白状态，随着航天技术的不断发展，面对载人航天、深空探测等重大回收任务中越来越复杂、严酷的开伞条件，降落伞的使用条件越来越严苛。为了解降落伞的使用边界，提高降落伞系统的可靠性，有必要对降落伞临界开伞速度的计算方法及影响因素开展研究。

本文从推导降落伞临界开伞速度的理论计算公式入手，从降落伞设计参数和大气环境参数两类因素展开，讨论分析各因素对降落伞临界开伞速度的影响。通过研究降落伞的临界开伞速度的影响因素，可以有针对性的对降落伞的使用环境在设计阶段就开展降落伞的优化设计，通过调整降落伞参数的方式提高降落伞的临界开伞速度，提升降落伞设计水平。

1 临界开伞速度的计算

为了计算临界开伞速度，假设降落伞的充气状态为灯泡状，伞衣外形近似为半球型与圆锥台的组合体，如图1所示。降落伞充气扩张过程发生的条件为气体流入伞衣的体积大于气体流出伞衣的体积。假设在不可压缩流的条件下，不考虑气体密度的变化，伞衣内体积的变化可表示为[14]

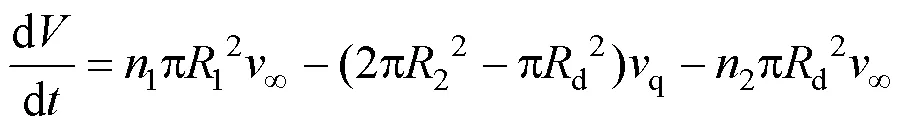
根据降落伞织物透气量理论有

经试验测量典型织物伞衣压差系数与织物透气量曲线如图2所示[13]，压差系数随流出伞衣的气体速度增大而减小，小透气量织物的压差系数为1.6，压差系数随着织物透气量的增大而减小。

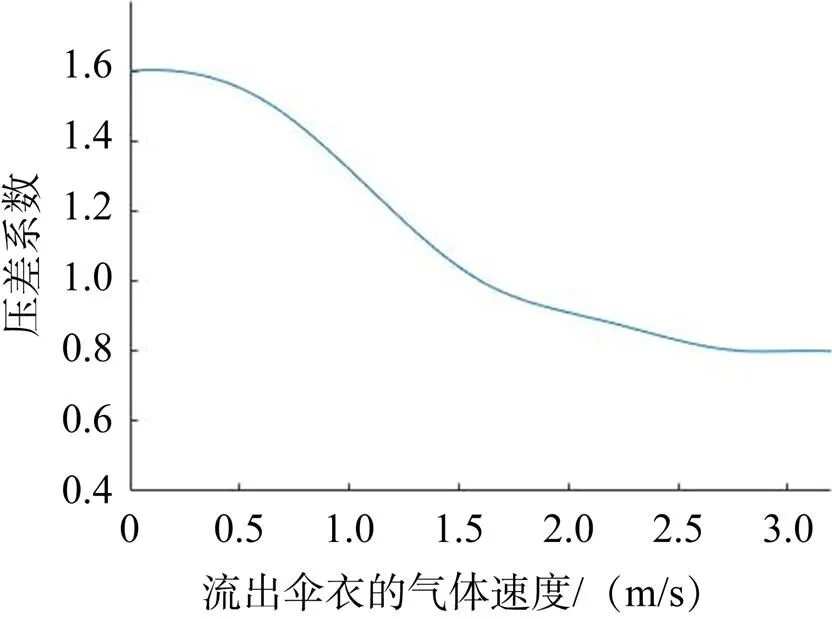
图2 压差系数与透气量的关系曲线

图3 不同织物透气量拟合曲线

2 临界开伞速度影响因素研究

从式（1）中可得出，影响临界开伞速度的因素与进气口参数、伞衣局部结构透气量参数、伞衣织物透气量参数以及影响以上参数的因素有关。本节将对影响临界开伞速度的各因素展开讨论。

2.1 临界开伞速度与织物透气量之间的关系

通过试验测得几种常用降落伞伞衣织物材料透气量，由式（3）拟合不同织物的、值，获得拟合曲线如图3所示，拟合参数见表1，拟合优度接近1，拟合效果良好。相同压差条件下，流出伞衣的气体速度越大，代表织物的透气量越大。

表1 不同织物在不同压差条件下的透气量

Tab.1 The permeability of different fabrics under different pressure differences

根据式（2），仅织物透气量不同，其余参数保持一致，计算不同织物临界开伞速度如图4所示。结合图3，透气量最大的材料518防灼白色锦丝绸，其临界开伞速度最小，k58326-3防灼红色锦丝格子绸次之。而k59321防灼白色锦丝绸与544防灼轧光红色锦丝格子绸的透气量较小，在本文方法下计算得到的临界开伞速度已超出了亚声速的范围，由于在超声速条件下，表征织物透气量的欧根公式即式（3）已不再适用，因此本文针对超声速条件下的临界开伞速度暂不做讨论。由图4可知，降落伞临界开伞速度与织物透气量成反比，织物透气量越大，临界开伞速度越低，针对开伞条件恶劣的降落伞设计，从优化降落伞开伞性能的角度，在设计中可以考虑采用织物透气量小的伞衣材料。

图4 不同透气量伞衣织物降落伞临界开伞速度比较

2.2 临界开伞速度与大气密度的关系

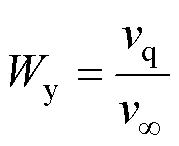
结合式（2），得到织物有效透气量

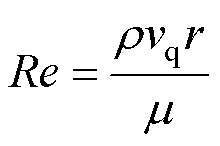
2.3 临界开伞速度与伞衣顶部结构透气量的关系

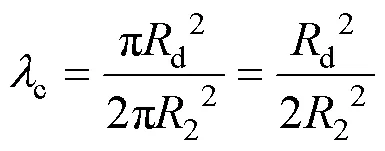
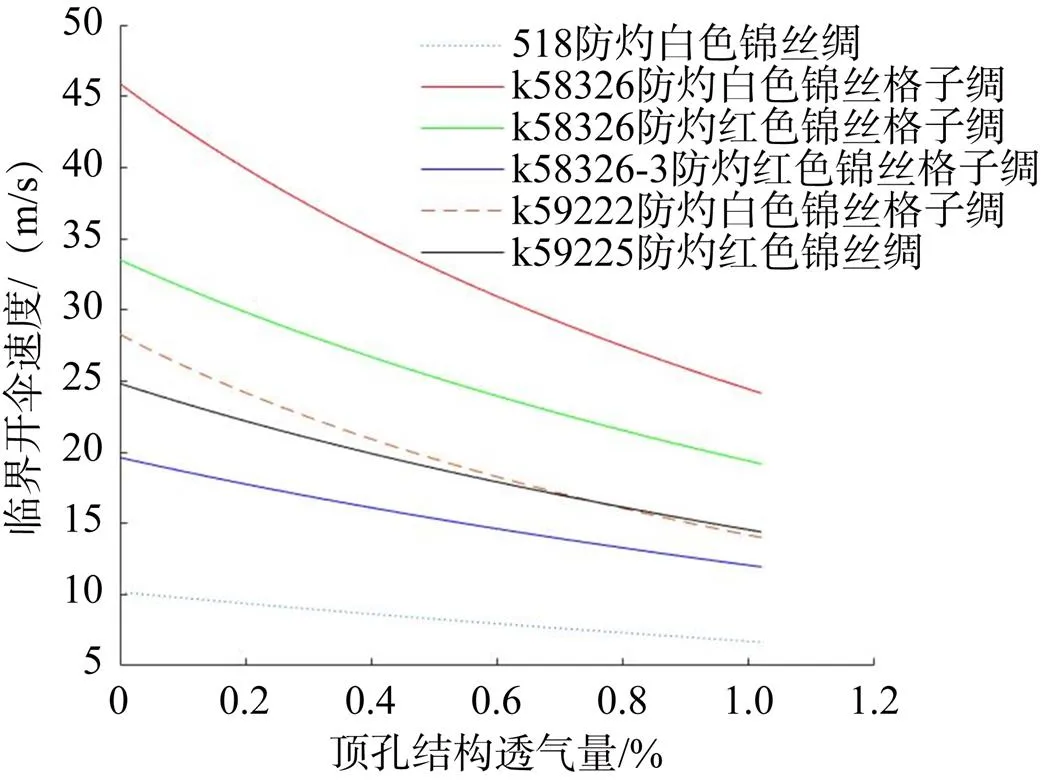
图5 临界开伞速度随伞衣顶部结构透气量变化曲线

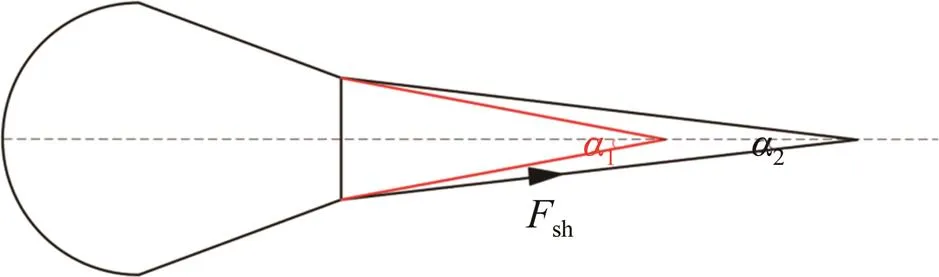
图6 降落伞伞绳长度变化引起降落伞伞衣底边受力变化示意

Fig.6 Schematic diagram of the force change on the bottom edge of the parachute caused by the change in the length of parachute lines

图7 降落伞临界开伞速度随R2/R1的变化

2.4 伞绳长度对临界开伞速度的影响

降落伞伞绳长度变化引起降落伞伞衣底边受力变化如图6所示，伞绳力为sh。短伞绳条件下，伞绳与降落伞轴线夹角1；长伞绳条件下，伞绳与降落伞轴线夹角2。1＞2，伞绳力径向分力shsin1＞shsin2，当伞绳长度增加，伞绳力径向分力减小，伞衣底边向外扩张，会增大降落伞的进气口面积，有利于提高降落伞的临界开伞速度。

2.5 临界开伞速度与伞衣几何外形的关系

根据临界开伞速度计算公式，临界开伞速度与伞衣几何外形尺寸1、2密切相关。降落伞顶部直径与口部直径比为2/1，仅2/1取值不同，其余参数保持一致，结合公式（1）～（3），计算降落伞临界开伞速度随2/1的变化如图7所示，当2/1增大，降落伞临界开伞速度降低。

2.6 临界开伞速度与伞衣尺寸的关系

由图1可知，根据几何相似性，有

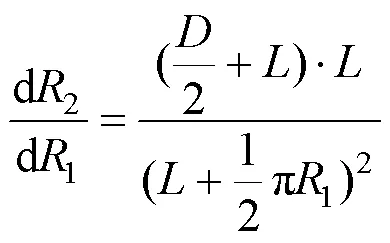
记

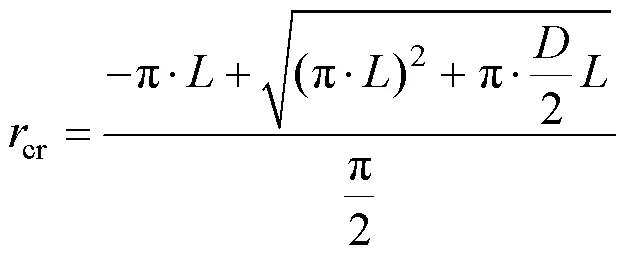
3 临界开伞速度理论的应用——收口状态降落伞充气外形计算

3.1 计算方法

图8 典型收口状态降落伞的充气过程

3.2 仿真对比验证

以猎户座降落伞收口状态为研究对象计算临界开伞速度随2/1的变化，采用流固耦合仿真计算结果作为对比验证，降落伞参数与计算条件参考文献[18-20]，文献[18-20]中给出计算的降落伞顶部结构透气量为6.89%，采用本文2.4节计算方法，结合式（1）～（3），计算不同2/1条件下对应的降落伞临界开伞速度，降落伞临界开伞速度与2/1的对应关系如图9所示。文献[18-20]计算来流速度为18m/s，按照本文降落伞临界开伞速度理论的计算方法，当临界开伞速度为18m/s时，对应的2/1≈2.57。流固耦合仿真计算的降落伞外形图如图10所示。用图片处理软件测量图10中1与2的尺寸，2/1≈2.55，本文降落伞临界开伞速度理论的计算方法获得的降落伞外形与流固耦合仿真外形结果具有一致性。

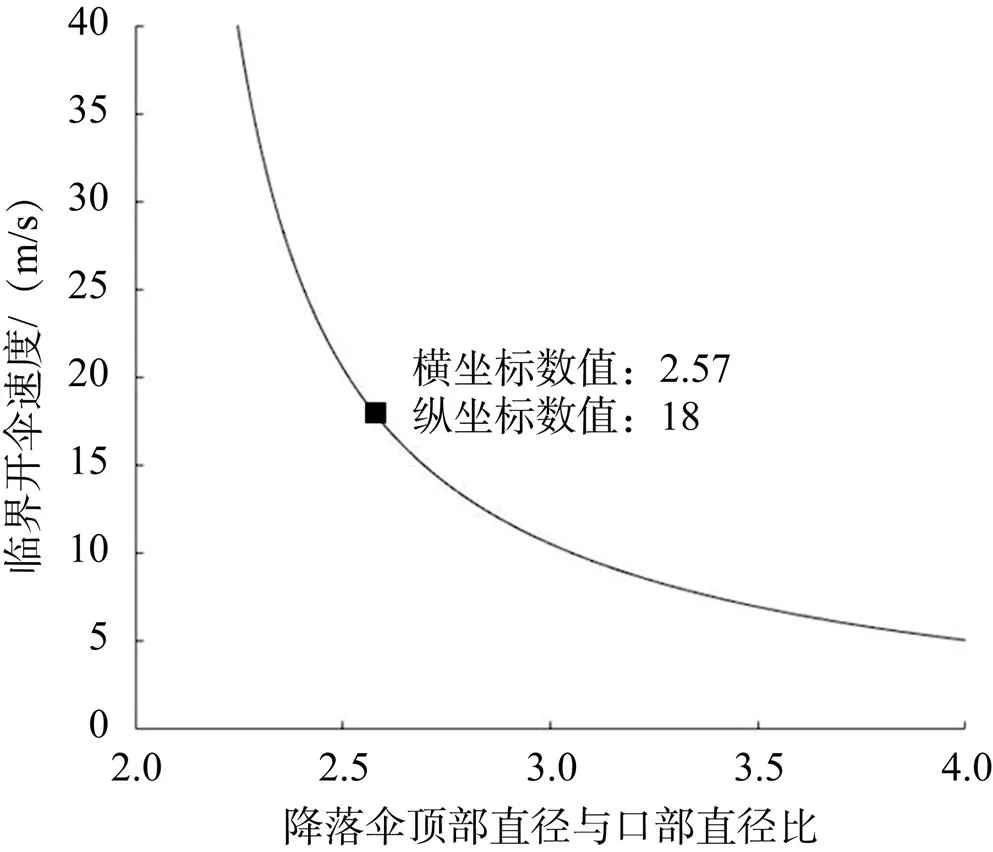
图9 收口状态降落伞临界开伞速度随R2/R1的变化

图10 收口状态降落伞流固耦合仿真计算充气外形

4 结束语

文章推导了临界开伞速度的理论计算公式，结合亚音速条件下的欧根公式讨论了影响临界开伞速度的因素，并对各影响因素开展了定量、定性分析，填补了国内关于降落伞临界开伞速度领域研究的空白，得出了以下结论：

1）在亚声速条件下，临界开伞速度与织物透气量、伞衣顶部结构透气量成反比，在开伞条件较为苛刻的降落伞设计中，可考虑采用低透气量伞衣材料、减小伞衣顶部结构透气量来改善降落伞的开伞性能；

2）降落伞临界开伞速度与大气密度成反比，在低海拔地区降落伞临界开伞速度小于高海拔地区，这是由于密度降低会导致织物有效透气量增加，使临界开伞速度增加；

3）通过定性分析，伞绳长度增加会通过影响伞衣充气进气口尺寸，增大降落伞的临界开伞速度；

4）降落伞临界开伞速度与伞衣充气外形尺寸相关，基于这一理论可计算收口状态降落伞的简化充气外形尺寸，计算结果与流固耦合仿真结果具有一致性；

5）降落伞临界开伞速度与伞衣尺寸的关系和降落伞充气外形尺寸1有关，在1大于某一临界值时，降落伞临界开伞速度与伞衣尺寸成正比，在1小于某一临界值时，降落伞临界开伞速度与伞衣尺寸成反比。

降落伞临界开伞速度受多因素影响，在工程应用中需要对各因素综合考虑。由于临界开伞速度的实际验证试验实施存在困难，本文的理论尚未开展试验验证，后续可通过风洞试验、空投试验对该理论做进一步的验证和探索。本文只针对亚声速范围内的降落伞开伞情况进行了讨论，后续可开展超音速范围内降落伞开伞理论的研究工作。

[1] HENG H, CHEN C, LIU X, et al. Numerical Study of Parachute Inflation Process Based on Smoothed Particle Hydrodynamics Fluid Structure Interaction Method[J]. Journal of Industrial Textiles, 2018, 47(6): 1038-1059.

[2] 高树义, 余莉. 环帆伞收口比对开伞性能的影响[J]. 中国空间科学技术, 2014, 34(1): 63-70. GAO Shuyi, YU Li. Influence of Reefing Ratio on Inflation Performance of Ringsail Parachute[J]. Chinese Space Science and Technology, 2014, 34(1): 63-70. (in Chinese)

[3] 荣伟, 包进进. 火星大气对降落伞充气性能影响的初步探讨[J]. 航天返回与遥感, 2017, 38(4): 1-7. RONG Wei, BAO Jinjin. The Primary Studies on the Effect of Martian Atmosphere on Parachute Inflation Performances[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(4): 1-7. (in Chinese)

[4] TUTT B A, TAYLOR A P. The Use of Ls-dyna to Simulate the Inflation of a Parachute Canopy[C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, May 23-26, 2005, Munich, Germany. AIAA, 2005: 2005-1608-1-2005-1608-9.

[5] 高兴龙, 唐乾刚, 张青斌, 等. 开缝伞充气过程流固耦合数值研究[J]. 航空学报, 2013, 34(10): 2265-2276. GAO Xinglong, TANG Qiangang, ZHANG Qingbin, et al. Numerical Study on Fluid-structure Interaction of Slot-parachute’s Inflation Process[J]. Acta Aeronautica Et Astronautica Sinica, 2013, 34(10): 2265-2276. (in Chinese)

[6] 陈晨, 郭琪磊. 一种基于任意拉格朗日-欧拉方法的降落伞充气展开数值模型[J]. 科学技术与工程, 2021, 21(2): 801-807. CHEN Chen, GUO Qilei. A Numerical Model of Parachute Deployment Inflation Process Based on Arbitrary Lagrange-Euler Method[J]. Science Technology and Engineering, 2021, 21(2): 801-807. (in Chinese)

[7] 郭叔伟, 董杨彪, 王海涛, 等. 降落伞充气环境对充气性能的影响[J]. 中国空间科学技术, 2008, 28(6): 45-51. GUO Shuwei, DONG Yangbiao, WANG Haitao, et al. Influence of Inflation Conditions Parachute Inflation[J]. Chinese Space Science and Technology, 2008, 28(6): 45-51. (in Chinese)

[8] 徐宏, 曹义华. 降落伞典型开伞过程的试验研究[J]. 飞行力学, 2012, 30(1): 74-78. XU Hong, CAO Yihua. Experimental Investigation in Typical Parachute Opening Process[J]. Flight Dynamics, 2012, 30(1): 74-78. (in Chinese)

[9] 王国辉, 牟宇, 张然, 等. 超声速降落伞工程应用的关键技术研究进展[J]. 宇航总体技术, 2022, 6(2): 1-16. WANG Guohui, MOU Yu, ZHANG Ran, et al. Recent Progress in Key Technology of Supersonic Parachute Application in Engineering Design[J]. Astronautical Systems Engineering Technology, 2022, 6(2): 1-16. (in Chinese)

[10] 余莉, 明晓, 胡斌. 降落伞开伞过程的试验研究[J]. 南京航空航天大学学报, 2006, 38(2): 176-180. YU Li, MING Xiao, HU Bin. Experimental Investigation in Parachute Opening Process[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(2): 176-180. (in Chinese)

[11] 荣伟, 陈旭, 陈国良. 大气密度对降落伞充气性能的影响[J]. 航天返回与遥感, 2006, 27(3): 11-16. RONG Wei, CHEN Xu, CHEN Guoliang. The Effect of Atmospheric Density on Parachute Inflation Performances[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(3): 11-16. (in Chinese)

[12] 荣伟, 陈旭, 陈国良. 低密度大气中降落伞开伞动载的研究[J]. 航天返回与遥感, 2006, 27(4): 7-11. RONG Wei, CHEN Xu, CHEN Guoliang. The Study of the Parachute Opening Load in Low Atmospheric Density[J]. Spacecraft Recovery & Remote Sensing, 2006, 27(4): 7-11. (in Chinese)

[13] KENNETH E. Parachute Critical Opening Velocity[J]. Journal of Aircraft, 1971, 8(8): 674-677.

[14] 王利荣. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997. WANG Lirong. Parachute Theory and Application[M]. Beijing: China Astronautics Press, 1997. (in Chinese)

[15] LUDTKE W P. Notes on the Cause of Parachute Critical Velocity: 92-01253-DTIC[R]. 1991.

[16] 程涵, 余莉, 夏刚. 降落伞充气过程中“瓶颈”效应[J]. 国防科技大学学报, 2013, 35(1): 48-52. CHENG Han, YU Li, XIA Gang. A Study on "Bottleneck" Phenomenon during Parachute Inflation[J]. Journal of National University of Defense Technology, 2013, 35(1): 48-52. (in Chinese)

[17] 张红英, 刘卫华, 秦福德, 等. 降落伞充气过程中伞衣外形及流场变化研究[J]. 空气动力学学报, 2011, 29(3): 288-294. ZHANG Hongying, LIU Weihua, QIN Fude, et al. Study on the Canopy Shape and the Flow Field during Parachute Inflation Process[J]. Acta Aerodynamica Sinica, 2011, 29(3): 288-294. (in Chinese)

[18] TAKIZAWA K, FRITZE M, MONTES D, et al. Fluid – Structure Interaction Modeling of Ringsail Parachutes with Disreefing and Modified Geometric Porosity[J]. Comput Mech, 2012(50): 835-854.

[19] BOBEN J J. Fluid Structure Interaction Modeling of Modied-porosity Parachutes and Parachute Clusters[D]. Houston: Rice University, 2013.

[20] TAKIZAWA K, SPIELMAN T, TEZDUYAR T E. Space – Time Fsi Modeling and Dynamical Analysis of Spacecraft Parachutes and Parachute Clusters[J]. Comput Mech, 2011, 48(3): 345-364.

The Research on the Critical Velocity of Parachute Opening

SUI Rong ZHANG Wenbo

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

In order to understand the application boundary of parachute and calculate the critical velocity of parachute opening, the theoretical calculation formula of parachute critical velocity is derived, and the factors affecting the critical velocity of parachute opening are discussed. The results show that the critical opening velocity of parachute opening is inversely proportional to the air density, fabric permeability and crown parachute poriosity. The increase of parachute suspension line and the gores of parachute will increase the critical velocity by affecting the size of parachute inflation inlet. When the bottom size of parachute is larger than a critical value, the critical velocity of parachute opening is proportional to the size of parachute. When the bottom size of parachute is less than a critical value, the critical velocity of parachute is inversely proportional to the size of parachute. The critical velocity of parachute opening is related to the dimension of parachute. Based on this theory, the simplified inflatable dimension of reefing parachute is proposed, and the calculated results are consistent with the FSI simulation results. The research work in this paper can provide reference for parachute design and application.

parachute; inflation; critical velocity; return and landing

V244.21

A

1009-8518(2023)03-0001-08

10.3969/j.issn.1009-8518.2023.03.001

隋蓉，女，1993年生。2018年获中国空间技术研究院飞行器设计专业硕士学位，工程师。主要研究方向是航天器减速系统设计。E-mail：suirong2011@qq.com。

2022-06-20

工业和信息化部重点实验室开放基金（KLAECLS-E-202004）

隋蓉, 张文博. 降落伞临界开伞速度研究[J]. 航天返回与遥感, 2023, 44(3): 1-8.

SUI Rong, ZHANG Wenbo. The Research on the Critical Velocity of Parachute Opening[J]. Spacecraft Recovery & Remote Sensing, 2023, 44(3): 1-8. (in Chinese)

（编辑：庞冰）