非等温树脂传递模塑成型仿真建模及应用

2023-06-15高胜晖段跃新

航空材料学报 2023年3期

赵亮, 高胜晖*, 段跃新

（1.中国航发北京航空材料研究院，北京 100095；2.北京航空航天大学，北京 100191）

树脂基复合材料有着良好的力学性能、质量轻、耐腐蚀等特点，在航空、交通、电子电力等领域应用广泛，其中一种高效的成型技术是树脂传递模塑成型（ resin transfer molding， RTM）。采用RTM 工艺模拟仿真，可以有效的预测树脂填充时间，优化注胶口位置和溢料口位置，避免干斑缺陷，从而改善传统试错的工艺验证方式，有效缩短工艺设计时间，节约成本。在实际生产过程中，非等温RTM 过程是更为接近真实生产过程的物理描述。相比等温RTM 的仿真建模，非等温RTM 需要同时考虑温度和流场的耦合计算，对算法的可靠性和收敛性均提出了较高的要求。国外商业化软件如法国的PAM-RTM、比利时的RTM-Worx 等均实现了非等温RTM 工艺的仿真求解，在国内企业得到广泛应用。长期以来国内针对RTM 仿真求解器的研发主要以等温求解为主，针对非等温过程的热流耦合求解仍然处于基础研究阶段，目前国内尚缺少成熟的针对工程应用的非等温RTM 工艺仿真模型，在实际生产过程中长期依赖国外商业化模型。随着我国对基础工业仿真重视程度的进一步提升，工艺制造仿真作为基础工业仿真的组成部分，也受到广泛的关注和重视。

RTM 工艺的充模过程是一种典型的非定常流动现象，对于该过程的模拟仿真国内外学者分别采用有限元、有限元控制体积法、有限差分法等进行了研究。有限元方法可以用来模拟树脂充模的工艺过程,但传统有限元方法固有的特点使得求解过程较繁琐，内存消耗较大，计算速度较慢，且在追踪流动前锋上存在一定不足[1]。达西定律适用于多孔介质中低速稳态流动的描述，当采用达西定律描述树脂在纤维中的流动时，需要假定在短时间内树脂的流动是一种稳态流动，然后可采用有限元方法求解，最终得到树脂流动的速度和压力分布[2-4]。

控制体/有限元法综合了有限体积方法（FVM）和有限元方法（FEM）的优点，逐渐成为主流的RTM 仿真工艺数值算法。Bruschke 等[5]采用CV/FEM 方法模拟了树脂在渗透率各异的纤维铺层中的等温充模过程，经过实验验证，在充填时间和流动前锋方面数值结果与实验结果吻合较好。Bruschke 等较早考虑了RTM 工艺中的非等温的现象，采用CV/FEM 模拟了热传导和固化反应等对工艺过程的影响。区别于传统的控制体/有限元方法，Trochu 等[6]和赵亮等[7]采用了类CV/FEM方法，将网格单元看作一个控制单元，将压力场结果存储到单元的重心位置，通过有限元方法得到了充模过程中的压力值，通过比较，与实验结果吻合较好。北京航空材料研究院2000 年与北京航空航天大学梁志勇等[8]采用CV/FEM 方法合作开发了具备自主知识产权的二维RTM 工艺仿真软件BHRTM，该软件可在二维空间迅速简便实现RTM 工艺几何创建和网格的自动划分，在后处理结果展示中可对树脂流动和压力场演化过程进行伪三维显示。尹明仁等[9]基于CV/FEM 方法开发了模拟软件平台BHRTM-2，该平台可实现充模过程的可视化显示，对工艺设计中可能出现的干斑等问题起到了较好的指导作用。施飞[10]基于CV/FEM 方法实现了在非结构四面体网格中RTM 工艺的数值模拟，包括等温和非等温工艺过程，模拟结果与实验结果吻合较好。

有限差分法对控制方程直接差分化，程序实现相对较为简单，最有代表性的方法是贴体坐标法[11-12]，该方法首先需要对网格进行雅克比空间变换，得到规则形状的计算域,随后采用有限差分法求解。Coulter 等[13]根据达西定律,采用有限差分法模拟了树脂在充模过程的非等温流动,考虑了充模过程中树脂因热传递、固化反应等引起的温度变化最终对充模过程的影响。Friedrichs 等[14]和施飞等[15]采用有限差分方法中的贴体坐标法模拟了树脂流过形接头的情形,考虑了不同部件间网格并不一定完全一致的情形，最终得到了不同时刻的树脂流动前沿曲线以及最终的压力分布情况。李海晨等[16]采用有限差分算法模拟了树脂传递模塑成型工艺的等温过程，得到了充模过程中前锋形状的变化和不同时刻下压力场的分布情况，仿真结果与其他程序仿真结果吻合较好。

控制体有限元方法相比于传统的有限元方法和有限体积方法具有编程简单的优势，同时相对于有限差分和边界元等方法具有更好的守恒特性，适用于RTM 工艺中树脂流动过程的仿真建模。从仿真经验来讲，在相同数值精度下，六面体网格相比于四面体网格计算结果要更精确。然而，在RTM工艺仿真中，将控制体有限元方法应用于六面体单元的仿真模型并不多见，本工作将基于六面体网格单元构建RTM 工艺的数值模型。

1 模型

1.1 物理模型

在真实的 RTM 工艺中，树脂在流动过程中与纤维之间不断发生热交换，使得树脂本身的温度、黏度、固化度不断变化。固化反应的效应又反过来影响树脂的温度和黏度，各因素之间相互影响，最终对树脂的流动模式产生改变，建立非等温模型是目前数值刻画这些因素的主要方法。

（1） Darcy 方程

在树脂传递模塑成型工艺中，由于树脂充填速度一般很小，流动雷诺数较低，树脂在多孔介质中的流动服从Darcy 定律，当假定树脂黏度在短时间内不发生变化时，树脂流动速度与压力梯度成正比，Darcy 方程为：

式中：V是 Darcy 速率；[K] 是纤维增强体渗透率的二阶张量；μ是树脂黏度； ∇P是压力梯度。

在非等温 RTM 模型中，树脂的流动与等温情况有所差异，却依然遵循 Darcy 定律，但树脂黏度μ不再是一个常数，而是随着温度和固化度变化不断变化的量。刻画树脂流变性能的模型有很多，如一阶等温模型、凝胶模型、双阿累尼乌斯黏度模型等。

（2）连续性方程

连续性方程是流动的守恒方程，在流体微小体积单元内，质量随时间的变化率应等于在这段时间内流入该微小体积的净质量

式中：ρ是树脂密度；t是时间；ϕ是纤维的孔隙率。由于树脂流动速度较低，黏度较大，在短时间内可假定树脂的密度不发生变化，即 ∂ρ/∂t =0。连续性方程可简化为：

数值求解中，速度和压力的边界条件为：（1）在壁面处，速度为无穿透边界条件，压力取零法向梯度边界条件；（2）注胶口处，可根据输入的工艺条件选择恒压注射和恒流注射，若采用恒压注射，p = p0，p0为注射压力；如果采用恒流注射，V = V0，V0是注射速度。

（3）能量守恒方程

在 RTM 数值仿真的非等温模型中，温度随时间和空间不断变化，变化的温度影响了树脂的黏度和固化度，而固化反应的发生又反过来影响了树脂的温度和黏度，黏度的变化通过影响流动速度也必然引起温度和固化度的变化，这三个量的综合作用下最终影响了树脂的流动模式。在此过程中，影响因素众多，需建立相应的模型和方程来定量刻画诸因素的影响，首先考虑关于温度的能量方程。

在模具内，当假定纤维温度与树脂的温度相同时，即Tf= Tr= T，该假设忽略了树脂与纤维之间的热传递，关于树脂的能量方程和纤维的能量方程可不必分开求解，而是共同遵循平衡模型下的能量方程：

式中：等式左边第一项是树脂和纤维增强体温度随时间的变化率，偏导数前的系数是树脂和纤维的综合热效应；第二项是树脂随充模过程引起的热对流效应；等式右边第一项是热扩散项，表征由不同方向上温度的不均匀性引起的热传导，其中krf代表xyz三个方向上的热传导系数；右边最后一项是固化热源项，表征因固化反应放热带来的热量的产生。

（4）固化动力学方程

在 RTM 成型工艺中，当达到一定温度时，树脂分子间便会发生聚合，即树脂的固化反应。固化反应使得树脂流动性变差，黏度增加，但固化反应中释放的热量又促使树脂黏度变小。树脂固化反应的控制方程为：

式中：α为树脂固化度，取值范围为0～1；f（α，Tr）为树脂的固化反应速率，由固化反应的模型刻画，在数值求解时，采用了与能量方程中固化热源项类似的处理方式，对该项进行了线化处理。

（5）流变模型

在RTM 成型工艺中，由于温度在空间和时间尺度上不断变化，树脂的黏度也在不断发生变化，黏度的变化最终对填充结果有着较大的改变。树脂黏度模型主要包括理论模型、经验模型和半经验模型，在数值求解中引入黏度模型可用来定量刻画黏度随温度时间等的变化。黏度模型也常常表述为流变模型，其中经验/半经验模型因其经济实用性在 RTM 工艺具有更广泛的应用。经验模型包括工程黏度模型、双阿累尼乌斯黏度模型、（williamslandel-ferry， WLF）方程等[17-18]。其中双阿累尼乌斯模型方程是适用性较广的经验流变模型，该模型是在研究环氧树脂体系黏度变化规律的基础上提出的半经验公式，需假设树脂体系的固化反应为一级反应或某些总体为非一级动力学反应的树脂体系；工程黏度模型是另一种适用较广的经验方程，其基本原理是树脂体系物理和化学反应相互作用最终导致了树脂固化过程中黏度的变化；WLF 方程适用于研究热固性树脂体系的黏度变化。

1.2 计算模型

控制体/有限元方法并不限定网格类型，二维中的多边形，三维中的多面体也均适用。如图1 所示，以规则的四边形单元为例，控制体是由包含该节点的四边形单元各边的中点与四边形重心的连线围成，每个控制体归属中心节点所有，数值计算的结果也均存储于节点处。如图1 所示，Ni,j是阴影构成的控制的中心节点，Q1～Q8 是构成该控制体的小面。在RTM 工艺中，树脂的流动遵循物质守恒定律和达西定律，根据这两个方程可求得关于压力的拉普拉斯方程。CV/FEM 方法将压力定义在每个节点上，在每个小控制体上对压力方程进行离散可得到一些列的代数方程，求解后便可得到计算域内压力的分布，再结合达西定律，就可求得树脂的流动情况即树脂速度场的分布情况。

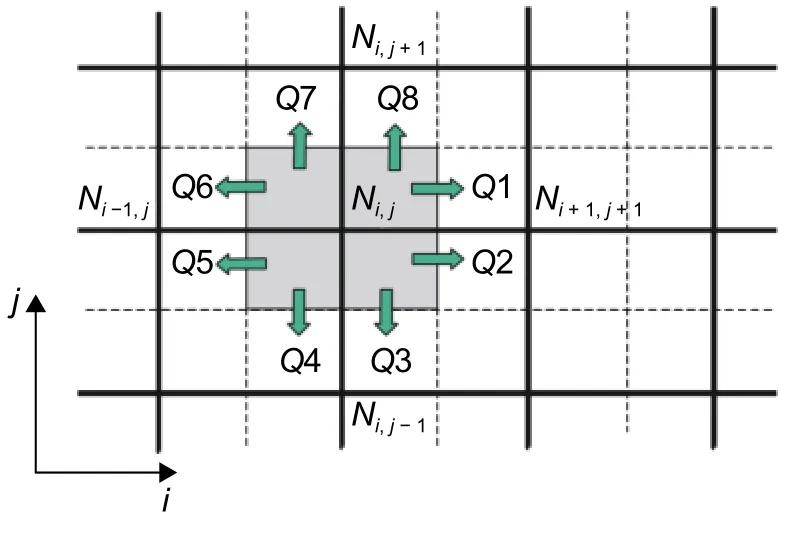
图1 CV/FEM 单元示意图Fig. 1 Diagram of the CV/FEM cell

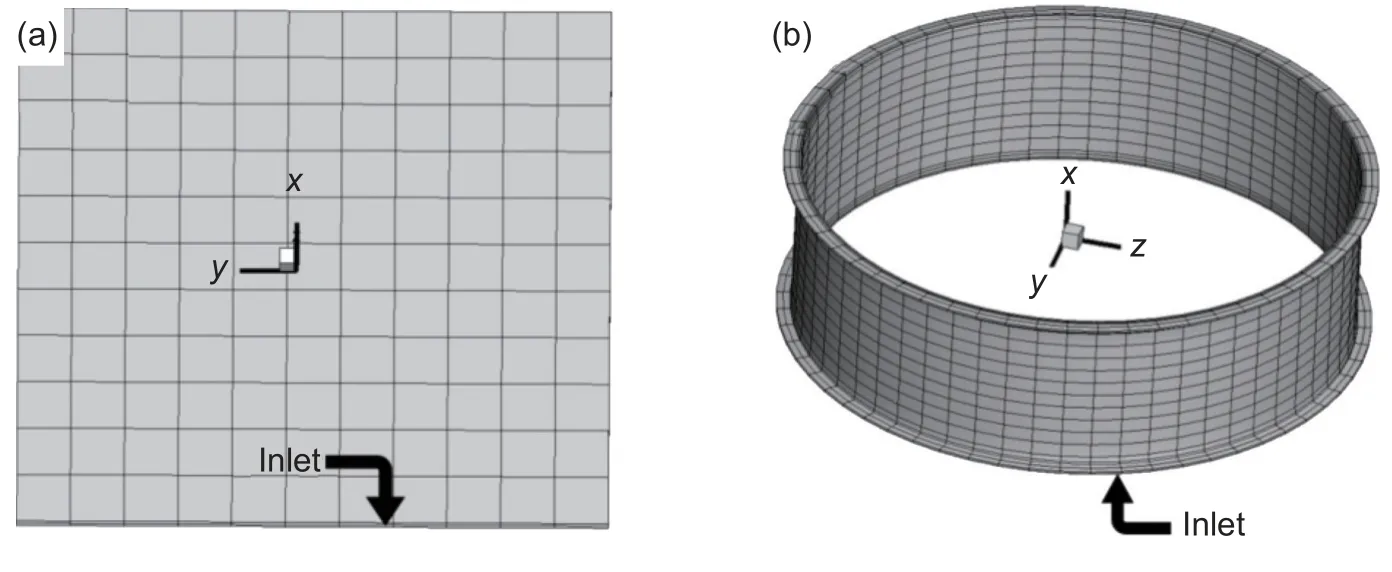
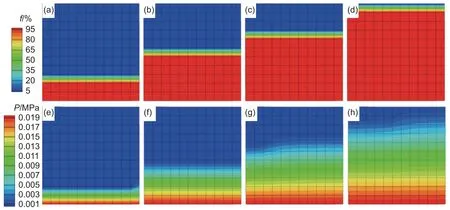
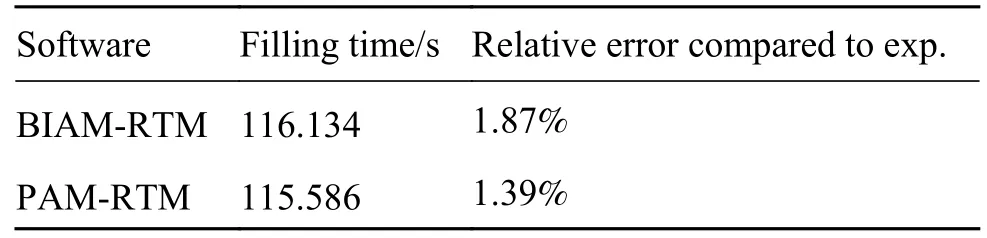
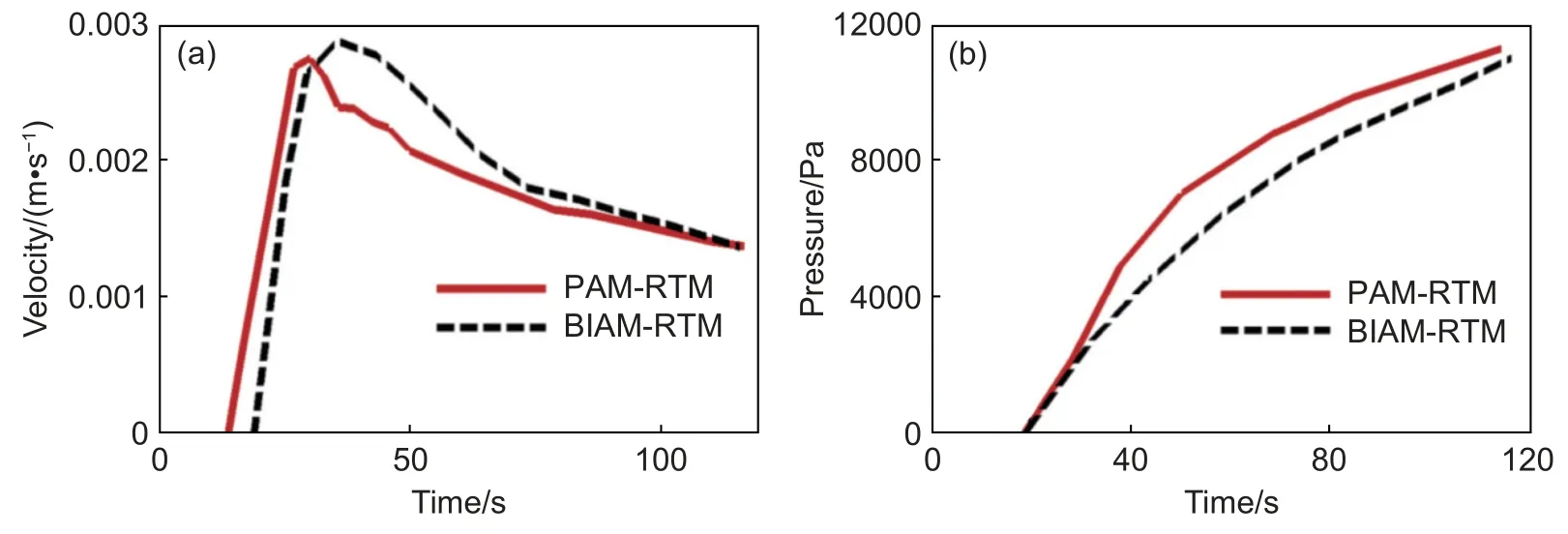
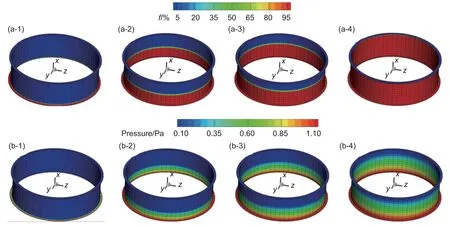
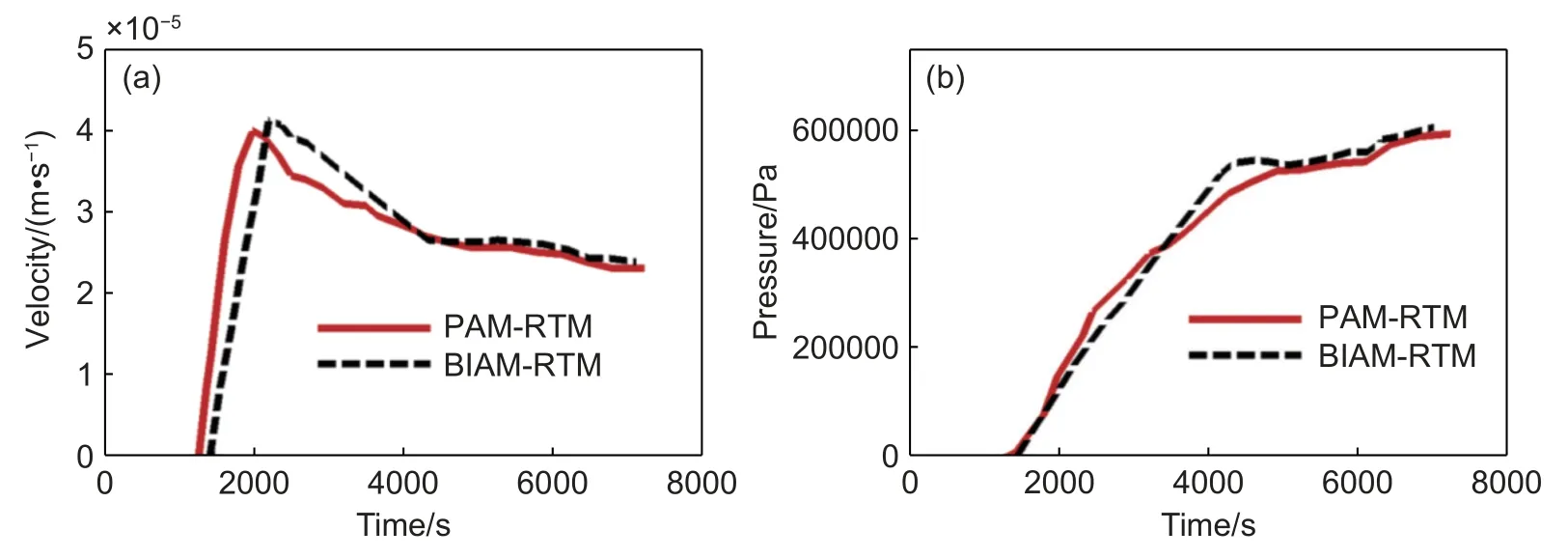
可采用控制体填充系数f来描述树脂流动的前锋。充填系数f代表了树脂填充控制体的情况，当f=1 时，树脂已完全充满控制体；当f<1 时，树脂未充满控制体；当f=0 时，树脂尚未流动到该控制体，属于未充填区域。在流动的前锋，充填系数f介于0 和1 之间，统计所有满足0

在算法设计中，为保证数值解在时间和空间方向互不影响，在能量方程求解中采用了半离散方法；为减小因分离式求解多个方程带来的数值误差，采用了一种三收敛标准[10]。下面对半离散方法和三收敛标准做简要概述。

（1）半离散方法

能量方程的求解采用了半离散的控制体/有限元方法，半离散方法将空间偏导数项的离散和时间方向的推进完全分开，可使空间的误差和精度等与时间推进的稳定性、收敛的加速性等无关。经过空间离散，能量方程就转化为了如下形式：

式中：P(T)为空间离散后关于不同控制体上温度T的线性组合，方程由原来的偏微分方程转化成了形式上的常微分方程，在时间方向推进即可求得方程的解。本工作在能量方程的时间方向采用了四阶Runge-Kutta（龙格-库塔）方法，该方法可以构造高精度来求解初值问题，至今仍为实际应用的重要方法。四阶 Runge-Kutta 方法的具体计算格式如下：

（2）三收敛标准

在与非等温相关的方程如能量方程、固化动力学方程的求解中，采用了分离式求解算法。虽然方程的求解得到了较大的简化，但也容易因为更新的滞后造成误差的累计从而引起数值解的不准确。基于以上考虑，本工作采用了一种三收敛的标准，在算法中设计了一个内循环，具体表述为：在一个时间步内，压力和速度计算完成后，就进入到非等温场的计算内循环中，只有当温度场、黏度场、固化度场均循环收敛时，才会跳出该循环进入下一个时间步。

1.3 验证模型

仿真模型采用C++语言进行了求解器的开发，基于QT 及python 语言进行了前后处理器的开发，仿真模型命名为BIAM Composites-RTM（简称BIAM-RTM）。仿真模型可模拟各种复杂的构件和多种工艺工况，最终得到压力场、速度场、温度场等仿真结果。验证模型选取了平板实验件和工程大型零部件机匣，现对两个验证模型如下说明。

北京航空航天大学段跃新团队对复合材料平板实验件进行了工艺实验。平板实验件几何模型如图2（a）所示，其尺寸为32 cm×32 cm，树脂黏度为0.062 Pa•s，玻璃布渗透率为9.7092×10−10m2，纤维含量为29%，模腔厚度5 mm，底边线恒压注射，注射压力为0.02 MPa，实验充填时间为114 s。

图2 验证模型的几何（a）平板实验件；（b）机匣件Fig. 2 Geometry of verification models （a）flat test piece；（b）receiver piece

随后，选取航空发动机零件中典型机匣件进行了应用验证。机匣复合材料实验件几何模型如下图2（b）所示，其半径尺寸为0.42 m，高0.25 m，树脂黏度为0.19 Pa•s，预制件渗透率为径向4.94×10−13m2，纤维体积含量为52%，底边线恒压注射，注射压力为1.2 MPa，实验充填时间为7200 s。

2 结果与讨论

2.1 平板实验件应用验证

应用BIAM-RTM 对平板件进行了数值模拟，工艺参数与实验条件保持一致。BIAM-RTM 仿真结果如图3 所示。图中分别给出了四个不同时刻（5.76、19.19、53.73、105.56 s）的填充度f和对应的压力分布情况。底边线同时进胶，前锋点位于同一高度上，随着不断注胶，前锋点向上平直推进，在同一高度上的压力值也基本平直。由于平板件实验中无法得到某点处的速度和压力值随时间变化曲线，为了验证仿真结果的可靠性，本工作采用PAMRTM 对平板件进行了相同工况的数值模拟。

图3 平板件填充度f 和压力P 随时间的变化（a），（e）t=5.76 s；（b），（f）t=19.19 s；（c），（g）t=53.73 s；（d），（h） t=105.56 sFig. 3 Variations in fraction and pressure of flat piece over time （a），（e）t=5.76 s；（b），（f）t=19.19 s；（c），（g）t=53.73 s；（d），（h） t=105.56 s

PAM-RTM 在RTM 工艺模拟方面非常强大，具有较高可靠性而受到业内的广泛认可和好评。PAMRTM 充填时间为115.586 s，与实验结果114 s 接近。表1 给出了两款软件与实验充填时间的对比误差。

表1 平板件BIAM-RTM 与PAM-RTM 充填时间与实验对比误差Table 1 Relative error of filling time compared to the experimental result of BIAM-RTM and PAM-RTM on flat piece

取平板件中心点的结果与PAM-RTM 仿真结果进行比对，速度及压力的对比曲线如图4 所示，两款软件仿真结果较为接近，趋势吻合较好。取峰值点进行定量比对，BIAM-RTM 的速度在峰值为0.00282 m/s，PAM-RTM 为0.00273 m/s，误差为（ 0.00282-0.00273） /0.00273=3.30%。 BIAM-RTM的压力在峰值为0.01090 MPa ，PAM-RTM 为0.01122 MPa，误差为（0.01122-0.0109）/0.01122=2.85%。

图4 平板实验件中心点处两款软件速度和压力随时间变化曲线（a）速度；（b）压力Fig. 4 Curves of velocity and pressure versus time between two softwares for the center point of flat test piece （a）velocity；（b）pressure

由以上分析可得出结论，BIAM-RTM 在平板件的模拟对比中，充填时间与实验结果和PAMRTM 仿真结果基本相当；中心点处的速度和压力与PAM-RTM 结果吻合较好，速度峰值点和压力峰值点与PAM-RTM 结果较为接近。

2.2 机匣件应用验证

采用BIAM-RTM 对机匣件进行了模拟，模拟结果如图5 所示，图中分别给出了四个不同时刻（58.64、1257.38、2255.89、5846.90 s）下填充系数f和压力的分布情况。底边线同时进胶，在相同高度下填充系数和压力值近乎相等。BIAM-RTM 模拟充填时间为7076 s，与实验结果7200 s 较为接近。同样采用PAM-RTM 在同样工艺条件下对机匣件进行了数值仿真，PAM-RTM 得到的充填时间为7206 s。表2 给出了两款软件模拟充填时间与实验值的对比误差，误差在2%范围内。

表2 机匣件BIAM-RTM 与PAM-RTM 充填时间与实验对比误差Table 2 Comparison error of filling time between BIAMRTM and PAM-RTM

图5 机匣件填充度f 和压力P 随时间的变化（a）填充度；（b）压力；（1）t=58.64 s；（2）t=1257.38 s；（3）t=2255.89 s；（4）t=5846.90 sFig. 5 Variations in fraction and pressure of receiver piece over time （a）f；（b）p；（1） t =58.64 s；（2） t =1257.38 s；（3） t =2255.89 s；（4）t =5846.90 s

在同一高度上的控制体具有相同的模拟结果，取机匣轴向中间位置任意点结果进行比对，速度及压力的对比曲线如图6 所示。观察图6，从整体来讲，BIAM-RTM 与PAM-RTM 模拟结果吻合较好，压力和速度在上升段的斜率不同，但在工艺末期，速度和压力值基本吻合。取峰值点进行比对，BIAM-RTM 的压力在峰值为533230 Pa ，PAMRTM 软件为503812 Pa，误差为（533230−503812）/503812=5.84%； BIAM-RTM 的速度在峰值为0.04094 mm/s，PAM-RTM 为0.0393 mm/s，误差为（0.04094-0.0393）/0.0393=4.17%。

图6 机匣件中间点两款软件速度和压力随时间变化曲线（a）速度；（b）压力Fig. 6 Curves of velocity and pressure versus time between two softwares for the midpoint of the receiver piece （a）velocity；（b）pressure

由以上分析可得出结论，针对机匣件的模拟结果，自研软件BIAM-RTM 与对标软件PAM-RTM在充填时间、速度及压力的仿真结果吻合较好，相对误差在6% 范围以内。