繁星树线图的完美匹配数
2023-06-13叶银珠陈海燕
叶银珠,陈海燕
(集美大学理学院,福建 厦门 361021)
图的完美匹配不仅在图论和计算科学中起着重要的作用,而且在统计物理和量子化学中占有重要的地位.在统计物理中,完美匹配被称为dimer构型[1],在量子化学中,完美匹配被称为Kekulé结构[2-4].众所周知,计算图的完美匹配数是一个NP-hard问题[5-7],受到学者高度的关注.
给定一个图G=(V,E),图G的线图用L(G)表示,是顶点集V(L(G))=E(G)的图,其中L(G)中的顶点e和f相邻当且仅当e和f是G中相邻的边.Sumner[8]和Vergnas[9]证明了每个具有偶数个顶点的连通无爪图至少有一个完美匹配.因为每个线图都是无爪的,所以具有偶数条边的连通图的线图一定有完美匹配.Dong等[10]给出了偶数条边树的线图完美匹配数表达式.本文主要利用此表达式来确定一类繁星树线图的完美匹配数的最大值和最小值.
令G=(V,E)是顶点数为n,边数为m的图,对于v∈V,v的度表示为dG(v)或d(v).若dG(v)=1,则顶点v称为G的悬挂点,其关联的边称为悬挂边.边子集M⊆E称为G的一个匹配,如果M中没有两条边关联同一个顶点.一个匹配M称为G的一个完美匹配,如果G的每个顶点都与M中的一条边相关联.G的完美匹配数用M(G)表示.对任意图G,令p(G)表示G的具有偶数条边的分支数.令S1,k表示k+1个顶点的星形树.一棵树T被称为繁星,如果它可以通过在一棵星形树的悬挂点添加悬挂边得到.
给定任何非负整数k,定义
(2k)!!=(2k-1)!!=(2k-1)(2k-3)…3·1,
其中0!!=(-1)!!=1.
引理1[10]设T是顶点集为{v1,v2,…,vn}的一棵树,其中n>1且为奇数,那么
1 繁星树线图的完美匹配数


图1 星和繁星Fig.1 Star and blossomed star
定理1设k和l是两个正整数,对任意T=T(t1,t2,…,tk)∈Tk,l有
其中r表示t1,t2,…,tk中偶数的个数.
证明∀v∈V(T),很显然若dT(v)≤2,则p(T-v)!!=1.因此只需要考虑p(T-u)和p(T-vi)(i=1,2,…,k).T-u有k个分支,每个分支的边数分别为t1,t2,…,tk,所以p(T-u)=r.T-vi有ti+1个分支,其中ti个为孤立点,剩下的一个分支有l+k-ti-1条边,所以
由引理1得
证毕.

2 繁星树线图完美匹配数的最小值

πi,j(T(t1,…,ti,…,tj,…,tk))=
T(t1,…,ti-2,…,tj+2,…,tk),ti≥2;
θi,j(T(t1,…,ti,…,tj,…,tk))=
T(t1,…,ti-1,…,tj+1,…,tk),ti≥1.

(i) 若ti与tj有同样的奇偶性,则
M(L(T))≥M(L(πi,j(T))).
(ii) 若ti与tj有不同的奇偶性,则
M(L(T))≥M(L(θi,j(T))).
证明对(i),由πi,j的定义和定理1易得
(1)
当ti和tj都是偶数时,式(1)等于
当ti和tj都是奇数时,式(1)等于
所以只要ti与tj同奇偶,都有
M(L(T))≥M(L(πi,j(T))),
(i)得证.
对(ii),由θi,j的定义和定理1可得
(2)
当ti为偶数,tj为奇数时,式(2)等于
当ti为奇数,tj为偶数时,式(2)等于
因此M(L(T))≥M(L(θi,j(T))).(ii)得证.
令

∀i,j,|ti-tj|≤2}.





0≤x≤k-b且与k-b同奇偶};




当b+x1-x3=k,即c=a+1,这时
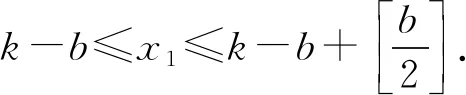


M(L(T*))=f(x)=

M(L(T*))=f(x)=
证明注意到k+l是偶数,由l=ka+b得,当a是偶数时,k-b一定是偶数,当a是奇数时,b一定为偶数.所以由引理3和定理1,结论马上得证.

(i) 若a是偶数,
M(L(T))≥
(ii) 若a是奇数,
M(L(T))≥

(i) 当a是偶数时,由引理4,当0≤x 所以当0≤a≤k-b时,x=a是f(x)在其定义域内的最小值点,即 (ii) 当a是奇数时,由引理4,当0≤x 所以当a≥k-1时,f(x)在整个定义域上是增函数. 当b-1≤a≤k-1, 当a≤b-1, 结论得证. φi,j(T(t1,…,ti,…,tj,…,tk))= T(t1,…,ti+tj,…,0,…,tk),ti,tj≥1. 证明令r,r′分别表示T-u,φi,j(T)-u中偶数条边的分支个数,则由φ-变换的定义得 所以由定理1可得, 因此M(L(T))≤M(L(φi(T))).结论得证. 定理4设k和l是两个正整数,对任意T=T(t1,t2,…,tk)∈Tk,i,有 M(L(T(t1,t2,…,tk)))≤ 注:定理3和定理4证明过程中借助了一系列变换,但这些变换不是严格单调的,除了证明中给出的繁星达到最值外,还可能存在其他繁星达到最值,因此存在下面的问题. 问题:分别确定出定理3和定理4中等号成立的所有极图.


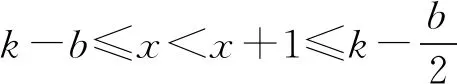

3 繁星树线图完美匹配数的最大值



