通道层流场中单颗粒惯性横向迁移的数值研究

魏良俊 ，王昊利

1.盐城工学院 机械工程学院，江苏 盐城 224051；2.金陵科技学院 机电工程学院，江苏 南京 211169

21世纪60年代，Segré等［1］首先发现了均匀散布细颗粒的流体以层流形式进入直管，经过长距离的流动后细颗粒会自发地进行径向迁移，最终受惯性力的影响聚集在管道内部的环形空间。这种现象称为“惯性聚集”，其主要特点是无需施加任何外力，就可以在微通道内对一定尺寸的颗粒进行聚集，从而实现对其分离与过滤。

为了解释颗粒在管内层流中迁移形成的惯性聚集现象，国内外学者对颗粒在宏观流场中运动所受作用力进行了大量的研究，提出颗粒在惯性层流场中受到Magnus 力［2］、Saffman 力［3］和剪切梯度力［4］等横向力的共同作用。早期有学者运用“摄动法”等理论方法研究了弹性颗粒在低雷诺数的简单剪切流场中的力学特性，发现弹性颗粒外形的变化也会导致颗粒产生横向迁移［5-6］；Carlo［7-8］等研究表明，在不考虑颗粒自转的情况下，“惯性聚集”现象依然存在，引发“惯性聚集”现象的横向迁移是流场惯性力作用的结果；Zhao等［9］利用计算流体动力学（computational fluid dynamics，CFD）方法模拟了具有弱弹性的颗粒在二维通道内的“惯性聚集”特点，表明颗粒的弹性变形会产生一个指向管道轴心的附加横向升力，且越靠近壁面，附加升力就越大；Nakayama 等［10］通过实验测量和数值模拟对圆管中悬浮颗粒的惯性聚集现象进行了研究，发现随着雷诺数的增加存在3 个区间对应着不同的惯性聚集分布；Miura等［11］研究了雷诺数为100～1 200 的方形流道中悬浮球形颗粒的惯性迁移，发现雷诺数大于250 时方管内部截面上存在8 个平衡位置，分别位于通道截面中心和角落，并且随着雷诺数的增加，颗粒愈发向通道中心和拐角处聚集；Raffiee 等［12］使用三维数值模拟研究了黏弹性流体中粒子的升力分布，预测了不同参数下的平衡位置，分析了不同平衡点的稳定性；Yu等［13］采用虚拟域方法对方形直流道内中性粒子的聚焦平衡位置进行了研究，发现随着流体弹性的增加，平衡位置连续出现在横截面的中线、对角线、拐角和流道的中心；全列［14］采用了格子玻尔兹曼方法，对中性悬浮球形颗粒在不同形状管道中的输运过程进行数值模拟，发现随着雷诺数的增加多颗粒成链现象更加明显，在轴对称的圆管和矩形管中颗粒惯性迁移轨迹在横截面上的投影分别是一条直线和一条曲线；高增锋［15］利用FLUENT 对二维平面通道中单颗粒的惯性迁移进行了模拟，指出了黏性流体中颗粒惯性迁移现象的根本原因和颗粒所受惯性升力沿颗粒的横向位置呈现规律性的空间分布。

为研究颗粒惯性聚集机制，本文采用计算流体动力学方法对圆管和方管内随流体运动的单个颗粒的横向迁移进行模拟研究。将颗粒放在进口截面的若干不同位置并释放，采用离散颗粒模型（discrete particle model，DPM）计算颗粒在流场中的迁移轨迹及横向迁移后所达到的平衡位置。

1 颗粒两相流基本方程

对于颗粒两相流，分别考虑连续相（流体）控制方程与离散相（颗粒）运动方程。

1.1 连续相控制方程

连续相控制方程考虑不可压缩的牛顿流体，满足连续性方程和动量方程，分别如下：

（1）连续性方程：

（2）动量方程：

式中：∇为Hamilton 算子；uf为流体流动速度，m/s；t为流体在管道中的流动时间，s；p为流体的压强，Pa；ρf为流体密度，kg/m3；v为流体运动黏度，m2/s。

1.2 离散相运动方程

对于离散相模型，基于拉格朗日坐标系，颗粒从进口点开始跟踪，直到离开流场或者满足某种积分极限准则为止。离散相方程包括：

（1）颗粒轨迹方程：

（2）颗粒动量方程：

式中：Xp为颗粒的质心位置，m；up为颗粒的速度，m/s；mp为颗粒的质量，kg；g为重力加速度，m/s2；Fd为颗粒受到的绕流阻力，N；FVM为颗粒受到的附加质量力，N；FB为Basset 力，N；FP为压力梯度力，N；FML为Magnus 力，N；FS为Saffman 力，N；FX为其余外力的综合，N。

2 颗粒横向受力分析

根据已有的研究，颗粒在层流场中的横向受力主要包括Magnus 力、Saffman 力以及剪切梯度力等，其力学特征和相关数学表达分别如下：

（1） Magnus力

当一个旋转物体的角速度矢量与位移速度矢量不重合时，在与角速度矢量和位移速度矢量组成的平面相垂直的方向上产生一个横向力，这个横向力就是Magnus 力。在Magnus 力的作用下，物体位移轨迹会发生偏转，这种现象称作马格努斯效应。

Magnus力表达式如下：

式中：d为颗粒直径，m；ω为流体旋转的角速度，rad/s。

（2） Saffman力

流过颗粒表面的流体具有不同的速度，在颗粒表面会产生一个由低速流体侧指向高速流体侧的横向作用力，这个横向作用力就是Saffman力，表达式如下：

式中：K为一常数，通常取6.46；μ为流体动力学黏度，Pa·s。

（3） 剪切梯度力

根据伯努利原理，当流体对颗粒具有相对运动速度时，在垂直于颗粒运动方向上会产生一个力，这个力就是剪切梯度力，表达式如下［16］：

式中：G为剪切梯度力，N；ΔP为颗粒上下表面的压力差，Pa；ΔH为颗粒上下表面的距离，m。

3 颗粒横向迁移数值模拟

为研究颗粒横向迁移情况，本文以中性悬浮单颗粒在液相层流通道内的稳定运动为研究对象，忽略质量力和颗粒对流场的影响，采用“颗粒点源”直接数值模拟方法进行通道层流场中颗粒的惯性迁移研究。该方法将颗粒当作一个质点，对液相采用欧拉法建立控制方程，用拉格朗日方法模拟颗粒在流场中的运动；在流场计算基础上，对颗粒引入Saffman力和剪切梯度力进行计算和轨迹追踪，暂未考虑颗粒旋转所产生的Magnus力的影响，主要原因是颗粒旋转作用效果有限。

3.1 通道模拟与边界设置

基于现有条件，采用计算流体动力学软件FLUENT（2021 R1）对圆管和方管在层流场中的颗粒惯性迁移开展数值模拟研究。边界条件为：进口速度条件设置为截面平均速度，具体数值根据设定的Re，按照式（8）反算计算求得；出口为压力出口；壁面为无滑移边界条件。在计算过程中，压力、速度的耦合采用SIMPLE算法计算。

式中：U为流经通道截面流体的平均速度，m/s；Re为雷诺数；l为管道特征长度，对于圆管为半径，方管取当量直径，m。

矩形管当量直径公式为：

式中：a、b分别为矩形管矩形截面中两条边的长度，m。

表1 给出了不同雷诺数下，流经圆管和方管截面流体的平均速度。

表1 不同雷诺数下通道截面流体的平均速度Table 1 Average velocity of channel section fluid at different Re m/s

3.2 网格划分与迁移计算

3.2.1 圆管

圆管通道模型中的圆管直径为9.6 mm，长度为1.0 m，管内流体为水。模型的坐标原点建在圆管进口截面中心处，如图1 所示，其中X轴为流体的流动方向，Y和Z为横向坐标轴。颗粒释放的初始位置位于进口截面的r0=0、0.7R、0.8R的点，如图2 所示。图2 中R为圆管截面的半径，r0为颗粒初始位置的半径。

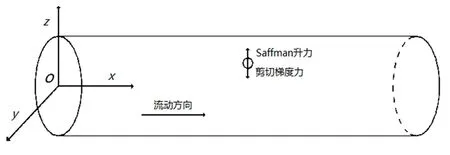
图1 部分圆管模型及颗粒横向受力示意图Fig. 1 Schematic diagram of partial circular tube model and lateral forces on particles

图2 颗粒在圆管进口处释放时的位置示意图Fig. 2 Schematic diagram of particle release position at the entrance of circular tube

模拟计算前首先用ICEM 软件对圆管进行网格划分，得到161 万六面体结构化网格，如图3 所示。为研究颗粒横向迁移情况，以圆管半径R为特征长度对颗粒的位置信息进行无量纲处理，假设颗粒在某时刻所处位置坐标为 （x1，y1，z1），则颗粒的无量纲流向与径向的位移x′、r′分别为：

图3 圆管局部网格图Fig. 3 Local grid diagram of circular tube

3.2.2 方管

方管通道模型中的方管边长为9.1 mm，长为1.0 m，管内流体及流向与圆管相同。模型的坐标原点建立在方管的进口截面中心处，坐标系同图1。颗粒释放的初始位置位于进口截面的z0=0、0.22L、0.33L处，如图4 所示。图4 中L为方管正方形截面边长，z0为颗粒初始位置的z轴坐标。

图4 颗粒在方管进口处释放时的位置示意图Fig. 4 Schematic diagram of particle release position at the entrance of square pipe

使用ICEM 软件对方管进行网格划分，得到156万个六面体结构化网格，如图5所示。为研究颗粒横向迁移情况，以正方形截面边长L为特征尺度对颗粒的位置信息进行无量纲处理。根据文献［13］报道的颗粒迁移数据以及本文大量仿真模拟结果，当颗粒释放位置在方管入口截面的中心对称线上时，其在管道内的迁移轨迹近似在同一平面内。假设颗粒释放位置为（0，0，z0），在某时刻颗粒所处的位置坐标为（x2，y2，z2），则颗粒的无量纲流向与径向位移x″、z″分别为：

图5 方管局部网格图Fig. 5 Local grid diagram of square tube

4 模拟与分析

4.1 圆管

4.1.1 圆管内速度场的模拟

为研究圆管内颗粒横向迁移规律，对直径为9.6 mm、长度为1.0 m、管内流体为水、具有161万个六面体结构化网格的圆管，在未加入颗粒、雷诺数Re=100 时，通过流体动力学软件FLUENT（2021 R1）对圆管中的流体速度场进行模拟，得到圆管内流体流向最大截面的局部速度，如图6 所示。从图6 可以看到，速度场经过了短暂的进口段之后，进入充分发展段。

图6 圆管内流向最大截面的局部速度云图Fig. 6 Local velocity nephogram of the maximum cross section of circular tube flow direction

4.1.2 圆管中颗粒的横向迁移

在图6 速度场基础上，采用离散颗粒相计算方法，对粒径d=0.8、1.0、1.2 mm 的中性球形颗粒，在雷诺数Re=100、125、150 条件下，在进口截面r0=0、0.7R、0.8R的3个初始位置释放的迁移过程分别进行计算，得到圆管内流场中的颗粒迁移轨迹及横向迁移后所达到的平衡位置，如图7～图10 所示。计算时仅考虑流体对颗粒的单向作用，不考虑颗粒对流场的反作用。

图7 颗粒在r0=0处释放的迁移轨迹Fig. 7 Migration trajectory of particles release when r0=0

图8 颗粒在r0=0.7R、0.8R处释放的迁移轨迹Fig. 8 Migration trajectory of particles release when r0=0.7R and 0.8R

图9 不同Re时颗粒在圆管内的迁移轨迹Fig. 9 Migration trajectory of particles with different Re in a circular tube

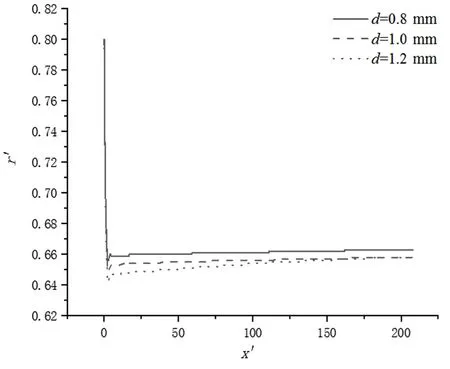
图10 不同粒径时颗粒在圆管内的迁移轨迹Fig. 10 Migration trajectory of particles with different sizes in a circular tube

图7 给出了Re=100、d=0.8 mm，Re=150、d=1.0 mm，Re=100、d=1.0 mm 时，颗粒在圆管进口截面中心即r0=0 处释放的迁移轨迹。从图7 可以看到，虽然存在横向迁移现象，但3种情况下颗粒最大横向迁移距离仅为0.008R，可以忽略不计。产生偏移的主要原因可能是由于数值波动，不具有明确的物理意义。

图8 给出了直径d=1.0 mm 的颗粒在圆管进口截面r0=0.7R、0.8R处释放时的迁移轨迹。从图8 可以看到，颗粒迁移过程经历了初始和平衡两个主要阶段，在初始阶段主要表现为颗粒跟随主流向下游运动的同时发生横向迁移；经过短暂的运动后，颗粒的横向迁移达到平衡阶段，其中，从r0=0.7R处释放的颗粒在r=0.57R的半径处达到平衡，从r0=0.8R处释放的颗粒在r=0.65R的半径处达到平衡。

图8 表明，颗粒在圆管内被层流向下游驱动时，会自发地进行径向迁移，最终会稳定地停留在离管道轴心约0.6倍半径的位置上并向下游继续运动。该模拟结果与Segre 等［1］的实验观测结果基本吻合。

图9 给出了粒径d=1.0 mm 的颗粒在r0=0.8R处释放时在不同雷诺数下的迁移轨迹。从图9可以看到，当Re=100、125、150 时，颗粒分别在r=0.658R、0.665R、0.672R处达到平衡。显然，随着Re的增加，圆管内颗粒惯性迁移的平衡位置向管壁方向偏移，而且从r0=0.7R处释放的颗粒也具有相似的规律。

图10 给出了Re=100、不同直径的颗粒在r0=0.8R处释放时的迁移轨迹。从图10 可以看到，当d=0.8、1.0、1.2 mm 时，颗粒分别在r=0.660R、0.658R、0.657R处达到平衡。显然，随着粒子尺寸的增加，圆管内颗粒惯性迁移的平衡位置将向管道轴心偏移，而且从r0=0.7R处释放的颗粒也具有相似规律。

4.2 方管

4.2.1 方管内速度场的模拟

为研究方管内颗粒横向迁移规律，对边长为9.1 mm、长度为1.0 m、管内流体为水、具有156万个六面体结构化网格的方管，在未加入颗粒、雷诺数Re=100 时，通过流体动力学软件FLUENT（2021 R1）对方管中的流体速度场进行模拟，得到方管内流体流向最大截面的局部速度，如图11所示。从图11可以看到，速度场经过了短暂的进口段之后，进入充分发展段。

图11 部分方管中心截面的局部速度云图FIg. 11 Local velocity nephogram of central section of partial square tube

4.2.2 方管中颗粒的横向迁移

在图11 速度场基础上，采用离散颗粒相计算方法，对粒径d=0.8、1.0、1.2 mm 的中性球形颗粒，在雷诺数Re=100、125、150 条件下，在进口截面z0=0、0.22L、0.33L的3 个初始位置释放的迁移过程分别进行计算，得到方管内流场中的颗粒迁移轨迹及横向迁移后所达到的平衡位置，如图12～图15所示。计算时仅考虑流体对颗粒的单向作用，不考虑颗粒对流场的反作用。

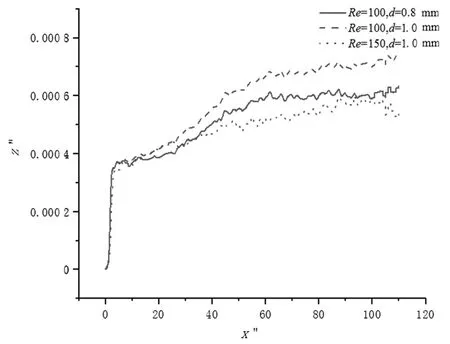
图12 颗粒在z0=0处释放的迁移轨迹Fig. 12 Migration trajectory of particles released at z0=0

图13 颗粒在z0=0.22L、0.33L处释放的迁移轨迹Fig. 13 Migration trajectory of particles released at z0=0.22L、0.33L

图14 不同Re时颗粒在方管内的迁移轨迹Fig. 14 Migration trajectory of particles with different Re in a square tube

图15 不同粒径时颗粒在方管内的迁移轨迹Fig. 15 Migration trajectory of particles with different sizes in a square tube

图12 给出了Re=100、d=1.0 mm，Re=150、d=1.0 mm，Re=100、d=0.8 mm 时，颗粒在方管进口截面中心即z0=0 处释放的迁移轨迹。从图12 可以看到，方管与圆管规律相似，均存在横向位移现象，但数值可以忽略不计，即不具有明确的物理意义。

图13 给出了颗粒在方管进口截面z0=0.22L、0.33L处释放时的迁移轨迹。从图13 可以看到，当释放位置为z0=0.22L时，颗粒迁移的平衡位置约在z=0.17L处；当释放位置为z0=0.33L时，颗粒迁移的平衡位置约在z=0.26L处。显然，释放位置越靠近管道轴心时，颗粒的横向迁移距离越短，也越容易达到平衡位置。

图14 给出了不同雷诺数条件下粒径d=1.0 mm 的颗粒在方管进口截面z0=0.33L处释放时的迁移轨迹。从图14可以看到，Re=100、125、150时颗粒迁移平衡位置分别位于z=0.256L、0.255L、0.254L处。显然，对于方管而言，在释放位置等其他条件相同的情况下，Re不同，颗粒最终的平衡位置亦有所不同；随着Re的增加，颗粒的平衡位置会更加偏向通道中心。颗粒从z0=0.22L处释放时也具有相似的规律。

图15给出了不同粒径条件下，Re=100、颗粒在z0=0.33L处释放时的迁移轨迹。从图15 可以看到，当d=0.8、1.0、1.2 mm 时，颗粒迁移的平衡位置分别位于z=0.260L、0.256L、0.248L处。显然，对于方管而言，在释放位置等其他条件相同时，粒径大小不同，颗粒迁移的平衡位置也不同，表现为小颗粒的平衡位置更加靠近壁面。颗粒从z0=0.22L处释放时也具有相似的规律。

5 网格数量对计算结果的影响

图16 给出了网络数量分别为141 万、161 万、211 万时，颗粒在圆管进口截面r0=0.8R处释放的迁移轨迹。从图16 可以看到，初始阶段3 个网格的迁移轨迹完全吻合；经过短暂迁移后，颗粒由初始r0=0.8R分别迁移至r=0.65R、0.64R、0.63R处达到平衡，相邻两种网格的计算偏差约为0.01R。显然，计算结果未随着网格数量增加产生明显变化，即计算结果与网格数量无明显关联，计算所得的颗粒横向迁移规律具有可信度。

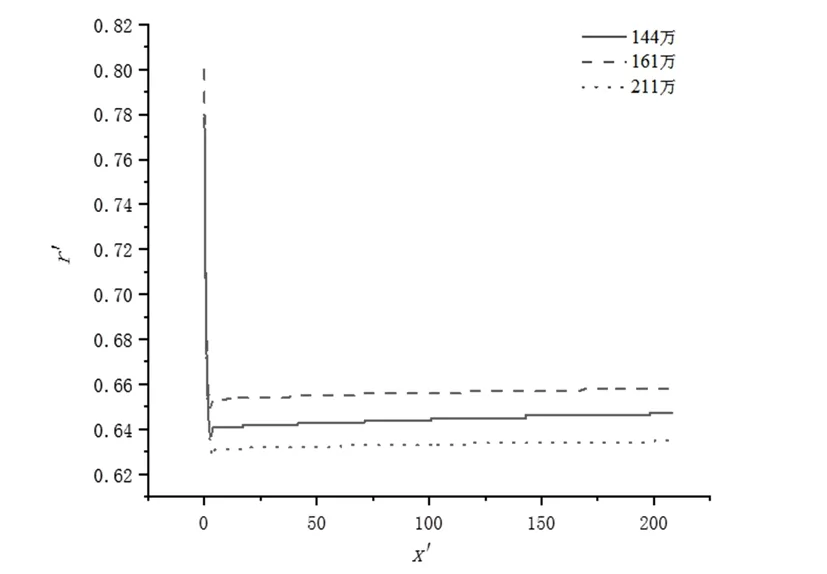
图16 不同网格数的圆管对颗粒迁移结果的影响Fig. 16 Influence on particles release in different grid numbers of circular tube

图17给出了网络数量分别为125 万、156 万、187 万时，颗粒在方管进口截面z0=0.33L处释放的迁移轨迹。从图17 可以看到，3 种网格下颗粒迁移最终在z=0.253L～0.257L处达到平衡。显然，不同网格方管计算结果偏差在合理范围内，说明方管计算结果与网格数量无显著相关性。

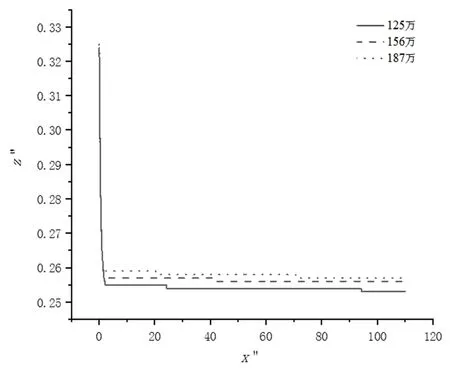
图17 不同网格数的方管对颗粒迁移结果的影响Fig. 17 Influence on particles release in different grid numbers of square tube

6 结论

通过对通道层流场中单颗粒横向惯性迁移的数值研究，得出如下结论：

（1）对于圆管，当雷诺数Re取100、125、150，颗粒直径d采用0.8、1.0、1.2 mm，释放位置r0=0.7R、0.8R时，颗粒惯性横向迁移的平衡位置约在r=0.6R附近，且随着粒子尺寸的增加，颗粒平衡位置将向管道轴心偏移；随着Re的增加，颗粒平衡位置向管壁方向偏移。

（2）对于方管，当雷诺数Re取100、125、150，颗粒直径d采用0.8、1.0、1.2 mm，释放位置z0=0.22L时，颗粒横向迁移的平衡位置约在z=0.170L附近；当释放位置z0=0.33L时，颗粒横向迁移的平衡位置约在0.255L附近。显然，释放位置越靠近通道轴心，颗粒的横向迁移距离越短；随着Re的增加，颗粒的平衡位置会更加偏向管道中心。此外，小颗粒的平衡位置更靠近壁面。

（3）网格数量对计算结果偏差的影响均在合理范围内，计算结果具有可信度。