海上风电直流汇集变换器改进型控制策略研究

潘 健 ，阚加荣 ，成 乾 ，夏晓燕 ，王 淼 ，刘 俊

1.盐城工学院 电气工程学院，江苏 盐城 224051；2.国网东台市供电公司，江苏 东台 224200

在海上风电传输过程中，直流汇集方式相较于交流汇集方式具有更经济、更可靠的优势，更加适用于远距离大规模的海上风力发电传输系统［1］。其中双有源桥变换器（dual active bridge，DAB）因具有效率高、能量双向流动的优点，且能够在海上风电场启动时为其提供能量，因此非常适用于海上风电的直流汇集。同时，在将多个DAB 变换器串并联后又可以满足海上风电高压大容量的传输需求。

在常用的DAB 变换器串并联拓扑结构中，输入并联输出串联结构（input-parallel and outputseries，IPOS）因输入侧并联可增大系统的电流水平、输出侧串联可提高系统的输出电压等级，在海上风电直流汇集中得到了广泛的应用。

在输入并联输出串联型的变换器电路中，输出侧均压是变换器正常运行的关键［2］。杨晓光等［3］针对LCC 谐振变换器，采用主从控制策略，但在海上风电直流汇集系统运行过程中，当主控制器发生故障时，从控制器也会受到影响，可靠性不高；Giri 等［4］采用了三环控制策略，控制相对复杂且成本较高；Giri 等［5］采用共用占空比控制，但因为器件导通时间及变压器漏感等存在差别，均压效果会受到影响。以上文献所提及的控制策略均是集中式控制策略，其系统的可靠性、冗余性都受到一定的影响。

针对集中式控制存在的问题，考虑采用分散式控制，其中的下垂控制策略因结构简单、冗余性好等优点得到广泛应用［6］。本文针对传统输入均流下垂控制策略下的IPOS-DAB 变换器存在静态偏差的问题，提出一种改进的输入均流下垂控制策略，即通过引入输入电流的平均值来减少输出电压的跌落，从而在实现各模块输入均流/输出均压的同时减小了系统的静态偏差；最后又通过仿真，验证其正确性。

1 IPOS-DAB拓扑系统结构

图1 为IPOS 变换器拓扑结构，图2 为两个DAB模块组成的IPOS-DAB 变换器拓扑结构。图1 中，Uin为总的输入电压，Uo为总的输出电压，Uoi为各模块的输出电压，Iin为总的输入电流，Io为总的输出电流，Iini为各模块输入电流。图2 中，Si1～Si8为IGBT 功率开关管，Li为各模块的储能电感，Cdi和Cfi分别为各模块输入侧电容和输出侧电容，R为负载电阻，n为变压器变比，其中i=1，2。

图1 IPOS变换器拓扑结构Fig. 1 IPOS converter topology

图2 两个模块的IPOS-DAB变换器拓扑结构Fig. 2 IPOS-DAB converter topology with two modules

文献［7-8］指出，对于IPOS结构而言，系统稳定运行须保证输入并联侧均流、输出串联侧均压。因此只要保证各DC/DC 变换器模块输入电流相等，就能保证其输出电压相等。同理只要保证各DC/DC 变换器模块输出均压，也就能保证其输入均流。

2 传统的输入均流下垂控制策略

为了使IPOS-DAB 变换器实现输入均流/输出均压，以图2 中的模块1 为例对传统的输入均流下垂控制策略进行分析。传统输入均流下垂控制策略框图如图3所示。

图3 传统的输入均流下垂控制策略Fig. 3 Traditional input current sharing droop control strategy

图3中，Uo1_f为模块1 的输出电压采样值，V；D1为模块1的移相占空比。

对于模块1 而言，输出电压参考值可以表示为：

式中：U*o1为模块1的输出电压参考值，V；Uref1为模块1 的输出电压基准值，V；k1为模块1 的下垂系数；Iin1为模块1的输入电流，A。

由式（1）可知，当变换器空载时，输入电流为零，输出电压无下降，输出电压参考值U*o1等于输出电压基准值Uref1；当输入电流不为零时，输出电压参考值U*o1随着输入电流Iin1的增加而降低，从而导致输出电压Uo1降低而产生静态偏差。

对于两个DAB 变换器模块而言，当系统稳定运行时各模块的输出电压满足：

式中：Uo1、Uo2分别为模块1、模块2的输出电压，V；Uref2为模块2 的输出电压基准值，V；k2为模块2 的下垂系数；Iin2为模块2的输入电流，A。

IPOS-DAB 变换器的输入电流、输出电压满足：

式中：Iin为总的输入电流，A；Uo为总的输出电压，V。

将式（3）代入式（2），可以推出各模块的输入电流：

将式（3）、式（4）代入式（2），得到两个模块的输出电压：

由于两个模块输出端串联，两个模块的输出电压基准值相等，即Uref1=Uref2=Uref。因此两个模块的输出电压表达式可简化为：

由式（6）不难看出，各模块的输出电压不仅与各模块的下垂系数ki（i=1，2）有关，还与总的输入电流有关。由于系统运行时输入电流不为零，各模块的输出电压总会存在静态偏差，从而达不到设定的预期值。

3 改进的输入均流下垂控制策略

针对传统输入均流下垂控制策略存在的上述问题，本文提出一种改进的输入均流下垂控制策略，如图4 所示。改进的输入均流下垂制策略由于两个模块的控制完全一致，因此模块2 的控制部分不再显示。

图4 改进的输入均流下垂控制策略Fig. 4 Improved input current sharing droop control strategy

图4中，将模块1 的输入电流与各模块输入电流均值之差以一定的比例反馈至系统的输出电压上。改进后模块1 的输出电压参考值表达式为：

式中：Iin_avg为各个模块输入电流的均值，A。

对比式（1）、式（7），可以看出在稳态情况下，如果各模块可以实现输入均流/输出均压，那么各模块输入电流与均值电流之差几乎为零，其反馈值对于输出电压参考值几乎没有影响。如果各模块无法实现输入均流/输出均压，那么由于Iin1-Iin_avg＜Iin1，各模块输入电流与均值电流之差将产生一个较小值，进一步反馈至输出电压参考值上，会控制直流变换器系统实现均流/均压，从而有效减小了系统的静态偏差。

同理，系统稳态时，图4中各模块的输出电压可以表示为：

将式（3）代入式（8），得到各模块的输入电流，分别为：

将式（3）、式（9）代入式（8），得到各模块的输出电压表达式：

由于两个模块输出端串联，两个模块的输出电压基准值相等，即Uref1=Uref2=Uref，因此两个模块的输出电压表达式可简化为：

对比式（6）、式（11），可以看出改进后的输出电压计算时引入输入电流平均值，并用输入电流平均值与各模块输入电流的差值代替各模块输入电流，来减小输出电压扰动。当系统处于稳态时，总的输入电流Iin与2Iin_avg的差值为零，输出电压等于输出电压的基准值，输出电压不再受输入电流的影响，因此输出电压没有跌落，从而减小了输出电压的静态偏差。

4 仿真验证

为了比较传统的输入均流下垂控制策略和改进的输入均流下垂控制策略的有效性，利用MATLAB/Simulink 仿真软件进行仿真验证。在Simulink 中搭建由2 台DAB 变换器构成的输入并联输出串联系统仿真模型，仿真参数如表1所示，总的输出电压Uo为5 000 V，两个模块输出电压Uoi（i=1，2）的预期值为2 500 V，仿真结果如图5～图7所示。

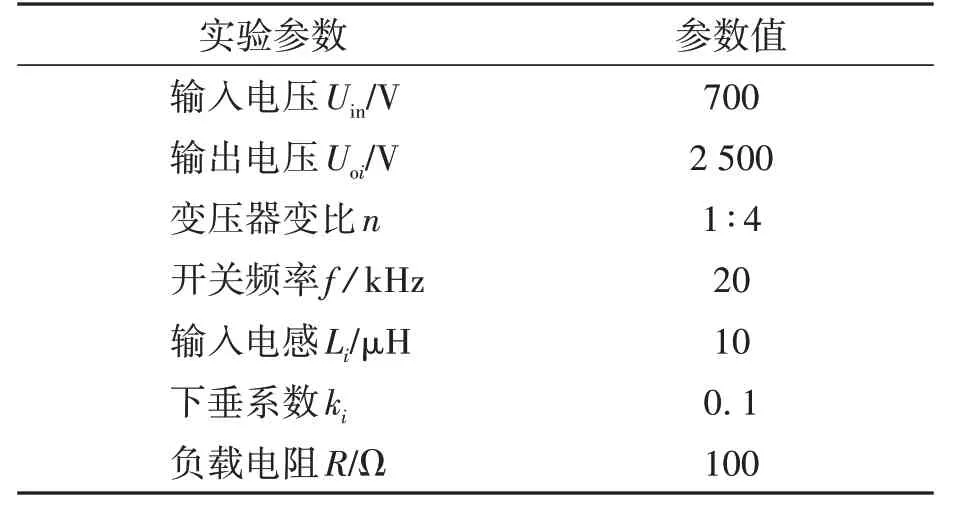
表1 仿真实验主要参数Table 1 Main parameters of simulation experiment

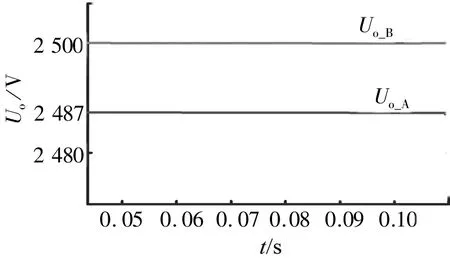
图5 IPOS-DAB变换器在传统和改进的控制策略下两模块的输出电压波形Fig. 5 The output voltage waveforms of the two modules of the IPOS-DAB converter under the traditional and improved control strategies

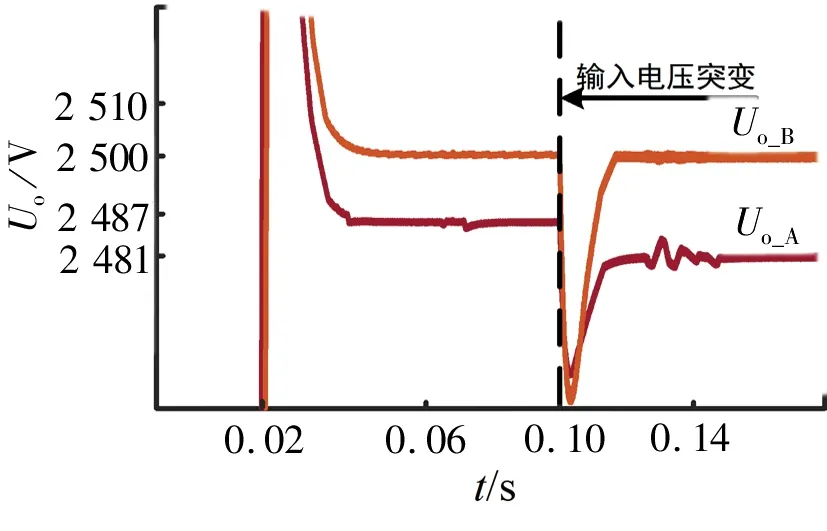
图6 输入电压突变时输出电压波形Fig. 6 Output voltage waveform when input voltage suddenly changes

图7 输出负载突变时的输出电压波形Fig. 7 Output voltage waveform when the output load suddenly changes

图5 给出了IPOS-DAB 变换器分别在传统和改进的输入均流下垂控制策略下两个模块的输出电压波形。图5中，Uo_A、Uo_B分别为传统与改进的下垂控制下两个模块的输出电压。由图5 可知，在下垂系数为0.1时，传统的输入均流下垂控制策略下，两模块输出电压Uo_A能够实现均压，但只能达到2 487 V 左右，未能达到预期设定的2 500 V；改进后的输入均流下垂控制策略下，两模块的输出电压Uo_B在实现均压的同时稳定在2 500 V，达到了预期的设定值。

图6 为传统和改进的输入均流下垂控制策略下，输入电压发生突变时两个模块的输出电压波形。由图6可知，在0.10 s时输入电压Uin由700 V突变为500 V，改进的输入均流下垂控制下的输出电压Uo_B在经过一个暂降后稳定在2 500 V；而传统的输入均流下垂控制策略下的输出电压Uo_A只能达到2 481 V 左右，未能达到预期要求，从而证明了改进的输入均流下垂控制策略在输入电压发生突变时的较高稳定性。

图7 为传统和改进的输入均流下垂控制策略下，负载发生突变时两个模块的输出电压波形。由图7可知，当系统在0.20 s时负载由100 Ω突变为90 Ω，输出电流增大，改进的输入均流下垂控制下的输出电压Uo_B经过暂降后稳定在2 500 V；而传统的输入均流下垂控制策略下的输出电压Uo_A只能达到2 443 V，未能达到预期的2 500 V，证明了改进的输入均流下垂控制策略在输出负载发生突变时的较高稳定性。

图8 为改进的输入均流下垂控制策略下，两个模块的电感L1、L2分别为10 μH、8 μH，而其他参数保持一致时输出侧子模块的电压波形。从图8 可以看出，改进的输入均流下垂控制策略下输入侧电感参数不一致时，两个模块在0.03 s 左右实现了均压，证明了改进的输入均流下垂控制策略取得了优良的均压效果。

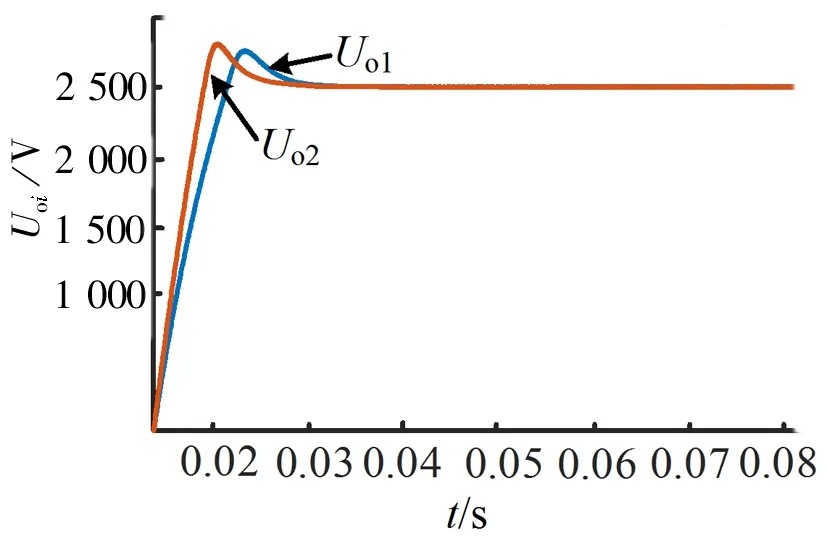
图8 输入侧电感参数不等时输出电压波形Fig. 8 Output voltage waveform when the input side inductance parameters are not equal

通过以上仿真结果可以看出，当IPOS-DAB变换器采用改进的输入均流下垂控制策略后，在系统输入电压发生突变、输出负载突变，以及电感参数不同的情况下均能实现均压，保证整个系统的稳定运行，并有效地减小了系统的静态偏差。

5 结论

针对IPOS-DAB 变换器在传统的输入均流下垂控制策略中存在的静态偏差问题，提出了一种改进的输入均流下垂控制策略。通过分析传统的输入均流下垂控制的运行特性，得出传统的输入均流下垂控制策略存在静态偏差的原因；在传统的输入均流下垂环节，引入模块输入电流均值来减小输出电压跌落，从而在实现各模块均压/均流的同时，减小了系统的静态偏差，提高了系统性能。仿真结果表明，改进后的输入均流下垂控制策略相较于传统的输入均流下垂控制策略，在输入电压发生突变、输出负载突变，以及电感参数不同的情况下，圴能使系统正常稳定地运行，并具有优良的均压效果。