无边界分布时滞惯性忆阻神经网络的反同步控制研究
2023-06-12何佳昊李小凡姚金泽
何佳昊,李小凡,姚金泽,黄 鑫
(盐城工学院 电气工程学院,江苏 盐城 224051)
自1971 年蔡少棠教授根据电路理论预测一种表示磁通与电荷关系的电路元件,并命名为忆阻器以来[1],惠普实验室于2008 年首次生产出纳米级的忆阻元件[2]。由于忆阻器的阻值是由流经它的电荷决定的,因此测量忆阻器的阻值,就能知道流经它的电荷量,这就是忆阻器的记忆特性。基于忆阻器的记忆特性,用忆阻器将传统神经网络硬件电路中的电阻替换掉,就可构建出适合模拟人脑的记忆神经网络,即忆阻神经网络[3-4]。
1986年,Babcock等[5]提出一种新的神经网络模型——惯性神经网络,并用二阶微分方程进行描述。目前,研究惯性忆阻神经网络动力学的主要方法是降阶代换法和非降阶法[6-7]。降阶代换法是通过合适的变量代换,将二阶微分系统转换成与之等价的两个一阶微分系统,再利用Lyapunov 稳定性理论来分析一阶微分系统的稳定性、反同步等动力学行为,进而得到原微分系统的相关结论。这种方法的缺点是降阶处理之后,原微分系统转换成两个一阶微分方程,其理论推导过程较为复杂,得到的结论也更加复杂。非降阶法是根据二阶微分系统构造Lyapunov 泛函,直接分析二阶微分系统的动力学行为,从而有效降低推导过程及结果的复杂度,并保留惯性特性。与降阶代换法相比,非降阶法更加简洁。
由于目前尚未见到用非降阶法来处理具有无边界分布时滞的惯性忆阻神经网络反同步问题的相关研究成果,基于上述分析,本文讨论了具有无边界分布时滞的惯性忆阻神经网络的反同步问题。主要方法是首先建立忆阻神经网络模型,然后引入惯性项和无边界分布时滞,最后通过非降阶法直接对无边界分布时滞的惯性忆阻神经网络模型进行动力学行为分析。
1 系统模型
假设具有无边界分布时滞的惯性忆阻神经网络模型如下:
式中:xi(t)为模型第i个神经元在t时刻状态变量,且其中s∈(-∞,0],表示由映射到n的所有连续函数构成的Banach空间,n表示n维欧氏空间);τj(t)为第j个神经元的传输时滞;fj(xj(t))为第j个神经元在t时刻不含时滞的激活函数;fj(xj(t-τj(t)))为第j个神经元在t时刻含有时滞的激活函数;Kij(t)为+→+上关于无边界分布时滞的非负延迟核心实值函数(+表示所有正实数的集合);θ表示积分变量;αi>0,βi>0;aij(xi(t))、bij(xi(t))、cij(xi(t))分别表示忆阻器权值,且
其中a′ij、a`ij、b′ij、b`ij、c′ij、c`ij均是常数,Υi为切换界值,且Υi>0。
假设1:激活函数fj(·)是利普希茨连续函数,存在常数Fj>0,使得|fj(yj(s)) -fj(xj(s))|≤Fj|yj(s) -xj(s)|,其中yj(s)、xj(s) ∈R,j= 1,2,…,n。
假设2:时滞τj(t)满足0 ≤τj(t) ≤τ1、τ̇j(t) ≤τ2<1,其中j= 1,2,…,n,τ1、τ2是正常数。
假 设 3:存 在 正 常 数κij,使 得其中i、j= 1,2,…,n。
针对式(1)的驱动系统,构造相应的响应系统,如式(2)所示。
式中:yi(t)为响应系统第i个神经元在t时刻的状态变量,且其中ui(t) 是自适应切换控制器。
根据反同步误差ei(t) =yi(t) +xi(t)及式(1)、式(2),可以将反同步误差系统描述为:
根据式(3)的反同步误差系统,可将自适应切换控制器ui(t)设计如下:
式中:γi(t)和ξi(t)是控制增益;ςi>0,ρi>0;mi(t)满足
式(3)是一个不连续的切换系统,具有Filippov 意义下的解,在式(4)自适应切换控制器控制下,基于集值映射和微分包含理论,式(3)的反同步误差系统可改写为:
式中:fj(ej(t)) =fj(xj(t)) +fj(yj(t)),fj(ej(t-τj(t))) =fj(xj(t-τj(t))) +fj(yj(t-τj(t)))。
根据式(1)的驱动系统和式(2)的响应系统,式(3)的反同步误差系统分2种情况讨论:
(1)当|xi(t)|≤Υi、|yi(t)|≤Υi或|xi(t)|>Υi、|yi(t)|≤Υi时,式(3)的反同步误差系统为:
(2)当|xi(t)|>Υi、|yi(t)|>Υi或|xi(t)|≤Υi、|yi(t)|>Υi时,式(3)的反同步误差系统为:
根据上述2 种情况,可得到反同步误差系统为:
式中:aij∈co[a′ij,a`ij],bij∈co[b′ij,b`ij]。
2 主要结论
定理1:在假设1~3 成立的条件下,存在常数αi>0、βi>0、ξˉi>0、γˉi>0,式(1)的驱动系统和式(2)的响应系统在式(4)自适应切换控制器的控制下可以实现反同步。
证明:构造Lyapunov泛函数
对式(9)求导,并将式(8)的误差系统代入Lyapunov泛函数的导数,得:
根据假设2,可知:
将不等式(11)~(16)带入式(10)的Lyapunov导数方程中,得
假设式(17)中ηi>0、ξˉi>0、γˉi>0,且满足如下条件
则有
从而式(1)的驱动系统和式(2)的响应系统在式(4)自适应切换控制器的控制下可以到达反同步。
3 系统仿真
在式(1)的无边界分布时滞惯性忆阻神经网络模型驱动系统中,n取2,构建新的神经网络模型驱动系统如下:
根据式(19),构造相应的响应系统如下:

图1 有、无自适应切换控制器的反同步误差曲线Fig. 1 Anti-synchronization error curve with and without adaptive switching controller
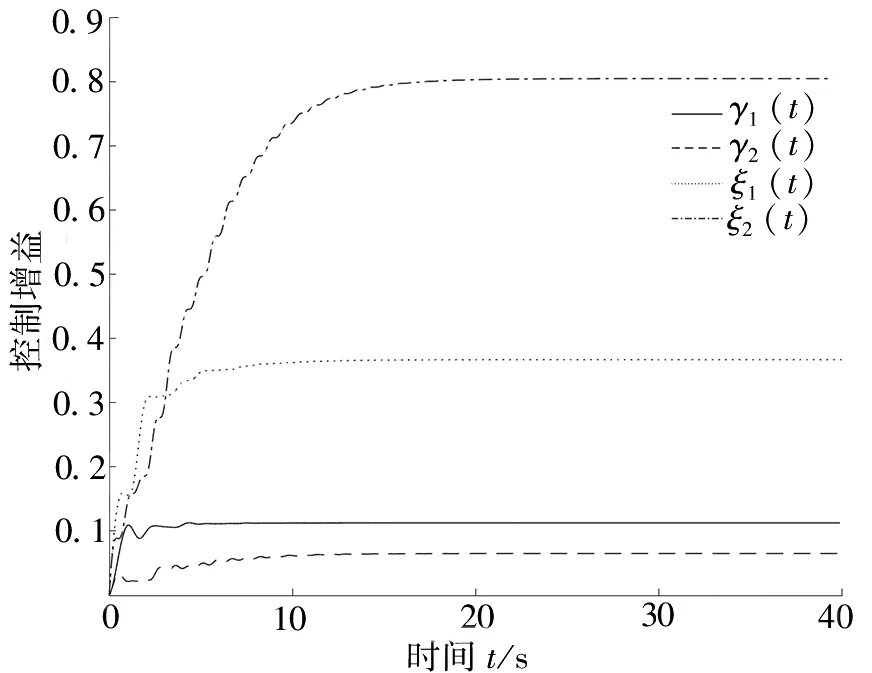
图2 自适应切换控制器的控制增益Fig. 2 Control gain of adaptive switching controller

图3 自适应切换控制器下的反同步曲线Fig. 3 Anti-synchronization curve under adaptive switching controller
由图1a 可知,无自适应切换控制器控制时,误差系统e1(t)和e2(t)的曲线呈现震荡的趋势,无法实现反同步;由图1b 可知,在自适应切换控制器的控制下,误差系统e1(t)和e2(t)的曲线均趋于零,实现了反同步。由图2可知,自适应切换控制器的控制增益γ1(t)、γ2(t)、ξ1(t)、ξ2(t)达到反同步后趋于稳定值。由图3a 可知,在自适应切换控制器控制下,驱动系统x1(t)和响应系统y1(t)的绝对值相同但符号相反,达到反同步;由图3b可知,在自适应切换控制器控制下,驱动系统x2(t)和响应系统y2(t)的绝对值相同但符号相反,达到反同步。
4 结论
本文在参考大量文献的基础上,采用非降阶法研究具有无边界分布时滞惯性忆阻神经网络的反同步问题,具体方法是设计一个合适的自适应切换控制器,再通过构造合适的Lyapunov 函数,利用不等式技术等得到惯性忆阻神经网络反同步的充分条件,最后通过数值仿真验证了设计的自适应切换控制器的有效性。以后在未来的研究中,将继续研究惯性忆阻神经网络的其他问题。
