加强小学数学开放题教学指导，培养创新思维

李林娟

摘  要：思维培养的根本目标是锻炼学生的思维能力，使学生在面对数学问题时可以灵活调用自身的抽象思维、逻辑思维等各种类型的思维来完成问题分析任务，快速找到解题突破口并完成问题求解任务。文章立足小学数学教学现状，重点对数学开放题教学中思维培养的意义与指导策略进行了探讨。

关键词：小学数学；思维能力；开放题；指导策略

一、思维培养的目标

思维培养的根本目标是有效锻炼及发展学生的思维能力，具体就是指导学生在参与学习活动过程中勤用脑、善思考，有效锻炼及发展其快速思维能力和反应能力，尤其是要注意指导学生在举一反三或者其他变式训练下，结合相关的差异化解题情况，对自己的学习思维进行有效反思，更好地完成相关学习活动中的分析以及其他综合性学习任务。期间还可以指导学生灵活地应用概括、推理、质疑、反思等一系列思维训练方式开展思维培训及训练。在各项活动开展过程中，要重点锻炼其思维的新颖性、发散性。在对思维进行培养期间，常用的方法包括设问法、变式训练、概括推理、创新思维训练以及一题多解和多变等。在数学学科知识学习或数学问题剖析过程中，随着学习难度的增加以及抽象概括需求的增加，学生的数学思维从直观思维向形象思维和逻辑思维发展，是符合学生思维发展逻辑、助力学生解题能力发展的必然选择。

二、小学数学开放题教学中思维培养的意义

所谓开放题，主要是指那些不具有完备条件和唯一答案的问题，相应地，问题本身呈现多样化特征，并且解题思路呈现发散性特征，开放题可以在有效促进学生学习数学知识的同时，促进其思维在严谨、创新、灵变、发散等方面得到发展，还可以展示其创造性和创新性才华，促进其推理分析能力、阅读理解能力以及问题求解能力等数学关键能力全面发展。开放题本身的题型形式复杂多变，其既可以条件开放，又可以结论开放等，但是无论开放题的“开放”特征处于何地，都要注意满足学生自思、自探或合作学习等多方面学习需求，力求借助开放题的设计及实施，让学生在调用自己思维能力求解问题的同时，进一步锻炼和发展自身思维能力，最终实现思维能力和开放题求解能力的全面发展，避免因为其中某个环节中的解题训练不到位或者指导不合理而直接影响学生思维能力的最终培养效果，可以抓住开放题设计及实施环节，促进小学生数学核心素养发展。

三、小学数学开放题教学中思维培养的指导策略

（一）巧设条件开放题，开展思维培养

条件是问题求解中需要重点关注的一个核心要素。通过科学设计条件开放题，可以对学生思维的严谨与深刻等特性进行有效锻炼，同时也可以培养学生的观察能力、问题发现能力和求解能力等综合能力。因此，在实际的开放题教学中，可以结合现阶段小学生的实际经验等，对问题的条件进行合理增删，或者借助改变条件的方式来使问题的求解答案不再具有唯一性，还可以在指导学生对相关开放题进行求解的过程中，有效锻炼其思维能力。但是为了保证条件开放题设计的效果，要注意指导学生重点对其中的有效条件进行挖掘，排除其中不必要的干扰因素，保证基于条件开放题的科学设计，促使学生可以在分析问题的过程中对问题本质进行准确把握，提高其求解数学条件开放题的效率与准确度。

例１：小明家和体育馆之间的距离是小冬家和体育馆之间距离的４倍，小冬家与体育馆之间的距离是６００米，他们两家之间距离是１５００米，某一天学校放假后小明从体育馆回到家里总计耗时３０分钟，试求小冬家和体育馆之间的距离是小明家和体育馆之间距离的百分之几？

解析：本道开放题是一道条件“多余”的问题，是一种比较多见的数学开放题，主要考查的是学生能否对问题求解中的多余干扰因素进行有效排除。在对这类开放题进行求解过程中，教师要注意指导小学生对题干信息认真审查，搞清相关问题的题目求解含义及目标，并要懂得在读题和审题的过程中，明确其中的关键题意，深入挖掘一切可以利用的有价值信息，保证在对多余干扰因素进行有效排除的基础上，快速确定解题的突破口及思路，最终助力学生快速求解问题。在本道开放题求解过程中，要想求解“小冬家和体育馆之间的距离是小明家和体育馆之间距离的百分之几”，首先必须要根据“小明家和体育馆之间的距离是小冬家和体育馆之间距离的４倍”与“小冬家距离体育馆的距离是６００米”来相应地推导出小明家和体育馆之间的距离，即４×６００＝２４００（米），这时候可得“小冬家和体育馆之间的距离是小明家和体育馆之间距离的百分之几”的计算公式为：６００÷２４００＝２５％。

通过指导学生认真剖析本道条件开放题，使他们通过认真审题来排除其中影响解题的多余干扰因素和条件，即“他们两家之间距离是１５００米”和“某一天学校放假后小明从体育馆回到家里总计耗时３０分钟”。一旦学生在求解本道开放题的过程中准确排除掉这两个干扰因素，那么最终就可以快速解决问题。由此可见，针对条件开放题的求解，在指导学生求解中要使他们懂得“排干扰”。

（二）巧设问题开放题，开展思维培养

问题开放题主要是开放题目中给出的问题不明确，需要学生在求解问题的过程中，通过自主思考和分析，补充问题求解的相关条件之后再进行求解。在这个过程中，小学生是独立开展学习活动的个体，他们在解题思路、思维方式以及求解策略等方面存在较大的差异性。基于该种类型问题的分析及求解，可以对学生问题求解的多样化特征进行剖析，有利于在满足其个性发展的同时，助力其独特思维能力得以順利发展。因此，在平时开展开放题教学过程中要注意切实尊重小学生个体本身的差异性，并且要善于指导学生结合数学题目中的有关条件，自主出题及求解问题，充分运用问题开放题的合理设计来调动小学生主体能动性，有效锻炼及培养其自身的创造性与创新性思维，助力其自身个性得以顺利、自由地发展。

例２：小李爷爷在自家果园中栽植了一些苹果树与梨树，已知苹果树与梨树栽植棵数之比为５∶７，＿＿＿＿＿＿，试求梨树总计栽植的棵数？

解析：该题是一道经典的问题开放题，在指导小学生求解问题期间，首先要对问题中未给出的问题条件进行补充，再进行求解。问题条件补充的不同，相应的求解思路及方法也会存在一定差异，最终求解问题得到的结果也是各不相同的。通过这种类型的开放题设计及实施，可以有效锻炼学生的个性化思维和创造性思维，同时也可以借此来促进其创造力的发展。

解：（１）对问题条件进行补充“已知种植的苹果树是５５棵”，那么此时可知种植的梨树棵数是：５５÷５×７＝７７（棵），或５５÷（５÷７）＝７７（棵），最终顺利求解本道数学题。

（２）对问题条件进行补充“已知种植的苹果树比梨树少１８棵”，那么此时可知种植的梨树棵数是：１８÷（７－５）×７＝６３（棵）。

（３）对问题条件进行补充“已知种植的苹果树和梨树数目总计８４棵”，那么此时可知种植的梨树棵数是：８４÷（７＋５）×７＝４９（棵）。

由此可见，在对问题开放题进行求解期间，如果小学生补充的问题求解条件不同，那么就需要采用差异化的求解方法和求解思路，最终得到的求解结果也会有所差异。但是无论学生补充了何种解决问题的条件，最终都可以对他们的个性化思维以及创造性思维等进行有效锻炼，使其整体思维能力得以有效锻炼及发展。

（三）巧设结论开放题，开展思维培养

结论开放题主要是给出确定的解题条件，但是没有给出确定结论的一类数学问题，即数学问题求解过程中涉及的求解思路及方法各不相同，且最终的解题根本目标是促进学生创造性、创新性和个性化思维的全面发展。针对结论开放题的求解，主要是指导小学生结合题干给出的解题信息，从多维度进行思考，保证最终获得合理、准确的解题结果。

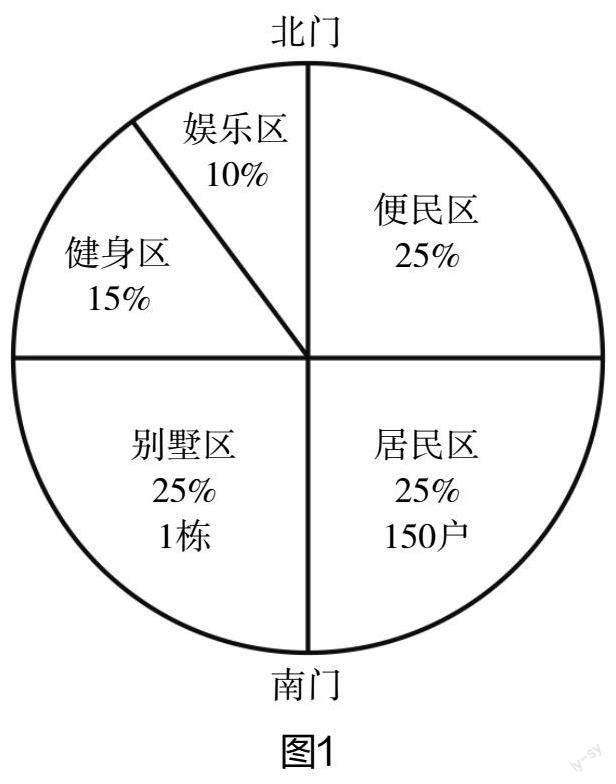
例３：如图１是某一个住宅小区的构成图，南门和北门之间直线距离为１６０ｍ，并且划分成了众多功能分区，试求：①本小区总计占地面积为多少？②小明每天在小区外侧会进行慢跑，每天跑５圈，试求小明每天会慢跑多长距离？③住宅小区物业公司为了响应“垃圾不落地，构建魅力社区”的号召，在小区内部推行了“垃圾分类”活动，现在想要在小区中建造一个“社区环保屋”，那么你觉得应该修建在小区的哪个位置呢？试用△进行标注，并说一说自己的理由？

解析：针对本道结论开放题的求解，学生根据题干信息可以快速意识到本道题实际上就是“圆的周长和面积”方面的知识的应用。针对问题①和问题②的求解，学生只需要结合题干给出的南北门直线距离是１６０ｍ来确定这个圆的半径是８０ｍ，之后可以直接代入圆的面积和周长计算公式来进行快速计算。而针对本道结论开放题的问题③，学生在进行求解的过程中需要综合考虑多方面的因素，如各功能区域的人数以及垃圾杂物产生量，垃圾投递便捷性和安全性等，所以本道题的正确答案可能并不是唯一确定的，只要是学生结合自己的学习情况给出了自己的看法，那么就应该及时进行鼓励和表扬，切不可利用“一刀切”的答案设计方式影响部分小学生学习的积极性，否则也会直接限制其个性发展和创新性思维能力发展。

（四）巧设综合开放题，开展思维培养

除上述几种类型的开放题外，综合开放题也是比较多见的开放题，主要是对给定数学问题中的条件、方法、結论等进行调整来设置综合性开放问题，借此来对小学生综合运用数学知识的能力进行考查。在对该种类型的数学开放题进行设计的过程中，主要的设计出发点是突出及强化“综合”这一特征，即引导全体小学生多方位、多角度开展深入思考活动，并在指导他们对问题进行分析及求解的过程中来锻炼其自身的思维能力。

例４：在放寒假前，小红和她的一些小伙伴打算出去游玩几天，现在已经获得了她们家长的同意，并且给了她们１５００元旅游费用，但是规定时间不能超过３天，回到家的时间也不能够超过晚上７点，试帮助她们设计一份最佳的旅游出行计划。

解析：本道开放题的设计初衷是对学生的综合能力进行有效锻炼，但是为了保证最终顺利设计出一份绝佳的出游计划，可以指导学生亲自动手查询自出发点到旅游点的轮船、公交车等多种交通工具的票价及时刻表等，明确相关旅游景点的门票价格以及其他关键的旅游信息，将这些知识与学生的生活实际进行有机结合，借助这种开放题设计方式可以在巩固学生所学数学知识的同时，对他们的思维进行激活，不仅可以促进其创造性思维的发展，还可以全面锻炼及发展其信息搜集、剖析、归纳及筛选等能力。因为在求解本道综合开放题过程中，不仅需要学生调用以往数学学习过程中的相关知识内容，还需要有计划地应用自身的数学知识综合运用能力。比如有的学生会在选择自己感兴趣的旅游景点基础上，继续有序地对相关的出行时间进行考虑，借助这种有序分析的思维运用方式，可以很好地锻炼学生的逻辑思维、创造性思维以及其他一些高阶思维能力，最终可以全面促进其自身数学综合素质发展，助力其数学核心素养的顺利养成。

总之，思维培养是新课程理念下培养学生数学核心素养的一个根本要务，会对学生数学综合素质发展产生极大影响。而开放题设计及实施是锻炼学生思维能力发展的一个重要路径，所以在实际的数学开放题设计中可以结合学生的思维培养目标，灵活地设计条件开放题、问题开放题、结论开放题以及综合开放题等不同类型的开放题，借助开放题的有效设计及教学指导助力学生思维能力得以发展。

参考文献：

［１］杨宁，满长江． 浅析构建小学数学开放式课堂的策略研究［Ｊ］． 科幻画报，２０２１（０９）：７９－８０．

［２］陶玲俐． 小学数学开放式教学法的应用策略［Ｊ］． 试题与研究，２０２１（２３）：１７－１８．

［3］郝海平． 小学数学开放题研究再思考［Ｊ］． 新课程研究，２０１９，５１５（１５）：１２－１３．

（责任编辑：邹宇铭）