初中数学教学中如何培养学生的探究能力
2023-06-07许良乾
许良乾
【摘要】数学作为初中阶段最为关键的课程之一,数学教师不但要使学生了解最基本的数学知识,还要注重其探索意识的养成与提高.在这一背景下,要切实调动学生的探究兴趣、探究能力,提高他们的探索意识.本文以等腰三角形教学为例,提出从课前导入、问题启发、课堂活动、辨析验证以及分析总结五个层面对学生进行培养的有效策略,以期为相关教育人员提供借鉴参考.
【关键词】初中数学;探究意识;培养途径
《义务教育初中数学课程标准(2022年修订版)》(以下简称《标准》)中对初中数学教学提出了新的要求,其中强调教师要以实际学情为基础,重视启发式教学,要引导学生独立思考、主動探索,让学生在自我提升中培养数学知识与技能,并具备相应的数学思想和相关经验.所以在教学过程中,教师应该全面创新教学活动,充分发挥学生的积极性和主动性,以兴趣为基础,以探究能力为目标,以创新教育方法为途径,全面推进初中生探究能力的培养,以促进学生综合能力的全面发展.
1 情境导入,激发学生的探究意识
课程导入是培养学生学习兴趣、集中学生注意力的关键环节,所以教师需要对课前导入进行充分利用,以调动学生的兴趣,使学生在兴趣的驱使下激发主动探索意识,为其探究能力的培养奠定基础.等腰三角形是初中数学中的重要知识内容,不仅知识点多,而且与其他章节也有一定的关联性,教师应该重视学生的学习状态,并引导学生以饱满的心态和活泼的课堂气氛进入课堂学习之中,以便更有效地提升课堂教学效果.
例如 以“等腰三角形”的知识内容为例,对于该章节而言,等腰三角形的性质和判定是学习其他知识内容的基础和依据,但是性质类的教学内容又多以文字为主,仅凭抽象的讲解,不仅使学生难以理解知识内容,影响记忆效果,更让学生对该章节的内容产生枯燥无趣的印象.情境导入法的应用能够完美解决这一问题.在具体的学习过程中,教师准备好道具:A4纸、剪刀、直尺,用提示性语言引起学生的注意力,如:同学们,老师可以不用测量就能制作出等腰三角形,你们想不想知道老师是怎么做的?学生的注意力被教师吸引,此时教师可以展示制作过程,将白纸对折,然后沿一角剪下,得到一个三角形之后,让学生进行测量,学生通过教师的引导,实际测量得出教师制作的确实是等腰三角形.教师继续引导,同学们,你们知道这是什么原理吗?此时学生会在心中产生疑问“为什么这样剪出来的三角形是等腰三角形?”学生的好奇心被充分调动,进而增强学生能力.
2 问题启发,培养学生的问题意识
问题意识是探究能力训练的根本基础,在教学活动中,通过问题的引导,可以有效调动学生的积极性与探索能力,在寻找答案的过程中,完成对探究能力的培养,是初中阶段有效提升教学效果的重要途径.在实际的教学过程中,教师利用问题引导,层层深入,循序渐进的方式指导学生进行研究,以充分调动学生的积极性,并感受到解决问题之后获得的成就感和喜悦之情,从而有效提高学生的探究意识和探究能力.
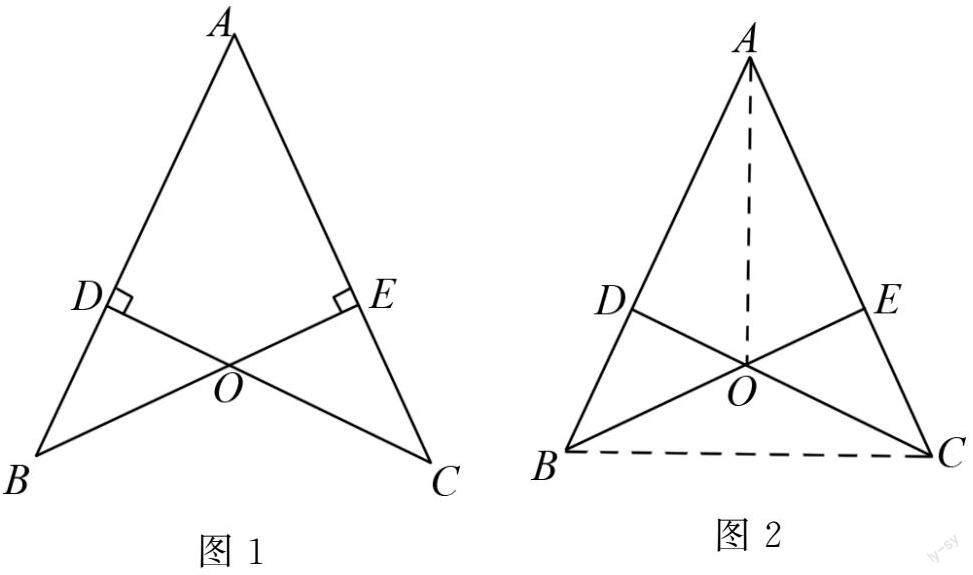
例如 以等腰三角形的相关习题为例,如图1所示,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,以此为条件,求证AD=AE.
在解题的过程中,教师可以以问题方式引导学生,如题中已知的条件是什么?通过教师的提示,学生画出题中的具体条件,由AB=AC可以联想到哪些知识内容?想要得到AD=AE的结论,需要首先得到什么样的条件?结合教师的问题提示,学生开始证明过程:在△ACD与△ABE中,两个三角形共用一个∠A,并且通过已知条件得出,∠ADC=∠AEB=90°,且AB=AC,所以△ACD≌△ABE.所以AD=AE.解题过程结合了全等三角形的性质和判定定理,学生通过教师的问题引导能够一步步得出结论,用问题方式培养逻辑思维,是提高学生探究能力的关键.教师为了更深一步地强化学生对知识点的掌握,可以继续更深入地提问:连接OA,BC,如图2,试判断直线OA,BC的关系并说明理由.
这一问题是对该例题的深化,在Rt△ADO与Rt△AEO中,已经证明得出AD=AE,所以△ADO≌△AEO.所以∠DAO=∠EAO,即OA是∠BAC的平分线.又因为AB=AC,所以OA⊥BC,所以得出结论二者是互相垂直的关系.学生在解题过程中需要进行自主探究和思考,什么条件能够得出什么结论,并且能够全面地掌握等腰三角形的相关知识点,从而有效掌握解题思路和方法,学生的探究能力也可以得到有效的提升.
3 课堂活动,给予学生充足的空间
学生通过教师的讲解获取知识内容和技能方法,失去了独立思考和自主探究的空间,在面对问题时,学生只会结合教师讲解的方法和内容进行套用,而遇到需要转化的拓展问题时,学生就会变得束手无策,阻碍其思维能力的发展.结合《标准》中的教学要求,教师需要利用课堂活动,赋予学生充分的探索余地,以激励、指导的形式引导他们对知识内涵加以探索、总结,针对他们在探索活动中解决不了的难题,教师再给予一定的指导.
例如 在学习等腰三角形的知识内容时,教师可以设计讨论类的活动问题,让学生以讨论的形式,对知识点进行学习和总结,以此达到锻炼学生探究能力的目的.比如,当三角形的腰长或者底边长不确定时,需要让学生对相关问题进行分类讨论:(1)现有条件已知等腰三角形的两条边长为8cm和10cm,求等腰三角形的周长;(2)等腰三角形一条边长为3cm,另一条边长为7cm,求该三角形的周长.这类题目具有一定的开放性,想要求周长就需要确定三条边的长度,但是已知条件只有两条边的长度,所以需要学生讨论到底哪一条是三角形的底边,哪一条是三角形的腰,还要保证三条线段能够构成三角形.所以,在解答时,就需要结合等腰三角形以及三角形的性质进行讨论:第一问中的已知条件,结合三角形的性质,因为8+8>10,10+10>8,所以这两种情况都能构成三角形,通过分类,可以得出:当腰长为8cm时,三角形的周长为8+8+10=26cm;而当腰长为10cm时,三角形的周长为10+10+8=28cm.而在解答第二个问题时,会发现如果腰长为3cm,则3+3<7,这一情况下是不能构成三角形的,所以只有当腰长为7cm时,7+7>3,才能构成三角形,而此时等腰三角形的周长为7+7+3=17cm.这种分类式的练习题能够给学生足够的思考空间,让学生利用三角形的三边关系和等腰三角形的特性进行解答,既能巩固基础知识,又能拓展学生的思维能力,是培养学生探究能力的重要途径.
4 辨析验证,提高学生实践的能力
初中数学的知识内容具有很强的实践性和应用性,在培养学生探究能力的过程中,教师应该注意结合数学知识的特点,通过系统的辨析验证过程,培养学生的实践能力,同时在实践过程中激发学生的探究意识,并促进学生探究能力的培养和提升.
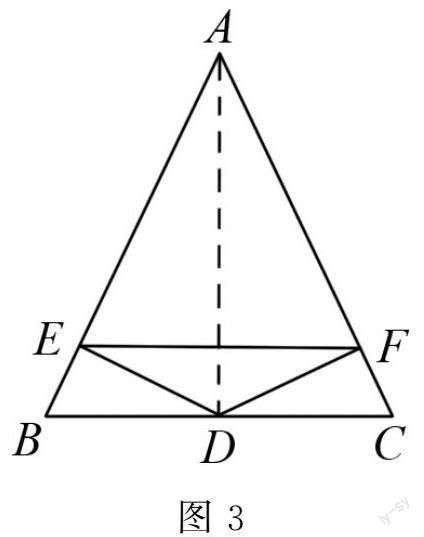
例如 在等腰三角形知識内容的学习过程中,教师可以带领学生进行知识点的辨析验证,让学生将自己的解题思路与教师的解题思路进行对比,并反思自己解题过程中存在的问题,让学生能够在实践过程中掌握解题思路,从而有效提高探究能力.以等腰三角形的练习题为例:如图3所示,已知在△ABC中,AB与AC长度相等,D为BC的中点,且DE⊥AB,DF⊥AC,求证∠DEF=∠DFE.
解题时,教师可以让学生先进行自主解题,等学生们完成之后,教师再进行系统的讲解:首先连接AD,因为AB=AC,D是BC的中点,所以AD平分∠BAC,因为DE⊥AB,DF⊥AC,所以DE=DF,所以∠DEF=∠DFE.让学生将自己的解题过程与教师展示的解题过程进行对比讨论,使学生认识到自己的不足并掌握解题思路,能够有效提高学生的实践能力和对知识点的应用能力,进而实现探究能力的提升.
5 分析总结,完善学生的探究方法
在完成教学内容之后,教师需要对课堂知识点进行梳理,帮助学生回顾整节课的重点和难点知识,而学生通过教师对知识点的梳理,能够发现数学知识点之间的关联性,起到触类旁通、举一反三的效果.
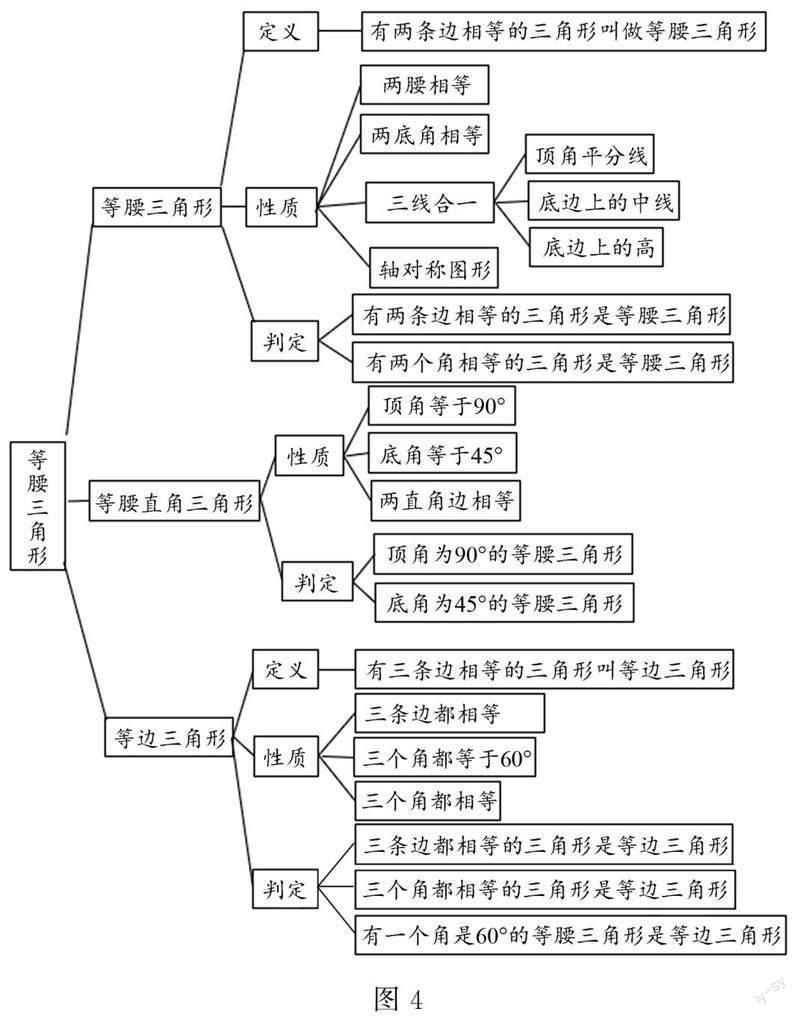
例如 在学习等腰三角形的知识内容时,教师可以在课程结束后,利用思维导图的形式帮助学生对知识内容进行汇总和延伸,如图4所示.
学生通过掌握这一方法,能够自行对知识点进行全面的梳理,一方面能够扎实地掌握知识内容,另一方面通过梳理学会得心应手地解决问题,让学生掌握自主探究的方法,从而有效提升自主探究能力.
6 结语
总而言之,数学是学生实现全面发展的基础知识,良好的探究能力关系着学生的学习能力和学习效率.教师应该深入分析《标准》中的相关要求和教育原则,重视学生的兴趣培养,利用学生的好奇心和自信心引领学生实现探究能力的提升.在课堂教学活动中,明确自身的作用,坚持启发性和引导性的原则,让学生在自主探究的过程中自由地遨游在数学知识的海洋中,全面提高学生的探究能力,为学生综合素质的全面提升保驾护航.
参考文献:
[1]胡丽梅.探究如何在初中数学教学中培养学生的探究能力[J].天天爱科学(教育前沿),2020(11):120.
[2]高连德.在初中数学教学中如何培养学生的探究能力[J].新课程教学(电子版),2018(08):98.
[3]汪卫.核心素养视角下初中数学探究式教学——以“等腰三角形性质”教学为例[J].数学学习与研究, 2019(9):1.
[4]张立志.浅谈初中数学教学中如何培养学生的探究能力[J].新课程(中学),2016(01):233.
[5]沙雯艳.在等腰三角形教学中加强对学生探究能力培养的策略[J].试题与研究(教学论坛),2020(2):1.
