高中数学核心素养背景下学生直观想象能力的培养策略

辛艳

数学是一门研究数量关系与空间几何形式的学科。为了让学生更清晰、深刻地把握数学学科的核心本质，得到数学核心素养的发展，本文立足核心素养教育背景，聚焦学生直观想象能力的培养，探讨了高中数学教学中有效培养学生直观想象能力的策略，旨在对学生直观想象能力进行针对性培养，进一步促进核心素养育人目标的落地，让学生通过对数与形的全面观察和深入探究提升思维品质，感知数学学科别具一格之美。

一、提供清晰表象，促进思维加工

直观想象能力强调的是学生对几何直观图形与空间想象的利用。由此，高中数学教师以核心素养为导向培养学生直观想象能力时，便可直截了当地为学生提供空间几何图形，让学生结合清晰的表象展开思维加工与头脑风暴，进而为其直观想象能力的形成夯实基础。

例如，在教学人教版高中数学必修第二册（A版）“空间点、直线、平面之间的位置关系”一课时，高中数学教师就可以在学生了解平面及其基本性质后，从学生的已知入手，为学生提供常见且熟悉的空间几何图形“长方体”，让其以长方体为支点探究空间内点、直线、平面的位置关系。

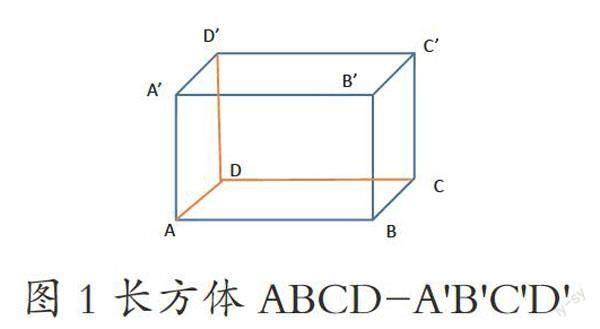
首先，在希沃白板中为学生直观绘制一个长方体ABCD-A'B'C'D'（如图1所示），并提出问题“长方体有怎样的结构特征？有几个顶点？几条棱？几个面？长方体ABCD-A'B'C'D'中的几个顶点、几条棱、几个面之间存在怎样的位置关系？”驱动学生细致观察几何图形，探究空间中点与直线、与平面的位置关系。

空间中点与直线的位置关系有两种：即点在直线上与点在直線外，如点A在直线AB上，点A在直线A'B'外；空间中点与平面的位置关系也有两种：即点在平面内与点在平面外，如点A在平面AA'BB'内，点A在平面CC'DD'外。

其次，引导学生围绕长方体ABCD-A'B'C'D'探究空间中直线与直线、直线与平面的位置关系。

【空间内直线与直线的位置关系】观察图1可以发现空间中直线与直线之间的位置关系共有三种：一是互为平行直线，如直线AB与直线CD在同一平面ABCD内，没有公共点，二者为平行线，记作AB∥CD；二是相交直线，如直线CD与直线DD'在同一平面CC'DD'内，有公共点D，二者为相交线，记作CD∩DD'=D；三是不在同一平面内的两条直线，如直线BC与直线A'D'不在同一平面内。

学生根据图1长方体ABCD-A'B'C'D'自主总结归纳出以上空间内直线与直线的三种位置关系后，数学教师就可以引导学生以“异面直线”与“共面直线”两种数学概念对空间内直线位置关系进行分类（如图2所示），以更好地厘清学生的数学思路，避免认知混淆、记忆错乱等影响学习效率问题的出现。

【空间内直线与平面的位置关系】通过对空间内直线位置关系的探究与对长方体ABCD-A'B'C'D'的细致观察，学生便会迅速地做出回答：空间内直线与平面的位置关系共有三种：一是直线在平面内，如直线AB在平面ABCD内，有无数个公共点；二是直线与平面相交，如直线AB与平面AA'DD'相交，有且仅有一个公共点A；三是直线与平面平行，如直线AB与平面CC'DD'平行，没有公共点。

最后，利用多媒体将长方体ABCD-A'B'C'D'抽象为学生所在的教室空间，让学生结合生活实例分析与探究空间内平面与平面的位置关系。可将长方体ABCD-A'B'C'D'的六个面AA'DD'、A'B'C'D'、BB'CC'、ABCD、AA'BB'、CC'DD'分别看作教室的黑板所在面、天花板所在面、教室后墙所在面、地板所在面与教室左右墙所在面。由此，便可轻而易举地得出空间内平面与平面的位置关系共有两种：一是两平面平行，没有公共点与公共直线，如黑板所在面“AA'DD'”与教室后墙所在面“BB'CC'”相互平行，没有公共点与公共直线；二是两平面相交，有一条公共直线与无数公共点。如黑板所在面“AA'DD'”与教室天花板所在面“A'B'C'D'”相交，有一条公共直线A'D'，在直线A'D'中任意定点，平面AA'DD'与平面A'B'C'D'便会有无数个公共点。