轨控喷流干扰气动--运动一体化非定常数值模拟

谢信辉，柳煜玮，刘耀峰

(中国航天空气动力技术研究院，北京 100074)

0 引言

大推力喷流控制技术可实现大机动、强突防[1]，在多种飞行器上都有广泛的应用，如低速状态下横流中烟囱羽流[2]和高速状态下飞行器拦截系统[3]。特别是在拦截任务的最后阶段，要求拦截飞行器具有高度的机动性，提供直接作用力、快速响应的侧向喷流控制推进器，这是对传统气动控制面的有效补充。

喷流产生的三维流场是高度复杂的，包含复杂的波系、涡系结构及其相互干扰，呈现高度非定常、非线性、强湍流特性[4]，现阶段对运动条件下非定常效应的研究很少。早在1964年Zukoski等[5]就开展了不同马赫数下声速喷管欠膨胀喷流喷入超声速外流的实验研究，指出了弓形激波、分离激波、分离区等主要特征。随着计算流体力学的发展，CFD技术在喷流干扰流场研究领域得到广泛应用。1991年张涵信等[6]利用NND格式，完成了钝锥完全气体侧喷干扰流场的计算。2005年徐敏等[7]研究了脉冲发动机喷流的非定常性对飞行器控制的关系。

当喷流开启与关闭时，存在强烈的非定常特性，同时伴随飞行器运动与姿态变化，存在气动特性与运动特性的强耦合，为了有效评估飞行性能，须要考虑气动运动耦合带来的非定常问题。关于空气动力学与飞行力学耦合方法的研究，国外近年来发展和应用了大规模模拟的最新数值方法[8-11]。Sahu等[12]在超级计算机上对飞行器的“虚拟飞行”进行了研究，使用耦合的CFD/RBD技术对飞行器的实际飞行轨迹和所有相关的非定常自由飞行空气动力学进行数值预测。Silton等[10]通过与自由飞行实验数据进行比较，完成了对虚拟飞行模拟计算结果的验证。刘耀峰等[1]应用非定常方法数值模拟了侧向喷流干扰流场建立与消退过程。陈坚强等[13]模拟了舵面运动与侧向喷流间耦合干扰问题。以上研究具有丰富的价值，本文的重点是将气动--运动一体化方法应用到喷流干扰问题中，对运动条件对喷流干扰的影响做进一步的探索研究，为工程实践的应用提供参考。

本文基于雷诺平均N-S方程和刚体六自由度运动方程，介绍了将飞行力学方程耦合进CFD解算器的方法，飞行器运动时用到的刚性动网格方法，采用松耦合实现飞行力学方程与流场控制方程的耦合计算，建立非定常气动--运动一体化方法，以及计算方法的验证等。对一种采用轨控喷流直接力控制的锥柱裙外形进行了数值模拟，给出了锥柱裙外形在喷流作用下做轨控运动的非定常计算结果，研究了干扰流场结构、力与力矩和飞行器状态随时间变化特性，并与定常结果进行对比，分析了外流参数变化对气动运动特性的影响。结果表明轨控运动非定常状态流场结构和气动力与定常状态存在差异，工程实践中须要考虑运动非定常效应的影响。

1 数值模拟方法

1.1 流体力学方程

三维可压缩流动N-S方程的量纲为1化形式为

(1)

采用有限体积法，无黏通量使用二阶精度Roe格式[14]进行离散；黏性通量使用中心差分格式；时间推进使用双时间步方法[15]；湍流模型使用一方程S-A湍流模型[16]。为加速收敛、提高计算效率，使用了基于信息传递接口(MPI)的网格分块并行技术。边界条件为壁面无滑移边界，远场考虑网格动态运动边界。

1.2 飞行力学方程

飞行力学平动方程定义在惯性系，它是固定系，如下

(2)

式中，V为线速度，m为质量，F为力。

飞行力学的转动方程定义在体轴系，它是动坐标系，与惯性系相互转换定义姿态角(γ，θ，ψ)，如下

(3)

式中，ω为角速度，I为转动惯量，M为力矩。

对于飞行力学方程，使用显式四阶龙格-库塔方法求解。

1.3 气动--运动耦合方法

耦合方法可分为全耦合、松耦合、紧耦合，考虑到松耦合思路简单，拥有更高的计算效率，本文采用松耦合算法。

松耦合可以使模块之间求解独立，示意图见图1。在n时刻流场信息都是已知量，CFD将力和力矩传给RBD，求解飞行器位移和姿态传给CFD，生成新的网格，求解得到n+1时刻的流场信息，物理时间步向前推进了一步。

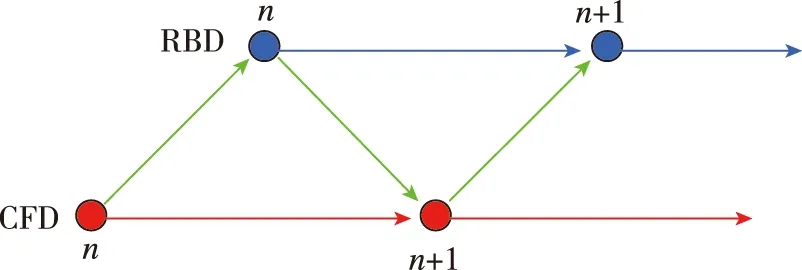
图1 CFD/RBD松耦合Fig.1 CFD and RBD loose coupling

1.4 刚性动网格方法

刚性动网格是最简单有效的网格变形技术，适用于任意幅度的运动，网格按照飞行器的运动而一起运动，根据平动位移和转动角度直接给出变形之后的网格坐标，网格速度被指定给每个网格点。

1.5 数值方法验证

本节验证了亚声速和超声速条件下两个算例。一是76°后掠平板三角翼模型在Ma=0.3下，绕2/3转轴做从0°攻角上仰至 90°攻角的俯仰线性运动，攻角变化公式为

α=kt

(4)

式中，k为减缩频率，取0.024。图2给出了升力系数随攻角变化曲线，与文献[17]结果相比，随着攻角增大，升力系数先增大后减小，峰值与风洞实验结果吻合。

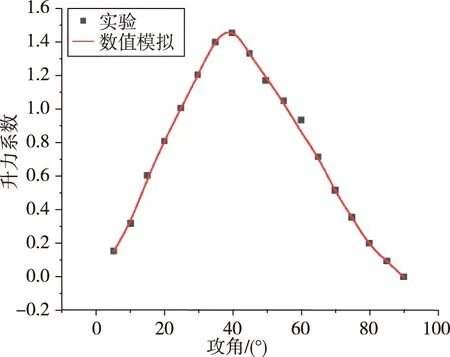
图2 升力系数变化曲线Fig.2 Variation curves of lift coefficient

二是标模Finner在Ma=2.5下，模拟的是无初始角速度情况下，喷流在t=0时开启，作用时间20 ms，然后关闭的周期振荡运动。图3给出了攻角随时间变化曲线，幅值随着时间增加而减小，与文献[18]结果吻合较好。

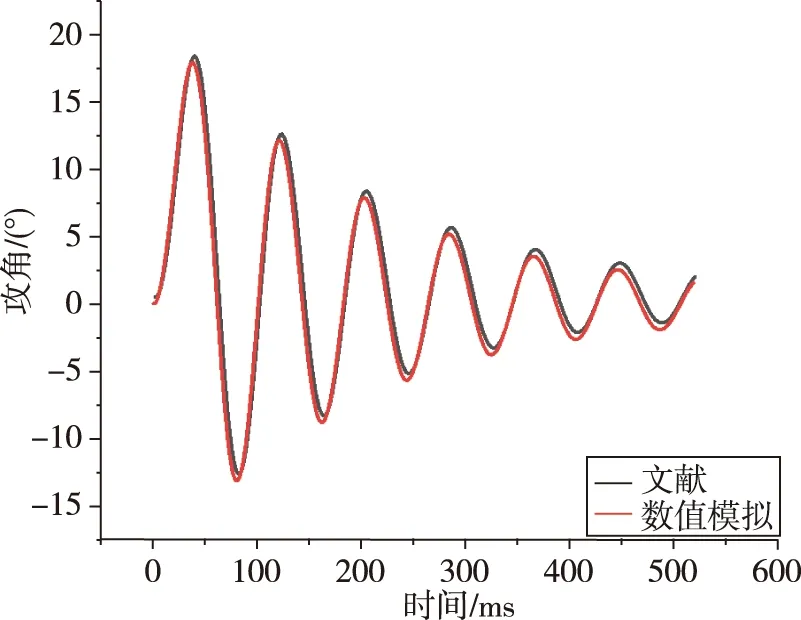
图3 攻角变化曲线Fig.3 Variation curves of angle of attack

2 计算模型和计算条件

计算模型是锥柱裙外形模型，如图4所示。模型总长2 250 mm，坐标原点O位于飞行器头部顶点，x表示横向，y表示纵向，轨控喷流中心位于x=1 177 mm 质心处。整体计算网格为C-H型，采用分区对接方式，在物理量变化剧烈处加密，网格总数为146万。图5给出了网格整体布局。

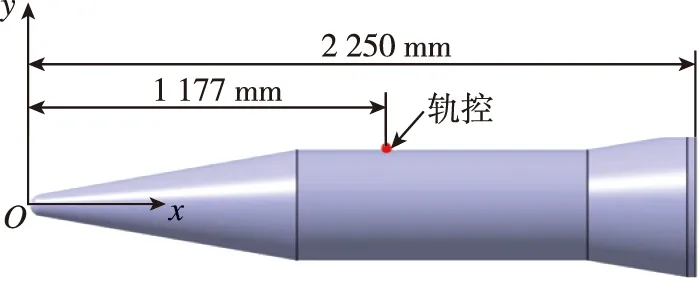
图4 锥柱裙外形模型Fig.4 Cone-cylinder-flare model

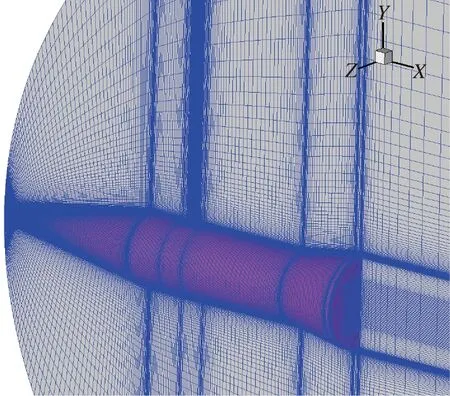
图5 网格布局Fig.5 Grids of model

计算状态为：马赫数为6，高度为20 km，攻角为0°，喷口中心位于飞行器下表面的质心处。来流条件、喷流条件和飞行器参数分别见表1、表2和表3。

表1 来流条件Tab.1 Air conditions

表2 喷流条件Tab.2 Jet conditions

表3 飞行器参数Tab.3 Aircraft parameters

3 结果与分析

3.1 轨控运动干扰流场发展历程

图6给出了H=20 km喷流使飞行器轨控运动的压力云图，图中反映出了干扰流场细节随时间变化的特征。t=0 ms时，流场呈现上下对称状态，头部有一道弓形激波，在飞行器尾部形成涡流；t=10 ms时当喷流垂直射入超声速来流，就像是形成一道障碍，在喷流前方产生一道很强的弓形激波，喷流反作用推动飞行器向上爬升；t=50 ms 时，在喷流产生的干扰俯仰力矩的作用下有约1°抬头，喷流干扰区由下表面向上表面覆盖，喷口前高压影响范围扩展到了上表面，产生了包裹效应，造成了总体喷流干扰力的降低。

图7给出了不同攻角下下表面180°子午线上压力分布比较图，压力分布的不同主要集中在3个区域：飞行器前方锥段(区域1)、喷流出口前方高压区段(区域2)和飞行器后方尾裙段(区域3)。随着飞行器运动向上抬头，攻角增大，锥段压力增大，喷流前方压力增大，尾裙段压力减小。

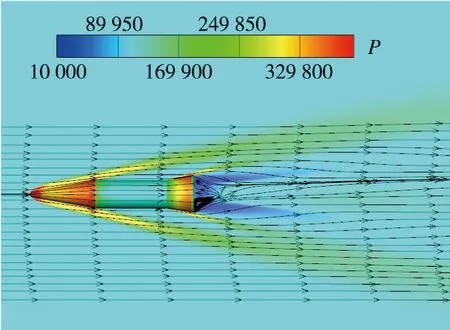
(a)t=0 ms

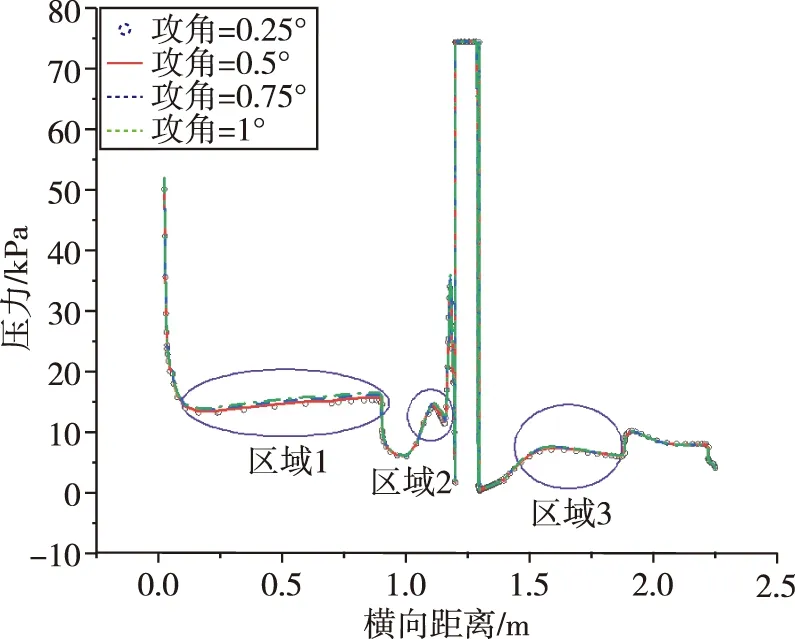
图7 不同攻角下下表面180°子午线上压力分布比较图Fig.7 Pressure distribution of 180° centerline at different angle of attack

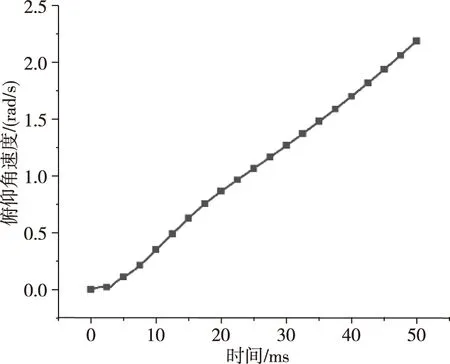
(a)俯仰角速度

3.2 运动状态和气动系数随时间变化特性

图8分别给出了飞行器俯仰角速度和俯仰角随时间变化曲线，喷流的持续作用使飞行器各个运动状态随时间增大。图8(a)显示俯仰角速度跟时间近似成线性关系，图8(b)显示在喷流开启50 ms后飞行器产生了1°左右的抬头。

图9给出法向力系数和俯仰力矩系数随时间变化曲线，包括总气动力和力矩系数、喷流本身产生的气动力和力矩系数和固壁表面除喷流其他区域的气动力和力矩系数。对于法向力系数，在20 km下，随着飞行器抬头，总法向力随时间推进增大，喷流本身推力基本保持不变；对于俯仰力矩系数，喷流开启时俯仰力矩变化剧烈，而后随着飞行器抬头，总俯仰力矩随着俯仰角的增大而增大，并且增大的越来越快，喷流本身产生的力矩基本保持不变。

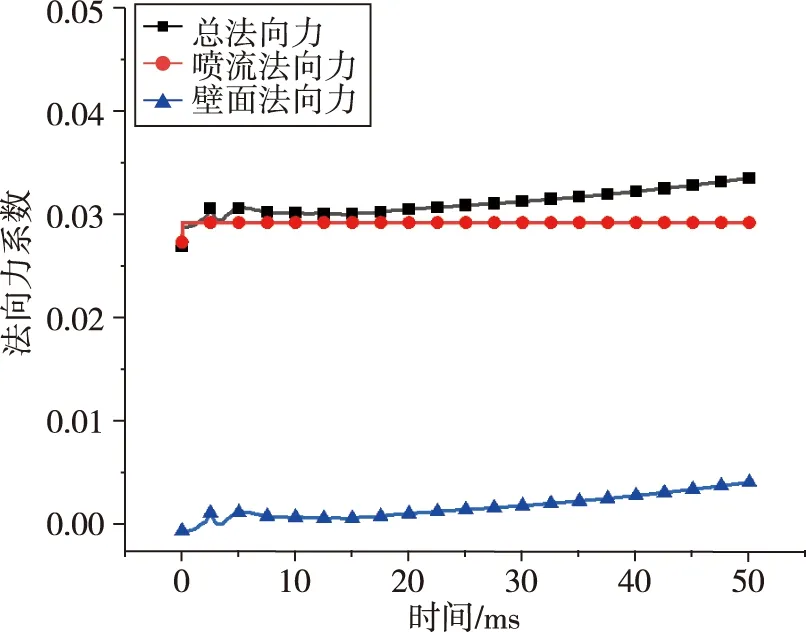
(a)法向力系数

3.3 运动非定常与定常结果对比

为了考量气动--运动耦合效应带来的影响，从两大方面进行运动非定常状态和定常状态的比较，一是流场结构，包括表面极限流线图、压力云图、分离距离；二是压力分布和力与力矩对比，包括下表面180°子午线上压力分布比较图、法向力放大系数和干扰俯仰力矩。

首先给出运动非定常计算和定常计算表面极限流线图，图10和图11是俯视视角，可以看到运动非定常状态与定常状态相比，表面流线结构非常相似。图12和图13是侧视视角，关注喷口前表面第一道分离线，运动非定常状态的分离线在飞行器表面所包裹的面积比定常状态更大。图14和图15是喷口处左视视角，运动非定常状态的下表面高压区比上表面覆盖的范围更大。定义分离距离为喷管中心到前缘分离线的距离，如图16所示，可以看到运动非定常状态的分离距离在不同俯仰角下是大于定常状态的。

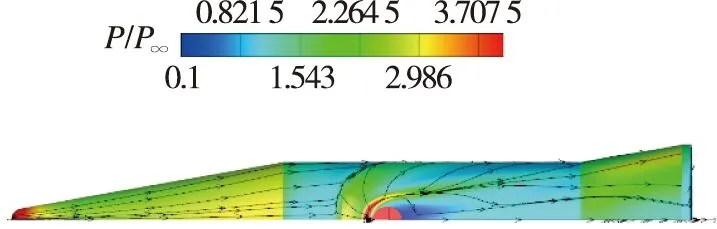
图10 运动非定常θ=1°表面极限流线俯视图Fig.10 Top view of surface limit streamlines of unsteady state at θ=1°

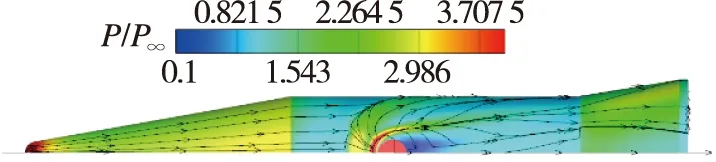
图11 定常θ=1°表面极限流线俯视图Fig.11 Top view of surface limit streamlines of steady state at θ=1°

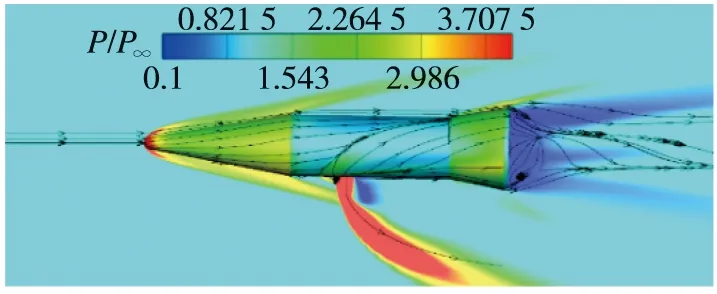
图12 运动非定常θ=1°表面极限流线侧视图Fig.12 Side view of surface limit streamlines of unsteady state at θ=1°

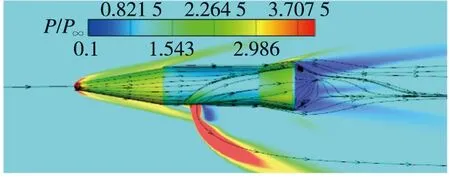
图13 定常θ=1°表面极限流线侧视图Fig.13 Side view of surface limit streamlines of steady state at θ=1°

图14 喷口中心处运动非定常θ=1°压力云图Fig.14 Pressure contours at jet center of unsteady state at θ=1°

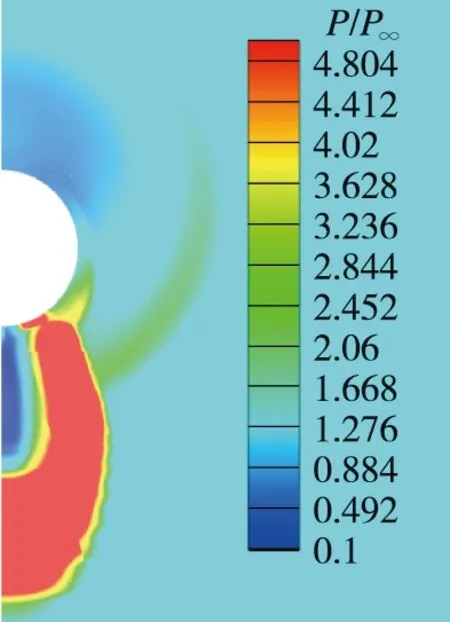
图15 喷口中心处定常θ=1°压力云图Fig.15 Pressure contours at jet center of steady state at θ=1°

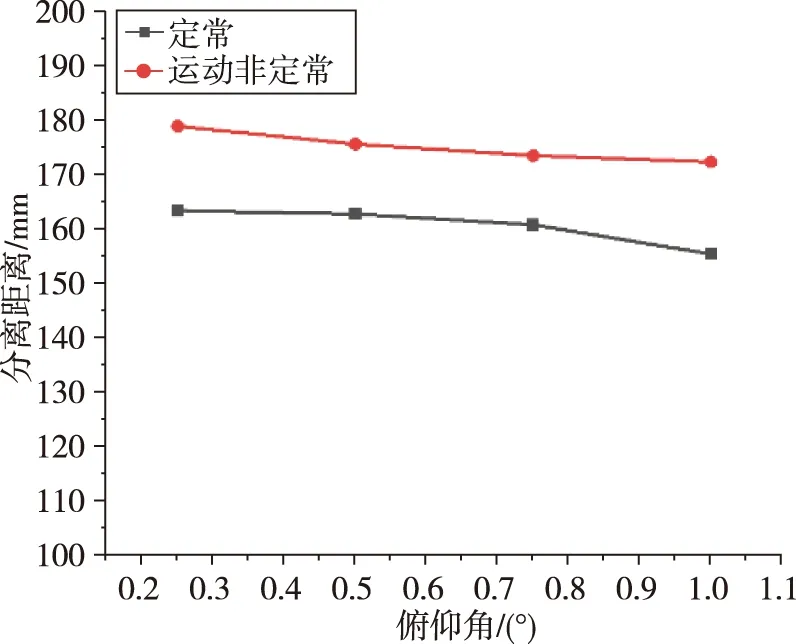
图16 运动非定常与定常状态分离距离对比Fig.16 Separation distance of steady and unsteady state

进一步考察更细致的对称线上的压力分布，图17给出俯仰角为1°时运动非定常状态下表面180°子午线上压力分布与定常状态比较图，可以看出运动使喷口前分离区极值点前移、压力减小，使喷口后尾迹区压力增大，使尾裙上压力减小。

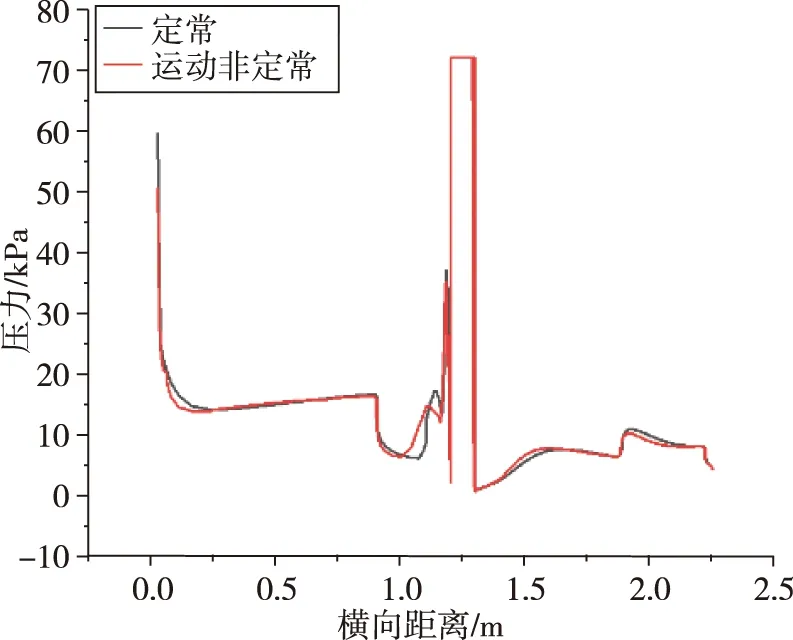
图17 运动非定常与定常状态下θ=1°表面180°子午线上压力分布对比Fig.17 Pressure distribution of 180° centerline between steady and unsteady state at θ=1°

定义法向力放大系数、干扰俯仰力矩，来分析喷流干扰气动特性

(5)

图18给出了定常、不运动非定常和运动非定常状态计算结果的随俯仰角变化曲线对比图。以俯仰角为自变量，定常状态定点计算0°～1°，取间隔0.25°下定常状态的法向力放大系数、干扰俯仰力矩，法向力放大系数随俯仰角的增大而增大，且同一俯仰角下定常状态比运动非定常状态更大。干扰俯仰力矩也随俯仰角的增大而增大，在0.25°时运动非定常和定常状态差别小，而1°时运动非定常和定常状态差别大。这是由于运动非定常状态飞行器的运动速度逐渐增大，非定常迟滞效应增大，流场变化跟不上飞行器运动，形成阻尼作用。为了进一步考察运动特性带来的影响，增加了一组不运动非定常状态的计算结果。由图18中可知，不运动非定常状态的计算结果收敛到定常状态，说明运动带来的额外影响是存在的。

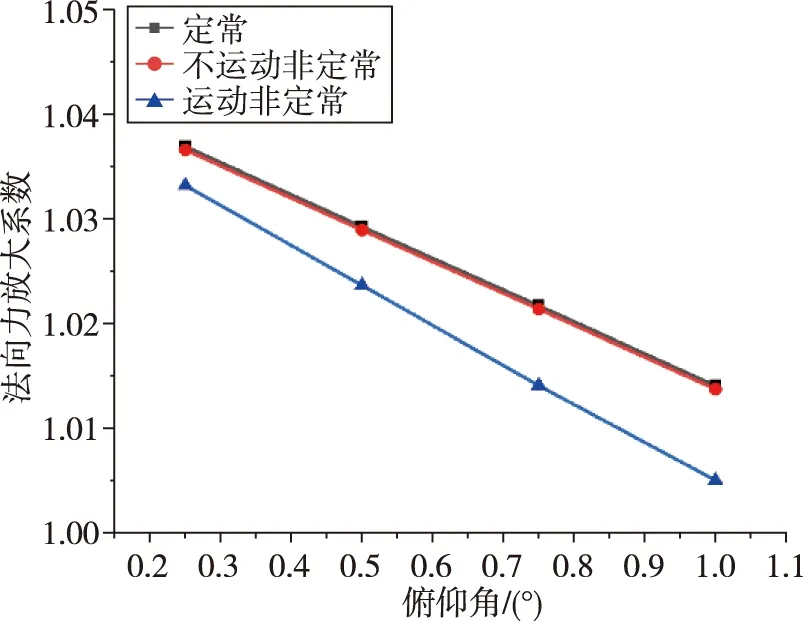
(a)法向力放大系数对比

分析运动非定常与定常状态差异产生的原因，有飞行器运动带来的迟滞效应与喷流干扰两种因素影响。将飞行器分为三段，头部锥段是迟滞效应主要影响区，喷流柱段和尾裙段是喷流主要的影响区域，如图19所示。取图18中θ=1°的一组状态，表4和表5分别给出了此时运动非定常与定常状态的法向力和俯仰力矩的差值在飞行器三段的占比。头部锥段差异占比分别为56.2%和80.0%，是主要部分，反映气动流场的迟滞效应是引起运动非定常与定常状态结果差异的主要原因，喷流柱段和尾裙段差异占比更少。

表4 运动非定常与定常状态法向力在θ=1°差异占比Tab.4 The difference ratio of the normal force between the unsteady and stady state at θ=1°

表5 运动非定常与定常状态俯仰力矩在θ=1°差异占比Tab.5 The difference ratio of the pitching moment between the unsteady and stady state at θ=1°

图19 飞行器三段示意图Fig.19 Three parts of aircraft

为了将迟滞效应与喷流干扰隔开对比，进行了一组无喷强迫俯仰振荡计算，运动方程为

θ(t)=θ0+θmsin(kt)

(6)

其中，θ0为初始俯仰角，设为0；θm为振幅，取值2°；k为角频率，取值10π。图20给出了非定常力与力矩系数迟滞曲线与定常状态对比，法向力系数和俯仰力矩系数始终围绕静态数据，存在迟滞。向上俯仰时，它不如定常状态；向下俯仰时则相反。同样，表6和表7分别给出了飞行器在θ=1°时运动非定常与定常状态的法向力和俯仰力矩的差值在飞行器三段的占比，可以看到，无喷流干扰时，头部锥段差异占比分别为67.8%和88.4%，比有喷时占比更大，此时迟滞效应更显著。

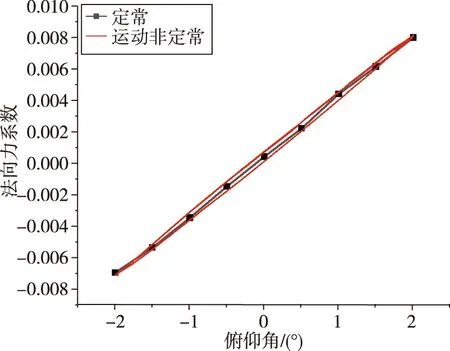
(a)法向力系数对比

表6 运动非定常与定常状态法向力在θ=1°差异占比Tab.6 The difference ratio of the normal force between the unsteady and the stationary state at θ=1°

表7 运动非定常与定常状态俯仰力矩在θ=1°差异占比Tab.7 The difference ratio of the pitching moment between the unsteady and the stationary state at θ=1°

对于迟滞效应，可以从数学分析上进行解释，如图21所示。来流速度为U∞，攻角为α，当飞行器做俯仰运动以w的角速度向下旋转，前缘处会有一个V的向下速度，此时前缘的实际速度只有Vreal=U∞sinα-V，实际攻角被减小，达到真实攻角α的时间被延迟了。

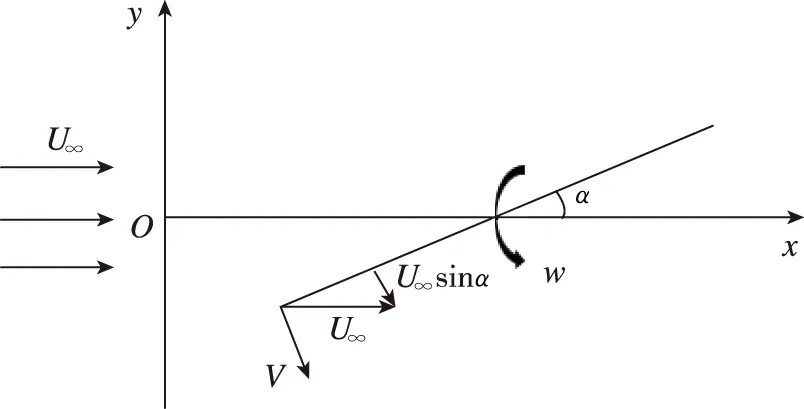
图21 飞行器俯仰运动Fig.21 Aircraft pitching motion

3.4 来流参数的影响

本节关注不同来流马赫数、飞行高度和初始攻角对喷流干扰非定常效应的影响。以表1的来流条件作为对照组，分别改变马赫数Ma=6，7，8，高度H=20，25，30 km，初始攻角α0=-2°，0°，2°，对比分析了不同来流条件对运动状态的响应。由图22～图24可以得出：俯仰角因马赫数不同而产生不同的变化趋势，在Ma=6时飞行器抬头，产生正俯仰角；而Ma=8时飞行器却低头，产生负俯仰角。因高度不同，动压不同，俯仰角增大的幅度不同，高度越高，俯仰角变化越小。俯仰角变化跟初始攻角成非线性关系，计算到50 ms 时，α0=2°时俯仰角变化更大。

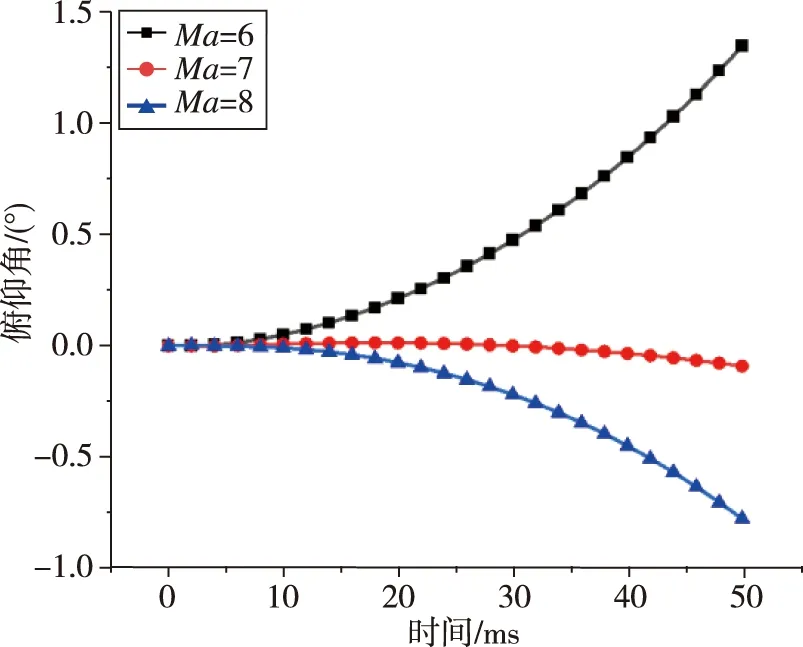
图22 不同马赫数下俯仰角比较图Fig.22 Variation curves of pitching angle at different Mach numbers

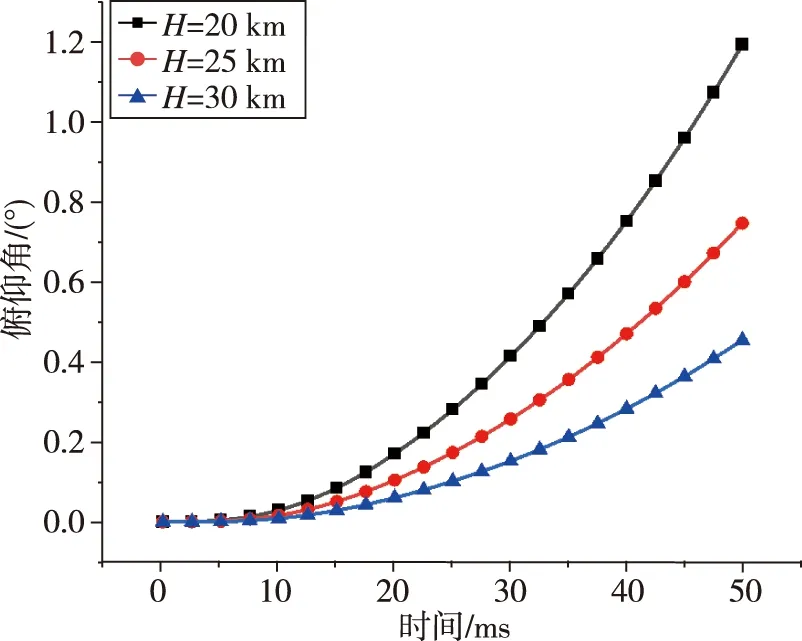
图23 不同高度下俯仰角比较图Fig.23 Variation curves of pitching angle at different altitudes

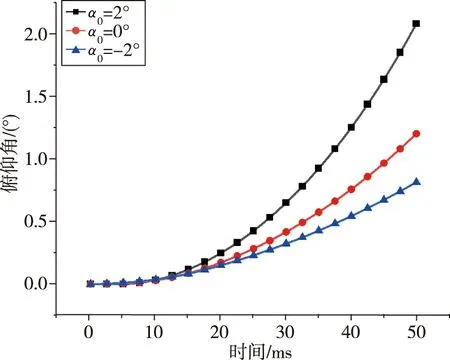
图24 不同初始攻角下俯仰角比较图Fig.24 Variation curves of pitching angle at different initial attack angles

4 结论

针对现阶段对运动条件下的喷流干扰非定常效应研究很少的问题开展研究，建立非定常气动--运动一体化方法，验证了方法的正确性，数值模拟了锥柱裙外形轨控运动非定常效应，研究了干扰流场结构、力与力矩和飞行器状态随时间变化特性，对比了运动非定常计算和定常计算的结果，分析了外流参数变化对气动运动特性的影响。得到如下结论：

1)飞行器运动条件下轨控喷流气动干扰存在强烈的非定常和非线性特性。

2)运动使喷口前分离区极值点压力减小，分离距离有所增大。

3)法向力放大系数和干扰俯仰力矩定常计算的结果高于运动非定常计算结果，原因是存在非定常迟滞效应，流场变化跟不上飞行器运动。

4)改变来流马赫数会影响俯仰角变化趋势，高度越高，俯仰角变化越小，俯仰角变化跟初始攻角成非线性关系。

本文给出了运动条件对轨控喷流控制气动干扰的影响，并得到了一些有意义的结论。为了满足工程实践中精度要求，使数值模拟结果更逼近真实飞行，须要考虑这种影响，以便反映更真实的物理现象。