点目标假设下的二维精度体系研究
2023-06-05白文露
王 智,王 鹏,何 磊,白文露,夏 川
(北京宇航系统工程研究所,北京 100076)
0 引言
飞行器落点散布由一系列彼此独立的随机干扰因素引起。虽无法事先确定每种干扰因素的具体数值,但其均符合一定的统计特性。按照概率论中心极限定理[1-3]:对于大量随机变量之和,如果每个随机变量对总和的作用是微小的,且彼此不相关,则此和式近似于正态分布。因此,可以认为落点偏差的概率分布遵循正态分布规律。
在点目标假设下,表征飞行器二维精度的常用指标是均方根误差和圆概率偏差。在不同的应用场景,二维精度指标需用概率偏差表示。
本文在点目标的假设下,应用概率论正态分布理论,在二维圆概率偏差线性公式的基础上,给出了基于纵横向均方根误差分段的圆概率偏差精确公式,同时对二维精度指标体系及相互转换关系进行了研究。
1 落点散布坐标系
要描述飞行器落点C围绕目标点T的分布,须要明确落点偏差量的表示方法,规定落点散布平面为目标点T处的水平面,以T为原点Oc,用发射点O矢径ro与目标点T矢径rt所组成的平面与散布平面的截线顺飞行方向为ΔL轴,即纵向,从O点指向T点的方向为正;在散布平面内与T点相垂直的方向为ΔH轴,即横向,指向ΔL轴右方为正。飞行器落点C在落点散布坐标系Oc-ΔLΔH中的ΔL,ΔH即为纵向落点偏差和横向落点偏差,如图1所示。
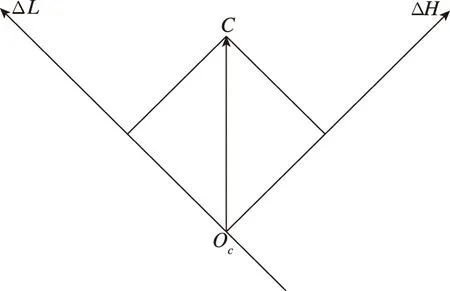
图1 落点散布坐标系示意图Fig.1 Schematic diagram of falling point dispersion coordinate system
2 二维精度指标体系及相互关系
2.1 均方根误差
若瞄准点为目标中心,则其纵向ΔL、横向ΔH分布规律的二维正态分布为
(1)
式中,μΔL,μΔH为系统性偏差;σΔL,σΔH为随机误差和均方根误差;ρ为纵横向相关系数,0≤ρ<1。
考虑没有系统性误差,即μΔL=μΔH=0,并且纵横向独立,则(ΔL,ΔH)的密度函数分别为
(2)
(3)
假定σΔL=σΔH=σ,即落点为圆散布,此时有
(4)
ΔL和ΔH的联合概率密度函数分布如图2所示。
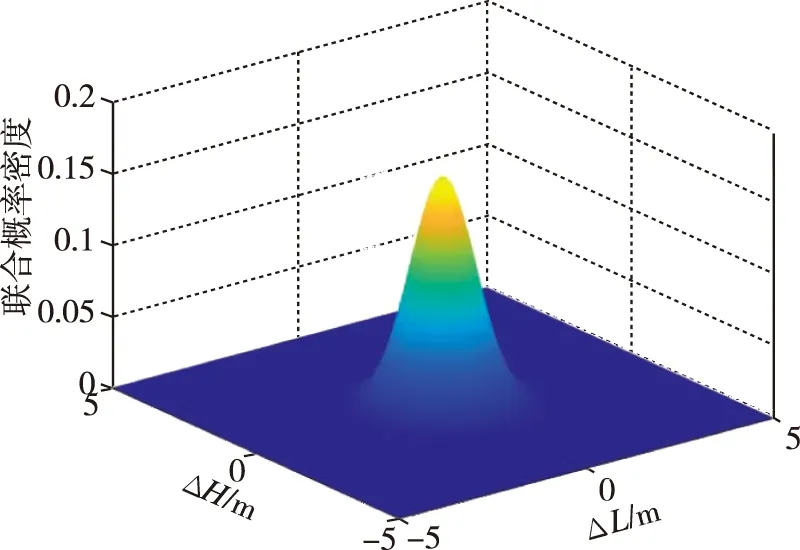
图2 联合概率密度图Fig.2 Joint probability density
2.2 概率偏差
随机变量ΔL,ΔH的概率偏差BΔL,BΔH也称为公算偏差。公算偏差BΔL,BΔH对称于散布中心,落点出现于其中的概率等于0.5区间长度的一半,即
P{|ΔL| (5) P{|ΔH| (6) 根据拉普拉斯函数 (7) 则有 (8) (9) 由拉普拉斯表可知[4] (10) (11) 圆概率偏差(Circular Error Probable,CEP)是以散布中心为圆心,以R为半径画圆,飞行器落在该圆内的概率为50%,此R亦称为半数必中圆半径。 满足下式的R即为CEP P= =0.5 (12) 在点目标假设的条件下,以瞄准点为圆心,假设落点偏差服从正态分布且纵横向独立,即ρ=0,则CEP可表示为[5-8] =0.5 (13) 当落点散布具有圆散布特性,即 (14) 则有[9] (15) 进而有 CEP=1.177 4σ=1.745 6B (16) 式(16)为圆散布情况下圆概率偏差CEP、均方根误差σ和概率偏差B之间的相互转化关系。 在满足一定计算精度的情况下,为快速计算CEP,可建立CEP的拟合公式[10-11]。通过数值计算确定CEP与σΔL,σΔH的拟合关系如下 CEP= (17) 式中 σmin=min(σΔL,σΔH) (18) CEP与σmin/σmax的关系如图3所示。图中红色实线为σmin/σmax∈(0,1)时CEP/σmax与σmin/σmax的关系曲线,蓝色虚线为σmin/σmax∈(0,0.3)时采用线性拟合公式CEP=0.562σmax+0.615σmin所得的CEP/σmax与σmin/σmax的关系曲线。 图3 CEP与σmin/σmax关系曲线图Fig.3 The relationship between CEP and σmin/σmax 从图3可见,在0<σmin/σmax≤0.3时,采用线性拟合公式较采用二次曲线拟合公式会产生较大的误差,且随着σmin/σmax减小,计算误差增大,最大时误差可达17%。因此为准确表征CEP,应采用分段拟合公式,即在0<σmin/σmax≤0.3时采用二次曲线拟合公式,在0.3<σmin/σmax<1时采用线性拟合公式。 CEP与概率偏差的拟合关系如下 CEP= (19) 式中 Bmin=min(BΔL,BΔH) (20) CEP与Bmin/Bmax的关系如图4所示。图中红色实线为Bmin/Bmax∈(0,1)时CEP/Bmax与Bmin/Bmax的关系曲线,蓝色虚线为Bmin/Bmax∈(0,0.3)时采用线性拟合公式CEP=0.833 2Bmax+0.911 8Bmin所得的CEP/Bmax与Bmin/Bmax的关系曲线。 图4 CEP与Bmin/Bmax关系曲线图Fig.4 The relationship between CEP and Bmin/Bmax 从图4可见,在0 本文首先给出了点目标假设下均方根误差、概率偏差和圆概率偏差的定义和计算公式,然后通过理论推导和数值计算给出了二维精度指标相互转换的拟合公式,实现二维精度的快速评估计算。2.3 圆概率偏差
2.4 指标体系相互关系
σmax=max(σΔL,σΔH)
Bmax=max(BΔL,BΔH)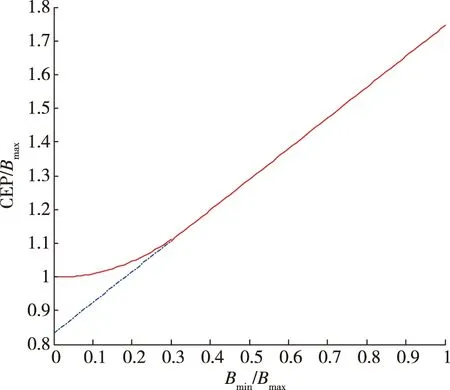
3 结论
