一类潜伏期传染且具有病毒变异的传染病模型

马怡婷，张太雷*，邓金超，刘俊利

（1.长安大学 理学院，陕西 西安 710064；2.西安工程大学 理学院，陕西 西安 710048）

0 引言

传染病动力学模型在理解传染病的传播规律和预测传染病的传播趋势中起着重要作用。早在1927 年，Kermack 和Mckendrick 就建立了SIR 传染病模型［1］，这种“仓室”建模思想一直被广泛使用且在不断地发展［2-7］。近年来，疾病具有潜伏期且潜伏期具有传染性的动力学模型已引起许多学者关注［8-10］，通过对潜伏期与染病期均传染的传染病模型的研究，说明了忽略潜伏期会影响参数估计的准确性，进而对疾病的控制产生很大影响。

医疗数据统计发现，一些传染病在其传播过程中会发生病毒变异，使其难以控制，极易导致传染病暴发。一旦传染病蔓延，将对人类健康与社会发展造成严重威胁，例如禽流感病毒（H7N9），新型冠状病毒（COVID-19），乙肝等疾病。特别是COVID-19，疫情暴发初期，国内累计确诊人数与死亡人数都在不断增加，有多名医务工作者死于COVID-19，疫情给国家造成了人力、物力和财力的巨大损失。随着疫情的不断发展，新冠病毒开始变异，出现了多种具有较强传播力与潜伏性的变异病毒。根据文献［11］，新冠变异病毒德尔塔毒株最早于2020 年10 月在印度被发现，比阿尔法毒株（英国首先报告的B.1.1.7 变异新冠病毒）更易传播，至2021 年6 月24 日已扩散到92 个国家，更易传播的德尔塔毒株为全球抗疫带来新挑战。因此，研究病毒变异的过程有助于了解传染病的传播规律和更好地控制传染病。关于病毒变异的传染病模型已有很多研究工作：Gao 等［12］研究了一类具有病毒变异Logistic 死亡率的SEIR 传染病模型，证明了平衡点的全局稳定性，并分析了模型中参数对疾病传播的影响；李冬梅等［13］建立了具有自发病毒变异的时滞SIR 传染病模型，给出了平衡点的存在性、局部稳定性的充分条件，并通过数值模拟的方法分析了病毒自发变异对疾病传播的影响；杜金姬等［14］研究了一类具有病毒变异且具有Logistic 死亡率的SEIR 传染病模型，证明了随机系统全局正解的存在唯一性，并建立了传染病灭绝的条件。

以上模型虽然考虑到了疾病在传播过程中发生病毒变异，但均未考虑疾病潜伏期具有传染性，且未对模型作具体的疾病应用。因此，本文将建立一类潜伏期和染病期均传染且具有病毒变异的SEI1I2QR 模型。在第2 节，给出模型的基本再生数ℜ0与各类平衡点的存在性，并证明各类平衡点的全局渐近稳定性。第3 节，根据印度COVID-19 的累计病例数对所建模型进行拟合，对疫情的发展趋势进行回溯性研究，并对阈值ℜ0中的部分参数进行敏感性分析，根据分析结果提出合理的建议。第4 节，对全文进行总结。

1 模型建立

从易感者到感染者会有一段潜伏期，这段时期主要表示从易感者到染病者所需要的时间，用仓室E来表示。将某一区域在t时刻的总人数N(t)分为易感者S(t)、潜伏者E(t)、病毒变异前的染病者I1(t)、病毒变异后的染病者I2(t)、隔离者Q(t)和治愈者R(t)，建立了一类潜伏期和染病期均传染且具有病毒变异的SEI1I2QR 模型。对模型作出以下假设：

（1） 易感人群常数输入，输入率为Λ，μ是人们的自然死亡率。

（2） 易感者与潜伏者、病毒变异前染病者和病毒变异后染病者有效接触后都需经过一定的潜伏期，并且潜伏期相同。

（3） 病毒进入易感者体内经过潜伏期后，部分易感者转移为病毒变异前染病者，转移率为ε，此时病毒在这过程中发生变异，部分转化为病毒变异后染病者，变异率为σ。

其他参数是典型的传染病动力学建模参数，其含义明确。β1表示易感者与潜伏者的有效接触率；β2表示易感者与病毒变异前的染病者的有效接触率；β3表示易感者与病毒变异后的染病者的有效接触率；μ1表示潜伏者的隔离率；μ2、γ1、α1分别表示病毒变异前的染病者的隔离率、治愈率、因病死亡率；μ3、γ2、α2分别表示病毒变异后的染病者的隔离率、治愈率、因病死亡率；γ3、α3分别表示隔离者的治愈率、因病死亡率。从生物数学的角度考虑，规定所有参数都非负，所以传染病模型仓室图如图1 所示。

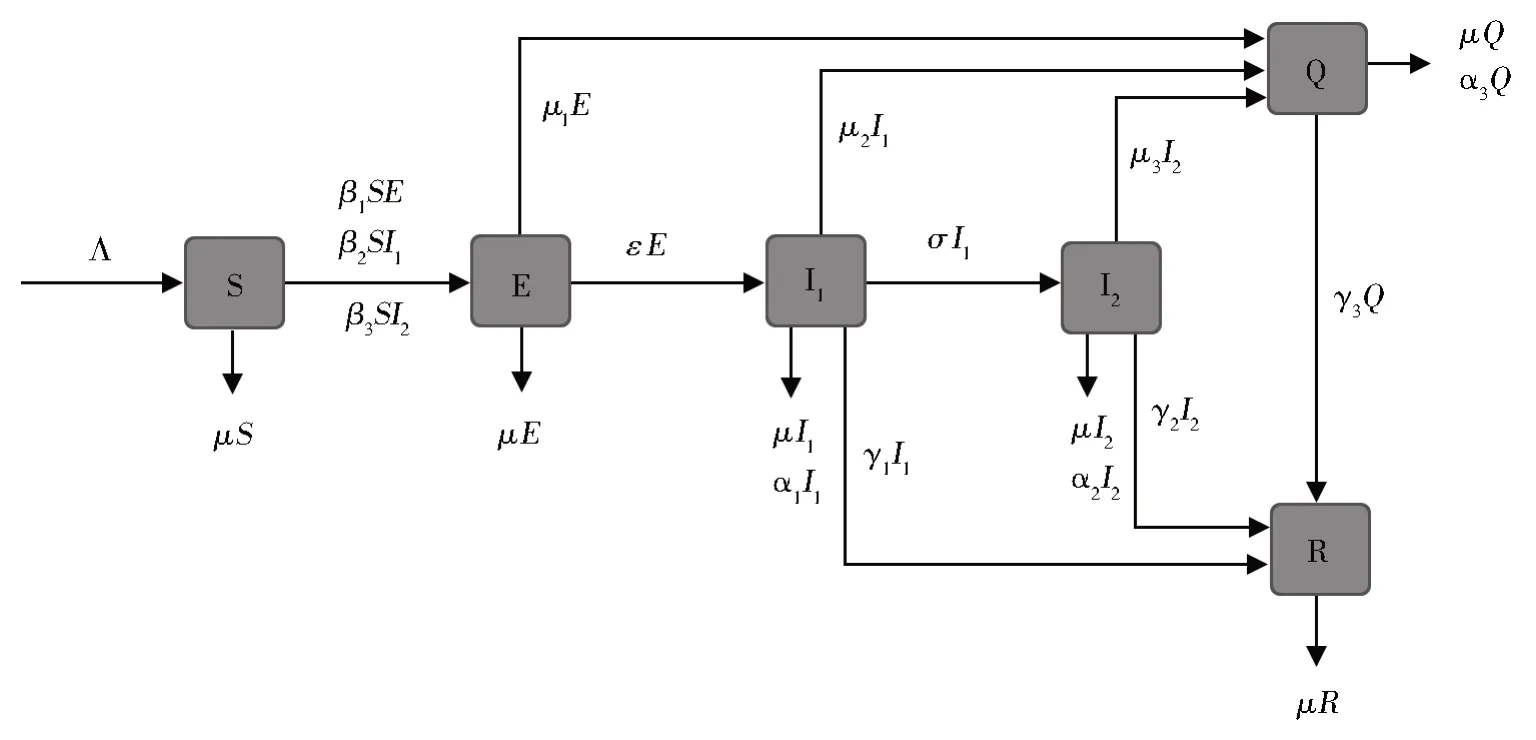
图1 模型的仓室结构图Fig.1 Compartment structure diagram of model

根据假设（1）—（3）与仓室结构图1，相应的传染病模型如下：

2 平衡点的存在性与稳定性

研究模型（1）的动力学性质首先要确定其平衡点，且平衡点的稳定性可以为传染病的控制提供有力的参考价值，因此本节将讨论平衡点的存在性与稳定性。

2.1 平衡点的存在性

为方便起见，记δ1=μ+ε+μ1，δ2=μ+μ2+α1+γ1+σ，δ3=μ+μ3+α2+γ2，δ4=μ+α3+γ3。模型（1）的平衡点满足方程组

易知模型（1）总存在无病平衡点P0(S0，0，0，0，0，0)，其中。根据文献［15］中的再生矩阵法，可定义出模型（1）的基本再生数为，直接计算，当ℜ0＞1 时存在唯一的地方病平衡点P*(S*，E*，I1*，I2*，Q*，R*)，其中

因此，可得如下关于平衡点存在性的定理。

定理1当ℜ0≤1 时，模型（1）仅存在无病平衡点P0(S0，0，0，0，0，0)；当ℜ0＞1 时，模型（1）既存在无病平衡点P0，还存在唯一的地方病平衡点P*(S*，E*，I1*，I2*，Q*，R*)。

2.2 无病平衡点的稳定性

无病平衡点对应于疾病的消亡，无病平衡点稳定说明易感者的人数最终会趋于一个常数，变异前后的染病者人数都将趋于零。本小节将研究无病平衡点的稳定性。

定理2当ℜ0＜1 时，无病平衡点P0局部渐近稳定；ℜ0＞1 时，无病平衡点P0不稳定。

证明模型（1）在无病平衡P0处的Jacobi 矩阵为

显然，J(P0)有六个特征根λi(i=1，2，…，6)，其中λ1=λ2=-μ，λ3=-δ4且λ4，λ5，λ6满足方程λ3+a1λ2+a2λ+a3=0，这里

当ℜ0＜1 时，

依据Routh-Hurwitz 准则，J(P0)的所有特征根均有负实部，所以无病平衡点P0局部渐近稳定；当ℜ0＞1 时，a3＜0，则J(P0)存在正实部特征根，因此无病平衡点P0不稳定。

定理3当ℜ0＜1 时，无病平衡点P0全局渐近稳定；当ℜ0=1 时，无病平衡点P0全局吸引。

证明构造Lyapunov 函数

V1(t)关于模型（1）对t求导有

2.3 地方病平衡点的稳定性

地方病平衡点稳定说明疾病会持续存在，病毒变异前后的染病者最终趋于一个常数，疾病形成一种地方病。本小节将从理论上证明地方病平衡点的稳定性。

定理4当ℜ0＞1 时，地方病平衡点P*局部渐近稳定。

3 模型应用

根据模型（1）的特点，本节将对印度的COVID-19 进行研究。

3.1 数据

本文搜集了印度2020 年12 月1 日至12 月30 日的累计病例数据［16］，如图2 所示。

图2 2020年12月1日至12月30日的印度累计病例数Fig.2 Cumulative number of cases in India from December 1,2020 to December 30,2020

3.2 模型参数估计

印度2020 年总人口13.8 亿人［17］，出生率1.873 8%［17］，因此Λ=25 858 440。人口的平均寿命为68.89 年［17］，可取μ=3.977×10-5，新冠的潜伏期一般为7 天［18］，所以取ε=0.14。假设S(0)=13.8×108，取变异前的染病者初值为11 月30 日的累计病例数，所以I1(0)=9 463 256。

根据印度12 月1 日至12 月30 日的COVID-19 累计病例数，对模型（1）的未知参数进行估计，参数的估计值见表1。模型拟合结果如图3 所示。根据表1 中的参数，可得到变异后的染病者的人数变化趋势，如图4 所示。图4 的结果表明变异后的染病者的人数随时间的变化在不断增长，由于变异病毒具有更强的传染性，印度需对其重视起来，并采取相关应对措施，防止疫情的进一步扩散。

表1 模型（1）的参数值Table 1 The parameter values of model (1)

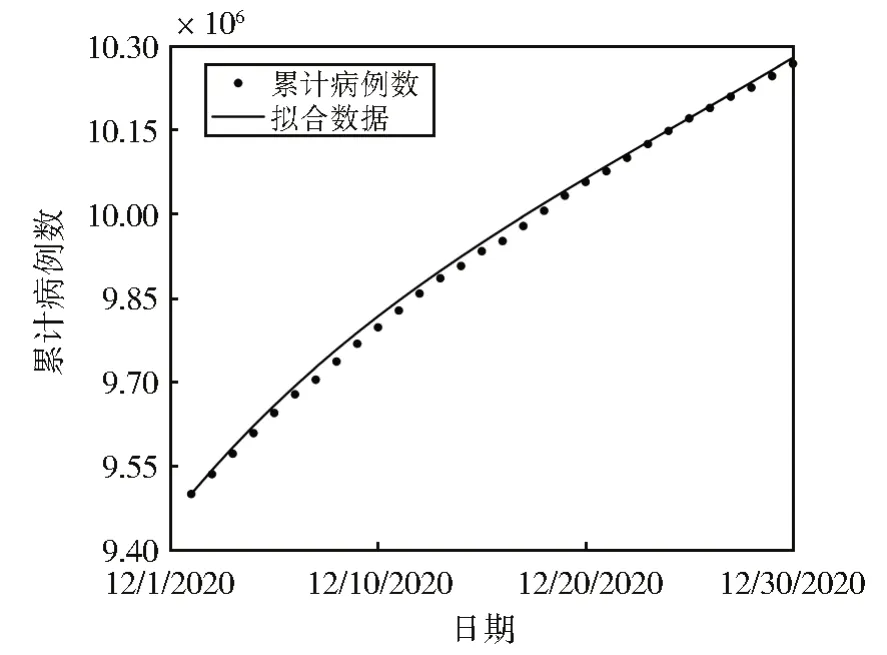
图3 2020年12月1日至2020年12月30日累计病例数与模型（1）拟合Fig.3 The cumulative cases from December 1, 2020 to December 30, 2020 were fitted to model (1)

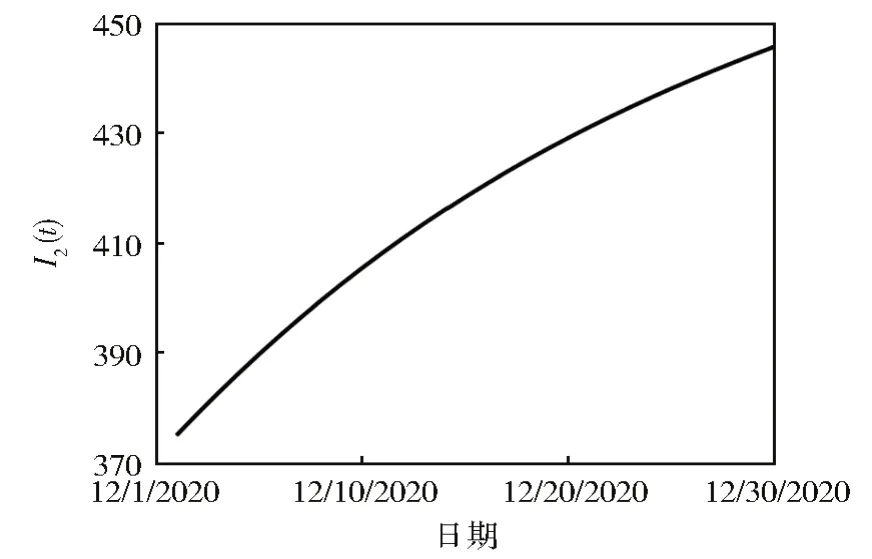
图4 2020年12月1日至2020年12月30日I2(t)变化趋势Fig.4 Change trend of I2(t) from December 1, 2020 to December 30, 2020

3.3 新冠流行趋势

印度后期将接种新冠疫苗，疫苗的接种会影响累计病例人数，且后期新冠康复者会感染毛霉菌病，所以模型不能进行长时间段的预测，因此仅对模型（1）关于印度未来半个月的疫情情况进行预测。对印度2020 年12 月31 日至2021 年1 月14 日累计病例数的预测如图5 所示。从观察到的数据可以看到，印度疫情正在不断加重，还须保持高度警惕，加强防控措施。

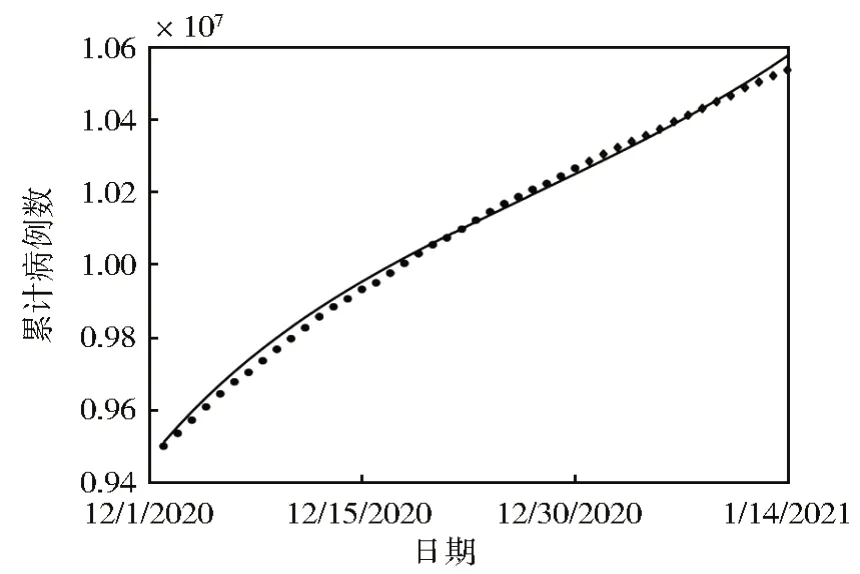
图5 2020年12月1日至2021年1月14日累计病例数与模型（1）拟合的数据对比Fig.5 Cumulative cases from December 1, 2020 to January 14, 2021 were compared with model (1) fitted data

3.4 参数敏感性分析

理论分析表明，基本再生数ℜ0是决定传染病流行的一个重要参数。为了更好的分析各参数与ℜ0的关系，找到控制传染病传播的理论依据，利用PRCCs（偏秩相关系数） 方法对模型（1）的ℜ0进行不确定性分析与敏感性分析，以确定各参数对阈值ℜ0的影响大小。若PRCCs 的值为正，则表示该参数的增加会导致ℜ0的增大；若PRCCs 的值为负，则表示该参数的增加会导致ℜ0的减小。PRCCs 的绝对值在 0～0.2 之间表明输入参数与输出变量之间不存在显著相关性。PRCCs 的绝对值在0.2～0.4 之间表明输入参数与输出变量之间存在中度相关性。PRCCs 的绝对值在0.4～1 之间表明输入参数与输出变量之间具有较高的相关性［19］。本文选取8 个参数β1、β2、β3、μ1、μ2、μ3、γ1、γ2进行敏感性分析，分析结果如图6 所示。从图6 中可以看出，在这些参数中，β1、β2、β3对ℜ0有正影响，μ1、μ2、μ3、γ1、γ2对ℜ0有负影响，与ℜ0有强相关性的参数为：易感者与潜伏者的有效接触率β1、易感者与变异前的染病者的有效接触率β2。该结果表明β1与β2对印度疫情的控制更加有效。

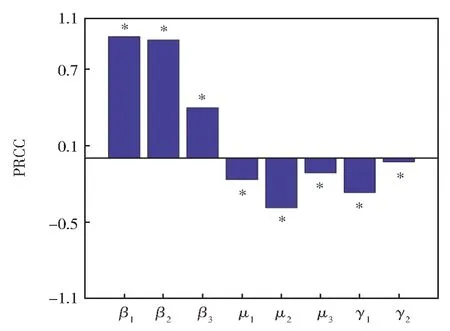
图6 部分相关系数（PRCCs）的结果Fig.6 Results of Partial Rank Correlation Coefficients (PRCCs)

因为β1与β2的PRCC 值相近且讨论方式相似，因此下面仅重点讨论参数β1对变异前染病者I1(t)的累计病例数的影响，结果如图7 所示。从图7 中可以看到，当参数β1减小0.8 倍时，随着时间的推移，变异前染病者的累计病例数将持续减少，且效果逐渐明显。但由于印度疫情较为严重，疫情的控制还需很长时间。

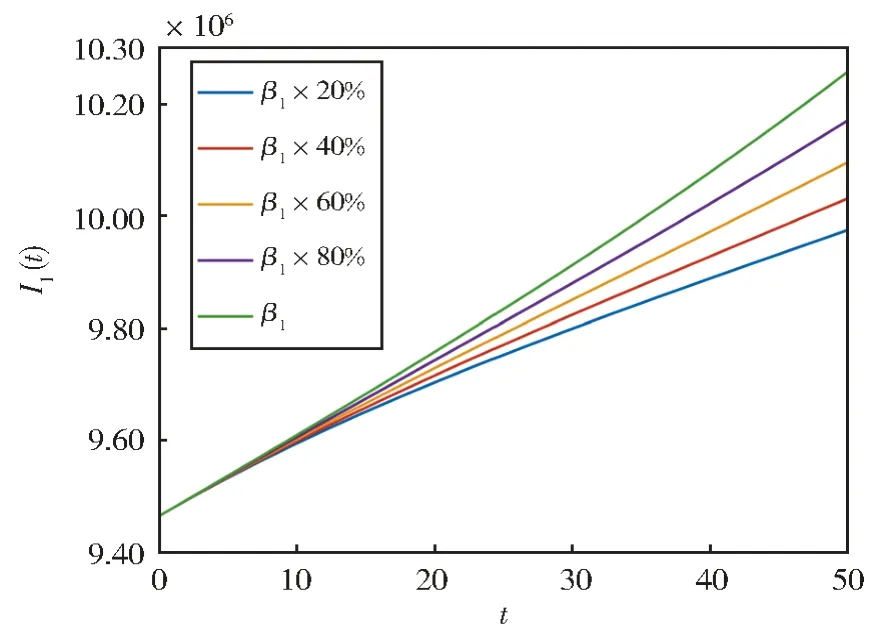
图7 β1变化对I1(t)数量的影响Fig.7 Effect of β1 change on the number of I1(t)

在实际的疫情防控中，将多种有效措施结合起来会产生更好的效果，更加利于疫情的控制。经过分析可以得到几个降低与控制该传染病的有效方法：

（1） 控制易感者与潜伏者的有效接触率β1其降低，控制易感者与变异前的染病者的有效接触率β2使其降低，控制易感者与变异后的染病者的有效接触率β3使其降低，控制潜伏者、变异前的染病者与变异后的染病者的隔离率μ1、μ2、μ3使其增大，即在面对传染病时，国家应采取严格的防控措施，例如；“封城”“居家隔离”等，特别是针对变异前的染病人群，要求居民自觉居家隔离，不出门，不串门，使易感人群避免接触染病者，以切断疫情的传播途径。

（2） 控制变异前的染病者与变异后的染病者的治愈率γ1、γ2使其增大，即缩短染病者的治愈周期，因此在卫生防疫及提高医疗水平方面要有所提升。根据上面的分析，参数γ1对疫情控制更加有效，因此在医疗方面，需更加注重对变异前的染病者的治疗。

（3） 控制人口的常数输入使其减小，即降低不同区域间人口的流动性。

4 结论

本文研究了一类潜伏期具有传染性的SEI1I2QR 传染病模型，考虑了传染病在传播过程中部分染病者的病毒发生变异，成为一类新的染病者。通过研究模型平衡点的存在性与稳定性，得到如下结论：当ℜ0≤1 时，传染病灭绝；当ℜ0＞1 时，传染病蔓延。同时结合模型特点，将印度的COVID-19 作为传染病例子进行数值模拟，结果表明2020 年12 月1 日至12 月30 日的拟合结果与实际COVID-19 的累计病例数据基本符合，并预测了2020 年12 月31 日至2021 年1 月14 日的疫情情况，结果表明在短时间内印度疫情会越来越严重，且变异的染病者会越来越多。最后对模型的基本再生数ℜ0中的部分参数进行了敏感性分析，分析结果表明采取降低易感者与染病者的有效接触率、加强对人口的隔离、提高染病者的治愈率、减少人口流动性等措施可以降低疫情的传播。

年龄对于传染病的流行规律是一个很重要的因素，因为不同年龄段的人有着不同的死亡率，年龄也影响着传染率与恢复率等疾病传播因素，因此考虑具有年龄结构的模型是非常有必要的。其次，时滞在传染病的传播过程中也扮演着一个重要的角色，可以用时滞模拟传染病的潜伏期、患者对疾病的感染期和恢复者对疾病的免疫期，因此考虑具有时滞的模型可以减小预测与实际之间的误差。我们将在将来的研究工作中考虑这些问题。