基于互信息的异步电动机轴承故障特征选择方法研究*
2023-06-05周智勇杨理华
刘 文 周智勇 蔡 巍 杨理华
(海军潜艇学院 青岛 266000)
1 引言
异步电动机故障类型主要包括轴承故障、定子匝间短路、转子断条和气隙偏心等。其中,轴承故障占比最高,约占异步电动机故障统计的40%~50%。因此对异步电动机的轴承实施故障诊断具有重要的现实意义。
传统的轴承故障诊断方法主要是依靠故障特征频率进行判断,但易受到其他高频信号干扰,对使用环境有一定限制。近年来,数据驱动技术的发展,为电机轴承故障诊断提供了新思路,即通过电动机的运行数据分析轴承状态,而运行数据的特征选择正是该类诊断算法的核心内容。适当的特征选择算法能够对高维故障特征集进行有效降维,筛选得到与电机状态高度相关的特征集,从而大幅降低故障诊断算法运行时间。
本文通过引入信息论中互信息的基本概念,以运行数据统计量与设备状态的互信息为评价准则,提出基于异步电动机振动信号的轴承故障特征选择算法。试验表明:该算法能够在降维条件下,有效筛选数据特征集,提高诊断效率。
2 互信息的基本概念
互信息以信息论为背景,能够衡量两个变量的相互依赖程度,表示两个变量间共同拥有信息的含量[1]。下面对基于互信息的特征选择算法涉及基本概念进行介绍。
概念1信息熵。信息熵是通过统计学的方法,反映随机变量内部不确定程度的量,体现随机变量所蕴含信息量的大小。假设X={x1,x2,…,xn} 为一个随机变量,则其信息熵H(X)表达式为
其中,p(xi)为xi发生概率。
p(xi)在极限情况下,当随机变量X中的变量均为x 时,p(xi)=1。此时信息熵H(X)=0,表明样本集包含的信息量为零。
概念2条件熵。条件熵H(X|Y)表示在给定Y变量的条件下X变量的不确定程度,定义如下:
概念3互信息。对于两个随机变量X、Y,它们的互信息定义如下:
互信息还可以表示为
I(X;Y)=H(Y)-H(Y|X)
当X 与Y 相互独立时,则H(Y|X)与H(Y)相等,此时I(X;Y)=0。
概念4相关性。假设Xm为待选特征集合,C为类标签集合。相关性用于表征特征集中的特征与标签集中的标签的关联程度,通过互信息I(Xm;C)直观体现。I(Xm;C)越大,则特征向量与类标签关联度越高。
概念5冗余性。假设S 为已选择的特征集合,则冗余性表示待选的特征向量与S 的相关性,同样以互信息为衡量标准。
3 基于互信息的轴承故障特征选择
3.1 特征选择
数据驱动算法,是由电动机运行原始数据提取的统计特征,反映设备运行状态。对应不同故障类别时,可将其特征划分为强相关性特征、无关特征和冗余特征[2]。依据数据特征进行故障诊断时,高维数据特征集可以提高故障诊断的识别能力,但同时不可避免引入的计算冗余和非显著信息,会降低后验故障检测和识别性能。因此,在数据驱动算法中进行特征选择,其目的就是要按照某种评价原则,筛选出最具有代表性的特征量,排除无关特征和冗余特征,降低特征集维度,避免出现故障检测效率低下和结果过拟合等问题。数据特征选择的基本流程参见图1。

图1 数据特征选择的基本流程图
3.2 基于互信息的特征选择
特征选择即是在原有特征集中,筛选出强相关性的特征,形成一个新的集合,降低特征集维度,但又不过分减少信息量。数据特征选择的选择过程是通过评价准则来实现的,目前主要有主元分析法(Principle Component Analysis,PCA)、线性判别分析法(Linear Discriminate Analysis,LDA)等,但PCA不适用于处理非线性关系,LDA则会产生新的特征量,可解释性差。而基于互信息的特征选择算法以互信息为评价准则,能够衡量变量间的相互依赖程度,提取有效特征,对非线性问题的处理也同样适用。
基于互信息的特征选择算法一般是通过遍历特征集合,选择与类标签相关性最大的特征,形成新的集合,该方法称为最大互信息算法(Mutual Information Maximum,MIM)。
假设F为原始特征集合,S为已选特征集合,Xm为待选特征集合,C为标签集,则MIM 的评价准则为
JMIM(F,C)=I(fi;c)
通过遍历F,寻找与C相关度最高的特征向量,放入S中,并从F中删除;重复上述过程,直到找到m个最优特征向量。该方法计算量小,能够很好地找到与类标签高度相关的特征量,但没有考虑到已选特征量xs与待选特征量xm之间的相关性。
基于MIM算法的不足,修改其评价准则为
即得到了最大相关最小冗余算法[3](Feature selection based on maximum-relevance and minimum-redundancy,mRMR)。
与MIM 算法不同,该方法引入了冗余度的概念,其评价准则分为两部分,前半部分I(xm;c)为待选择特征与类标签的相关性,后半部分为待选择特征与已选特征间的冗余度。通过遍历F,找到与类标签高度相关,同时与已选择特征低冗余的特征向量,也即是使评价准则最大化的特征向量,放入S中,并从F中删除,重复上述过程,直到找到m个最优特征向量。mRMR算法流程如图2所示。
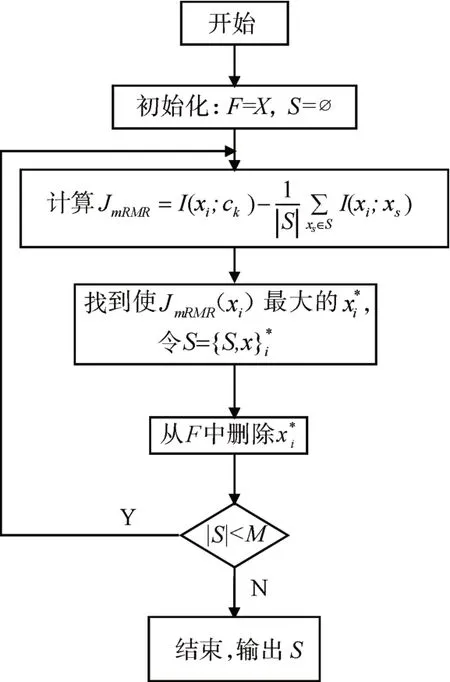
图2 mRMR算法流程框图
由图2可见,mRMR 算法在计算冗余度时采用加权的方法,能够实现评价准则的动态调整,使运算结果更加合理。
3.3 异步电动机轴承故障特征选择
当异步电动机发生轴承故障时,其振动特性将发生改变,因此通过分析电机振动信号时域统计特征量可对轴承故障进行诊断。常用的时域统计特征包括方差(Variance,σ2)、均方根(Root mean square,RMS)、偏度(Skewness,Sk)、峰度(Kurtosis,Ku)、最大值(Maximum,Max)等,表1中列举了本文中使用的13 种时域统计量及其计算公式,它们在故障诊断领域中得到广泛使用[4~5]。

表1 时域统计特征及其计算公式
不同的统计特征量可以从不同角度反映异步电动机振动信号的变化趋势,如方差和标准差可以用于描述振动信号数值的集中和分散程度;均方根可以反映振动信号的有效值;偏度能够判定振动数据分布的不对称程度及其方向;峰度能够判定数据分布是更陡峭还是平缓。传统的诊断方法可以根据某种统计量的变化程度判别轴承故障,但这种方法比较粗糙,且易受外界环境因素的影响。通过基于互信息的特征选择算法,找到与类标签相关度最高的那部分统计量,可以很好地解决该问题,且可避免计算冗余和结果过拟合。
对采集得到的振动信号按照表1中的公式提取13种时域统计特征量,形成原始特征集。从表1中可以看出各统计量的量纲各不相同,在图3中以Sk1和Ku1为例,描绘了二者的幅值对比图,可以明显看出其幅值大小上存在明显差异。基于上述问题,在进行互信息值计算前,首先需要对各统计量进行归一化处理,以便得出更为准确的结论。区分健康和轴承故障两种类标签,分别计算各特征向量与类标签的互信息值。通过mRMR算法,计算得到特征量与类标签的相关度,并依照互信息大小排序。排名越靠前,则代表相关度越高且具有较低的冗余度。采用排名靠前的特征形成特征集,从而可在低数据维度条件下,对轴承故障进行诊断判别。
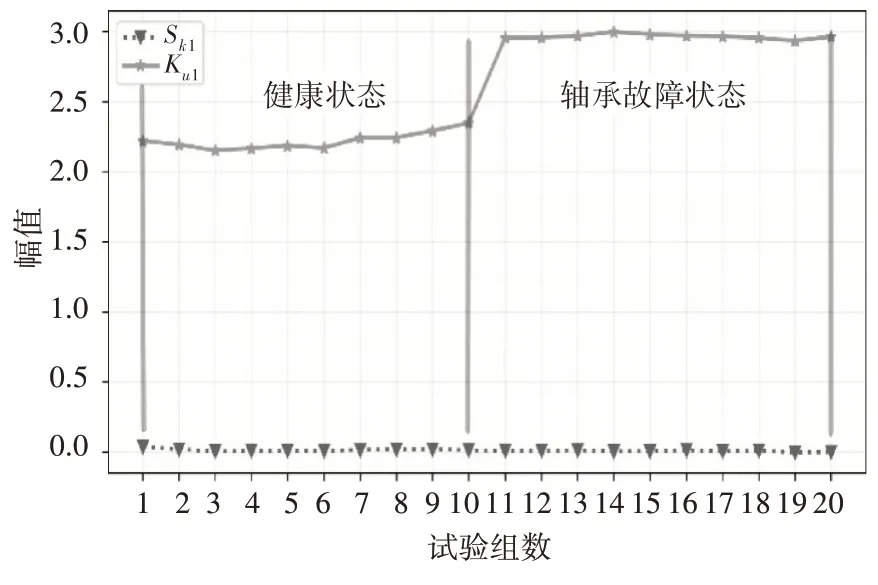
图3 Sk1、Ku1 幅值对比图
4 试验验证
4.1 试验平台
将本文算法在试验平台予以验证。试验平台主要包括异步电动机、直流发电机、电阻负载箱、信号采集仪和上位机等。其中,异步电动机功率为7.5kW,型号Y132M-4;直流发电机与异步电动机同轴连接,作为拖动负载使用;直流发电机输出连接电阻负载箱,从而实现功率调整。试验装置如图4所示。

图4 试验装置平台
为获取电机运行过程中的振动信号,试验安装有2 个LC0104 型振动加速度传感器,量程0~50g。其中,1 号传感器布置于故障轴承端的近端盖基脚位置,2 号传感器布置于故障轴承端的端盖径向侧,如图5所示。信号采集和存储由一台16通道信号采集仪完成,型号为INV3062A2,采样频率10kHz。

图5 传感器布置图
4.2 轴承故障试验
在异步电动机内模拟轴承外圈故障,轴承型号为6308A,在轴承外圈处开贯穿型凹槽,开槽宽度为5.0mm,深度为1.5mm,如图6所示。

图6 故障轴承图
分别在健康和轴承故障状态下,采集2 处测点的振动信号,采集时间宽度50s,如图7所示(图中仅显示1024个采样点)。从图中可以明显看出,当发生轴承故障时,振动信号幅值明显增大,且端盖径向侧振动信号明显强于近端盖基脚位置振动信号。
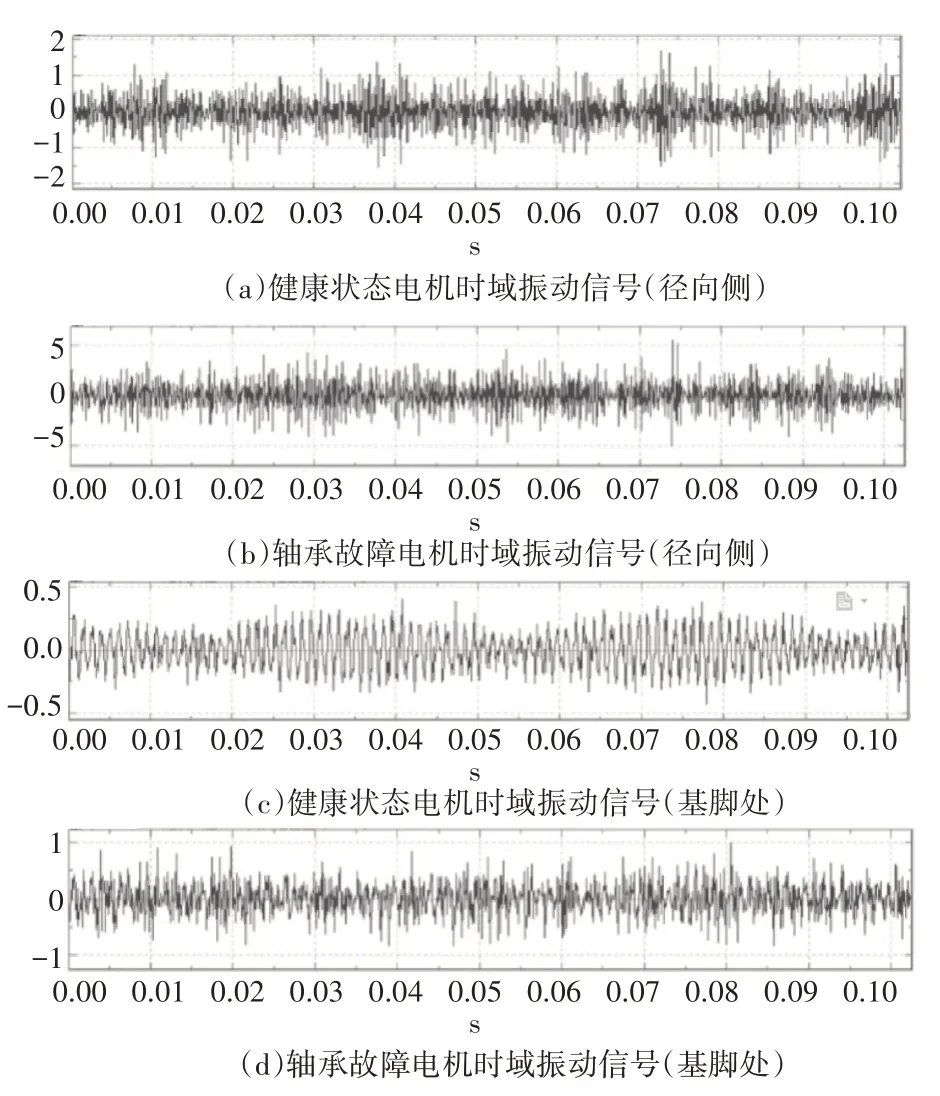
图7 振动信号图
4.3 结果分析
为进行对比分析,首先采用MIM 算法计算各特征量与类集合C 的互信息值,其排序情况如下式(下标代表对应的传感器代号):
SRMsf2>RMS2>SD2>SRM2>σ22>Ku1>SD1>RMS1>SRMsf1>RMSsf1>Max2>σ21>SRM1>Max1>IF1>LF2>CF1>LF1>Ku2>Xˉ2>RMSsf2>Sk1>CF2>IF2>Sk2>
经过排序后的特征向量,排名越靠前的特征量与类的相关度越高。选取SRMsf2、IF1、进行对比分析,如图8中所示,可以看出三者的数据分布存在明显差异,SRMsf2、IF1具有更好的数据集中度,且在健康和轴承故障状态下有明显的区分度。
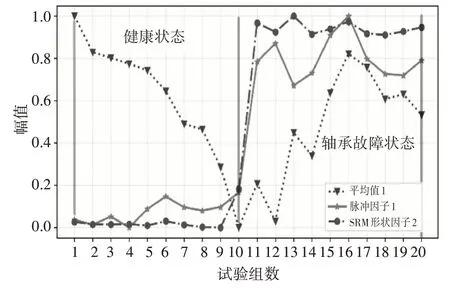
图8 SRMsf2、IF1 与 对比图
再使用mRMR 算法对特征向量与类集合C 的互信息值进行计算,得出排序情况如下:
SRMsf2>SRM2>RMSsf1>Max2>CF1>σ22>RMS2>SD2>SD1>Ku1>LF1>RMS1>IF1>LF2>SRMsf1>Max1>σ21>SRM1>Ku2>Sk1>RMSsf2>CF2>>IF2>Sk2>
通过对比mRMR 算法和MIM 算法排序结果,SRMsf2始终排在所有特征向量的第一位,这说明不论MIM 或mRMR 算法,在初次遍历原始特征集后得到的结果一致,SRMsf2与类标签的相关度最高。
结合MIM 和mRMR 算法的排序结果也可以看出,在mRMR 算法中,RMS2的排名发生了明显的变化。这是因为,SRMsf2与RMS2的图形走势几乎完全一致(参见图9),其特征量分布情况高度集中,反映其与类标签拥有高相关度,但同时也说明两特征间的冗余性很高,即MIM 算法无法避免数据冗余。而mRMR 算法可以有效避免这一问题,SRM2因其与SRMsf2冗余度低,且同样具有较高的类标签相关度,排名得到提升。
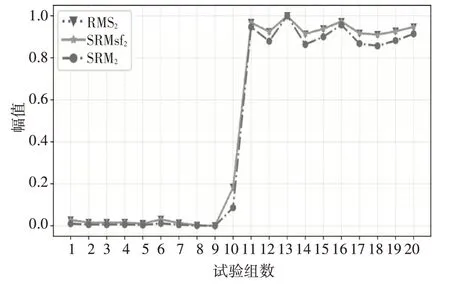
图9 SRMsf2、RMS2 与SRM2 对比图
此外,通过观察两类互相关算法结果,端盖径向侧的特征向量排名比较靠前,其与类标签相关度更高,在传感器布设数量受限的条件下,可优先考虑在端盖径向侧位置布设振动传感器。
5 结语
针对异步电动机轴承故障诊断中对数据降维的需要,从互信息基本概念出发,就其在特征选择算法中的实际应用进行了研究。以异步电动机振动时域信号的统计量为样本,并进行归一化处理。经MIM、mRMR 算法排序后的试验结果表明:MIM算法可以有效区分数据样本与类标签的关联程度,但无法避免数据冗余;而进行mRMR 算法排序时,若样本拥有相似数据分布趋势,则其冗余度较高,算法会将其推后。因此,mRMR算法中排名靠前的特征量,其与类标签的相关度高,且特征间的冗余度低。因此,基于互信息的轴承故障特征选择算法,能够在异步电动机轴承故障诊断中实施有效降维,提高计算效率。
