基于定向天线的通信系统波束指向偏差模型*
2023-06-05高龙超
高龙超
(中国西南电子技术研究所 成都 610036)
1 引言
无线电通信中的数据链是机载平台实现信息共享、协同作战的重要支撑,其可传输战术数据、图像以及自由文本等,数据链在战场上扮演着各作战单元粘合剂的角色[1]。数据链要实现机载平台与其他作战单元的互联互通,不可避免要进行电磁辐射。而随着无源探测技术的发展,现代战场机载平台的生存环境日益恶劣,反辐射定位跟踪技术对机载平台造成了很大威胁,因此射频传感器低截获的要求被提了出来。数据链实现低截获的措施包括频域上跳频扩频,时域上猝发通信,能量域上功率管理。而使用定向天线的数据链可在空域上降低截获概率。使用定向天线的数据链定向发射、定向接收,因此定向天线的优势除了能够降低截获概率外,还能增强抗干扰能力[2]。另外,定向天线增益高,能够实现较高的传输速率以及较远的通信距离[3~5],而且基于多波束技术可实现定向通信的空分复用,提高网络容量[6]。
实现定向通信的一个前提是两个通信节点天线波束彼此指向对方[7]。对于机载平台尤其是高机动平台,要实现通信双方波束互指要求天线波束能够快速切换。因此高机动平台一般使用相控阵天线实现定向通信,与机械扫描天线相比,相控阵天线除了波束控制灵活、波束响应速度快外,相控阵天线无需伺服系统,天线能够与飞机机体共形,降低了飞机RCS。定向通信系统的波束宽度越窄,其低截获性能越好,但增加了波束对准的难度。波束对准与波束指向偏差和天线波束宽度有关,若能将波束指向偏差控制在天线主瓣中心较小范围内波动,则波束对准情况较好,能够保证通信链路有较高的增益,通信链路会更加稳定。文献[8]给出了使用STK/Matlab 分析定向通信系统波束偏差的方法,并指出波束偏差与外推算法有关。文献[9]给出了天线初始对准与维持波束跟踪的建议,提出使用全域扫描实现天线初始对准,根据定位信息维持波束跟踪。
根据文献[9]的方法,维持波束跟踪需要进行一系列坐标转换,定位信息一般以大地坐标系的形式给出,而最终需要计算出天线坐标系下的波束指向。在坐标转换过程中,定位误差以及坐标系转换误差会导致波束指向出现偏差[10],当天线波束宽度一定时,波束指向偏差直接影响波束能否对准,进而影响定向通信的稳定性。因此,有必要对定向通信的波束指向偏差进行估计。
本文首先建立定向通信系统波束指向偏差估计模型,以波束指向偏差为目标函数,以影响波束指向偏差的误差因子作为约束变量,使用最优化方法对模型进行求解,得到最大波束偏差估计值,根据波束偏差估计值就工程中定向通信系统的关键参数设计给出建议。
2 波束指向计算
根据文献[9]的方法,定向通信系统计算波束指向时,根据双方的位置信息进行计算,双方的位置信息必须在同一坐标系下。因此,一般使用经纬高坐标系下的位置信息进行波束指向计算。由于最终要将波束指向信息下发给天线,因此还需要进行一系列坐标系转换,最终得到天线坐标系下的波束指向。假设点p在经纬高坐标系下的坐标值为(φ,ϕ,h),其中φ为经度,ϕ为纬度,h为高度,点p在大地直角坐标系下的坐标值为(x,y,z),经纬高坐标转换为大地直角坐标系的公式如式(1)所示。
式(1)中,N是基准椭球体的卯酉圆曲率半径,e是椭球偏心率,它们与基准椭球体的长半径a和短半径b的关系如式(2)所示。
式(2)中,f为基准椭球体的极扁率,e为偏心率。a=6378137m,f=1 298.257,为WGS-84给出的基本大地参数值[11]。假设节点p1、p2在经纬高坐标系下的坐标值为(φ1,ϕ1,h1)、(φ2,ϕ2,h2),根据式(1)可计算出p1、p2在大地直角坐标系下的坐标值(x1,y1,z1)、(x2,y2,z2)。根据文献[11]可计算出以p1为坐标原点的站心坐标系下p2的坐标,则站心坐标系下p2相对于p1的方位角AZ、俯仰角EZ如下式所示。
p2相对于p1的单位方向矢量如下述所示:
上式中,[·]T表示转置,计算以p1为原点的天线坐标系下p2的坐标需要依次经过站心坐标系转换到机体坐标系,机体坐标系转换到天线坐标系。坐标系转需要依次经过航向角变换、俯仰角变换以及横滚角变换。
航向变换矩阵如式(6)所示,其中α为航向旋转角。
俯仰变换矩阵如式(7)所示,其中β为俯仰旋转角。
横滚变换矩阵如式(8)所示,其中γ为横滚旋转角。
依次经过航向变换、俯仰变换以及横滚变换的坐标系变换矩阵为T(α,β,γ)=TαTβTγ,如式(9)所示。
若节点p1所在平台的航向角、俯仰角、横滚角分别为α1、β1、γ1,天线的安装航向角、俯仰角、横滚角分别为α2、β2、γ2,则在以p1为原点的天线坐标系下p2的归一化坐标矢量如式(10)所示。
上式中,[·]T表示转置,OP2D如式(5)所示,为归一化矢量,T(αi,βi,γi)(i=1,2)如式(9)所示。由于T(α,β,γ)=TαTβTγ,且Tα、Tβ、Tγ均为单位变换矩阵,则T(α,β,γ)为单位变换矩阵,进一步T(α2,β2,γ2)T(α1,β1,γ1) 亦为单位变换矩阵,且OP2D为归一化矢量,则OP2T亦为归一化矢量。
3 波束指向偏差模型
坐标系转换过程中,引入波束指向计算误差的因素包括:式(3)和式(4)中位置误差导致的站心坐标系下的方位角误差、俯仰角误差,式(10)中平台的姿态角误差包括航向角误差、俯仰角误差、横滚角误差,天线的安装姿态角误差包括航向角误差、俯仰角误差、横滚角误差。
设位置误差导致的站心坐标系下的方位角误差、俯仰角误差分别为dAZ、dEZ,则实际的方位角、俯仰角分别为平台的航向角误差、俯仰角误差、横滚角误差分别为dα1、dβ1、dγ1,则实际的平台航向角、俯仰角、横滚角分别为α1'=α1+dα1,β1'=β1+dβ1,γ1'=γ1+dγ1。天线的航向角误差、俯仰角误差、横滚角误差分别为dα2、dβ2、dγ2,则实际的天线航向角、俯仰角、横滚角分别为根据位置测量数据计算的方位角、俯仰角和平台姿态角、天线姿态角计算得到的波束指向矢量如式(10)所示。将实际的方位角、俯仰角代入式(5),将平台实际姿态角、天线实际姿态角带入式(6)~式(10),可计算得到天线坐标系下实际的波束指向矢量为则由测量值得到的波束指向矢量与由实际值得到的波束矢量二者的夹角如下所示。
式(11)中含根据位置信息计算得到的方位角和俯仰角、平台的姿态角、天线的姿态角以及上述参数的测量误差。根据位置信息计算得到的方位角AZ∈(-180,180],俯仰角EZ∈(-90,90],平台的姿态角中航向角α1∈(-180,180],俯仰角β1∈(-90,90],横滚角γ1∈(-90,90],天线的姿态角中航向角α2∈(-180,180],俯仰角β2∈(-90,90],横滚角γ2∈(-90,90]。位置信息由卫星导航设备给出,平台的姿态角由惯性导航设备测量,天线的姿态角由激光雷达测量。因此根据位置信息计算得到的方位角和俯仰角误差由卫星导航设备决定,dAZ∈[-εAZ,εAZ],dEZ∈[-εEZ,εEZ];平台的姿态角误差由惯性导航设备的精度决定,dα1∈[-εα1,εα1],dβ1∈[-εβ1,εβ1],dγ1∈[-εγ1,εγ1];天线的姿态角误差由激光雷达的精度决定dα2∈[-εα2,εα2],dβ2∈[-εβ2,εβ2],dγ2∈[-εγ2,εγ2]。则定向通信系统的波束指向偏差问题可转化为如下所示的约束条件下的最值问题。
式(12)中,(xT,yT,zT)T为根据位置信息等参数测量值计算得到的归一化波束指向矢量,为根据位置信息等参数实际值计算得到的归一化波束指向矢量。(xT,yT,zT)T由式(5)~式(10)计算得到,与(xT,yT,zT)T的计算过程相同。
4 模型求解
式(12)所示的最值问题涉及多个变量,且各个变量均为连续变量。目标函数涉及式(10)所示的矩阵相乘以及式(12)中的反余弦运算,无法通过常规的最值方法求解。遗传算法是模拟生物进化过程的一种智能算法,由Holland提出,其广泛应用于函数优化问题和组合优化问题的求解,尤其适用于求解非线性问题,而式(12)为典型的非线性最值问题求解。遗传算法包括三个遗传算子,分别是选择、交叉以及变异,算法的主要参数包括种群规模、变异概率、交叉概率以及进化代数等。关于遗传算法的具体操作步骤以及参数设置见文献[12~13]。本文选择算子采用轮盘赌方法;交叉算子采用二进制单点交叉方法;变异算子采用二进制制随机变异法。选择算子基于概率统计的思想,个体的适应度越高,被选择的概率越大,体现了遗传算法“适者生存”的思想,但又能够保证适应度低的个体被选择,只是概率低而已,从而保证了下一代种群的个体多样性。交叉算子用于实现种群个体的更新,将种群中的一对个体的某一段基因片段进行交互形成新的个体。变异算子对个体的基因值进行变动,比如采用二进制编码的个体,将某一位的0 变为1 或者1 变为0 即实现对个体的变异操作。关于参数取值,种群大小取100,进化代数取50,交叉概率取0.8,变异概率取0.09。交叉概率取值较大,是因为其能够实现全域搜索,作为主算子;变异概率取值较小,是因为其能够实现局部搜索,作为副算子;交叉概率取值较大,变异概率取值较小,与遗传学的基本概念一致。
个体采用二进制编码,二进制的位数与变量的精度及取值范围有关,可根据各变量的精度和取值范围计算出各个变量的二进制位数。式(12)中的约束变量dAZ、dEZ取决于卫星导航设备(测量本平台的位置)的精度,dα1、dβ1、dγ1取决于惯性导航设备(测量本平台的姿态)的精度,dα2、dβ2、dγ2取决于激光雷达(测量天线姿态角)的精度,这些误差是随机误差,无法消除,且无法预测补偿。上述参量的精度取10-4,结合变量取值范围可计算出各个变量的二进制位数。应用遗传算法求解最优化问题一般为单变量最值问题,而本文为多变量最值问题,在使用遗传算法的求解过程中需要对多个变量进行遗传算子操作。
5 算例分析
本节根据式(12)中各约束变量的取值范围应用遗传算法进行模型求解。式(12)中AZ、EZ、α1、β1、γ1、α2、β2、γ2八个约束变量的取值范围已经给出,dAZ、dEZ、dα1、dβ1、dγ1、dα2、dβ2、dγ2八个约束变量的具体取值范围没给出,这八个约束变量为AZ等八个约束变量的测量误差,取决于测量仪器的精度。为了对模型进行求解,不妨假设某机载平台惯性导航设备测量的平台航向角误差dα1范围为[-0.2,0.2]、平台俯仰角误差dβ1范围为[-0.2,0.2]、平台横滚角误差dγ1范围为[-0.2,0.2];根据卫星导航设备给出的位置数据计算得到的站心坐标系下通信对象方位角误差dAZ范围为[-2,2]、俯仰角误差dEZ范围为[-1,1];激光雷达测量的天线航向角误差dα2范围为[-0.1,0.1]、天线俯仰角误差dβ2范围为[-0.1,0.1]、天线横滚角误差dγ2范围为[-0.1,0.1]。将上述参数约束带入到式(12)中,采用遗传算法得到最大波束指向偏差为2.4°。表1进一步给出不同变量误差情况下的最大波束指向偏差计算结果。
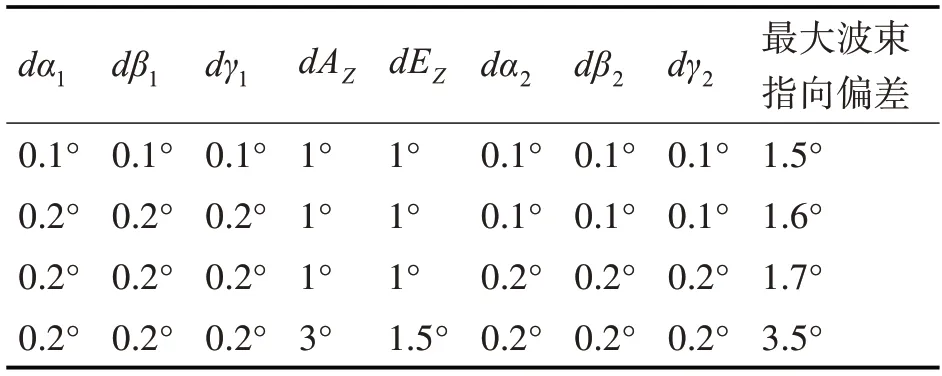
表1 不同变量误差情况下的最大波束指向偏差计算结果
由上表可知,各变量误差越大,波束指向偏差越大。上述八个变量中,dα1、dβ1、dγ1、dα2、dβ2、dγ2直接取决于测量设备的精度;dAZ、dEZ除了与测量设备的精度有关外,还与通信双方的距离有关,在测量设备精度一定的条件下,通信双方距离越近,dAZ、dEZ越大。
式(12)中给出的AZ、EZ、α1、β1、γ1、α2、β2、γ2八个约束变量的取值范围是普适性的,工程实际中可根据通信设备的具体应用将约束变量的取值范围进一步缩小。如天线安装姿态角的取值,天线安装在载机上之后,天线安装姿态角就是固定的,不会发生变化,因此对于具体的定向通信系统,可将α2、β2、γ2取为固定值。对于方位角AZ和俯仰角EZ,由于通信一般需要实现全空域覆盖,因此AZ∈(-180,180],EZ∈(-90,90]。对于载机姿态角,由于α1为航向角,因此α1∈(-180,180],而对于俯仰角β1和横滚角γ1,可根据平台的机动性进行取值范围的确定,如对于战斗机平台,其机动性较强,β1和γ1的取值范围较大,对于运输机以及侦察机等平台,其机动性较小,β1和γ1的取值范围相应较小。
在定向通信系统设计过程中,波束指向偏差是个重要的参考值。波束指向偏差决定了天线波束宽度的设计,一般而言,通信系统能容忍的波束对准损耗较小,因此,若波束指向偏差较大,则相应地要求天线波束宽度较大。若天线波束宽度的设计值无法与波束指向偏差匹配,则要求天线具备更大的功率孔径积,从而弥补波束偏差较大导致的较高的链路损耗。
6 结语
给出了基于定向天线的通信系统波束指向计算过程以及波束指向偏差数学模型,基于该数学模型的特点,提出使用遗传算法进行求解。对模型中约束变量的取值范围进行了分析,使用遗传算法计算了不同情况下的波束指向偏差。本文所建立的数学模型有助于指导工程实际中定向通信的相关设计。
