基于规定性能方法的海上浮式风机独立变桨控制

2023-06-03孙寒冰刘伟杰荆丰梅

哈尔滨工程大学学报 2023年5期

孙寒冰,刘伟杰,荆丰梅

(1.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨 150001;2.北京石油化工学院机械工程学院,北京 102617)

在过去的几十年里,风能已经被证明是最有前途的可再生能源之一。与陆上风机相比,海上浮式风机由于海上风力资源的丰富和高质量,是一种比较有应用前景的可再生能源解决方案。然而,海上复杂的环境给海上浮式风机带来了新的问题,包括额外的波浪载荷、不稳定的平台运动等问题。海上风力发电机系统的结构设计要求能够承受由作用在主要部件上的疲劳载荷引起的恶劣工况,而额外的波浪载荷和平台的反复运动,会加剧这种工况[1]。此外,平台运动增加了输出功率波动。因此,降低这些风机的载荷和平台运动成为控制设计中极其重要但具有挑战性的部分。提供一个控制策略解决这些问题对海上浮式风机的运行是十分重要的。

在额定风速之上时,海上浮式风机的主要控制目标是在保持额定功率的同时减小平台的俯仰运动。在减小平台的运动方面,主要的控制方法基本是基于统一桨距控制,Larsen[2]和Jonkman[3]提出了利用基于增益调度PID反馈控制的统一桨距控制,以减小桅杆浮标平台的俯仰运动。在这些方法中,都是通过减小增益参数使转速控制回路的固有频率低于平台俯仰运动的固有频率。这些控制方法大大减少了平台的俯仰运动。然而由于叶片桨距角变化缓慢,使得功率输出波动变得更加显著。Lackner[4]提出了一种变速操作,该操作中转速增益调度反馈控制的设定值随着平台俯仰速度的变化而变化。这种变速操作成功地减少了平台的俯仰运动,也会对功率的波动产生一定的影响。Wright[5]研究了在选定工作点下非线性模型线性化后的状态空间反馈控制,并且设计了一种扰动调节控制器,通过附加状态估计器估计风的扰动来抑制扰动的影响并减小了平台的运动。此外,线性二次调节器、线性参数变化、模型预测控制和前馈控制[6-8]等方法也都用于减小海上浮式风机的平台运动。

当风机尺寸逐渐增大时,由于转子平面[9]上的风速变化,风机的叶片也受到不对称或周期性变化的负荷。造成这个影响的因素很多,如风机叶片经过塔时存在塔影效应[10]。另一个因素是风切变,这是由于在大气中相对较短的距离上风速或风向的差异造成的。叶片也受到不对称或周期性变化的负荷会严重影响其使用寿命,单独桨距控制方法可以解决这个问题,其每个叶片的桨距角是单独控制的。Bossanyiti[9]提出了独立变桨控制策略可以显著地减小风机叶片的载荷。Laks等[11]使用单独桨距控制与基于预测风干扰的前馈方法相结合,实现负载缓解。Suemoto等[12]在单独桨距控制控制器设计中利用多叶片坐标变换,从线性周期系统中获得合适的线性定常系统,采用显式模型预测控制设计了转矩控制器,在保持有良好的功率调节的基础上,同时有效的降低了叶片疲劳负荷。

上述控制系统开发通常建立在风机的动力学模型的基础上。然而风力发电机组运行环境复杂,动力学模型具有高度非线性和参数不确定性。由于控制设计中所使用的标称模型通常是在特定的运行点进行线性化处理获得的,因此在风速发生变化时,风机的动力学模型会出现较大的不确定性。此外,当系统的状态发生变化时,风机的动力学模型也会出现变化。因此,这些系统的不确定性会影响控制方法的准确性和可行性,一般的解决办法是对不同的状态的风机进行线性化后设计参数,对于不同状态的风机控制策略使用不同的增益参数进行调节,然而这样会导致这些方法在设计时调整参数复杂且需要更多的风机系统模型的知识。

针对非线性的风机系统,规定性能控制方法对于误差跟踪具有良好的性能,在不需要精确的动力学模型得同时,可以保持良好的瞬态和稳态性能。Zhang[13]结合规定性能控制方法和反步技术,以简单的形式构造了控制器,使跟踪误差渐近收敛于零而不需要姿态控制系统动力学的任何相关信息。规定性能控制方法可以使跟踪误差收敛到预设值,但设计参数与收敛率之间的数学关系难以确定。而有限时间规定性能方法可以很好地解决上述问题。Sun等[14]提出了一类具有外部扰动的严格反馈非线性系统的事件触发鲁棒模糊自适应规定性能控制策略。该控制方法定性地确定了设计参数与收敛速度之间的关系,同时保证了半全局的稳定性,跟踪误差在有限时间内收敛到一定范围内。

本文结合规定性能方法设计了统一桨距控制和单独桨距控制的控制器并结合两者控制风机的功率和减少风机结构的疲劳载荷,最后在FAST平台进行仿真,并与GSPI方法进行比较,仿真结果表明本文的方法在保持额定功率的同时减小平台的俯仰运动和风机的叶片载荷上有良好的效果。

1 风机系统模型

本文选择了NREL 5MW OC3- Hywind浮式风机[15]。该风机采用广泛使用的风机仿真软件FAST[16]进行仿真。FAST可提供几十个自由度,包括塔、叶片和平台的运动、转子的旋转、偏航运动,这些模型对于控制设计来说过于复杂,本文的控制设计只考虑2个自由度：平台的俯仰角和风轮的转速,建立简化的二自由度模型[17]：

(1)

对风机的二自由度模型进行简化得：

(2)

式中：f(x,t)=A(t)·x+Bd(t)·δ;g(x,t)=B(t),且f(x,t)和g(x,t)是未知且有界的。

本文设计的控制器的主要目的是限制功率在其额定值,减少平台俯仰运动和衰减叶片根部的挥舞力矩。前2个目标可以通过统一桨距控制实现,而第3个目标可以通过单独桨距控制实现。为了简化控制设计,本文使用简化模型设计了控制器,然后后续的仿真试验是在FAST平台上进行的。

2 问题描述

本文使用统一桨距控制实现限制功率在其额定值减少平台俯仰运动,通过单独桨距控制控制实现衰减叶片根部的挥舞力矩。

2.1 CPC的问题描述

在额定风速之上,风力发电机的控制目标为保持功率的恒定并且减小平台的运动,一般是保持额定的扭矩T0,通过调节桨距角β来保持风轮转速ω跟踪额定转速ωr以保持功率恒定,额定转速ωr为：

(3)

式中：P0为风力发电机的额定功率;ng为齿轮箱的传动比。

但是上述控制目标只能保持输出功率的稳定问题,不能减小平台的俯仰运动,为了减小平台的运动,可以更改风轮转速的控制目标,即把平台的俯仰角速度加入到预期风轮转速的设计中,新的预期风轮转速为[4,18]

(4)

2.2 单独桨距控制的问题描述

由于风切变,塔影效应和湍流风的影响,转子平面上的风速发生变化,导致风机的叶片会受到不对称或周期性变化的负荷[9-10]。非对称载荷会严重影响风力机的使用寿命。单独桨距控制方法单独的控制每片桨叶的桨距角,可以有效地解决这个问题。

如图1所示,单独桨距控制系统由3层结构组成：科尔曼变换、载荷控制和逆科尔曼变换。

图1 整个闭环系统的控制方案Fig.1 Control scheme of the whole closed-loop system

科尔曼变换过程是使用转子方位角ψ将3个叶片根部挥舞力矩M1、M2、M3转化为轮毂处的倾斜力矩Mtilt和偏航力矩Myaw[9]：

(5)

载荷控制的目的为减小集体倾斜力矩Mtilt和偏航力矩Myaw,并且这2个载荷可以通过2个单输入单输出的控制器进行控制达到减小载荷的目的[9]。βtilt、βyaw为控制输出,对βtilt、βyaw进行逆科尔曼变换生成每个桨叶的额外桨距角输入Δβ1、Δβ2、Δβ3。

(6)

3 控制器设计

3.1 有限时间规定性能控制方法

定义1[19]一个光滑函数ρ(t)称为有限时间性能函数,当它满足下列性质：

1)严格递增的、可逆的函数;

4)当t≥T0时,ρ(t)=ρ∞,T0为给定的时间。

有限时间性能函数：

(7)

式中：ρ0为性能函数初始值;ρ0要大于初始误差;ρ∞为设计的收敛值;T0为设计的收敛时间;ρ0、ρ∞和T0为设计的正常数。

对跟踪误差进行误差转换,首先利用性能函数建立误差的约束条件：

(8)

定义一个函数M(s),它具有以下属性：

1)平滑的、严格递增的、可逆的函数;

建立符合条件的M(s)函数：

(9)

误差转换过程为：

e(t)=ρ(t)M(s)

(10)

对式(10)取反函数得：

(11)

求式(11)的时间导数得：

(12)

对于简化的二自由度系统：

(13)

建立跟踪误差：

e=x-xd

(14)

基于式(11)设计控制律：

(15)

式中k1、k2为设计的正常数。

选取一个Lyapunov函数证明系统的稳定性：

(16)

对式(16)求时间导数并把式(15)代入得：

(17)

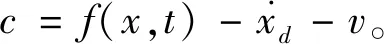
利用杨氏不等式,不等式成立：

(18)

把式(18)代入式(17)得：

当r1<0有,s收敛于：

(19)

当s有界时,约束不等式(8)成立,跟踪误差收敛到约束范围内。最后,根据规定性能函数的定义,参数ρ0、ρ∞和tf应该根据实际的要求进行选择。特别是参数ρ0需要大于系统的初始跟踪误差。为了满足s有界,需要选择合适的增益参数k1和k2满足不等式r1<0。

3.2 有限时间规定性能控制方法用于变桨控制

风轮转速跟踪误差：

(20)

基于式(15),统一桨距控制方法的控制输入为：

(21)

单独桨距控制方法用于减小集体倾斜力矩Mtilt和偏航力矩Myaw,把Mtilt、Myaw定义为误差输入：

(22)

控制目标为使得Mtilt、Myaw趋近于零,基于式(15),控制输入βtilt、βyaw为：

(23)

对βtilt、βyaw进行逆科尔曼变换生成每个桨叶的额外桨距角输入Δβ1、Δβ2和Δβ3,与统一变桨控制输入结合生成每个桨叶的桨距角输入：

(24)

4 仿真结果

本文利用FAST对NREL 5MW OC3-Hywind浮式风机进行仿真试验,Dagher等[20]通过对比试验结果和仿真试验结果验证了FAST对NREL 5MW OC3-Hywind浮式平台风机的仿真能力。桨距角的调节速度限制为±8°/s。下面的仿真中使用了2个控制器。

GSPI：一种增益调度PI控制方法[3]。

FTPP-IPC：将FTPP方法用于IPC,控制输入为式(24)。

GSPI控制器的控制输入定义为：

(25)

式中：KP(βr)和KI(βr)为变增益参数,会随桨距角的变化而变化,KP(βr)和KI(βr)定义为：

(26)

仿真环境如下：

工况1：风为18 m/s的湍流风;不规则波显著高度为3.25 m,峰谱周期为9.7 s。

工况2：风为21 m/s的湍流风;不规则波显著高度为4 m,峰谱周期为9.7 s。

性能函数的参数选择如表1～2所示,控制参数的选择如表3所示。

表1 统一变桨控制的性能函数Table 1 The performance function parameters of CPC

表2 独立变桨控制的性能函数Table 2 The performance function parameters of IPC

表3 控制器参数Table 3 The controller parameters

图2为不同工况下风轮转速,表4为风轮转速与额定转速差的均方根,可以明显看出,在2种工况下,相比于GSPI方法,基于FTPP的方法的跟踪误差更小,FTPP-IPC方法的转速跟踪误差的均方根分别减小了52.1%和48.9%。图3为不同工况下2种方法的桨距角变化曲线,为了实现更好的功率稳定性能,基于FTPP-IPC的方法桨距角的调节的变化率要更高一些,基于FTPP-IPC的方法更加充分的发挥了桨距执行器的性能,同时也会加重桨距执行器负担,但是2种方法的桨距角的调节速率都在限制范围之内,所以这个问题不影响该方法的使用。

表4 跟踪误差的均方根Table 4 RMS of tracking error

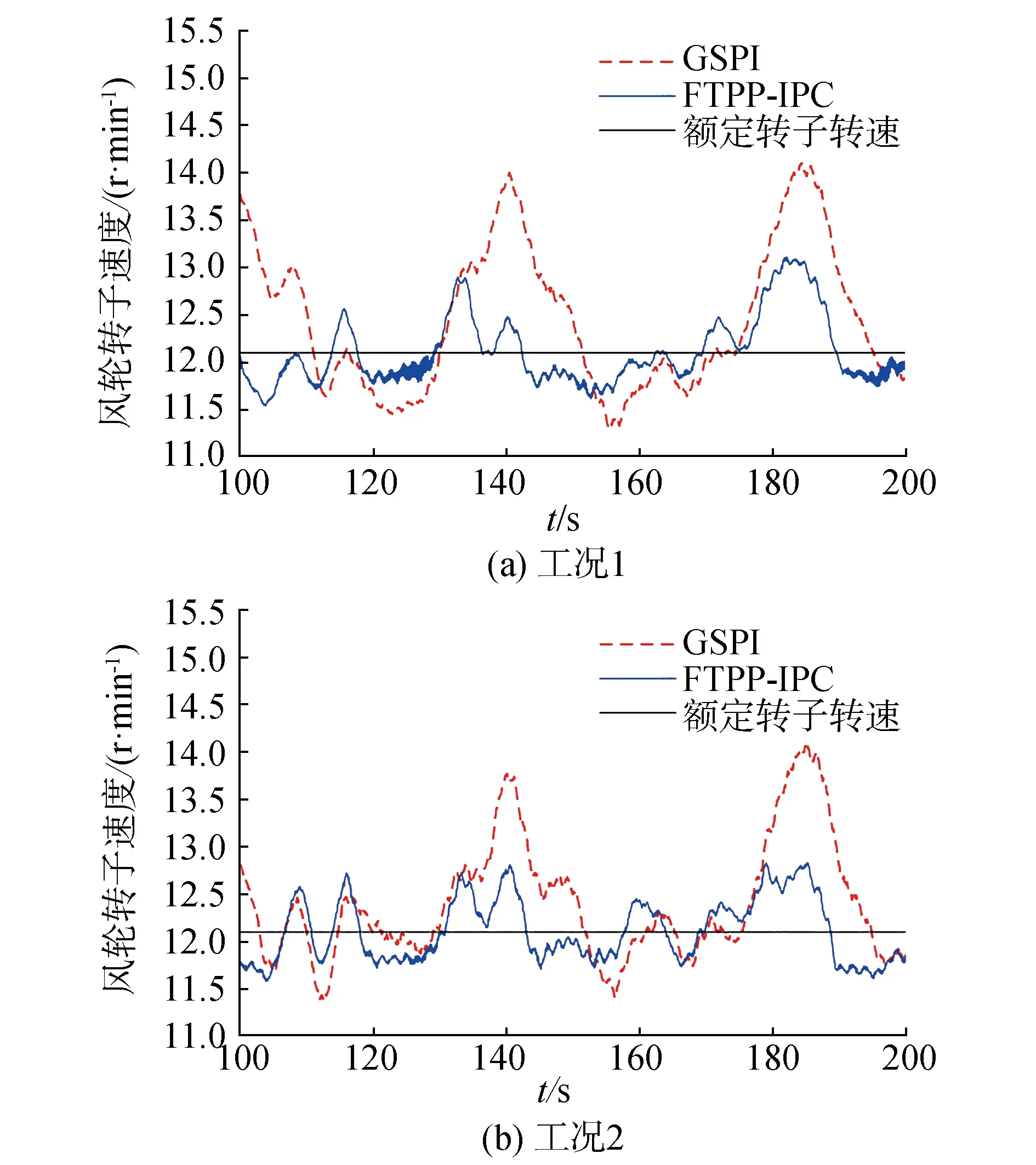
图2 风轮转子转速Fig.2 Rotor speed

图3 叶片桨距角曲线Fig.3 Curves of Blade pitch angles

图4为2种工况下平台的纵摇运动,相比于GSPI,FTPP-IPC方法减小了平台纵摇运动响应的波动范围。表5为2种工况下平台纵摇运动的均方根,由表可知在2种工况下,相比GSPI,FTPP-IPC方法的平台纵摇运动响应的均方根分别减小了8.3%和9.7%,FTPP-IPC方法可以有效的减小平台的纵摇运动。