基于径向基函数神经网络的空间漂浮机械臂装配控制

刘育强,魏庆生,李浩然,魏承,赵阳

(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001;2.北京空间飞行器总体设计部,北京 100094)

目前航天器正在向大型化、模块化方向发展,在轨装配作为空间操作技术的一种[1],对未来大型航天器的在轨装配、模块更换及维修有重要意义。空间机械臂作为一项较为先进的装配手段已经成为各国的研究焦点[2]。加拿大的SRMS和SSRMS机械臂已经部署到国际空间站中,对空间站的建设和日常维护起到了重要作用[3]。欧空局(European Space Agency,ESA)研制的欧洲机器人手臂(European robotic arm,ERA)[4]部署在国际空间站俄罗斯舱段,主要负责在轨装配和模块更换。中国的空间机械臂[5]也已完成地面试验,未来将应用于“天宫”系列空间站的各项舱外任务[6]。

利用空间漂浮基座机械臂进行在轨装配需要机械臂控制系统具有良好的控制性能,尤其在航天器模块日益精密和复杂的趋势下,对于装配性能的要求更加苛刻。空间漂浮基座机械臂本身是一个非线性系统,动力学特性复杂,而且在实际装配过程中由于关节摩擦及柔性的存在[7],导致本身动力学模型失准,以及在面对不同装配模块时,目标物的质量惯量等动力学参数缺失的情况下,都要求控制系统具有良好的鲁棒性[8]。对此,学者们将鲁棒控制算法[9]、自适应控制算法[10]、模型预测控制算法[11]、LQR最优控制[12]等应用到空间机械臂在轨装配技术中,取得了良好的效果。由于径向基函数神经网络(radial basis function neural network,RBFNN)有很好的非线性逼近能力[13],可以适用于空间装配中动力学模型参数不准确的情况,目前已被用于其他复杂的非线性系统的控制当中[14-15],基于神经网络的控制系统可以满足复杂空间装配任务的需要。但完全依赖无模型的神经网络的控制容易出现过拟合、欠拟合、计算量大[16]的现象,因此考虑将基于模型和神经网络补偿结合起来,由径向基函数神经网络补偿模型的不确定部分,再由基于模型控制进行控制,实现既能在目标参数位置的情况下满足控制指标,又能结合动力学模型先验知识提升计算效率。

本文针对空间漂浮基座机械臂在轨装配问题,首先给出空间漂浮基座机械臂的构型设计及动力学模型描述,而后设计了一种基于径向基函数神经网络补偿控制率,使得机械臂末端执行器在未知特性的大负载作用下能够稳定收敛地跟踪期望轨迹。接着设置仿真环境与参数,通过仿真对比实验验证了基于计算力矩法的径向基函数神经网络补偿控制方法的有效性。本文所提出的方法具有较强的工程实用价值,能够为未来的空间装配任务提供借鉴。

1 空间漂浮基座机械臂动力学建模

1.1 空间漂浮基座机械臂构型设计

本文研究的在轨装配过程如图 1所示,由漂浮基座卫星搭载七自由度机械臂接近被装配模块,机械臂的构型参数及物理特性参数如表 1所示,再由空间装配机械臂末端执行器卡具连接六角形被装配模块,在控制器的作用下,实现被装配模块的装配和移动。

1.2 空间漂浮基座机械臂动力学建模

采用空间算子代数方法对空间漂浮基座机械臂进行动力学建模为：

(1)

图1 空间漂浮基座机械臂在轨装配示意Fig.1 Schematic diagram of D-H coordinate system of seven-degree-of-freedom floating manipulator

表1 七自由度机械臂构型参数Table 1 Configuration parameters of seven-degree-of-freedom manipulator

2 基于RBFNN的补偿控制率设计

2.1 控制器设计

将无外力作用下空间漂浮基座机械臂的理想动力学模型简写为：

(2)

在实际模型中,会存在干扰力矩和摩擦等因素,因此空间漂浮基座机械臂的实际动力学模型将变为：

(3)

式中：τr表示所有外界不确定因素产生的干扰力矩总和。设状态跟踪误差为：

(4)

式中qd和q分别表示期望的和实际的广义坐标。基于计算力矩法控制律为：

(5)

将式(3)代入到式(5)中得：

(6)

(7)

基于估计的动力学模型设计的控制律为：

(8)

将式(5)和式(7)代入式(8)得：

(9)

式(9)右侧的部分为非线性项,设：

(10)

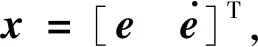
(11)

由神经网络特性可知,必存在极小的正数ε0和权值矢量W*,使得：

(12)

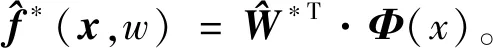
定义逼近误差为：

η=f(x)-f*(x,w)

(13)

假设逼近误差有界,临界值为：

(14)

综上,可得到完整的控制律为：

τmodel+τRBF

(15)

通过控制律设计,可以得出总体控制思想为采用计算力矩方法对已知模型进行有效控制,采用RBFNN对模型的不可知部分进行补偿,该方法可以合理地减轻控制系统运行负担,避免全部采用RBFNN计算造成的计算效率低下问题[16],从而达到实际要求的快速精确的控制目的。整体控制思想如图 2所示。

图2 基于计算力矩法的RBFNN补偿控制结构Fig.2 RBF neural network compensation control structure based on calculating torque method

2.2 自适应律设计与稳定性收敛性分析

对前述设计的控制律式(15),根据Lyapunov理论进行稳定性与收敛性分析。

(16)

(17)

(18)

(19)

将式(19)代入式(18)可得：

(20)

设Lyapunov函数为：

(21)

式中γ>0。

矩阵P是对称正定的且满足Lyapunov方程：

PA+ATP=-Q

(22)

式中Q≥0。

定义

(23)

式中tr(·)为矩阵的迹,则：

(24)

对式(21)左右两侧求导,得：

(25)

又有

(26)

将式(26)代入式(25)得：

ηTBTPx

(27)

设计自适应律[17]为：

(28)

则：

(29)

(30)

由前面可知,‖ηT‖≤‖η0‖,‖B‖=‖I‖,则：

(31)

式中：λmax(P)为矩阵P的最大特征值;λmin(Q)为矩阵Q的最小特征值。

(32)

即：

(33)

由此可见,若想提高x的收敛效果,可以减小λmax(P),增大λmin(Q),或者减小η0。

3 仿真结果及分析

3.1 仿真参数设计

本文仿真案例基于航天器在轨模块装配任务,由漂浮基座服务航天器搭载七自由度空间机械臂,抓持模块进行装配,连接方式为机械臂末端卡具固定。规划了2阶段期望轨迹,阶段1从(-0.3,0,2.532)运动至(-0.3,0,1.7),阶段2再运动至(0.6,0.5,1.9),均为直线轨迹,期望的关节角速度和角加速度规划均采用五次多项式规划。

控制器的设计为了对比验证所设计的RBFNN补偿控制器的有效性,分别采用无RBFNN控制补偿和有RBFNN控制补偿2种进行仿真分析。分为3个工况,分别为：1)机械臂无负载;2)机械臂采用无补偿模式控制500 kg的模块进行装配;3)机械臂采用RBFNN补偿模式控制500 kg的模块进行装配。

仿真环境采用Matlab/Simulink与MBDyn[18]联合仿真。各仿真参数见表 2和表3。

表2 动力学仿真参数Table 2 Dynamic simulation parameters

表3 控制器仿真参数Table 3 Controller simulation parameters

3.2 仿真结果分析

得到仿真结果如图3～5所示。

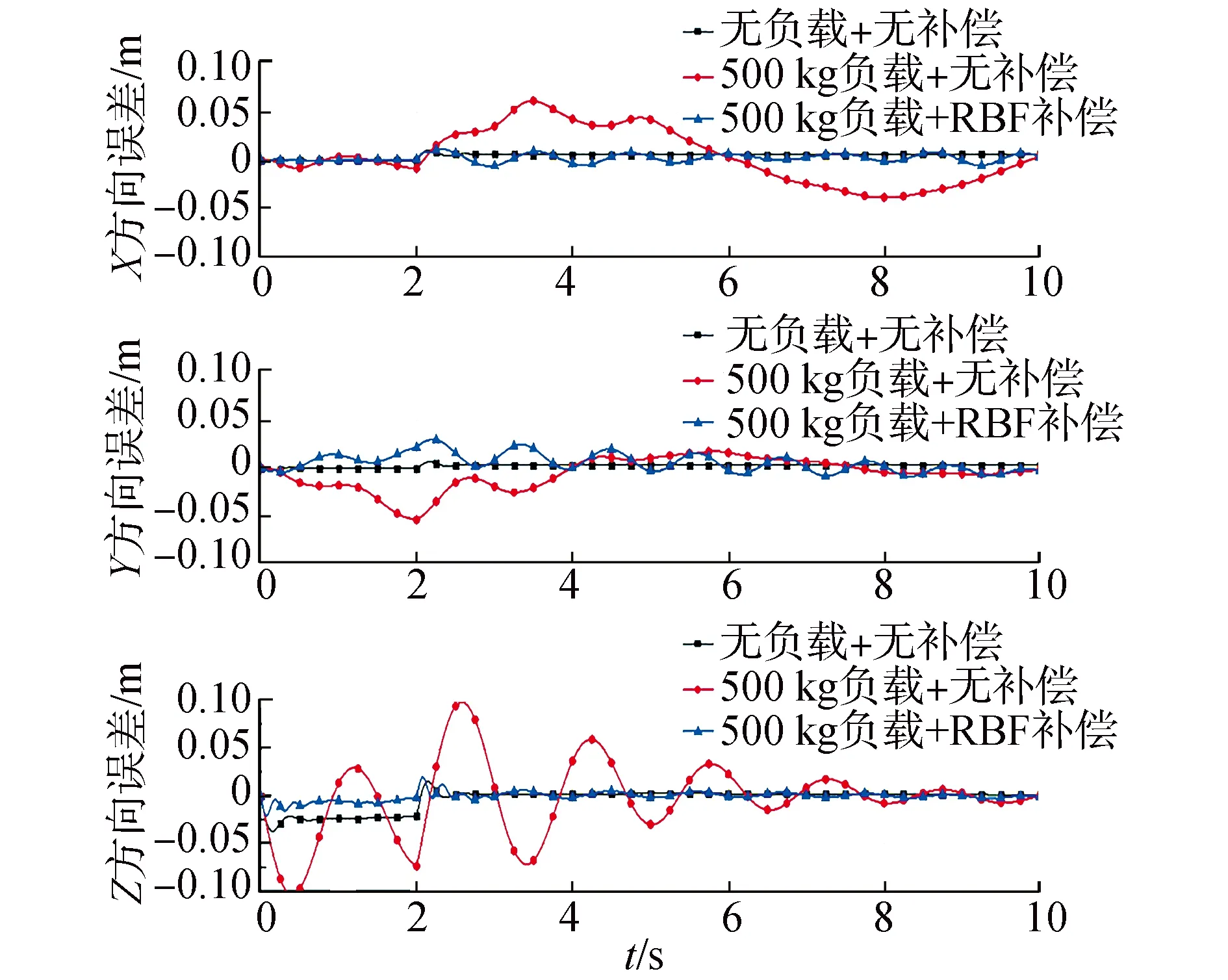
图3 模块装配过程中各方向位置误差Fig.3 Position error in all directions during module assembly

图3和图4分别表示模块在机械臂装配操控下x、y、z方向上的位置误差与空间轨迹。可以看出,在工况1机械臂空载时,机械臂末端能够较好地跟踪期望轨迹,在阶段1启动时,跟踪具有一定的迟滞性,导致沿运动方向的z方向误差达到0.025 m,但是能够较快地收敛,跟踪效果较好。同时虽然是基于模型的控制,但是由于关节摩擦力矩的存在,模型的实际值与参考值有一定偏差,还会存在一定的稳定误差,但在工况1中较小。

图4 模块装配过程中轨迹显示Fig.4 Track representation during module assembly

在工况2中,由于机械臂末端连接了质量为500 kg的模块(对于控制系统质量未知),通过图5可以看到,x、y、z3个方向的跟踪误差较大,特别是z方向的误差最大达到了0.1 m,并且在阶段1和阶段2切换时震荡明显,且收敛速度慢,这是由于实际动力学模型与参考值相差过大,控制器性能下降甚至导致发散。在实际任务中容易发生模块与航天器碰撞的事故,对于精密模块甚至可能导致损坏。

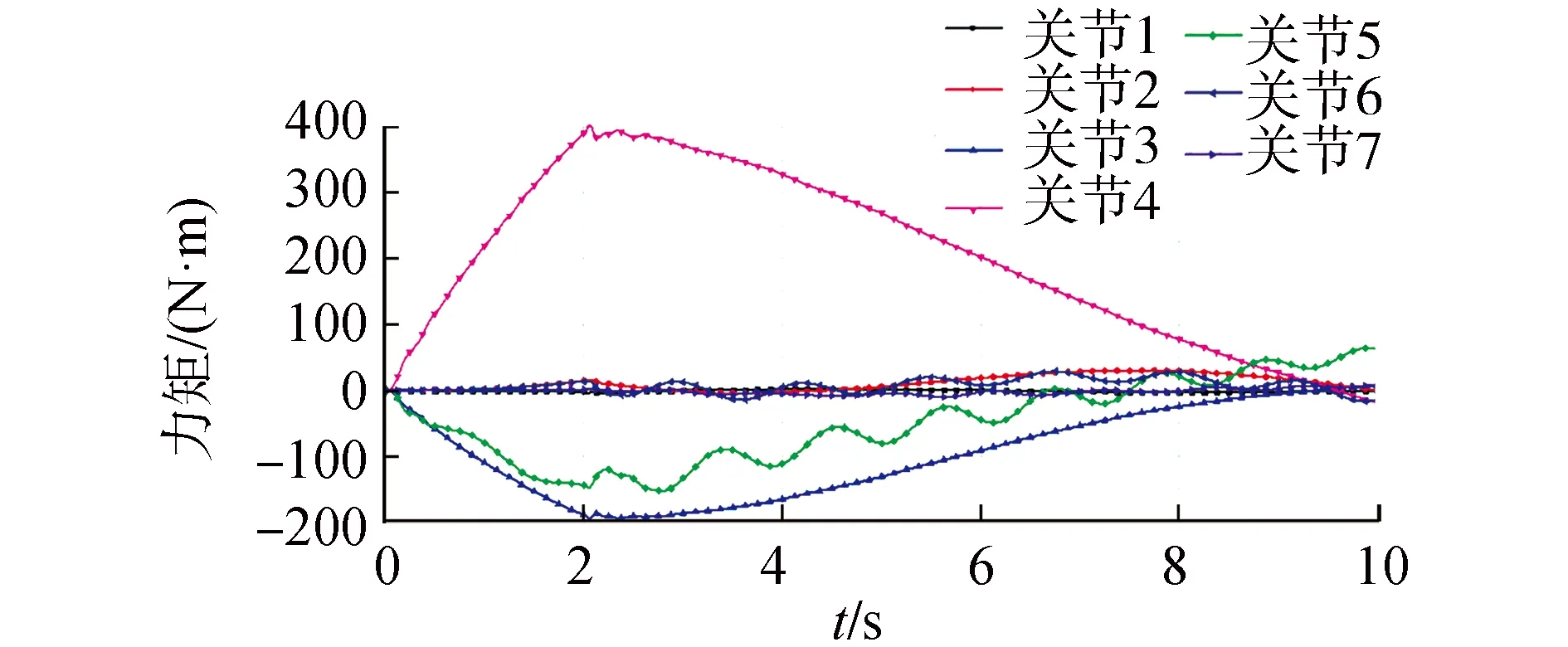
图5 基于RBFNN的各关节补偿力矩Fig.5 Compensation torque of each joint based on RBFNN

在工况3中,由于加入基于RBFNN的控制补偿,模块在阶段1的起始误差就得到了较好的补偿,控制在了0.01 m范围内,且在运动状态切换时也能够及时反应,超调量较小,且能够收敛到0,稳态误差小,相比与没有补偿的工况2,控制性能得到有效提高。

图6反映了基于RBFNN的各关节补偿力矩值,在运动过程中,关节3和关节4补偿值较大,说明在装配过程中关节3、4承担较大的负载,这是由于在z、y方向运动时,关节4作为连接2个大臂的关节,主导着空间中的大范围运动,所产生的力矩也较大,达到400 N·m,并随着轨迹稳定而下降,符合预期。服务航天器基体位置误差在2.3 s时收敛于0,之后一直保持近乎为0的误差,实现了基体位置精确控制;基体速度误差在2.5 s时收敛于0并保持到6 s,6 s以后的波动是因为机械臂系统开始装配零件,造成了系统惯量的变化,但是控制器很快将误差重新收敛于0;基体的姿态四元数误差始终保持为0(10-3量级),姿态控制精度很高。值得一提的是,由于加入RBFNN补偿,神经网络的计算负载较大,导致仿真效率有所下降,比工况1,2用时多40%,这对未来的星上处理器的计算能力以及通讯速度上有着更高的要求。

图6 基于RBFNN的服务航天器位姿误差Fig.6 Service spacecraft position and attitude errors based on RBFNN

4 结论

1)设计了一种基于RBFNN的空间机械臂补偿控制算法,补偿了因为机械臂动力学模型失准和装配物体动力学特性未知等造成的控制误差,并进行了自适应律设计与稳定性收敛性分析,结果证明所设计控制律合理有效。

2)通过搭建仿真程序,对比了采用无RBFNN控制补偿和有RBFNN控制补偿2种控制器下的控制效果,结果表明,在目标动力学参数未知的情况下,带有RBFNN的补偿控制对大负载物体有着更好的控制性能,能够有效地跟踪期望轨迹,控制误差在0.01 m范围内,且在运动状态切换时也能够及时反应,超调量较小,且能够快速收敛,稳态误差小,相比与没有补偿的条件下,控制性能得到有效提高,可以用于未来的各项在轨装配任务。