生育率与经济发展

喻胜华 赵盼

［摘 要］ 选取全球150个国家（或地区）的数据，采用两种不同的分类方法，将样本划分为7个不同的子样本，基于分位数回归方法探究生育率与经济发展之间的关系。实证结果表明，只有当经济发展达到一定水平时，生育率与经济发展之间才会出现反向“J”型关系，这种关系不仅与经济发展水平相关，也与生育率水平相关。反向“J”型模式中的斜率虽然为正，但斜率较小。

［关键词］ 生育率；经济发展；反向“J”型关系；分位数回归

［中图分类号］ F063.4 ［文献标识码］ Ａ ［文章编号］ 1008—1763（2023）01—0058—08

Fertility Rate and Economic Development

——An Empirical Study Based on Quantile Regression

YU Sheng-hua， ZHAO Pan

（School of Economics and Trade， Hunan University， Changsha 410079， China）

Abstract：The data of 150 countries （or regions） in the world were selected， and the samples were divided into 7 different subsamples by two different classification methods. The relationship between fertility rate and economic development was explored based on the quantile regression method. The empirical results show that only when the economic development reaches a certain level， there will be a reverse “J-shaped” relationship between fertility rate and economic development， which is not only related to the level of economic development， but also to the level of fertility rate. In the reverse “J” pattern， the slope is positive but small.

Key words： fertility rate；economic development；reverse J-shaped relationship；quantile regression

一 引言及文献综述

在全球经济取得空前增长的同时，人类的生育率却经历了大幅度的下降。根据世界银行公开的数据，从1960年到1964年，世界总和生育率经过了短暂的小幅上涨之后持续下降，到2019年已降为2.403，但仍高于更替水平（2.1）。而反观我国，在1960年，我国的总和生育率为5.756，此时，我国的总和生育率远高于世界平均水平。从1960年到1965年，我国的总和生育率经历了小幅上涨，之后迅速下滑，到1992年，我国的总和生育率已跌破更替水平，降至1.977。自1992年以来，我国的总和生育率一直处于更替水平之下。2013年，我国的“单独二孩”政策正式开放，2016年，“全面二孩”政策开始正式实施。然而，近年来，我国的总和生育率并没有随生育政策的放松而显著提升。经济迅速发展的同时，伴之而来的似乎是总和生育率的持续下降。

学者们针对生育率与经济发展之间的关系展开了广泛的研究，其研究结论大致有如下四种：一是生育率与经济发展之间存在负相关关系，该结论得到了学界的普遍认同。如Chen J等使用1990年和2000年的中国人口普查数据以及2005年的小型人口普查数据，分析了1975年至2005年间经济发展和生育政策对广东省生育率下降的影响，结果表明，经济发展带来了城市和农村居住、教育等方面的巨大变化，也极大地促进了广东省生育率的下降^[1]。Kitaura K和Yakita A认为，在经济增长过程中，每个孩子的教育成本会增加，生育率会下降^[2]。Zakaria M 等使用1972-2013年的面板数据，分析了孟加拉国、不丹、印度、马尔代夫、尼泊尔、巴基斯坦和斯里兰卡7个南亚国家的生育率，认为南亚地区的生育率随经济发展水平的提高而下降^[3]。Madsen J B等基于92个发展中国家1960-2014年间的数据，发现人均收入的增加是发展中国家生育率下降的重要决定因素之一^[4]。Gtmark F和Andersson M分析了欧洲东部、欧洲西部、阿拉伯国家等全球6个区域141个国家的相关数据，发现生育率与人均GDP呈负相关关系^[5]。二是生育率与经济发展之间的负相关关系在不同的经济发展阶段存在异质性。比如，Furuoka F采用阈值回归方法分别研究了总和生育率与人均GDP之间的关系以及生育率和人类发展指数之间的关系，研究表明，当收入水平低于阈值时，总和生育率与人均GDP之间存在显著的负相关关系，当收入水平超過阈值时，总和生育率与人均GDP之间的负相关关系也不会逆转为正相关关系。在人类发展指数较低的国家，生育率和人类发展指数之间存在强烈的负相关关系，在人类发展指数较高的国家，生育率和人类发展指数之间虽然也存在负相关关系，但这种负相关关系相对较弱^[6-7]。三是生育率与经济发展之间存在正相关关系，该结论只是个别学者的观点。如Brueckner M和Schwandt H基于1960-2007年间139个国家的面板数据，通过控制国家和时间固定效应，研究了人均GDP与人口增长率之间的关系，结果表明，人均GDP每增加1个百分点，各国的人口增长率就会增加约0.1个百分点^[8]。四是在不同经济发展阶段、不同地区，生育率与经济发展之间存在完全相反的相关关系。Myrskyl? M等率先发现之前被学者们广泛接受的总和生育率和人类发展指数之间的负相关关系发生了变化，即在人类发展指数处于低、中水平时，总和生育率随着人类发展指数的增加而下降，当人类发展指数处于高水平时，进一步的发展可以扭转总和生育率下降的趋势，此时，总和生育率随着发展水平的提高反而开始上升^[9]。该研究结论引发了学者们的热烈讨论：之前被广泛接受的总和生育率与发展水平之间的负相关关系是否变成了反向“J”型关系？Dominiak P等使用1970-2011年间18个国家的面板数据分析了总和生育率与经济增长之间的关系，认为总和生育率先随着经济增长而下降，而后会随经济增长而上升^[10]。Luci-Greulich A和Thévenon O研究了1960-2007年间OECD国家的经济发展对生育率的影响，结果表明，总和生育率与经济发展之间的强负相关关系不再成立，相反，当经济发展到某一临界水平时，这种强负相关关系会变成正相关关系^[11]。Ohinata A和Varvarigos D研究了人口转型与经济发展中的生育率反弹，认为当经济发展到后期阶段，经济增长过程会产生足够的资源，使每个家庭可以抚养更多的孩子，同时也能为每个孩子提供理想的教育投资，从而会出现生育率反弹^[12]。Fox J等通过调查1990-2012年间欧洲256个地区的数据发现，在许多地区内，生育率与经济发展之间的负相关关系正在减弱，而在一些地区中可以观察到负相关关系逆转的趋势^[13]。

现有研究多是对部分国家或部分地区的生育率与经济发展之间的关系进行分析，鲜有从全球视角出发，对不同发展水平国家的总和生育率与经济发展之间的关系进行深入探讨；另一方面，从研究方法来看，现有研究多使用传统的均值回归方法及其相关的最小二乘估计，该方法所能反映的信息量往往是相对有限和狭隘的，且其假设条件在实际应用中经常无法满足。为此，本文主要做了如下工作：一方面，试图从全球视角出发，选取了全球150个国家（或地区）的数据，并使用更深入、更详细、更均匀的分类方式，将150个国家（或地区）的相关数据分为7个子样本，在此基础上研究生育率与经济发展之间的关系；另一方面，在基准回归模型的基础上，引入了分位数回归模型，探索生育率与经济发展之间是否存在反向“J”型关系。如果二者之间存在反向“J”型关系，则进一步探索二者之间的反向“J”型关系是否与生育率水平相关。

二 机理分析

（一）生育率和经济发展负相关的经济学解释

Becker G S和Barro R J提出了一种分析生育率的理论框架^[14-15]，该理论框架被称为“新家庭经济学理论”，它为解释生育率和经济发展之间存在负相关关系提供了主要的理论依据。该理论将孩子视为一种正常品，认为生育需求的收入效应和替代效应的权衡决定了生育率的高低。随着经济的发展，女性的收入增加，进而会促使更多女性参与劳动。在不能将工作和养育孩子平衡时，如果待在家里照顾孩子，则意味着女性工资的损失，这种损失是女性生育孩子的间接成本。因此，女性就业和生育率之间为替代效应。基于该理论，Sprague A认为，女性劳动参与度的提高以及女性工资的提升使得生育的影子价格提升，从而导致了生育率的下降^[16]。

Becker G S等基于新家庭经济学理论，从孩子数量和质量之间相互作用的角度解释了生育率的下降。他们研究了在家庭收入不变的约束下，在孩子数量和孩子质量之间进行权衡，以实现家庭效用函数的最大化^[17]。在现代社会中，随着经济的发展，为了应对新的经济现实和社会需求，父母会更注重提高孩子的质量。对于父母而言，孩子质量的提高需要付出更多的成本，所以会倾向于减少孩子的数量，进而导致了生育率的下降。

（二）生育率和经济发展负相关关系逆转的理论分析

生育率与经济发展之间的关系在理论和实证上仍是不明确的，虽然它们之间的负相关关系被多数学者所接受，但也受到了一些学者的质疑，认为二者之间的负相关关系并不总是会保持，而是可能会发生逆转，甚至会表现为正相关关系。

根据新家庭经济学理论，在家庭中，当女性不得不在参加工作和抚养孩子之间做出选择时，才会导致生育率下降。但是，如果女性能进入工作岗位，同时也能兼顾抚养孩子，随着经济的发展，女性的工资也会随之增加，高工资使之更容易负担抚养孩子的成本，此时女性的工资不仅仅为替代效应，其收入效应可能开始占主导地位，经济发展和女性就业对生育率的负向影响可能会减弱^[18]。

最近几年，在一些发达国家中，偏向技能的技術变革增加了技能溢价，因此降低了儿童保育服务的相对价格，而女性平均工资的增加使育儿成本变得更容易承受。因此，经济发展和女性工资对生育率的影响可能会由负向逆转为正向^[19]。Luci-Greulich A和Thévenon O进一步指出，在一些高度发达的国家，如果能提高女性就业和生育的兼容性，则经济发展和生育率之间的负相关关系会出现逆转，表现为反向“J”型关系。但如果经济发展过程中，没有相应的制度变革，以提高父母把工作和家庭生活结合起来的可能性，那么生育率增长的可能性将很小^[11]。

近几十年来，不少发达国家实施了不尽相同的家庭政策，虽然各国实施的家庭政策不尽相同，但鼓励生育是其中的一个重要目标。很多政策均有助于降低家庭抚养孩子的机会成本，也有助于儿童保育。比如，家庭政策中的育儿假计划可以保证父母在休假一段时间后返回到以前的工作岗位，减少了未来职业选择的不确定性；家庭政策中，公共儿童保育服务的改善可以解决父母忙于工作而无法抚养孩子的后顾之忧，提高父母工作和生育的兼容性，从而降低了父母生育孩子的机会成本。还有一些家庭政策会给予育儿补贴或减免税收等。这些家庭政策均不同程度地降低了家庭生育孩子的机会成本，有助于削弱生育率和经济发展之间的负相关关系，甚至有可能将两者之间的负相关关系扭转为正相关。

互联网技术的飞速发展为人们创造了比之前更灵活的工作安排，在这种情况下，员工不需要在所有工作时间都在正常工作场所出现。随着经济的发展，技术进步正改变着21世纪经济活动的空间组织。在此过程中，相对灵活的工作安排可以将抚养孩子和工作相结合，这对家庭的生育决定产生了积极的影响，有助于逆转经济发展与生育率之间的负相关关系^[20]。除经济因素外，也有学者从移民等其他角度解释了生育率逆转。

三 研究设计

（一）样本分类方法

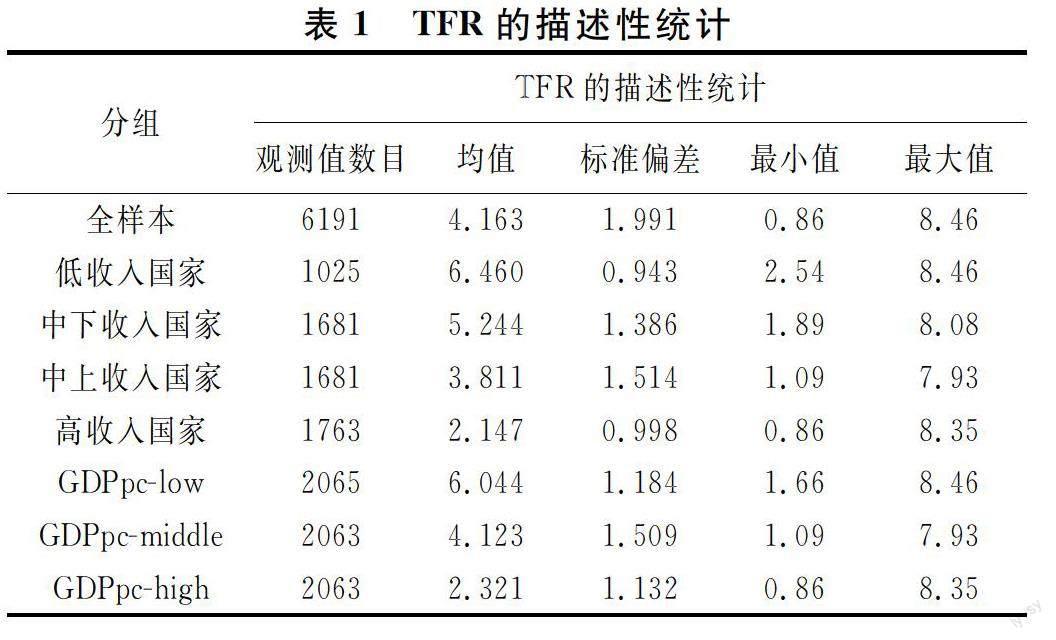
总和生育率（TFR）反映了女性一生中生育孩子的总数，是最重要的人口指标之一。本文使用总和生育率作为生育率的指标，其数据来源于世界银行公开数据。经济发展用人均GDP（GDPpc）来衡量，其数据来自宾夕法尼亚大学世界表（Penn World Table，PWT）。鉴于有些国家（或地区）某些年份的数据不完整，我们选取了全球150个国家（或地区）1970-2010年的数据。

本文根据2010年各国人均国民收入，将150个国家（或地区）分为高收入国家、中上收入国家、中下收入国家、低收入国家4个子样本，然后分别研究这4个子样本中不同国家的总和生育率与经济发展之间是否存在反向“J”型关系。此外，将样本按照人均GDP的不同均等地分为低、中、高3个子样本，分别用GDPpc-low、GDPpc-middle、GDPpc-high表示。值得注意的是，在该分类中，同一个国家在不同时期可能属于不同的子样本。以我国为例，1970年，我国的人均GDP是361美元，属于GDPpc-low这一子样本，然而，2010年我国的人均GDP达到了4628美元，属于GDPpc-middle这一子样本。

（二）变量的描述性统计

表1和表2分别报告了全样本和7个子样本的描述性统计结果。

（三）模型设置

由于数据中GDPpc和TFR差距很大，所以，模型中对GDPpc取自然对数。本文使用如下基准回归模型：

其中，αi表示不随时间而变化的个体特征，β0是常数项，ut表示时间效应，εit表示随机误差项。

模型（1）中包含了二次项，如果二次项的系数估计值显著为正，而一次项的系数估计值显著为负，则可以初步认为总和生育率与人均GDP之间的关系在人均GDP达到阈值前是负相关关系，超过该阈值后，它们之间的关系会发生逆转，变为正相关关系，即总和生育率和经济发展之间存在反向“J”型关系。

为了更深入地探索总和生育率与人均GDP之间的反向“J”型关系是否与生育率水平相关，除了使用基准回归模型（1）外，也在基准回归模型（1）的基础上，引入了线性分位数回归模型，如式（2）所示：

其中，QTFRitτln GDPpcit表示总和生育率的条件分位数，模型（2）中的系数会随着分位数τ的不同而发生变化，即为τ的函数。

（四）模型估计方法

首先，针对基准回归模型（1）使用最小二乘法，分别研究全样本以及高收入国家、中上收入国家、中下收入国家、低收入国家、GDPpc-low、GDPpc-middle、GDPpc-high 7个子样本，探讨总和生育率和经济发展之间是否存在反向“J”型关系。

与最小二乘法不同，分位数回归可以通过被解释变量的不同分位数对解释变量进行回归，从而得到被解释变量不同分位数下的回归结果。分位数回归可以提供多条不同的回归曲线，从而对被解释变量在整体分布上的回归做出更清楚的阐释，挖掘的信息量也更加丰富。分位数回归对于变量间的统计关系能描述得更详细、更全面。为此，除了使用基准回归模型外，本文也针对线性分位数回归模型（2），使用分位数回归技术，以进一步探讨生育率和经济发展之间的反向“J”型关系以及反向“J”型关系是否与生育率水平相关。

四 实证结果与分析

（一）基准回归结果与分析

表3给出了基准回归模型（1）的最小二乘回归结果。

由表3易知，对于低收入国家、中下收入国家、中上收入国家、GDPpc-low、GDPpc-middle这5个子样本而言，总和生育率和经济发展之间不存在反向“J”型关系。

对于全样本以及高收入国家和GDPpc-high这2个子样本而言，lnGDPpcit的系数β1的估计值是负的，且在0.01水平下显著。同时，其二次项系数β2的估计值是正的，且在0.01水平下显著，可初步认为，总和生育率和经济发展之间的负相关关系发生了逆转。

为了更准确地判断总和生育率和经济发展之间的关系，我们不仅使用模型（1）的系数β1和β2的估计值，同时也考虑变量的边际效应，即

边际效应的下界、上界及阈值如表4所示。其中，下界和上界是分别根据lnGDPpcit的最小值和最大值计算得到的，而阈值则通过令式（3）的右边等于零计算得到。

由表4易知，对于全样本以及高收入国家和GDPpc-high这2个子样本而言，下界处的边际效应分别为-2.006、-1.376、-0.626，这表明在下界处，总和生育率和经济发展之间存在负相关关系，而上界处的边际效应分别为2.009、2.127、3.365，此时，总和生育率和经济发展之间存在正相关关系。从下界到阈值，总和生育率和经济发展之间是负相关关系，而当GDPpc超过阈值后，它们之间的关系发生了逆转，二者之间的关系转变为正相关关系。可以认为，在全样本以及高收入国家和GDPpc-high这2个子样本中，总和生育率与经济发展之间存在反向“J”型关系。高收入国家和GDPpc-high这2个子样本中TFR和GDPpc的散点图及拟合线分别如图1和图2（太阳花散点图）所示。图中的1个小圓圈代表1个观测值，1朵太阳花代表多个观测值，拟合线是使用局部加权回归散点平滑法得到的。

在图1中，1朵浅色太阳花的每片花瓣代表1个观测值，1朵深色太阳花的每片花瓣代表4个观测值。在图2中，1朵浅色太阳花的每片花瓣代表1个观测值，1朵深色太阳花的每片花瓣代表5个观测值。

根据表3的基准回归结果，并结合表4边际效应的下界、上界以及阈值，可以认为在高收入国家和GDPpc-high这2个子样本中，总和生育率和经济发展之间存在反向“J”型关系，图1和图2进一步证实了这一点。此外，在图1和图2中，绝大多数的浅

色太阳花和深色太阳花分布在反向“J”型图案负斜率的部分，而仅有少部分的小圆圈分布在反向“J”型图案正斜率的部分。也就是说，对于多数观测值而言，TFR和GDPpc之间存在负相关关系，仅有少部分观测值的TFR是随着GDPpc的增加而增加。另一方面，在斜率为正的部分，拟合线倾斜程度较小。这说明，虽然TFR是随着GDPpc的增加而增加，但增加的幅度较小。

（二）分位数回归结果与分析

前面的结论表明，当人均国民收入达到高收入水平或者当人均GDP较高时，总和生育率与经济发展之间的关系才会发生逆转，即二者之间的反向“J”型关系与经济发展水平相关。为此，我们进一步探讨总和生育率与经济发展之间的反向“J”型关系是否与生育率水平相关。

当被解释变量的分布函数是非正态分布时，最小二乘估计不再是一个好的估计。此时，分位数回归技术是一种很好的替代方法，它可以提供一种更稳健的估计。首先对高收入国家和GDPpc-high这2个子样本的总和生育率进行正态性检验，表5给出了相应的检验结果。

由表5可知，高收入国家和GDPpc-high这2个子样本的总和生育率均不服从正态分布。为此，我们针对这2个子样本以及线性分位数回归模型（2），进一步探讨总和生育率与经济发展之间存在的反向“J”型关系以及其反向“J”型关系是否与生育率水平相关。

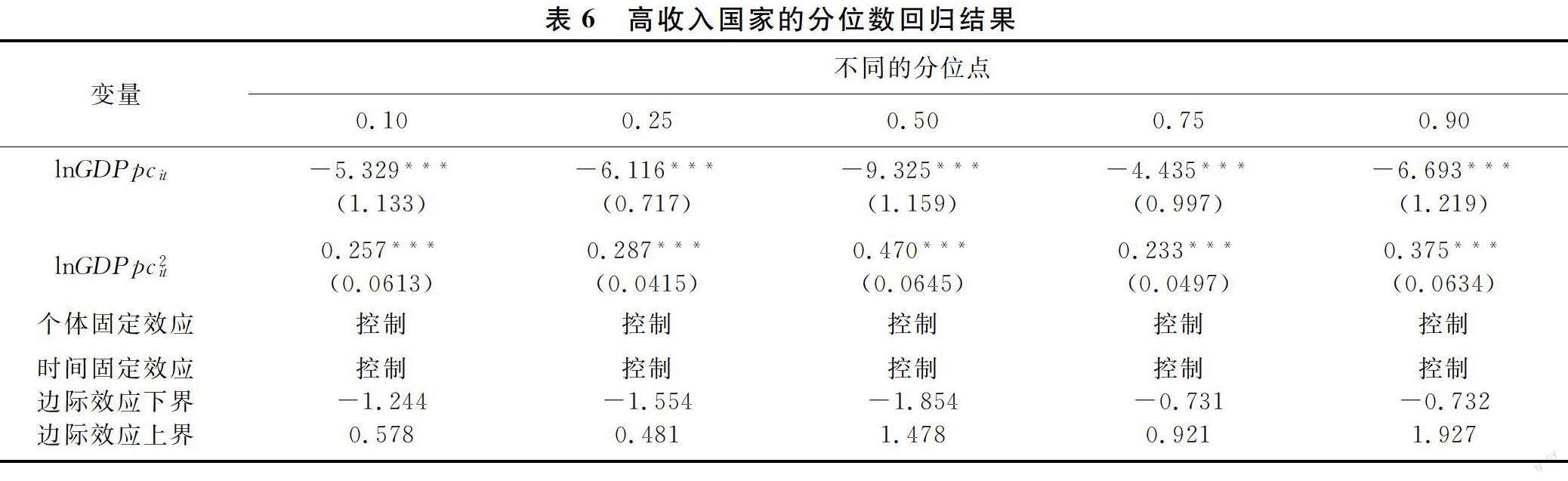
表6和表7分別给出了针对高收入国家和GDPpc-high这2个子样本的分位数回归结果。其中，0.10表示低分位数，0.25表示中低分位数，0.50表示中分位数，0.75表示中高分位数，0.90表示高分位数。除了给出分位数回归结果外，表6和表7还给出了边际效应的下界和上界。

表6和表7中分位数回归结果括号内的数字为采用MCMC方法得到的估计标准误。“*”“^**”和“^***”分别表示对应系数在0.1、0.05、0.01水平上显著。

由表6和表7可知，对高收入国家和GDPpc-high这2个子样本而言，在5个分位数处，边际效应的下界均为负值，这意味着，此时总和生育率与经济发展之间存在负相关关系。而边际效应的上界在5个分位数处的值都为正，这意味着，此时总和生育率与经济发展之间的负相关关系已经发生了逆转，转变为正相关关系，即总和生育率与经济发展之间存在反向“J”型关系，这与基准回归的结果是一致的。此外，lnGDPpcit和lnGDPpc2it 在5个分位点处的回归系数的估计值各不相同，这表明在不同的分位点处，总和生育率和经济发展之间的反向“J”型关系是不同的。

表6和表7中的0.10和0.25分别表示低生育水平的国家和较低生育水平的国家，而0.75和0.90分别表示较高生育水平的国家和高生育水平的国家。为了更准确地检验不同生育水平下的反向“J”型关系是否显著不同，表8给出了高收入国家和GDPpc-high这2个子样本的分位数回归系数显著性差异的Wald检验。

由表8易知，与生育水平相对较低的国家（0.10和0.25）相比，在生育水平较高的国家（0.90和0.75）中，经济发展对总和生育率的影响是显著不同的。也就是说，在不同的生育水平下，总和生育率和经济发展之间的反向“J”型关系是显著不同的。进一步可以看出，反向“J”型关系的负斜率和正斜率均随生育率的不同而不同。对正斜率而言，GDPpc的增加，将导致TFR增加的量随生育率的不同而不同。对负斜率而言，GDPpc的增加，将导致TFR减少的量随生育率的不同而不同。这表明，除了GDPpc外还有其他因素影响总和生育率，这些因素中可能包括家庭政策、女性就业等。

在高收入国家和GDPpc-high这2个子样本中，生育率与经济发展之间存在反向“J”型关系，这可能是因为在这些发达的国家（或地区），偏向技能的技术变革增加了技能溢价，从而降低了儿童保育服务的相对价格。也可能是因为这些发达的国家实施了鼓励生育的家庭政策，从而降低了父母生育孩子的机会成本。此外，在不同生育水平的国家，经济发展与总和生育率之间的反向“J”型关系是不同的。也就是说，生育率与经济发展之间的反向“J”型关系不仅取决于经济发展水平，也与生育率有关。这可能是因为不同的发达国家其生育率不同，实施的家庭政策也不尽相同等。

五 政策建议

自改革开放以来，我国经济取得了快速的发展，到2021年，人均GDP已接近世界平均水平。在经济快速发展的同时，我国的总和生育率却经历了大幅度下降。甚至有专家认为，我国已经掉入了“低生育率陷阱”。我国第七次人口普查的数据显示，我国的总和生育率已跌至1.3，已经低于国际上通常认为的 “高度敏感警戒线”。在世界范围内，总和生育率低于1.3的国家（或地区）仅有韩国，新加坡，中国的香港、澳门等少数几个国家（或地区）。基于前面的实证分析结果，就如何改变当前我国生育率极低的现状提出如下政策建议：

首先，实证分析结果表明，在高收入国家和GDPpc-high这2个子样本中，生育率与经济发展之间存在反向“J”型关系。而在低收入国家、中下收入国家、中上收入国家、GDPpc-low、GDPpc-middle这5个子样本中，没有观测到总和生育率与经济发展之间存在反向“J”型关系。也就是说，只有当经济发展到一定阶段后，总和生育率才有可能回升。所以，我国应该通过技术创新和产业升级等，寻求新的经济增长点，进而提高经济发展水平。

其次，建议借鉴国外的经验，并结合目前我国的国情，出台有助于提高我国生育率的家庭政策。例如，降低住房价格、养育孩子的成本、教育的费用等，进而缓解年轻人生育孩子的压力。

再次，需要意识到的是，虽然在高收入国家和GDPpc-high这2个子样本中，总和生育率与经济发展之间存在反向“J”型关系，但图1和图2进一步表明：对多数观测值而言，TFR和GDPpc之间存在负相关关系，仅有少部分观测值的TFR是随着GDPpc的增加而增加。另外，斜率为正的部分，拟合线倾斜程度较小。也就是说，虽然TFR随着GDPpc的增加而增加，但增加幅度较小。尽管很多发达国家为了逆转TFR，采取了不尽相同的政策，但TFR增加的幅度依旧不大。这意味着，对现阶段生育率极低的我国而言，只有最大限度地实施“鼓励生育”的政策，才有可能使我国的生育率缓慢回升。

［参 考 文 献］

［1］

Chen J， Retherford R D， Choe M K， et al. Effects of population policy and economic reform on the trend in fertility in Guangdong province， China， 1975–2005[J]. Population Studies， 2010（1）： 43-60.

［2］ Kitaura K， Yakita A. School education， learning by doing， and fertility in economic development[J]. Review of Development Economics， 2010（4）： 736-749.

［3］ Zakaria M， Fida B A， Janjua S Y， et al. Fertility and financial development in South Asia[J]. Social Indicators Research， 2017（2）： 645-668.

［4］ Madsen J B， Moslehi S， Wang C. What has driven the great fertility decline in developing countries since 1960？[J]. The Journal of Development Studies， 2018（4）： 738-757.

［5］ Gtmark F， Andersson M. Human fertility in relation to education， economy， religion， contraception， and family planning programs[J]. BMC Public Health， 2020（1）： 1-17

［6］ Furuoka F. Total fertility rate and per capita income： new empirical findings from France[J]. Actual Problems of Economics， 2012 （3）： 469-479.

［7］ Furuoka F. Is there a reversal in fertility decline？ An economic analysis of the “fertility J-curve”[J]. Transformations in Business and Economics， 2013（2）：44-57.

［8］ Brueckner M， Schwandt H. Income and population growth[J]. The Economic Journal， 2015（589）： 1653-1676.

［9］ Myrskyl? M， Kohler H P， Billari F C. Advances in development reverse fertility declines[J]. Nature， 2009（7256）：741-743.

［10］Dominiak P， Lechman E， Okonowicz A. Fertility rebound and economic growth： New evidence for 18 countries over the period 1970-2011[J]. Equilibrium-Quarterly Journal of Economics and Economic Policy， 2015（1）： 91-112.

［11］Luci-Greulich A， Thévenon O. Does economic advancement ‘cause a re-increase in fertility？ An empirical analysis for OECD countries （1960–2007）[J]. European Journal of Population， 2014（2）： 187-221.

［12］Ohinata A， Varvarigos D. Demographic transition and fertility rebound in economic development[J]. The Scandinavian Journal of Economics， 2020（4）： 1640-1670.

［13］Fox J， Klüsener S， Myrskyl? M. Is a positive relationship between fertility and economic development emerging at the sub-national regional level？ Theoretical considerations and evidence from Europe[J]. European Journal of Population， 2019（3）： 487-518.

［14］Becker G S， Barro R J. A reformulation of the economic theory of fertility[J]. The Quarterly Journal of Economics， 1988（1）： 1-25.

［15］Barro R J， Becker G S. Fertility choice in a model of economic growth[J]. Econometrica， 1989（2）： 481-501.

［16］Sprague A. Post-war fertility and female labour force participation rates[J]. The Economic Journal， 1988（392）：682-700.

［17］Becker G S， Lewis H G. On the interaction between the quantity and quality of children[J]. Journal of Political Economy， 1973（2）： 279-288.

［18］Day C. The dynamics of fertility and growth： Baby boom， bust and bounce-back[J]. The B.E. Journal of Macroeconomics， 2004（1）： 114-132.

［19］Martínez D F， Iza A. Skill premium effects on fertility and female labor force supply[J]. Journal of Population Economics， 2004（1）： 1-16.

［20］Begall K， Mills M. The impact of subjective work control， job strain and work–family conflict on fertility intentions： A European comparison[J]. European Journal of Population， 2011（4）： 433-456.