空射诱饵弹干扰资源动态分配策略
2023-05-31陈美杉刘赢曾维贵钱坤
陈美杉, 刘赢, 曾维贵, 钱坤
(海军航空大学, 山东 烟台 264001)
0 引言
微型空射诱饵(MALD)是美军的一款具备射频综合功能的电子战辅助突击武器,可执行集“侦干打”于一体的网络集群作战,近年来受到各国普遍重视[1-3]。目前,国内关于MALD的研究主要包括效能评估和挂载方案等[4-9],而对其协同干扰中资源分配策略研究较少,且研究中缺少对任务背景、装备特点和载荷功能的考虑与分析。
一个完整的干扰资源分配过程涉及雷达威胁评估、干扰效能评估、资源分配模型构建和求解等内容。
目标威胁评估是干扰资源分配的重要依据,现有资源分配研究中涉及威胁评估部分仅仅将其作为定值分析,没有考虑其随战场环境改变而动态变化的特点。
资源分配中涉及到的干扰效能评估往往是通过分析对抗过程寻求效能矩阵。目前效能矩阵确定方法可总结为两大类别:一是从干扰方出发,通过分析干扰参量的匹配程度和隶属程度研究干扰效能情况。文献[10-12]通过时、空、频、能和干扰样式等指标,结合模糊评价、博弈论等理论方法构建效能矩阵。二是从被干扰方的指标变化出发,反推干扰效能。文献[13-14]着眼干扰效果,选取雷达定位精度、发现概率等评估指标,通过干扰过程分析,构建效能矩阵。本文拟从匹配度入手,构建MALD干扰效能矩阵。但目前该方法的研究背景多是以噪声压制干扰为主,不完全适用于MALD储频转发有源多假目标干扰作战特点。因此,在具体理论研究中,需对效能评估模型适用性进行改进。
干扰资源分配模型构建方面,目前主要是基于威胁评估与效能评估构建符合科学实际的分配模型,并通过设置一定的约束条件,得到最终的寻优函数[11-17]。
在模型求解方面,传统方法包括模拟退火算法[18]、贴近度、0-1规划[19]等,虽然相对容易实现,但是仅适用于解决小规模分配问题。随着战场要素增多,启发式智能算法逐步占据主流,目前较常用的有遗传算法[20]、粒子群优化(PSO)算法[21]、蚁群算法(ACA)等,通过改进优化能较好地解决干扰资源分配问题。但在动态干扰资源分配时,较少有研究关注如何提高算法的时效性,仅是将动态对抗场景作为研究背景,实际上研究的仍然是单一时刻的资源分配问题。
针对上述研究现状,本文针对MALD干扰资源分配问题做出以下改进:1)引入变权理论计算目标动态威胁值,解决由于目标威胁值不变导致干扰资源分配不精确的问题;2)通过分析MALD载荷功能特点,将基于压制干扰时各因子的匹配度模型改进为假目标欺骗干扰模型,增强效能评估矩阵适用性与科学性;3)通过改进PSO算法,使其具备更快收敛速度。
1 系统配置
1.1 MALD有源干扰样式分析
MALD在对敌进行防空压制时,通常采用多弹协同抵近干扰战术策略,而关于其所使用的干扰样式和具体技术细节,官方并未披露。通过机理性分析可知,传统有源压制干扰在弥补接收端各类增益基础上仍需要有20 dB以上的冗余,而对于大型警戒雷达和相控阵雷达,实施有效压制的信干比要求达到60 dB以上。MALD这类小型干扰设备由于弹载空间和供电限制,功率无法做大,若考虑用距离弥补功率不足,则MALD又面临被强功率烧穿的风险,因此其通常不会采用传统的噪声压制干扰而是有源多假目标欺骗干扰。图1所示为MALD进行有源多假目标欺骗干扰原理示意图。

图1 空射有源诱饵原理结构示意图Fig.1 Schematic diagram of the principle and structure of MALD
经上述分析,初步判断MALD可利用数字无线电频率存储器(DRFM)技术,进行间歇采样转发式干扰,通过对雷达脉冲前沿进行复制并以小于脉冲宽度的时延转发出去,从雷达旁瓣进入,产生多假目标(群),兼具数量压制和欺骗干扰的双重效果。
1.2 系统配置及约束
假设有Q个目标执行突防组网雷达的任务,组网雷达系统由M部雷达组成,为提高突防概率,N发空射诱饵弹执行先期干扰任务。协同干扰建立在已知组网雷达基本参数的前提下(MALD具备战场侦察能力),如雷达位置、载频、脉宽、重频等。
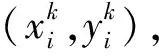

(1)
(2)
式(2)表示每发MALD不能同时干扰两部雷达。
为保证所有雷达均能被干扰,并且干扰资源被充分利用,设定分配给每部雷达的MALD个数不超过S,即
(3)

因此当多发MALD干扰组网雷达时,可以用三元变量来描述整个系统的干扰状态:
zk=f(Φk,Ek,Xk),k=1,2,…,T
(4)
(5)
式中:zk表示k时刻的综合干扰效能值;Z表示综合干扰效能值。动态干扰资源分配就是在满足约束条件的前提下,始终选择使干扰效能值最优的分配方案。
2 基于ICRITIC-变权理论的威胁评估
理论上,不同时刻各目标相对于MALD的威胁程度是一个动态变化的过程,本节基于变权理论求解各时刻不同雷达目标的动态威胁值。
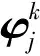
2.1 ICRITIC法确定初始权重
对于诱饵弹j,定义组网雷达的威胁指标分别为δu,u=1,2,…,4(分别为距离、载频、脉宽、重频4项指标),参照文献[23-24]的方法构建威胁评估矩阵并标准化得到X=[xiu]M×P,xiu表示第i部雷达的指标δu的标准化数值,P表示指标数目。
定义单个指标包含的信息量为
(6)

(7)
(8)
根据式(6)计算改进CRITIC方法后的指标常权向量ω=(ω1,ω2,…,ωu,…,ωP):
(9)
2.2 变权理论计算动态权重
相应的变权向量W(X)可以表示为
W(X)=[ω1(X),ω2(X),…,ωP(X)]=
W(x1,x2,…,xP)
(10)
变权方法[22]为构造状态变权向量实现对状态的加权调整,避免状态不均衡。状态变权向量可以表示为映射关系:
Sx:[0,1]p→[0,1]p,X→Sx(X)=Sx·X=[S1(X),S2(X),…,SP(X)]·(x1,x2,…,xP)=[S1(X)·x1,S2(X)·x2,…,SP(X)·xP]
(11)
变权向量W(X)可以通过状态变权向量Sx与常权向量ω的Hadamard乘积得到:
(12)
根据文献[25],由于本文威胁指标δu,u=1,2,…,4分别为距离、载频、脉宽和重频4项,干扰过程中距离的变化最为显著。假设其他3项指标不会有大幅度变动,本文采用混合型变权模型,分别构造均衡函数如下:
1)随着双方交战距离靠近,当MALD达到有效干扰作用距离后,距离指标对威胁程度的影响越来越小。因此用非线性函数对距离指标进行惩罚性变权,均衡函数表示为
Bu=x1+βulnx1,u=1
(13)
式中:βu为变权因子,βu>0为激励变权,βu<0为惩罚变权。
2)MALD在不断抵近雷达网的过程中,弹上计算机会实时处理接收的雷达数据,并作出策略调整,且越接近雷达,MALD越需做出更加快速和敏捷的策略调整以保证被掩护目标的安全。根据其工作原理可知,雷达脉宽影响对干扰延迟时间的把控,重频的变化又直接影响干扰脉冲串的使用策略。因此距离越近,脉宽和重频的细微变化对突防一方威胁程度的影响越大,用正相关非线性函数进行激励性变权,均衡函数表示为
(14)
3)由于MALD采用储频转发干扰体制,载频对于MALD而言,在其干扰的各个阶段重要性基本保持平稳,用1阶线性函数表示为
Bu=x1,u=2
(15)
基于此分析,综合均衡函数表示为
(16)
各指标的状态变权向量表示为
(17)
综上所述,各指标的变权重表示为
(18)
2.3 确定组网雷达威胁值
本节通过相对贴近度求解各目标威胁程度。传统相对贴近度[26]仅考虑目标参数之间的欧氏距离,不能直接反映各目标指标序列的态势变化情况,灰色关联度通过指标间整体趋势的相似程度在一定程度上体现了指标的相对重要性,因此本节引入灰色关联分析改进传统相对贴近度进行求解,具体步骤如下:
步骤1参照文献[22]确定威胁评估矩阵X=[xiu]M×P的正负理想解X+和X-。
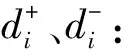
(19)
(20)
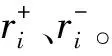
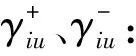
(21)
(22)
式中:ρ为分辨系数,ρ∈[0,1],一般取0.5。
其次对灰色关联系数加权求和,得到灰色关联度:
(23)
(24)
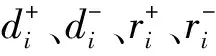
(25)
(26)

(27)
(28)
式中:α、β分别表示两种度量的权重,满足α+β=1。
步骤6根据相对贴近度求解各目标的威胁值:
(29)
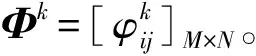
3 基于干扰指标的干扰匹配度分析
实现最佳干扰效能的关键是保证干扰的有效性。文献[15]中指出一般有效干扰需满足的时空频能等6项必要条件。MALD实施有源假目标干扰时在时间、空间、频率、能量和干扰样式的匹配度方面有其自身的独特性。
3.1 干扰时机
MALD干扰时机应满足下述要求:1)要对雷达脉冲前沿进行复制以掌握准确的干扰开始实施时机;2)有源多假目标一般要求信号转发的延迟时间要小于雷达脉冲宽度以达到较佳干扰效果,但这是非严格的;3)为保证足够的干扰能量和预期干扰效果,干扰要有一定的持续时间。另外,在一个脉冲间隔内的假目标数量应适中,假目标过少欺骗效果不佳,过多可能会被雷达处理端直接剔除,假目标数量的控制视情而定。下面对前3个时机影响因素的匹配度进行描述。
1)对于脉冲前沿采集时机匹配度,认为干扰机可以概率1检测到脉冲前沿:
et1ij=1
(30)
2)对于延迟时间匹配程度,若延迟时间Δt小于等于脉冲宽度ΔT,则匹配度取1;若延迟时间Δt大于脉冲宽度ΔT,则MALD会以一定概率实现假目标干扰:
(31)
3)对于干扰持续时间,采用占比率描述匹配程度:
(32)
式中:t1表示雷达威胁开始时刻;t2表示雷达威胁结束时刻;ti表示开始实施干扰时刻。
最终,干扰时机的匹配度表示为
etij=et1ij·et2ij·et3ij
(33)
3.2 干扰空间
干扰空间要素主要包括波束对准与覆盖范围、极化方式以及工作距离3个方面。
1)波束对准与覆盖范围。在量化描述波束问题时,需要明确空间“对准”的本质是保证足够的干扰能量进入到雷达接收机。因此将MALD方向上雷达增益的下降值作为方向上的对准程度:
(34)
式中:Gt表示被干扰雷达主瓣增益;ΔG′t表示诱饵弹工作方向上雷达增益值的损失量。
2)极化方式。保持干扰信号与雷达接收机极化方向一致是有效干扰的必要条件之一,为了总是能有信号进入雷达接收机,干扰机通常会选择圆极化方式,这样便存在一个损失系数,定义为epoij,取0.5。
3)工作距离。MALD在干扰过程中存在有效工作距离,与雷达相距过远时无法达到有效干扰距离,过近时一旦进入烧穿距离同样无法达到干扰目的。在有效作用距离范围内,MALD距离雷达越近,干扰效果越好,因此距离指标的匹配程度描述如下:
(35)
式中:Reff表示MALD有效作用距离;Rdis表示雷达与MALD之间的距离;Rbt表示烧穿距离。
3.3 干扰频率
对于MALD“侦察-转发-干扰”类型的“瞄频”模式而言,频率存在天然对准性,频率的匹配程度主要与雷达抗干扰体制相关。因此,给出适用于MALD的频率匹配模型如下:
(36)
3.4 干扰功率
通常用功率表征干扰设备的能量水平,而最终到达被干扰设备的功率大小与干扰样式、雷达体制和空间位置等多种因素有关。但无论选择何种方式,都要达到最基本的干信比需求,以保证干扰信号被检测到。这里,借用“压制系数”概念进行宏观效果描述,满足有效干扰的最小干扰功率计算公式为
(37)
式中:Pri为第i部雷达接收到的干扰信号功率;Prs为目标回波功率;Kj为第j发诱饵弹雷达正常工作所需最小干信比。
3.5 干扰样式
干扰设备采用的干扰样式必须要与雷达体制相匹配,且匹配程度越高,干扰效果越好。对于MALD而言,预存的波形产生方式和干扰样式决策库决定了其战场可用干扰样式的灵活性。这里选择有效干扰样式数量与MALD具备的干扰样式总数量的比值描述干扰样式带来的效能:
(38)
式中:Jeij表示第j发诱饵弹对第i部雷达的有效干扰样式;Jj表示第j发诱饵弹所具备的诱饵弹所具备的干扰样式总数量。
3.6 指标贡献度分析与权重确定
指标权重根据各项指标在干扰过程中的贡献程度大小给出。根据MALD在上述指定背景下的作战特点,同时结合专家经验,认为MALD在进行有源假目标转发干扰时,在干扰时机、干扰作用距离和干扰样式三方面对干扰效果的影响较大,其余3项指标影响相对较弱。现给出除极化方式匹配指标外,其余6项指标(干扰时间、波束对准程度、干扰距离、干扰频率、干扰功率、干扰样式)的权重值:
WJ=[ωtωbωrωfωpωs]=[0.3 0.1 0.2 0.1 0.1 0.2]
(39)
3.7 构建综合干扰效能矩阵
干扰效能的产生是各指标共同作用的结果,一旦其中一个指标失效,则干扰失效。因此使用扎德算子取小计算,即
a∧b=min (a,b)
(40)
式中:a、b分别表示各项指标。由此得到干扰效能模型为
(41)
式中:E=[etij,ebij,erij,efij,epij,esij]。进而得到效益矩阵E=[eij]M×N。
4 综合干扰资源分配优化算法
4.1 干扰资源优化分配模型
根据第3节对动态威胁评估和干扰效能匹配度矩阵生成的研究,给出最终资源分配方案生成思路框架如图3所示。

图3 干扰资源分配方案生成框架Fig.3 Frame diagram of jamming resource allocation scheme generation
当干扰资源有限时,资源的不合理配置会造成资源利用率低,甚至会造成干扰效果不理想。本文所提的面向组网雷达的分配思路为在干扰资源有限的条件下,通过整合目标威胁值和干扰匹配度矩阵,最大化MALD对组网雷达的干扰效能,其优化模型可建立为
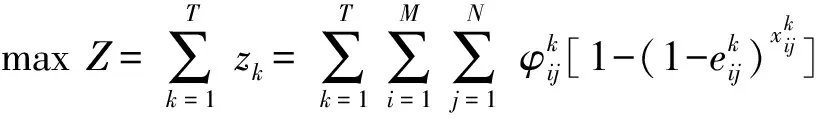
(42)

从式(42)中可以看出,本文实际建立了一个带干扰资源约束条件的数学优化问题。约束1表示每部雷达均能被干扰,且最多受到S发MALD的干扰;约束2和约束3表示每发MALD同一时刻只能干扰一部雷达。
4.2 改进PSO算法求解
4.2.1 PSO算法
设搜索空间为n维,粒子p,p∈[1,M](M为种群规模)的当前位置Xp、当前速度vp及个体最优位置Pbp分别为Xp=(Xp1,Xp2,…,Xpn),vp=(vp1,vp2,…,vpn),Pbp=(Pbp1,Pbp2,…,Pbpn)。
对于最大化目标函数,粒子p的个体最优位置的计算公式如下:
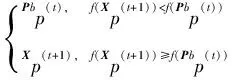
(43)
式中:f(·)为目标函数;t为迭代次数。
每次迭代后,群体中所有粒子经历过的最好位置称为全局最优Pg(t),即
f(Pg(t))=max {f(Pb1(t)),f(Pb2(t)),…,f(PbM(t))}Pg(t)∈{Pb1(t),Pb2(t),…,PbM(t)}
(44)
则基本PSO算法的更新方程如下:
vpq(t+1)=ω(t)vpq(t)+c1r1q(t)(Pbpq(t)-Xpq(t))+c2r2q(t)(Pgq(t)-Xpq(t))
(45)
Xpq(t+1)=Xpq(t)+vpq(t+1)
(46)
式中:ω(t)为惯性权重;vpq(t)为粒子p第q维第t次迭代的速度;c1、c2为学习因子;Pbpq(t)为粒子p第q维第t次迭代所经历的最好位置;Xpq(t)为粒子p第q维第t次迭代的当前位置;r1q(t)、r2q(t)分别为[0,1]内的随机数;Pgq(t)为第q维第t次迭代的全局最好位置。
4.2.2 改进PSO算法
改进PSO算法主要体现在以下3个方面:
1)不同于其他优化问题,MALD干扰资源分配求解的是各诱饵弹干扰的雷达目标编号,因此需要对粒子采用整数编码的方式[27]。
2)标准PSO算法多采用如式(47)所示的线性惯性权重:
ω(t)=(tmax-t)(ωmax-ωmin)/tmax+ωmin
(47)
式中:ωmax、ωmin分别为惯性权重的最大值和最小值,一般取1.0和0.3;tmax为最大迭代次数。
其特性为初期惯性权重大,有利于进行全局搜索;后期惯性权重小,有利于局部寻优,但容易导致粒子过快聚集,多样性消失,导致不能收敛到全局最优解,自适应惯性权重策略可针对性改善其性能。由于目标函数为非线性函数,本文选用自适应惯性权重[28]对PSO算法进行改进。
3)在动态优化问题中,由于综合干扰效能只与当前和未来干扰效能相关,而与过去的信息无关,因此干扰分配策略的确定符合马尔可夫决策过程。文献[29]提到,对于动态优化问题,能够通过在后续分配中继承初次分配的结果提高寻优效率,而PSO算法需要由相同的初始状态开始寻优,相比继承前一时刻的最优方案,PSO算法需要探索更多的动作,耗时较长,效率较低。本节借鉴文献[29]的思想,在动态求解时通过继承前一时刻的最优方案对种群进行初始化。
实际上,在动态优化问题中,无论是连续解空间还是离散解空间,最优方案在时间这一维度上都具有连续性,即相邻两时刻的最优方案在解空间中是相邻的,因此本节通过继承前一时刻的最优方案,同时结合自适应惯性权重,能够在最大限度提高寻优效率的同时,避免陷入局部最优。
算法具体步骤如下:
步骤1随机初始化种群中各微粒的位置和速度。如微粒x=[3,4,1,6,5,2]位置表示诱饵弹3干扰雷达1,诱饵弹4干扰雷达2,诱饵弹1干扰雷达3,……以此类推。
步骤2计算各微粒的适应度。将当前粒子的位置和适应度存储于各微粒的个体最优Pbp(t)中,将全部个体最优中适应度最优的粒子位置和适应度存储于全局最优Pg(t)中。
步骤3根据式(45)、式(46)更新粒子的速度与位置。
步骤4自适应更新惯性权重
ω(t)=(ωmax-ωmin)Ps(t)+ωmin
(48)
式中:ωmax、ωmin一般取0.9,0.3;Ps(t)为移动到更优处粒子的占比,具体定义如下:
(49)
(50)
步骤5若达到一定的精度要求(通常为预设的精度阈值或迭代次数),则输出结果;否则返回步骤3继续搜索。
步骤6在后续各时刻中,将上一时刻的最优分配结果所对应的微粒随机继承给初始化种群中的任一粒子。
通过步骤6,使得PSO算法能够迅速聚集到上一时刻的最优粒子附近,同时自适应惯性权重也保证了合适的搜索范围,避免收敛到局部最优,因此在一定程度上提高了搜索效率。
但由于本文PSO算法的解空间是离散的,不同于连续性的解空间,容易产生一段时间内最优方案始终不变的情况。改进PSO算法的流程如图4所示。

图4 改进PSO算法流程图Fig.4 IPSO algorithm flowchart
5 仿真结果与分析
本节通过仿真实验求解资源分配方案,并将改进PSO算法与传统算法进行比较,验证本文所提与算法的有效性。
5.1 仿真参数设置与说明
考虑作战场景中组网雷达系统由6部雷达组成,突防系统为8发MALD掩护目标,MALD实施抵近干扰以保护目标突防。组网雷达与MALD的参数设置分别如表1和表2所示。选取30 s突防数据进行算例分析,数据间隔为1 s,共30组数据。
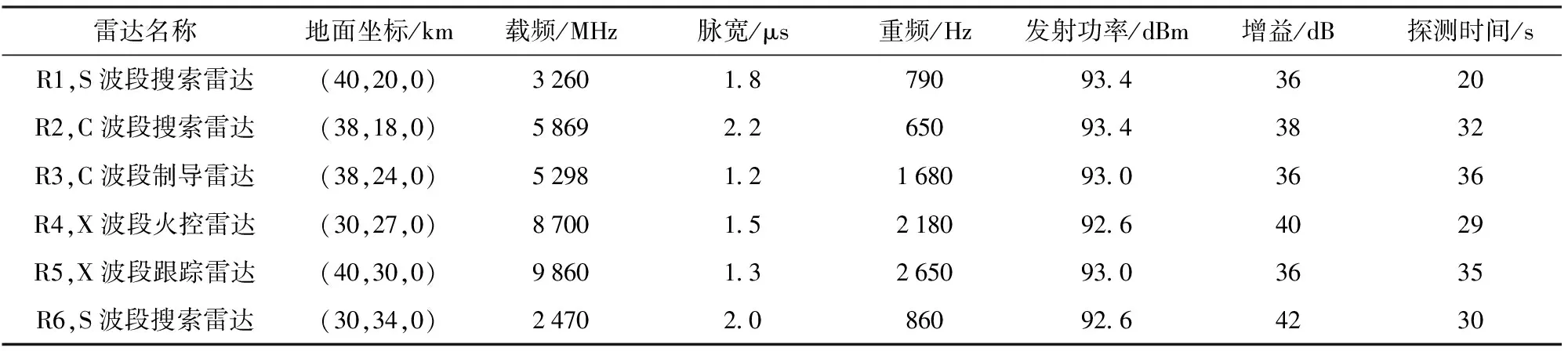
表1 初始时刻雷达仿真参数
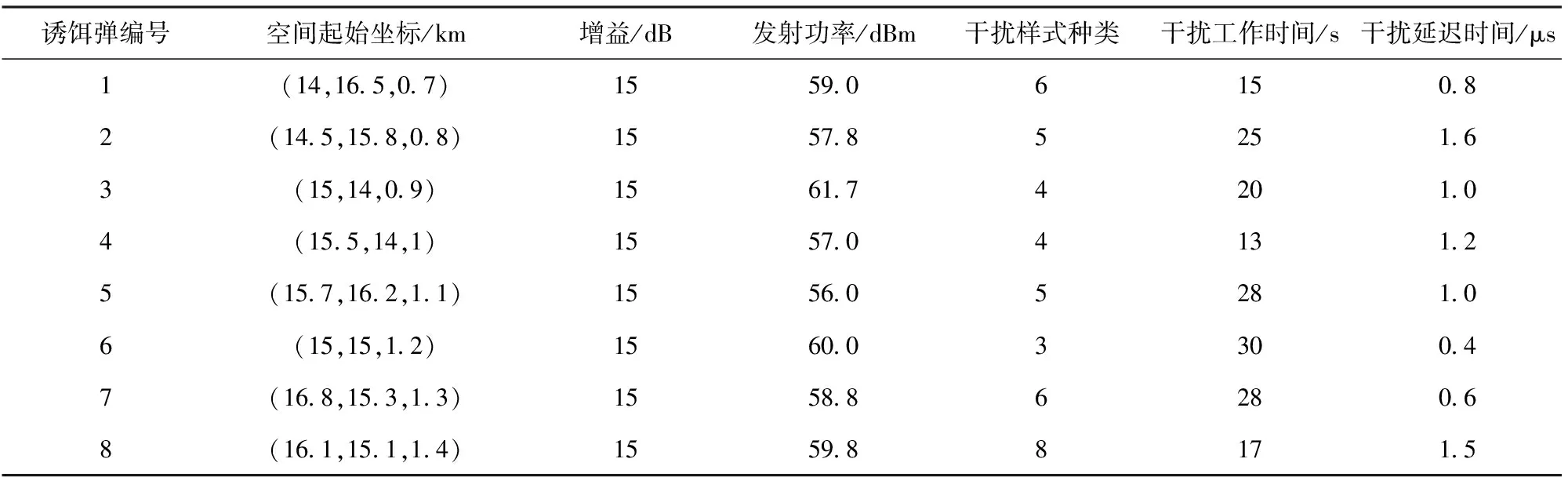
表2 初始时刻诱饵弹仿真参数
组网雷达参数设置中,给出6部雷达初始载频、脉宽和重频参数。载频方面,设定雷达1、3、5、6为具备频率捷变抗干扰功能体制雷达,30 s内分别取相应频段内的若干频点进行跳变,雷达2、4不具备该功能,载频保持不变;脉宽和重频方面,给出6部雷达初始脉宽与重频,30 s内各参数随时间呈线性变化趋势。
MALD参数设置中,由于MALD一般采用0.7~0.8 Ma的飞行速度,30 s仿真时间内,MALD飞行距离大概在7~8 km,通过预置航路点方式规划MALD大致飞行航线,结合雷达空间坐标,得到目标突防组网雷达的空间位置关系如图5所示。图5中,R1、R2、R3、R4、R5、R6分别表示表1中对应的6部雷达。

图5 目标突防组网雷达系统空间关系图Fig.5 Scenario of target penetrating the NRS
5.2 实验过程
改进PSO算法参数设置如下:最大迭代次数为150;粒子群规模为50,ωmax取0.9,ωmin取0.3,Monte Carlo仿真次数为200。仿真平台均为Intel(R) Core(TM) i5-8250U CPU 3.40 GHz,MATLAB R2015b,在Windows 10操作系统下进行。
以其中1发MALD为例,对干扰资源优化分配步骤进行如下描述。
步骤1指标变权重求解。根据改进的CRITIC法,以该发MALD视角下的雷达6为例,确定其指标初始权重为ω=(0.329,0.220,0.258,0.194),通过对指标建立均衡函数,结合变权理论确定各指标权重的变化曲线如图6所示。

图6 雷达指标权重变化曲线Fig.6 Curves of radar index weight change
由图6可知,随着距离的变化,距离权重逐渐减小,脉宽、重频权重逐渐增大,载频权重趋于稳定,仿真结果与理论分析情况基本吻合,说明该变权方法与本文所研究内容具有较好适用性,其结果可用于后续分析。
步骤2组网雷达威胁值求解。分别计算该发MALD视角下组网雷达中各雷达的指标动态权重。通过各时刻下的指标变权重,结合改进相对贴近度的方法计算各时刻下组网雷达的威胁值,仿真结果如图7所示。

图7 各雷达威胁值变化曲线Fig.7 Curves of the threat value of each radar
由图7可知,随着时间推进和工作参数的变化,雷达的威胁值发生动态变化:0~13 s时刻,雷达威胁排序由高至低为[5,3,4,1,2,6];14~17 s时刻,雷达威胁排序由高至低为[5,4,3,1,2,6];18~30 s时刻,雷达威胁排序由高至低为[5,4,3,2,1,6]。从总体威胁等级看,雷达3、4、5为制导、火控和跟踪雷达,相较雷达1、2、6执行的警戒和搜索任务,对MALD的威胁程度始终较高。
步骤3优化算法动态资源分配方案。重复步骤1、步骤2,得到每发MALD视角下组网雷达的动态威胁值,根据本文的改进PSO算法对最优分配方案进行求解,表3为优化算法的资源分配结果,其中数字表示对应的雷达编号。
由表3可知,MALD群在干扰过程中的干扰策略大致分为3个阶段,即1~16 s时刻、17~22 s时刻和23~30 s时刻,由MALD分配数量可以看出:干扰资源始终保持对最高威胁等级的雷达5采用2发MALD进行持续干扰,过程中干扰资源由雷达3向雷达4侧重,原因在于雷达4的威胁程度不断增大,分配结果与图7结论基本吻合。
5.3 实验结果与对比分析
5.3.1 动态与传统干扰效能值对比分析
分别计算各时刻的最优干扰效能值,并与传统方法计算结果对比。传统算法通过2.1节的威胁评估方法确定固定权重,通过本文改进相对贴近度计算威胁值,最后采用传统PSO算法进行资源优化分配,实验结果如图8所示。

图8 最优干扰效能变化曲线Fig.8 Curves of optimal jamming effectiveness change
由于不涉及动态调整威胁值和资源分配,传统算法实际上仅对初始时刻的战场仿真数据进行资源分配,由此得到与本文动态分配方法初始时刻同样的效能值。
由图8可知,传统方法得到的效能值始终为1.331 3,而本文算法中随着时间的推移,MALD弹群的最优干扰效能值总体上呈上升趋势,最终达到1.559 1,显著高于传统方法得到的效能值。分析原因可知,一方面,传统分配方案为单一时刻的固定分配方案,新的分配方案是随干扰方参数、被干扰方参数和空间位置实时变化的动态分配方案;另一方面,由于改进PSO算法是不断优化迭代的,随着时间的推移,MALD执行干扰时的匹配度不断增强,干扰效能不断提高。
另外,动态效能值在17 s和23 s时刻左右出现明显下降拐点,随后效能值又稳步提升。由此可见,当干扰效能值出现下降时,改进后的算法可以迅速实现动态分配方案调整,保证最佳干扰效果。对于曲线中出现的拐点,分析是由于雷达威胁程度发生变化或是MALD抵近过程中被烧穿失效产生。
很显然,动态的干扰效能值更符合实际作战情况,MALD可根据战场态势实时调整干扰资源分配策略,始终保持最佳干扰效能。由此得到的干扰分配策略也更加具有针对性,在一定程度上提高了干扰资源的利用效率。
5.3.2 改进PSO与传统PSO算法、ACA性能对比
本节将改进PSO算法分别与传统PSO算法和ACA进行对比。其中,PSO算法的迭代次数、粒子群规模、Monte Carlo仿真次数与本文改进算法保持一致;ACA的蚂蚁个数为50,信息素重要程度参数为1,启发式因子重要程度参数为5,信息蒸发系数为0.01,最大迭代次数为150,信息素增加强度系数为100。分别从耗时性能、实时性和最优解正确率3个方面衡量本文算法性能。仿真结果如下。
1)算法耗时性与实时性对比分析
在MALD飞行过程中,每间隔0.5 s,采用不同算法进行干扰资源分配,选取若干时刻下3种方法的耗时与指标结果如表4所示。

表4 算法耗时性能对比
由表4可知:3种算法均可实现干扰资源分配,最终的干扰效能值也完全相同;不同方法在计算耗时上存在一定差异,初次分配时改进PSO算法耗时较长,而后续分配过程中PSO算法与ACA耗时较长。对于初次分配,改进PSO算法迭代过程中初始化参数更多,并探索更多的动作,因此耗时较长。在后续分配过程中,由于初始化种群中包含上一时刻的最优分配方案的粒子,改进PSO算法能够继承初次分配的结果,而PSO算法与ACA都需要由相同的初始状态出发进行寻优,因此改进PSO算法耗时更短,效率更高。
2)算法最优解正确率对比分析
分别计算3种算法200次Monte Carlo仿真中寻到最优解的仿真曲线平均值(15 s时刻),得到仿真平均曲线如图9所示;同时以1 000次Monte Carlo仿真为一轮实验,重复10轮,得到各算法的最优解正确率,并通过箱线图进行统计分析,对比结果如图10所示。
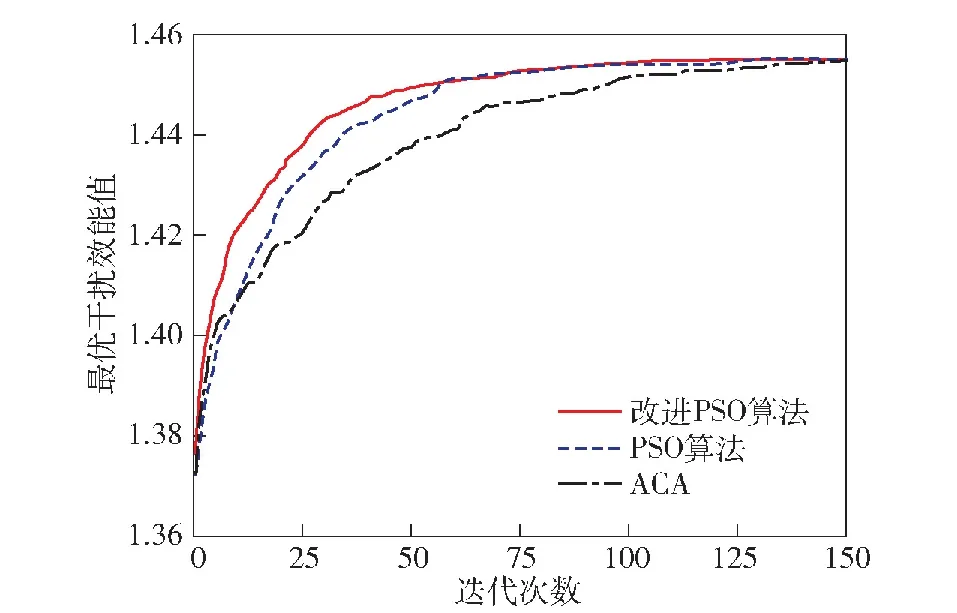
图9 算法迭代曲线对比Fig.9 Comparison of algorithm iteration curves

图10 最优解正确率对比分析Fig.10 Comparison of accuracy of optimal solution
分析图9可知,相较于传统PSO算法和ACA,本文的改进PSO算法能够以更快的收敛速度得到最优解;同时,分析图10可知,在同样的迭代次数下,本文改进算法可以达到的最优解正确率水平为95.6%,要优于传统PSO算法的93.2%和ACA的93.9%,且没有奇异值,因此具有更好的寻优稳定性。
分析可知,主要原因在于采用自适应惯性权重和变化学习因子后,改进PSO算法更易收敛、不易陷入局部最优解,在处理复杂函数问题过程中具有更强适应性,更适合干扰资源分配的优化问题。
6 结论
本文针对动态干扰资源分配中的一系列问题,提出了一种面向组网雷达的空射诱饵弹干扰资源动态分配方法。充分考虑MALD有源假目标干扰作战特点,通过引入匹配度概念,结合动态威胁评估方法,以最大化干扰效能为目标,构造了资源分配优化函数,之后采用改进PSO算法对上述优化问题进行求解。得出主要结论如下:
1)基于ICRITIC和变权理论的动态威胁评估方法可以得到敌方雷达威胁值的动态变化过程,使得最终的干扰分配策略更为合理,战场适用性更强。
2)充分考虑MALD干扰机理,引入并改进匹配度模型用于分析影响干扰效能的相关指标,得到的干扰效能值用于指导干扰资源分配,使得分配结果更加科学合理。
3) 改进PSO算法使得计算效率在非初次决策中相比传统算法在实时性和准确性方面具有更明显的优势。
