基于强化学习的对空雷达抗干扰波形设计

郑泽新, 李伟, 邹鲲, 李艳福

(空军工程大学 信息与导航学院, 陕西 西安 710077)

0 引言

现代战场中,电子战手段的发展严重影响着雷达性能,如被探测目标发展出箔条干扰和拖曳式干扰等无源干扰、压制干扰和欺骗干扰等有源干扰技术进行自我保护。这些手段可通过淹没或模糊目标回波、制造假目标等方式降低雷达对目标的检测和识别概率。尤其当敌方对雷达实施自卫干扰时,干扰信号从天线方向图主瓣进入接收机,导致通过波束置零抑制旁瓣干扰的空域抗干扰方法难以发挥效能,给对空雷达完成目标搜索、定位、跟踪、识别和成像等任务带来巨大挑战。

在雷达抗主瓣干扰方面,国内外学者已有研究,其中,波形捷变因抗干扰性能好而备受重视。目前从波形捷变角度抗干扰的方式主要有频率捷变和相位编码信号捷变。方文等[1]提出了,基于捷变频联合波形熵的密集假目标干扰抑制算法,全英汇等[2]对频率捷变雷达波形对抗技术发展趋势进行了展望。晏艺翡等[3]提出了一种基于干扰环境感知和低截获波形调度的抗主瓣干扰雷达设计方法。但是,脉间频率捷变雷达在相干处理时间内对跳频信号的处理会产生旁瓣,导致多普勒谱出现尖峰,而这些尖峰会被误认为是目标,导致虚警概率提高[4]。当相位编码信号用于波形捷变时,可带来很高的自相关函数主旁瓣比,也可形成很窄的自相关主瓣,拥有较高的互正交性能,进而带来较好的抗干扰性能。夏栋等[5]提出了利用相位编码变波形联合恒虚警技术抗同频干扰的方法,从同频干扰中提取出有用的目标回波信号,并且对强同频干扰具有较好的适应性。Hu等[6]提出了一种相位编码信号系统,有效抑制了主瓣干扰,提高了目标检测概率。Wang等[7]利用相位和频率编码波形技术,提出了一种抗重传干扰技术。但是,产生数目足够且相互正交的编码信号有很大困难,随着编码信号数目的增加,信号集内信号间互正交性能逐渐下降,导致转发式干扰和重构式干扰等干扰手段[8]基于前一个或前几个脉冲产生干扰信号时仍然能够获得一定的干扰性能。

现有波形捷变技术可对抗传统干扰,但无法应对具有预测能力的干扰机。若能从博弈角度预测干扰信号,设计雷达波形,则可进一步提升雷达的可靠性。基于博弈思想研究雷达和干扰间动态对抗已有一些成果。He等[9]针对多基地雷达网和智能干扰机博弈问题,提出了一种功率分配和波束形成的博弈算法。Ye等[10]提出了一种基于最小损失准则的抗干扰策略选择识别方法,基于博弈论将利润矩阵转化为最小损失决策矩阵,获得了最佳策略。Chen等[11]通过建立合作博弈模型,研究分布式多输入多输出(MIMO)雷达功率分配,验证了均匀功率分配通常不是最优。Shi等[12]研究了在多基地雷达系统中采用Stackelberg博弈方法的协作低截获概率性能优化问题。Wang等[13]通过合作博弈论的框架,在最小化雷达时间资源成本的同时形成了稳定的网络结构。基于纳什均衡[14]、Stackelberg模型[15]和Bayesian博弈模型[16]设计雷达波形,有效提高了雷达检测性能。但实际对抗场景中,参与博弈的因素众多,传统博弈模型需要人工进行博弈模型选择、参数更新和策略选择等工作,对操作人员的运算能力和知识水平提出了过高要求,无法摆脱模型的条件约束,难以得到真正的最优博弈策略。

强化学习具有强信息感知和交互能力,为博弈问题研究提供了一种全新的解决思路。现已有强化学习应用于雷达抗干扰的成果。Xing等[17]研究了基于强化学习的智能雷达对抗方法,提高了雷达对抗系统的适应性;并针对工作模式数量未知的情况,研究了基于强化学习的智能雷达对抗方法[18]。Selvi等[19]针对雷达通信共存问题,将雷达环境建模为马尔可夫决策过程,预测并使用最小化干扰频段。Li等[20]基于强化学习思想对认知雷达抗干扰跳频策略展开研究,利用深度Q网络等方法躲避干扰,并将深度强化学习思想用于雷达对抗主瓣干扰,获得了较高的检测概率[21]。Wang等[22]提出了基于强化学习的同址MIMO雷达认知波束形成算法。Cao等[23]关联波形参数选择与目标状态估计,建立了强化学习模型,实现了性能更优的波形选择算法。Wang等[24]提出了一种基于深度强化学习的认知雷达波形优化方法,提高了目标跟踪精度。Ak等[25]基于部分可观测马尔可夫决策过程模型,使用深度Q网络和长短时记忆网络生成两种跳频策略,提高了认知雷达抗干扰性能。Shi等[26]针对多机动目标跟踪中的雷达功率分配问题,提出了一种基于控制框架的深度确定性策略梯度认知设计。Ailiya等[27]提出了一种基于强化学习的联合自适应跳频和脉宽分配方案,利用Q-学习在环境信息不完备条件下生成了最优策略。

因此,本文将认知雷达和博弈思想结合,基于马尔可夫决策过程实现博弈场景建模,在干扰条件下,得到雷达信号的频域能量分配策略,合成时域最优雷达波形,并与传统信号进行性能对比。

1 信号模型与强化学习模型

1.1 信号模型

复杂电磁环境中,建立雷达和目标的博弈模型需要考虑雷达发射信号、目标回波、干扰、环境噪声和各类杂波等因素,如图1所示。图2为信号模型。假设雷达发射信号为s(t)、接收信号为y(t),信号带宽和功率为W与Ps;目标脉冲响应h(t)为时间Th有限的随机模型,r(t)为接收滤波器脉冲响应,H(f)与R(f)分别为h(t)与r(t)的傅里叶变换;不考虑杂波时,噪声n(t)为零均值高斯信道过程,其功率谱密度为Snn(f),W内不为零;每个脉冲发射前截获的主瓣压制干扰信号为j(t),总功率为PJ,功率谱密度为J(f)。

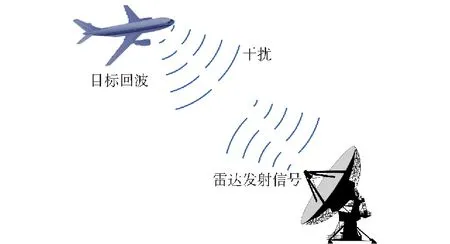
图1 雷达探测场景Fig.1 Radar detection scene

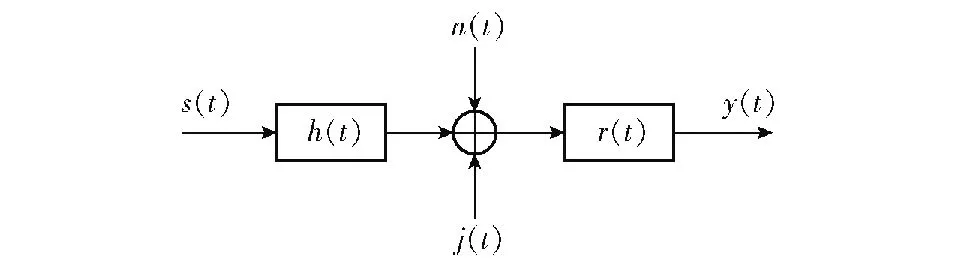
图2 信号模型Fig.2 Signal model

由图2可知,雷达接收端滤波器输出端信号[14]y(t)达式为

y(t)=r(t)*(s(t)*h(t)+n(t)+j(t))

(1)

式中:*为卷积运算符。雷达信号分量ys(t)、干扰和噪声分量yj(t)分别为

ys(t)=r(t)*(s(t)*h(t))

(2)

yj(t)=r(t)*(n(t)+j(t))

(3)

在t0时刻信号和干扰噪声比(SINR)的频域表达式为

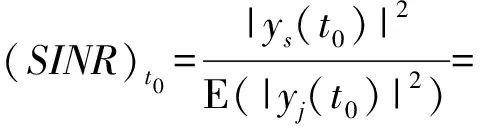
(4)

式中:S(f)为雷达发射信号s(f)的功率谱密度;E(·)为数学期望。

由文献[28]可知,假设目标脉冲响应为时间有限随机模型时,可用能量谱方差替代功率谱密度,即

(5)

式中:μh(f)为H(f)的均值。

设μh(f)=0,将式(5)代入式(4)中,利用施瓦茨不等式求解,可得

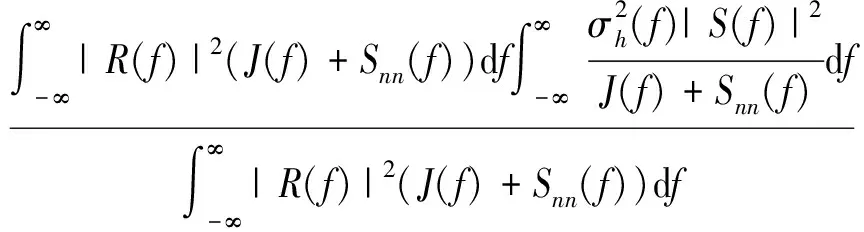
(6)

(7)

式中:Δf为频率采样间隔;K为频率采样数;W=KΔf;fk为频率采样点。

本文雷达检测问题与文献[15]相同,可定义为假设检验问题,通过经典Neyman-Pearson定理[29]求解,得雷达对目标检测概率PD为

(8)

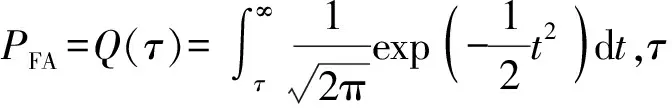
1.2 马尔可夫决策过程模型

马尔可夫决策过程具备马尔可夫性,即未来状态与过去状态无关,仅依赖当前状态和动作,公式表示为

P(st+1|st,at,st-1,at-1,…)=P(st+1|st,at)

(9)

式中:P(st+1|st,at)表示在状态st下采取动作at转移到状态st+1的概率。

因此,可将雷达和干扰间的动态对抗过程描述为马尔可夫决策过程模型。马尔可夫决策过程可定义为包含状态、行为、转移概率、奖励和折扣因子的五元组{S,A,P,R,γ}。状态集S定义为{干扰信号j(t)、噪声n(t)和目标冲激响应}组成的集合,其中状态s∈S是环境信息的唯一表征。将所有可能应对干扰信号的雷达发射信号s(t)组成动作集A。状态转移概率函数P(s,a,s′)是雷达针对不同干扰的状态s转换到干扰状态s′所采取的雷达信号a的概率,在没有先验知识且状态转移概率未知时,设初始状态转移概率均相等。奖励函数R(s,a,s′)是博弈方在状态s下执行动作a变换为状态s′的累计奖励平均值,根据博弈方所执行动作的好坏做出反馈。为了更好地确保状态序列是有限的,模型中设置折扣因子决定决策依赖于短期收益还是长期收益。折扣因子γ∈[0,1],当γ趋于0时,博弈方倾向于获得即时奖励;当γ趋于1时,博弈方更倾向于获得长期收益。

2 基于马尔可夫决策过程的波形设计方法

雷达在博弈过程中的波形变化过程具有马尔可夫性,利用强化学习方法对系统环境进行马尔可夫决策过程建模,可实现雷达和目标间的自适应波形博弈。马尔可夫决策模型设计雷达波形示意如图3所示,其中波形状态为S,当前状态的奖励为R,i∈{1,2,3,…},箭头上数字为状态转移概率。

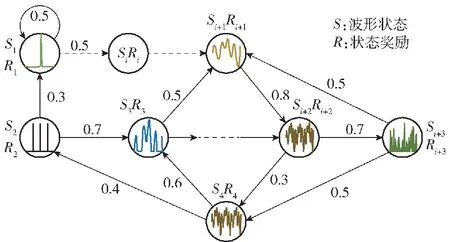
图3 马尔可夫决策过程示意图Fig.3 Schematic diagram of Markovdecision process

2.1 博弈环境建模

公式描述如下:

状态空间S定义为

S={s1,s2,…,sNM}

(10)

式中:下标NM表示状态集S的元素个数。令αi∈{0,1,…,N}表示第i个子频带上的功率分配情况,i∈{1,2,…,M},则单个状态表示为

si=(α1,α2,…,αM)

(11)

动作空间A定义为

A={a1,a2,…,aN′M′}

(12)

式中:下标N′M′表示动作集A的元素个数。令βi∈{0,1,…,N′}表示第i个子频带上的功率分配情况,i∈{1,2,…,M′},则单个动作表示为

ai=(β1,β2,…,βM′)

(13)

2.2 关键参数设置

强化学习模型的关键参数设置如表1所示。

表1 强化学习模型参数设置

奖励结构是影响智能体选择策略的重要因素,奖励结构的设置不同,智能体的决策倾向性就不同。雷达接收机的SINR与雷达探测性能密切相关,因此本文将SINR设置为奖励函数,如表2所示。

表2 奖励函数结构

2.3 最优策略生成

本文算法目标是利用马尔可夫决策过程对博弈环境建模,采用策略迭代法寻找雷达抗干扰的最优策略。策略π可理解为在某一状态s下选择某一动作a的概率,即

π(a|s)=P[At=a|St=s]

(14)

如果策略π确定,即可确定雷达在每种干扰状态下选择每个动作的概率。为评价策略π的回报值,定义累计回报G,表征从某一状态出发可能产生的若干条马尔可夫链的累计回报,表示为

(15)

对每一策略π中的状态s而言,可产生无数条马尔可夫链,为了评价某一个状态的回报价值,定义状态值函数v(s)为状态s的累计回报的期望,即

(16)

同理,定义状态-行为值函数q(s,a):

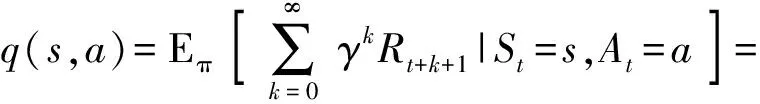
(17)

迭代策略分策略评估和策略改进两个步骤。先策略评估,在给定策略π下不断迭代求解,直至值函数收敛,公式如下:

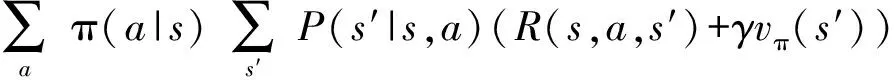
(18)

再通过在当前策略基础上贪婪选择能增加下一状态值的动作,以此更新策略π,改进后的策略π′为

(19)

更新的状态值为

(20)

由此即可得出最优策略[30]。

3 仿真结果与分析

实验仿真中,参数设置依据国外某型雷达,如表3所示。

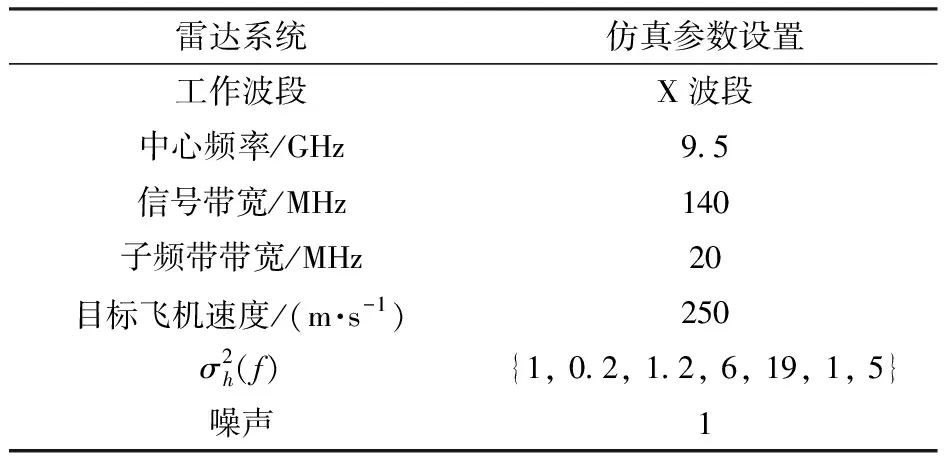
表3 仿真参数

3.1 雷达和干扰博弈过程

雷达和干扰作为博弈方,与环境信息交互,产生最优频域波形策略,博弈过程如图4、图5所示。

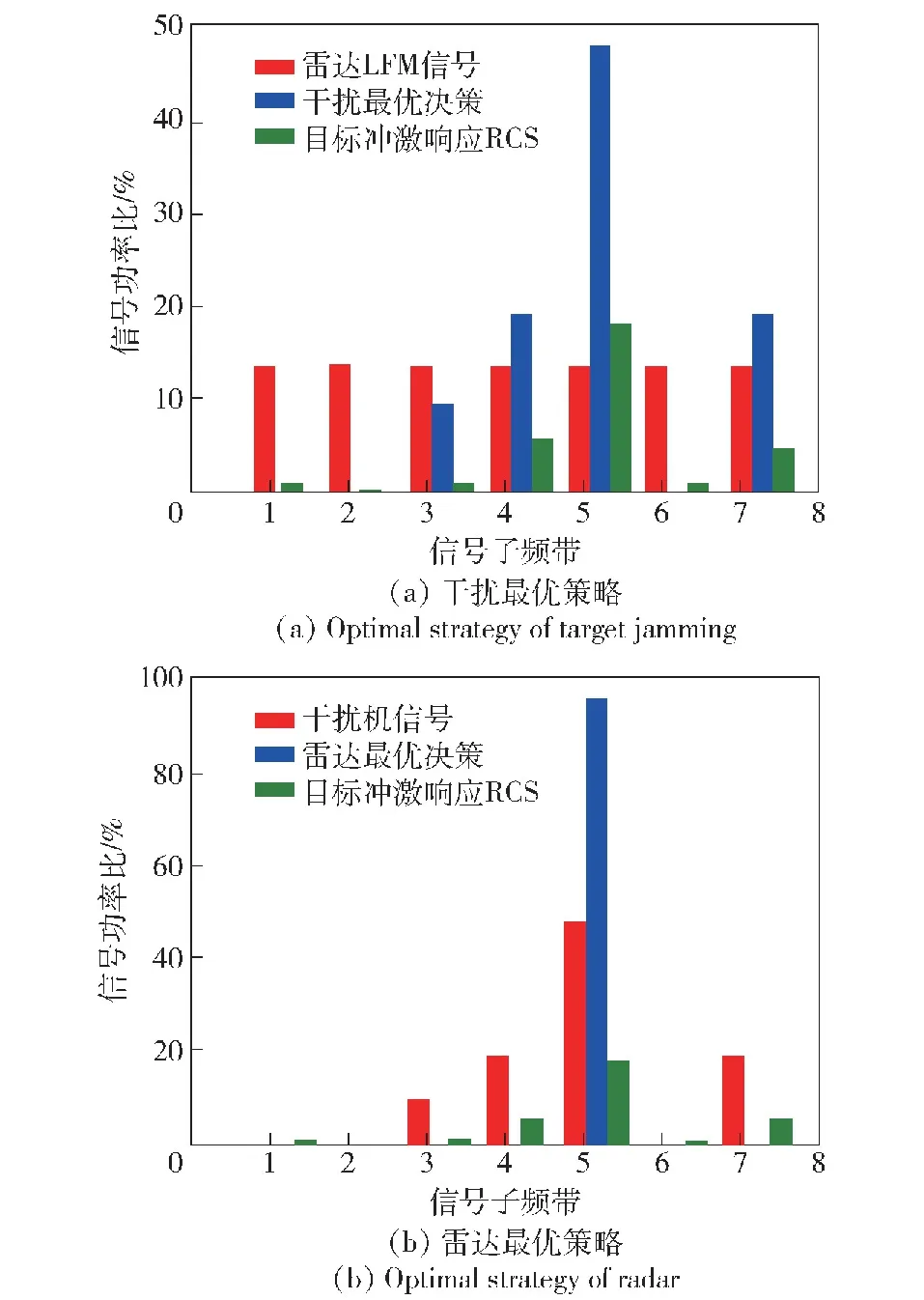
图4 雷达和干扰博弈过程一Fig.4 Game process one of radar and jamming

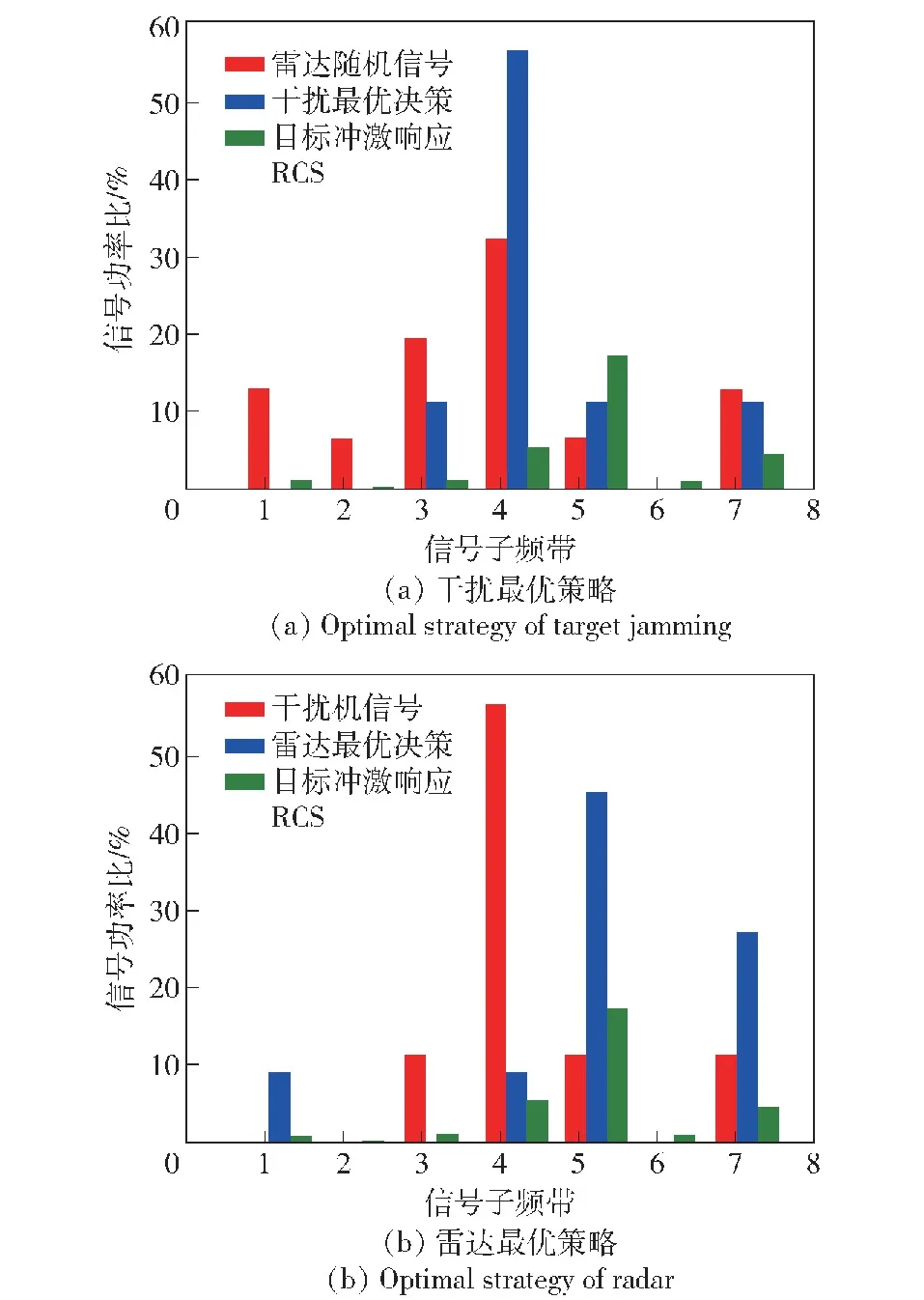
图5 雷达和干扰博弈过程二Fig.5 Game process two of radar and jamming

图4、图5均为雷达和干扰机在博弈过程中的策略对比。图4(a)中,雷达初始发射信号为线性调频(LFM)信号,此时干扰机作为博弈主导方,根据接收的雷达LFM信号,在目标冲激响应较高的3、4、5、7子频段上实施干扰,尤其在目标冲激响应最高的第5子频段分配了50%的信号功率,达到了最大化干扰效果。如图4(b)蓝色柱状图所示,雷达为实现躲避干扰的同时获取更多目标信息,选择在目标冲激响应最强的第5子频段发射全部功率,实现了对目标的有效探测。图5(a)中雷达发射随机信号,干扰机在雷达信号较强且目标冲激响应较高的3、4、5、7子频段上实施干扰,为了有效压制雷达信号,将更多的干扰功率分配给雷达信号最强的第4子频段。如图5(b)蓝色柱状图所示,雷达则在干扰信号较弱且目标冲激响应相对较高的1、5、7子频段分配了90%的信号功率,实现抗干扰的同时最大程度地提升信号的SINR。

由图、图5可见,雷达和干扰双方均可利用此模型实现最优决策。

3.2 时域波形合成

为将本文方法更好地应用于实际雷达探测系统,提高目标检测性能,需产生雷达频域最优波形策略的时域发射信号。目前获取生成信号时域特性的方法很多,最简单的方法是直接快速傅里叶逆变换(IFFT)方法,对最优幅度谱进行IFFT变换,然后对变换后的信号进行幅度归一化处理,但该方法合成的时域信号与最优策略存在较大差别[31]。固定相位技术是合成非线性调频信号的常规方法,使用牛顿法计算数值解,推导复杂。Jackson等[32]使用迭代变换方法(ITM)生成恒定包络时域信号,频谱拟合效果最好。因此本节采用ITM拟合频域最优策略的时域信号。根据图4频域最优雷达和干扰策略合成时域信号,并验证其频域特性,结果如图6、图7所示。

图6 雷达策略Fig.6 Radar strategy

图6(a)、图7(a)描述了合成时域信号的实部图、虚部图、幅度谱和相位谱;图6(b)、图7(b)为验证时域波形的频域特性结果,红色虚线为本文方法设计的最优频域策略,黑色实线则表示通过ITM合成时域信号的频谱图。由此可见,合成的时域信号较好地实现了最优策略的频域特征,且具有恒包络、抗干扰等低截获性能。

3.3 性能分析

SINR是衡量雷达目标检测性能的重要参数。本节将对比最优策略波形与LFM信号、捷变频信号,分析最优波形策略的目标探测性能。

LFM信号具有大的时间带宽积,且随着时间带宽积的增大,信号的幅频特性顶部起伏逐渐减小,接近矩形;捷变频技术是指雷达发射相邻脉冲或脉冲组的中心频率在一定范围内快速变化,有部分频带被干扰时,仍能在其他未被干扰的频带上进行正常探测。这两种雷达发射信号均具有一定的抗干扰能力。将雷达信号总功率从1 W逐渐增加至30 W,通过式(7)计算3种波形策略的SINR和雷达检测概率,结果如图8所示。

图8 最优波形策略和传统雷达信号比较Fig.8 Comparison of optimal waveform strategy and traditional radar signal

雷达信号SINR随着信号总功率增加而增大。由图8(a)纵向对比可知,相同信号功率条件下,LFM信号SINR最小,捷变频信号SINR高于LFM信号,本文方法生成的最优波形策略SINR最高,且与LFM信号、捷变频信号相比,分别提高了6.39 dB和1.12 dB。图8(b)为信号目标检测概率随信号总功率增加的变化图。由此可见,捷变频信号和本文最优信号在功率分别增加至15 W和11 W时,目标检测概率可达99%以上,而LFM信号在功率增加至30 W时,仅实现70%左右的目标检测概率。因此,可通过低发射功率实现抗干扰的同时提升雷达信号的抗截获性能。

4 结论

在对抗日趋激烈的电磁环境中,为提升雷达的探测、跟踪和识别性能,本文提出了一种博弈条件下基于强化学习的对空雷达抗干扰波形设计方法。基于马尔可夫决策过程对雷达与目标干扰间的博弈过程建模,通过策略迭代求解最优频域能量分配策略,并生成恒包络时域信号,实现博弈条件下的认知雷达波形设计。仿真结果表明,本文方法产生的最优雷达信号与LFM信号、捷变频信号相比,雷达接收机SINR分别提高了6.39 dB和1.12 dB,显著提高了目标检测性能,并可通过发射更低功率实现抗干扰的同时提升雷达信号的抗截获性能。