基于贝叶斯估计的浅海声源被动定位方法

石海杰, 李京华, 刘丽丽, 常虹

(1.西北工业大学 电子信息学院, 陕西 西安 710129; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)

0 引言

在浅海环境中,多途干涉和环境参数易变不利于目标定位,需要充分利用声场传输模型和声源先验信息改善定位效果。匹配场定位是基于声场传输模型的方法,自诞生以来,相关研究不断涌现[1-7],但该方法面临的最大问题仍然是模型失配问题,特别是在浅海条件下,建立确定性意义上的声传播模型并不容易[8]。同时,为了提高空间信息获取能力,匹配场定位常采用阵列形式接收信号,而在隐蔽性要求较高的情况下,需要的是一种利用单个水听器就能实现定位的方法。Warping变换能够提取宽带脉冲不同阶简正波信号,根据群延迟理论可以实现单个水听器条件下的目标定位[9],但实际上,窄带信号具有更好的传输特性。Zhang等[10]提出一种基于自相关函数峰值提取的无源定位方法,该方法不需要估计特征声线的相对延迟,利用单个水听器就能实现定位,但无法适应非稳定环境。 Warner等[11]利用单个水听器采用基于模型的贝叶斯估计方法实现了水声参数的反演。Ren等[12]采用贝叶斯滤波方法,跟踪海底环境参数,高飞等[13]利用贝叶斯方法进行地声参数反演,该类方法能有效地解决环境参数非平稳变化的问题。Guo等[14]提出一种基于稀疏贝叶斯学习的鲁棒水声信道估计算法,用于冰下信道参数估计,仿真结果表明,所提出的迭代算法具有较高的估计精度。以上基于贝叶斯估计的水声信号处理方法,虽未涉及定位方面的研究,但该理论却是适合于水声定位的。贝叶斯估计理论是一种基于统计模型的参数估计方法,由于可以通过时间累计效应来拓展空间信息的缺失,可以采用单个水听器对目标进行定位。Ogiso等[15]利用递归贝叶斯滤波方法在室内环境条件下,利用方向标辅助方法,实现移动机器人自主定位。王彪等[16-17]将贝叶斯理论应用到多目标方向估计问题中,利用多矢量稀疏贝叶斯学习算法重构信号空间谱,建立未知稀疏源信号的压缩感知模型,仿真结果表明该方法具有较高的空间分辨率和估计精度。

总之,在浅海环境条件下,声信号在传播过程中受到环境的影响尤为严重,多种状态的海面和海底参数的相互作用导致了具有复杂空间干涉结构的声场。而当低频窄带声源移动时,声场的空间复杂调制特性转变成固定点接收信号的时间幅度调制特性。贝叶斯估计理论是一种利用概率密度函数描述声场模型的方法,参数估计结果采用后验概率的形式给出,能够有效克服随机环境对定位结果的影响,并通过时间累计效应来拓展空间信息的缺失,实现单个水听器对目标进行定位。因此,基于贝叶斯估计的水声目标定位方法的建模与求解是本文的主要研究内容。

1 浅海水下随机声场建模

1.1 信号传输几何模型

信号传输几何模型如图1所示。图1中,H为海水深度,d为水听器布放深度,ρw、cw为海水密度和声速,ρb、cb为海底密度和声速,声源S以径向速度v[n]运动,n为离散时间,z[n]、r[n]分别为声源深度和距离,a[n]为声源发射的声信号,y[n]为水听器接收到的信号,Q为静止不动的水听器。

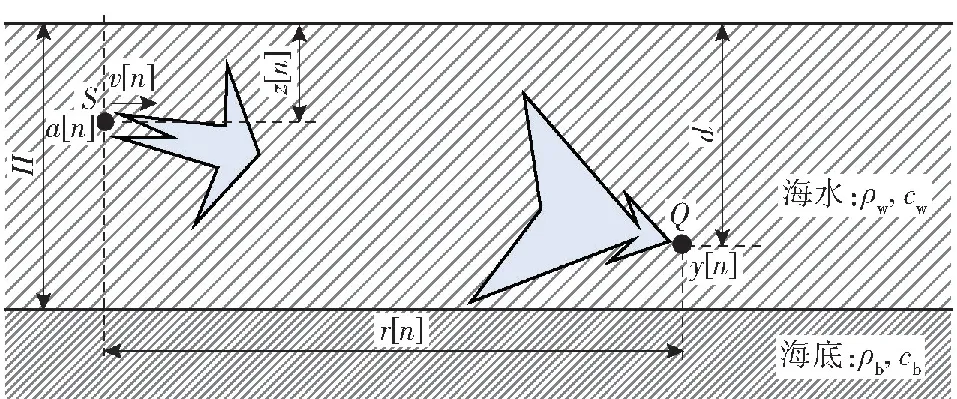
图1 信号传输几何模型Fig.1 Geometric model of signal transmission

声源发射的声信号为

a[n]=As[n]cos (2πf0n+φ0)

(1)

式中:As[n]为声源声压幅度;f0为原始频率;φ0为初相。声源状态矢量s[n]包含四个分量:r[n]、v[n]、z[n]、As[n],目标定位通过估计r[n]、z[n]实现。水听器接收的信号为

y[n]=A(s[n])cos (2πfdn+φ0)+w[n]

(2)

式中:A(s[n])为接收信号声压幅度;fd为接收信号频率;w[n]为环境噪声。传输衰减用(传输模型)x[n]表示,则对于已知固定位置的水听器:

A(s[n])=As[n]x[n]

(3)

1.2 声场概率密度模型

利用信道的统计特性,以概率密度函数描述声场传输模型,是解决环境参数非稳定的有效方法。概率密度函数估计有参数化方法和非参数化方法,核密度估计(KDE)是典型的非参数化方法。KDE法不事先设定随机过程的分布规律,是一种从样本本身出发研究数据分布特征的方法,因此理论上KDE法适用于任何复杂随机过程的概率密度函数的求解。假设利用蒙特卡洛法,根据样本数据统计获得的未知概率密度函数为f(x)(样本分布直方图),KDE方法的目的就是按式(4)构造一个概率密度函数,尽量去接近f(x)。

(4)

式中:m为核函数个数;κ(x-xi;w),i=1,2,…,m为核函数,xi为随机样本,w为核函数宽度。核函数可以是均匀核函数、三角核函数、高斯核函数等。理论上任何平滑形式的峰值函数均可作为KDE的核函数,只要满足函数曲线下方的积分面积为1即可。考虑到函数在波形合成计算上的易用性,也考虑高斯分布的普遍适用性,因此选择使用高斯曲线作为KDE的核函数。高斯核函数可表示为

(5)

核函数都是以样本点xi为均值、以w为方差的高斯分布。核函数宽度w能够控制结果曲线的整体平坦程度,也就是样本点数据在概率密度曲线形成过程中所占的比重。w越宽,样本点在最终形成的曲线形状中作用范围越大,曲线就越平坦。反之,w越窄,样本点在最终形成的曲线形状中作用范围越小,结果曲线就越陡峭。实际上,这也表明估计得到的概率密度是许多样本点分布直方图平滑的结果,这也是核密度估计方法适用广泛的原因。

核函数宽度w按式(6)确定[18]:

(6)

式中:σx为随机变量x的标准差。

2 基于贝叶斯估计的目标定位方法

2.1 贝叶斯估计水声目标定位方法建模

基于贝叶斯估计的水声目标定位方法,就是在已知水听器位置的条件下,利用声场的概率密度模型和接收信号y[n],确定声源状态矢量s[n]。根据声场概率密度模型可以确定以声源状态矢量为条件的概率密度f(x[n]|s[n]),即先验概率密度,再结合接收信号y[n]提取的信号幅度A(s[n]),利用贝叶斯滤波方法求后验概率f(s[n]|x[1],…,x[n])。 采用后验概率最大化函数作为参数估计的求解条件,则声源状态矢量估计值为

(7)

根据贝叶斯公式,有

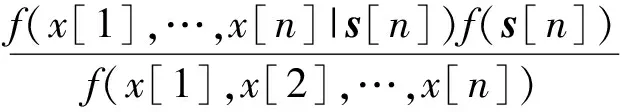
(8)

根据条件概率公式和乘法公式,式(8)变形为

(9)

式中各函数含义如下:

①f(s[n]|x[1],…,x[n])为声源状态矢量后验概率,表示接收到信号为x[1],…,x[n]时声源状态矢量s[n]的概率密度,概率密度最大位置就是声源位置。该函数就是贝叶斯估计方法最终要求的结果,反映的实质是利用接收信号确定声源状态。

②f(x[n]|s[n],x[1],…,x[n-1])表示声源状态矢量为s[n],并且已经接收到x[1],…,x[n-1]条件下,再次接收到x[n]的概率密度。声场中某点接收的信号由声源状态矢量和传输模型决定,与该点之前接收的信号无关,因此

f(x[n]|s[n],x[1],…,x[n-1])=f(x[n]|s[n])

(10)

式中:f(x[n]|s[n])称为先验概率,通过声场概率密度模型确定。该函数反映的实质是在不同声源状态条件下,能够接收到x[n]的可能性有多大。

③f(s[n]|x[1],…,x[n-1])表示当接收到信号为x[1],…,x[n-1]时,声源状态矢量s[n]的概率密度,实际上就是前一时刻的后验概率。在贝叶斯估计理论中,该函数即表示前一迭代过程的结果,又是后一迭代过程的输入,反映了估计结果不断更新校正的过程。

④f(x[n]|x[1],…,x[n-1])表示不考虑声源状态情况下,n-1时刻以前声场中某点已经接收到x[1],…,x[n-1]条件下,n时刻再次接收x[n]的概率密度。由于该函数与声源状态无关,根据无源波动方程(齐次)可知该函数应为一个常数,可以假设

f(x[n]|x[1],…,x[n-1])=1/η

(11)

式中:η为一个常数,满足后验概率对状态矢量的积分为1。在进行后验概率的求解过程中,可以先假设为1,求出后验概率后,后验概率归一化常数的倒数就是η的值。将式(10)、式(11)代入式(9),整理得

f(s[n]|x[1],…,x[n])=ηf(x[n]|s[n])f(s[n]|x[1],…,x[n-1])

(12)

用全概率公式展开f(s[n]|x[1],…,x[n-1]),根据状态更新过程的马尔可夫性,得

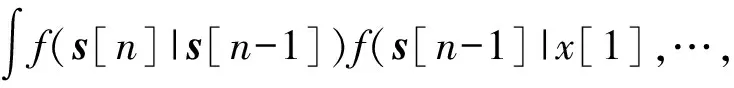
(13)

至此,得到了递归形式的后验概率模型,如式(13),也称为贝叶斯滤波公式。由于积分运算的存在,递归过程很难求得封闭形式解,需要研究有效的求解方法。

2.2 贝叶斯滤波问题的求解

观察式(13),可以发现贝叶斯滤波最大的问题在于积分的求解,由于存在时间上的迭代,很难解得封闭形式解。对声源状态矢量离散化,通过求和解决积分问题是很好的思路,将声源状态矢量离散化成多维网格,认为单一固定网格内的状态矢量的概率密度为常数。相当于利用离散的概率直方图代替真实的状态矢量概率密度函数,因此也称为直方图滤波。假设将声源状态各分量离散成Kr、Kv、Kz和Ka点,下标r、v、z、a分别对应声源距离r[n]、速度v[n]、深度z[n]和声压幅度As[n],则总网格数为K=KrKvKzKa。设第k个网格的状态矢量为sk,式(13)变成:

(14)

式中各函数含义如下:

①P(sk[n]|x[1],…,x[n])为离散形式后验概率,表示当声场中某一固定点接收到信号x[1],…,x[n]时,声源状态矢量为s[n]=sk的概率。

②P(x[n]|sk[n])为离散形式先验概率,表示在n时刻,声源状态矢量为sk条件下,声场中对应点处接收到x[n]的概率。

③P(sk[n]|sj[n-1])为状态转移概率,运动目标的状态更新过程可用如下方程表示:

s[n]=Ans[n-1]+εn

(15)

式中:An为状态转移矩阵,

(16)

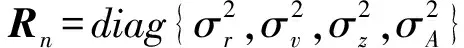
(17)

当n=1时状态转移概率变成声源状态矢量的初始分布,可以用均匀分布表示,因此

P(sj[0])=1/K,j=1,…,K

(18)

④P(sj[n-1]|x[1],…,x[n-1])是前一时刻的后验概率,也是后一时刻迭代的输入。

⑤η1为一个常数,满足后验概率对状态矢量的求和为1。

以上推导过程,将贝叶斯估计问题进行了离散化,式(14)就是贝叶斯滤波问题的数值解,该方法解决了状态矢量积分难于求解的问题。

3 实测验证与仿真分析

3.1 SWellEx-96实验说明

SWellEx-96系列实验是1996年5月在圣地亚哥海岸附近进行的,其中的S5实验拖曳深度为9 m的声源以2.5 m/s速度运行,采用海底布放的水平阵列接收(SHLA)。由于实验信息记录完备,GPS数据完整,实验数据质量较高,非常适合于浅海环境条件下目标定位算法的分析和验证。实验海域海深约200 m,SHLA布放深度198 m,本文利用SHLA中3个阵元接收的数据进行验证。实验声源含多个频率的线谱,本文利用最低频率109 Hz信号,详细环境参数可参考http:∥swellex96.ucsd.edu/index.htm。

3.2 声场概率密度函数估计结果

SWellEx-96实验提供了51组声速剖面数据,假设海水深度服从范围180～200 m、间隔为1 m的均匀分布,声速剖面和深度任意组合,构成包含1 071个样本的随机环境参数,利用Kraken程序仿真 1 071个对应的声场样本,KDE方法根据这些样本可以估计声场概率密度模型。图2所示为假设将水听器固定在(0 km,198 m)处(对应S5实验中SHLA阵列布放位置),声源在声场中不同位置时仿真的声场结果,声源幅度为1,声场声压对功率归一化。其中,图2(a)为1 071个样本声场中的任意一个,图2(b)、图2(c)为对1 071个样本求均值和方差而得到的平均声场和方差声场。由仿真结果可以看出声场中存在由干涉造成的明暗相间的条纹。仿真过程中发现不同环境参数对应的干涉结构不同,而干涉结构的存在会影响到定位结果的精度。从图2(a)、图2(b)、图2(c)的对比中可以看出,平均声场比样本声场要平滑许多,因为单个样本是有随机性的。据此现象可以想到,利用测量数据进行目标定位时,获取的实测数据相当于随机过程的一个样本,一定存在随机性,因此需要一种能够利用模型的统计特性辅助定位方法来克服这种随机性;从仿真的方差声场中可以看出声源靠近水听器时所产生的声场的离散性较大,随机性较强,这是因为声源与水听器距离越近,干涉效应越强,较小的环境参数变化也会造成较明显的干涉结果,表明两者距离靠近并不利于提高定位精度。

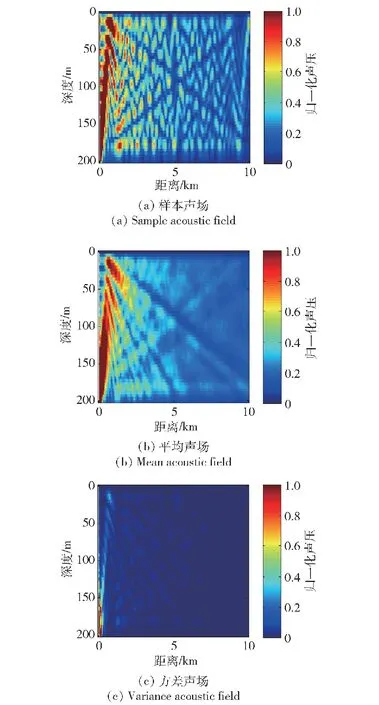
图2 归一化声压场仿真结果Fig.2 Simulation results of normalized sound pressure field

图3所示为声场概率密度估计结果,其中包含声源靠近水听器、声源在海面远场这些特殊位置的估计结果,也包括典型的一般位置(声源在中间深度,中间距离)的估计结果。从样本的绿色柱状直方图对比可以看出:1)不同位置的直方图是不同的,同一区域的直方图也不同,特殊位置与一般位置的直方图都是随机的,没有可观察到的一般规律可遵循;2)近场、特别是声源靠近水听器位置处的直方图更不规律,更容易出现多峰情况,表明这些位置声场信号的随机性更强;3)在仿真过程中发现临近位置的直方图区别可能也很大,这是由声场干涉结构决定的,干涉结构的纹理越细,声场随机性越强,这也再次表明只有基于统计特性的信号处理方法才能适用于此处。图3中的红色划线表示核密度方法估计的概率密度函数,与高斯模型和最大熵估计得到的概率密度模型对比可以看出:高斯模型法得出的概率密度函数始终保持高斯函数固有的钟形脉冲形式;最大熵法好于高斯模型法,但对多峰分布的适应能力也不强;核函数方法估计出的概率密度函数在不同情况下都有很好的适应性,即使样本直方图分布具有多个峰值,估计结果与样本分布也匹配得很好,因此本文采用KDE方法进行声场概率密度函数估计。

图3 概率密度函数估计结果Fig.3 Estimation results of probability density function

3.3 SWellEx-96实验数据预处理

为验证定位算法,以SHLA的阵元01、阵元17和阵元32作为3个独立水听器,提取它们的数据进行前置滤波(抗混叠)、降采样、混频、滤波处理,最终提取的经过传输调制的幅度值,作为A(s[n])的估计值。图4所示为以阵元01为代表的预处理结果图,原始数据有50 min时长,选取5 min进行展示,原始数据频域图中能够很清晰地看到有109 Hz和112 Hz信号的存在,由于声源是移动目标,线谱被展宽了。通过处理后时域、频域信号可以看出109 Hz信号有效地被提取出来。

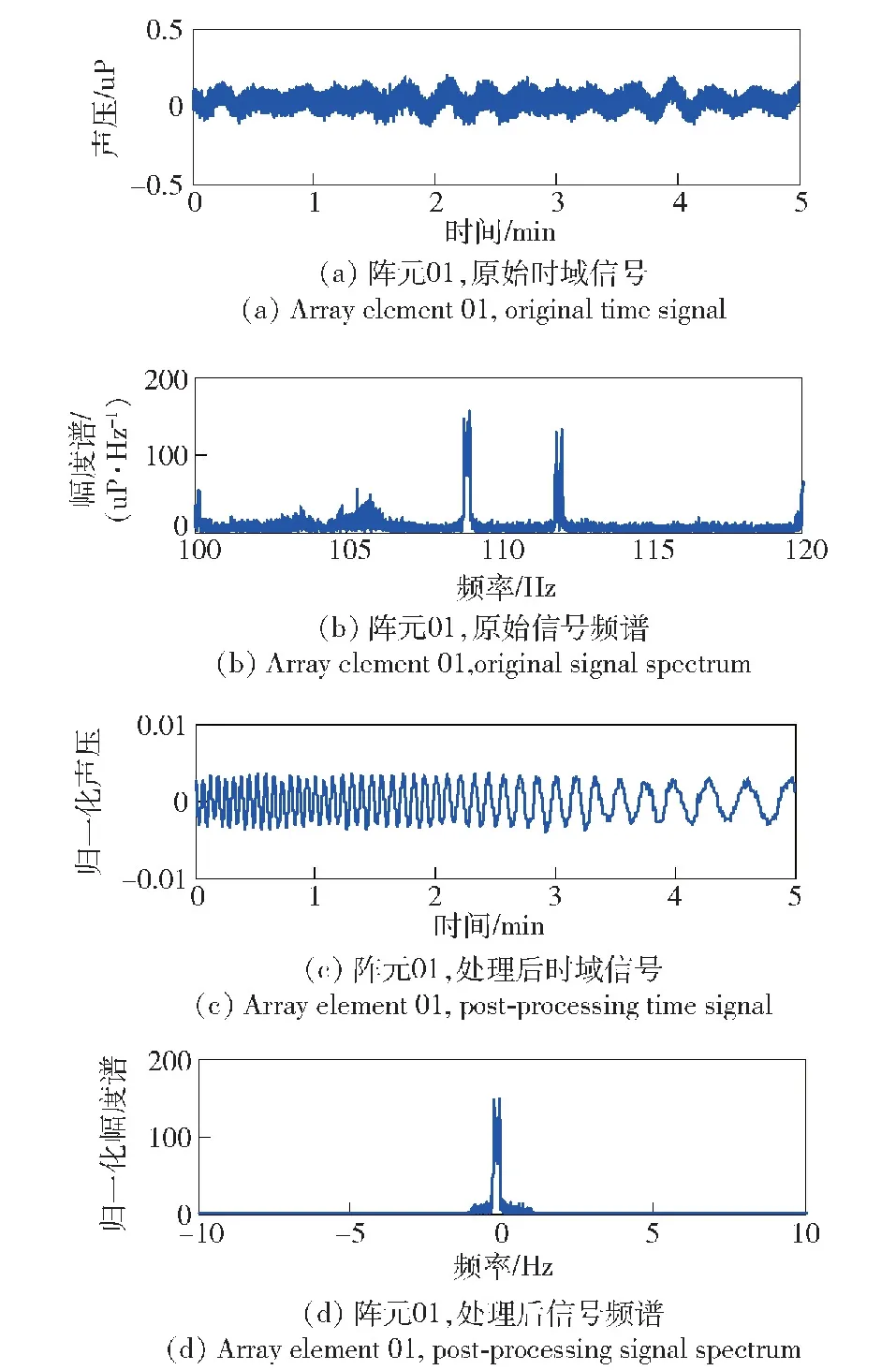
图4 实测数据预处理Fig.4 Pre-processing of measured data

图5所示为仿真的模型声场(Kraken)信号与阵元01实测数据声场信号随距离衰减的对比图。由图5可以看出,实测的真实值相当于随机过程的一个样本,与均值相比信号的随机起伏明显更大,但都是在最大值和最小值之间变化的,并且能够看出实测信号与仿真信号衰减的总体趋势基本吻合,都是由近及远衰减变大,同时伴有由干涉现象引起的幅度起伏。实测信号随机性更强还有实际测量环境噪声的影响,仿真信号并不考虑噪声,其信号幅度变化会更平顺一些。另外可以看出,实测信号的干涉结构和信号幅度与仿真信号并不匹配,特别是远场信号幅度差别更大。信号幅度的差别主要是因为实测环境的背景噪声造成的,远场时信噪比降低,幅度差异更大。正如前文所述,干涉结构的差异是由单次测量的随机性造成的,这也正是本文采用基于统计理论的贝叶斯估计方法进行目标跟踪和定位的原因。此仿真结果,一方面表明了声场模型的有效性,另一方面表明了采用概率密度模型描述声场的必要性。

图5 阵元01实测数据传输损失Fig.5 Transmission loss of measured data from array element 01

3.4 基于贝叶斯估计的水声目标定位结果

声源状态矢量按表1参数离散化,声源幅度为归一化声压幅度。信号预处理时将实测数据采样率降为1 000 Hz,因此T=0.001 s,状态更新噪声参数按照表2取值。根据式(17)和式(18)可以确定状态转移概率和初始状态分布,根据概率密度函数可以确定先验概率,根据式(14)可以进行后验概率迭代,根据式(7)可以确定目标位置。

表1 声源状态矢量参数

表2 状态更新参数表

定位结果如图6和图7所示,图6为三阵元分别在3个时刻的定位结果,图中蓝色圆圈中心位置代表声源的真实位置,红色十字中心位置是该时刻的定位结果,灰度图表示该时刻目标在定位区域内各点可能出现的后验概率。图7为定位结果相对误差随时间的变化情况。综合观察图6和图7可以得出如下结论:1)表示概率分布的灰度图以一个具有较大值区域(灰度较暗的区域)的方式跟进目标真实位置,最大概率值点与该区域有较高的一致性,而非某些突兀的概率奇点作为定位结果,能表明本文方法是一种具有较好可靠性的方法;2)开始时刻的定位精度没有后续时刻定位精度高,这是因为开始时刻声源状态矢量采用均匀分布方式表示,后续时刻声源状态矢量用前一时刻后验概率表示,随着时间的推进,定位结果将得到不断纠正,越来越接近真实目标位置;3)距离定位结果的稳定性好于深度定位结果,这是因为声场模型干涉结构在距离方向的尺度远大于深度方向的尺度,尺度越小干涉越复杂,定位越困难,稳定性越差。

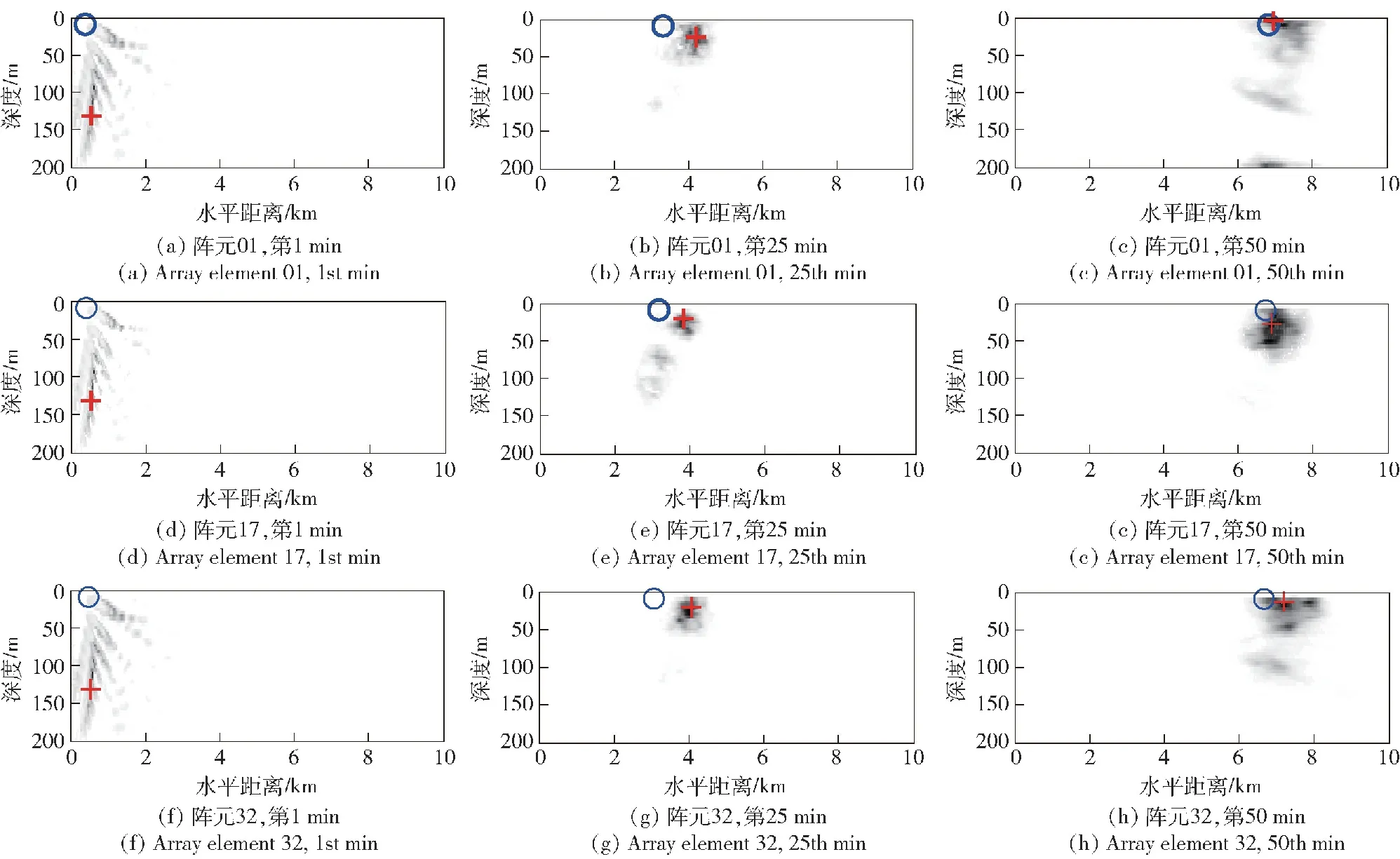
图6 各阵元不同时刻定位结果Fig.6 Localization results of each array element at different times

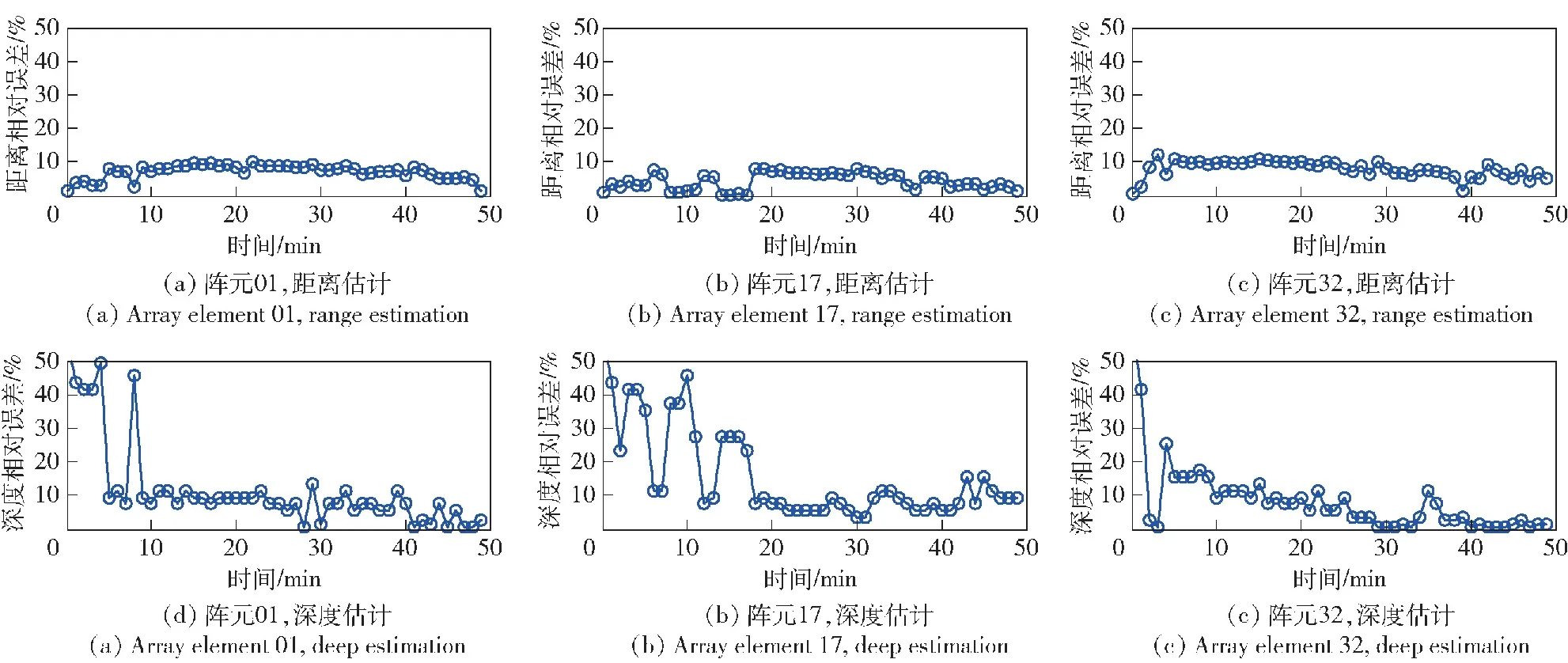
图7 定位结果随时间变化情况Fig.7 Variation of localization results with time

以上结论中1)、2)比较容易理解,3)的理解可以参考图8和图9。图8为将图2的声场样本变换显示比例,尽量放大距离方向显示比例,并截取一部分显示的结果,此时距离方向的缩小比例仍然是深度方向缩小比例的数倍,但从图像的干涉条纹中已经能够清晰地看出深度方向的干涉尺度远小于距离方向的干涉尺度。干涉条纹尺度越小,表明干涉结构越复杂,也越不利于定位。再观察图9所示的二维归一化声压传输损失,选100 m深度处归一化声压随距离的传输损失和5 km距离处归一化声压随深度传输损失情况,并绘制到同一坐标下,可以看出深度方向干涉结构尺度和距离方向干涉结构尺度的对比关系显示得更加清晰。

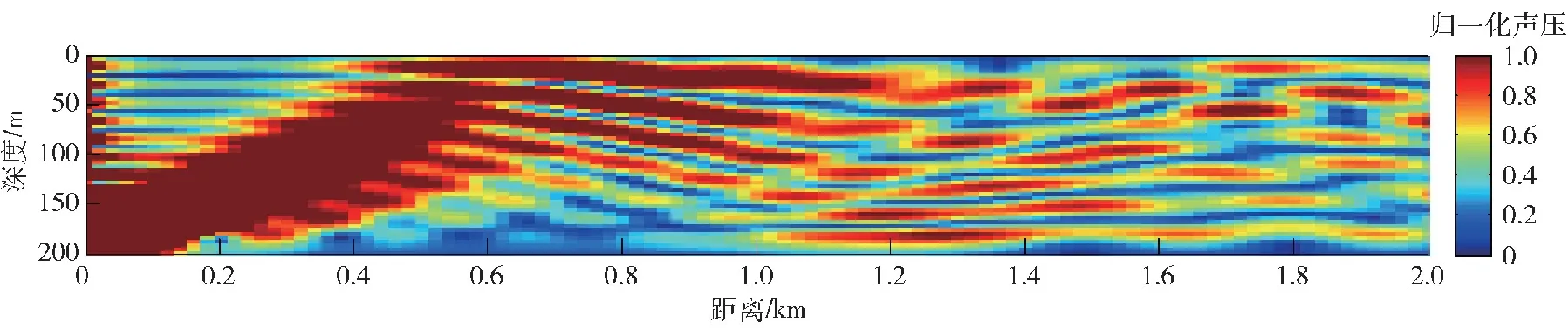
图8 三维归一化声压传输损失Fig.8 Three-dimensional normalized sound pressure transmission loss

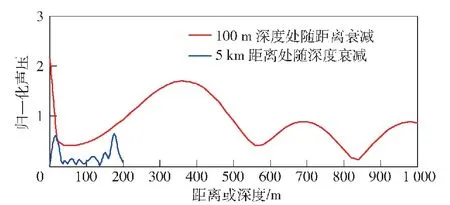
图9 二维归一化声压传输损失Fig.9 Two-dimensional normalized sound pressure transmission loss

基于以上分析,贝叶斯估计方法在定位水声目标时,距离方向定位稳定性要好于深度方向定位稳定性。实际上,浅海环境目标的深度定位一直是一个难以解决的问题。从实测数据的定位结果来看,本文方法的可取之处在于距离方向定位的稳定性,更在于能够较准确地估计目标的深度。

3.5 基于贝叶斯估计的水声定位误差

定义式(19)为距离估计相对误差,定义式(20)为深度估计相对误差:

(19)

(20)

式中:rmax-rmin为距离定位范围,rmax-rmin=10 km;zmax-zmin为深度定位范围,zmax-zmin=200 m;N为估计次数。根据式(19)和式(20)可以得到表3的结果,表3中均值是指3个阵元相对误差的平均值,表明本文研究的定位方法,深度定位误差为12.04%,距离定位定位误差6.47%,深度误差大于距离误差,与之前分析的结果是一致的。由于分析的样本包含开始阶段误差较大的估计结果,实际定位效果要好于上述结论。

表3 定位结果相对误差表

4 结论

贝叶斯估计原理的实质是试图用所有己知信息来构造系统状态变量的后验概率密度,即用系统模型预测状态的先验概率密度,再使用最近的量测值进行修正,得到后验概率密度。这样通过观测数据的不断更新来递推计算状态参数,由此获得状态的最优估计。本文提出的基于贝叶斯估计水声目标定位方法,主要是用于解决非平稳过程描述和非平稳噪声去除问题。研究的重要内容之一是获得有效的先验概率密度函数,准确地表示不确定性。利用贝叶斯信号处理技术,可以利用这种不确定的知识来改进被动定位性能。另一个重要内容是根据系统的体系结构建立所需的参数估计模型,包括确定未知参数与概率密度函数的关系,还有就是确保观测量是概率密度函数所描述的随机过程的样本。最后一个内容就是后验概率的求解,也就是迭代算法的设计,通常也称为滤波算法。通过以上内容的研究,本文设计了一种有效的针对浅海环境中的运动目标定位方法。仿真和实验结果表明:在浅海环境条件下,200 m×10 km的范围内,声源目标水平距离定位精度可达到6.47%,深度定位精度可达12.04%。由于采用单个水听器就能实现运动目标定位,本文方法可用于隐蔽低耗平台对目标的定位。