端面MEFP成型及威力性能的数值模拟研究

2023-05-31杨宝良易荣成赵太勇陈智刚王维占

兵器装备工程学报 2023年5期

周滔,杨宝良,易荣成,景彤,赵太勇,陈智刚,王维占

(1.中北大学机电工程学院, 太原 030051; 2.中北大学地下目标毁伤技术国防重点学科实验室, 太原 030051;3.西安现代控制技术研究所, 西安 710065;4.重庆长安工业(集团)有限责任公司, 重庆 401120)

0 引言

多爆炸成型弹丸(MEFP)是一种基于单个爆炸成型弹丸(EFP)发展而来的高效毁伤战斗部。为了解决单个EFP对分布密度较大、防护相对较弱的集群装甲目标、地面武器设备以及人员等目标的毁伤效率不高的问题,20世纪80年代提出了MEFP的设计理念,成为战斗部技术研究的热点[1-5]。与传统的EFP战斗部相比,MEFP战斗部可以在保证一定侵彻威力的前提下,形成多个爆炸成型弹丸,且以一定的飞散方向分布在空间内,对地面集群目标、空中飞行目标以及技术类兵器进行大密度、大面积攻击,从而有效提高战斗部对目标的毁伤几率。

对于 MEFP 战斗部结构设计,Bill等[6]设计一种新型聚集战斗部,该战斗部一次起爆可形成55个质量不小于13 g的球形穿甲弹丸;Saroha等[7]则对设计的单点起爆形成多EFP战斗部进行了侵彻威力试验研究,然而对于战斗部具体装药尺寸则均未公布。国内关于MEFP的研究起步较晚,杨宝良等[8]设计了一种周围排列的MEFP战斗部,并在中心线起爆与端面起爆方式下得到了初速高、攻角小、气动性能良好的EFP;赵长啸等[2]设计了一种整体式MEFP战斗部,能产生7枚近距侵彻威力较大的弹丸,但其周边弹丸成型形态不佳,气动稳定性较差;曹明阳等[9]设计了一体式多爆炸成型弹丸战斗部,可产生17枚弹丸,并通过试验验证,但其飞散角达到了14.8°;Ma Guangsong等[10]研究了药型罩与壳体一体化设计的MEFP成型特性,结果表明采用整体设计的MEFP形态优于单独设计;LiuJianFeng[11]等研究了具有7个半球形药型罩的整体式多爆炸成型弹丸( MEFP )战斗部的成型和空间散布规律,在数值结果的基础上对MEFP的成型过程和形态进行了描述;Tao Zhou等[12]对新型环形MEFP进行成型和侵彻研究,研究表明随着轴向曲率半径的增大,其长径比减小,侵彻能力下降。

通过上述分析,前人的研究主要集中在球缺型MEFP成型特性和侵彻威力方面的研究,而对于新型结构MEFP成型影响因素、威力半径方面的研究极度缺乏。因此,本文中设计了一种新型扇形组合式MEFP战斗部装药结构,并对该种MEFP成型特性、成型影响因素进行了分析,发现该战斗部起爆后可形成一种飞散角可控且满足一定侵彻威力的周向辅助EFP。

1 结构方案及数值模型

以典型MEFP战斗部装药结构为基础,研究设计了一种新型且便于加工的组合式MEFP结构,如图1(a)所示。战斗部由组合式主辅药型罩、闭气环、主装药、壳体以及起爆装置组成。其中药型罩材料为紫铜,具体分布为:中心主罩外加12枚辅助子罩,扇形辅罩经车制、切削加工而成,工艺简单,且同一性和对称性较好;闭气环采用低密度聚合物制成的镂空结构,战斗部装配时可对药型罩进行定位,战斗部起爆后具备一定的闭气作用,具体结构如图1(b)所示;主装药为8701炸药,可采用带罩压药工艺制作,以保证各部件之间的装配精度;壳体材料为45#钢;采用装药端面中心点起爆。

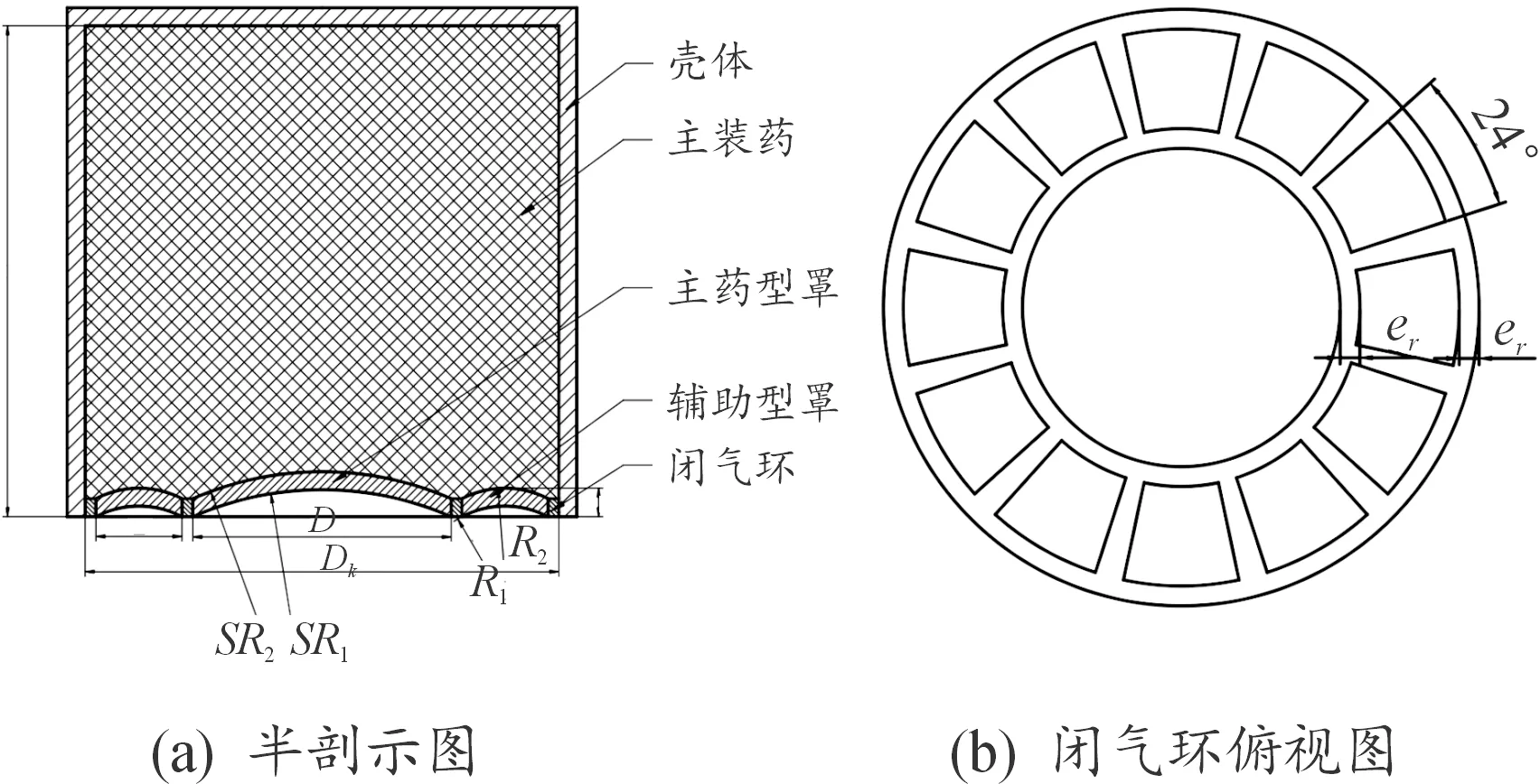
图1 战斗部结构示图

战斗部结构特征:中心主罩为等壁厚球缺药型罩,其口部直径为D,内外壁面曲率半径分别为SR1=70 mm,SR2=74.5 mm;闭气环宽度为er=4 mm;装药高度为H;装药直径Dk=120 mm;壳体厚度为5 mm;单个辅罩为扇型结构,所对圆心角为24°,其内外壁面曲率半径分别为R1、R2,厚度e=R2-R1,罩顶高度为h,径向跨度为L。

采用ANSYS/LS-DYNA有限元数值模拟软件对MEFP的成型和侵彻过程进行数值模拟研究[13],研究中的仿真模型由于需要获取周向组件的成型参数,并且EFP成型过程中存在发散效应,无法进行几何上和理论上的简化,只能采用全模型。使用TRUEGRID建立1∶1三维实体模型,如图2所示。

图2 仿真计算模型

模型计算网格均采用Solid164八节点六面体单元,药型罩、装药、壳体的网格尺寸分别为1.5、2、3 mm,均采用Lagrange算法,它们之间的接触类型设置为自动面——面接触,组合式药型罩建模时分3个部分建立,分别为主罩、辅罩和闭气环(图3),其中闭气环外形特征与辅罩基本一致,其网格尺寸为0.5 mm,设定接触条件时,闭气环分别与主辅药型罩单独设置了面——面固接接触(其余接触类型均为自动面——面接触),模拟其闭气、断裂过程对MEFP成型的影响。

图3 组合式药型罩剖视示图

主装药选用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程[14]进行描述,主要参数见表1。金属材料全部采用JOHNSON-COOK材料模型[14],状态方程为GRUNEISEN,主要参数见表2。

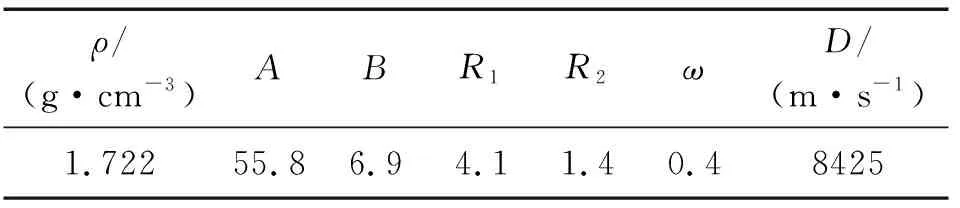
表1 8701 炸药参数

表2 金属材料参数

其中:A为屈服应力;B为应变硬化系数;n为应变硬化指数;C为应变率相关系数;m为温度相关系数。

2 MEFP成型过程

MEFP战斗部辅罩EFP成型后,会出现发散运动现象,即初始飞行过程中存在一定的初始飞散角,如图4为本次设计的端面组合式MEFP成型过程示图。从成型过程可知,辅罩EFP成型后逐渐飞散,而控制辅罩EFP初始飞散角对打击不同装甲面目标具有重要意义。

图4 不同时刻MEFP成型形态

上述成型过程主要分为3个阶段:药型罩受冲击载荷作用,罩内微元产生速度梯度,主要体现为微元之间相对运动,是辅罩弹丸自身变形的主要阶段,其次伴随着弹丸的翻转运动;罩微元之间速度梯度逐渐减小,直至不再产生相对运动,但仍有相对运动的趋势,此时辅罩弹丸外形已经基本确定,主要体现为弹丸以速度瞬心为旋转中心进行翻转,即姿态调整阶段;最终弹丸内各微元速度趋于稳定,质心不再翻转,弹丸以一定的速度及方位向外飞散,即稳定飞散阶段。选取一枚辅助药型罩,如图5(a)所示沿战斗部径向建立6个观测微元,从后处理软件中读取各个微元的受载情况,对上述成型过程进行验证分析。

由图5(b)可见,当冲击波瞬时加载在药型罩上时,观测点6626、6628、6630、6632、6634、6636由内及外依次受到冲击波加载作用,且各观测点压力曲线第1个波峰所对应时刻依次顺延,其大小也基本符合逐渐减小的趋势;同时随着时间的增长,在壳体反射稀疏波的作用下,各观测点压力曲线出现第2个极值点,其中远离壳体的观测点压力曲线中出现“台阶”,而靠近壳体区域的观测点压力曲线则出现第2个波峰,且与其相对应时刻也呈现由内及外的顺延现象。

图5 观测设置及其压力变化曲线

综上可知,当冲击波作用在药型罩的瞬间,越靠近中心的罩微元越先受到冲击载荷,且压力峰值越大,微元获得的能量越大,速度越高;而靠近壳体的罩微元受到的压力峰值较小,微元速度较低,且时间相对延迟,因此药型罩在自身变形阶段还伴随着“逆时针”翻转现象(图4 ,图6 ),而翻转过程是影响弹丸最终飞散姿态的重要因素。

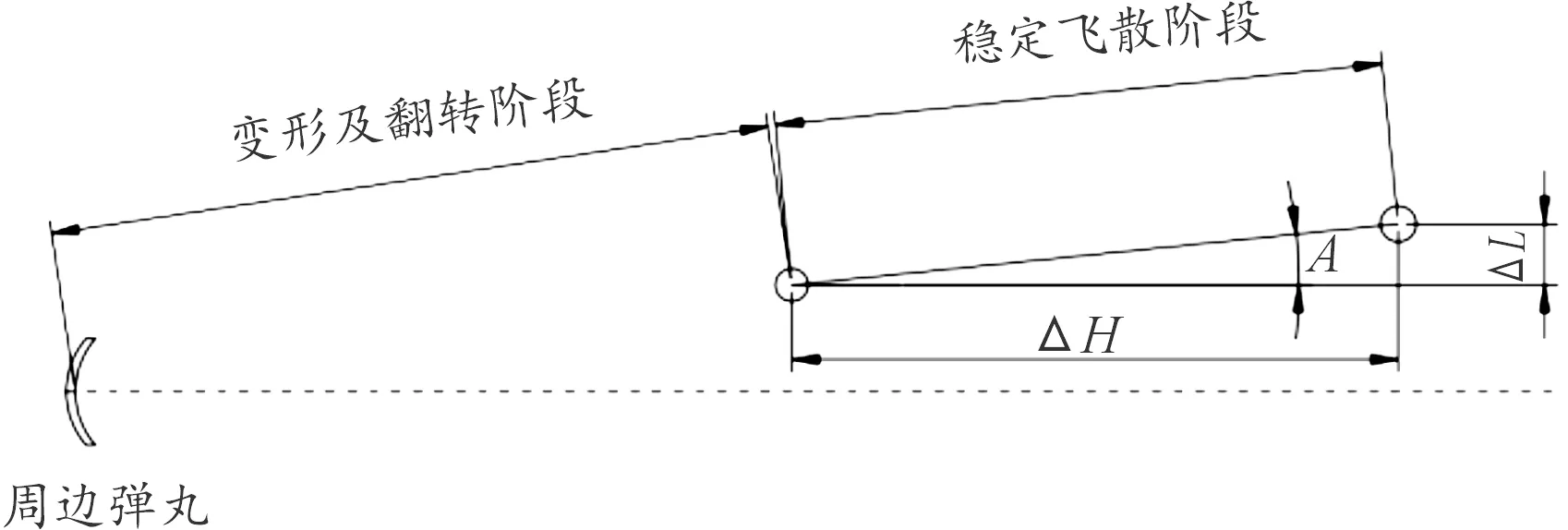
图6 弹丸飞散角测量示图

由于球面冲击波对辅助药型罩的径向驱动作用以及药型罩结构的特殊性,MEFP装药形成的辅罩EFP除了质心翻转现象外还存在一定的飞散角,如图6所示,而飞散角A的大小则是衡量MEFP毁伤面积的重要标准。

研究对比发现,主辅药型罩结构匹配性、装药特性均对飞散角和飞散形态有一定的影响,因此,以下将通过控制变量法依次改变装药长径比,辅罩罩厚度、罩顶高度、径向跨度4个变量对其成型过程及侵彻威力进行分析。

3 MEFP成型特性及侵彻威力分析

3.1 成型特性分析

3.1.1装药长径比影响

装药长径比[15]是影响EFP形态和飞散特性的重要因素,装药长径比过小会导致药型罩压垮不充分,导致EFP形态呈现“扁平状”,且速度较低,而装药长径比过大会导致药型罩过度拉伸,EFP形态呈“细长杆”形,其成型速度较高但飞行稳定性较差,因此,选取合适的装药长径比是保证EFP成型特性的重要前提。针对装药长径比对弹丸的影响设置了不同仿真研究方案,其中,取SR1=70 mm,SR2=74.5 mm,R1=35 mm,e=6 mm,h=7.46 mm,L=20 mm,装药长径比H/Dk取0.5～1.33进行数值模拟。从仿真数据来看,随着装药长径比的增大,主辅药型罩获得的能量也逐渐增大,其速度均呈现逐渐提高的趋势,其中辅罩EFP飞散角呈现先增大后减小的变化趋势(表3),成型特性曲线如图7所示。

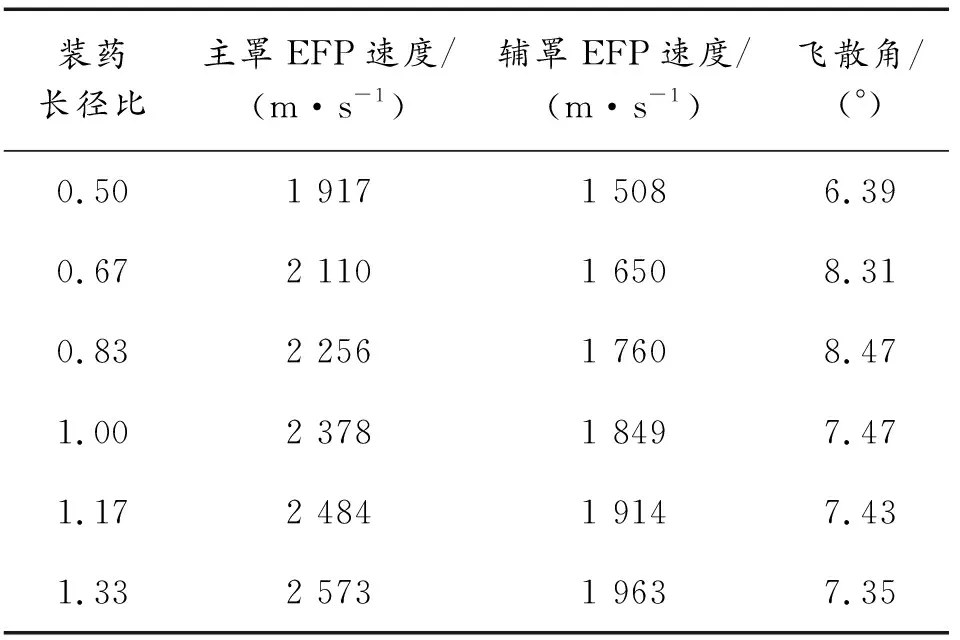
表3 不同装药长径比下MEFP成型参数

分析冲击波传播规律可知,爆轰波在药柱内以球面波传播,同时由于壳体的束缚作用,在其内侧形成反射稀疏波,随着装药长径比的增大,爆轰波对药型罩的作用次序可分为以下3种情况:主罩、辅罩、壳体;主罩、壳体、辅罩;壳体、主罩、辅罩。其中,前2种情况,随着装药长径比的增大,爆轰波与壳体反射稀疏波作用时间间隔逐渐缩短,其叠加后的波形不稳定,辅罩EFP飞散角随之增大;而爆轰波作用次序变换为第3种情况后,次序不再随装药长径比增加而变化,且叠加后的波形趋于稳定,接近平面波,辅罩EFP飞散角也随之减小。

随着装药长径比的增大,爆轰产生的能量提高,罩微元之间的速度梯度增加,拉伸现象更加明显,主罩EFP形态由“短粗杆形”向“细长杆形”变化,而辅罩EFP拳柄长度逐渐增加,其飞散形态呈现过渡变化趋势(表4)。其中当装药长径比在0.67～1时,主罩弹丸长径比适中,辅罩EFP飞散角在8°左右,且飞散姿态较好。

图7 不同装药长径比下MEFP成型特性曲线

表4 不同装药长径比下MEFP形态

3.1.2辅罩厚度影响

药型罩厚度[16]是影响MEFP成型形态的重要参数,厚度太小则在成型过程中容易发生拉伸断裂,而厚度过大时药型罩抵抗变形能力增强,不易被压垮,两者皆不能产生形态较佳的弹丸,只有选取恰当的壁厚才能成型长径比合适且形态较好的弹丸。针对辅助药型罩厚度对弹丸的影响设置了不同仿真研究方案,其中,取H/Dk=0.67,SR1=70 mm,SR2=74.5 mm,R1=35 mm,h=7.46 mm,L=20 mm,厚度e取4～8 mm进行仿真。当辅罩厚度改变时,其成型速度和飞散角也随之改变(表5)。

如图8为不同厚度下弹丸成型特性曲线,当药型罩厚度e由4 mm增至8 mm时,飞散角由5.47°单调增大至12.69°;辅罩EFP由于其质量增加,而装药量基本不变,辅罩分配的能量也基本不变,其成型速度呈下降趋势,而主罩EFP速度呈现缓慢增长趋势。

表5 不同辅罩厚度下MEFP成型参数

结合图8和表6可知,随着辅罩厚度的增大,主辅EFP之间的速度差也逐渐增大,且主罩速度始终高于辅罩EFP,二者分离过程缩短,整体闭气性能下降。其中爆轰产物由战斗部中心向外扩散,其扩散速度与二者速度差成正相关,最终导致辅罩EFP飞散角随辅罩厚度的增大而增大。同时,壳体反射稀疏波对主罩EFP的作用逐渐减弱,罩微元之间的相对位移减小,拉伸过程缩短,其外形逐渐由“锥形”向“伞形”变化,长径比减小,弹体闭合效果逐渐变差。从仿真结果来看,辅罩厚度e由4 mm变化至8 mm时,辅罩EFP的形态和飞散姿态都比较好,外形近似“拳头”,迎风面光滑,飞行阻力较小。因此,可在保证主、辅EFP飞行稳定性和有效毁伤面积的前提下,适当调整辅罩厚度,优化质量与速度的匹配性,提高极限穿深或靶后效能。

图8 不同辅罩厚度下MEFP成型特性曲线

表6 不同辅罩厚度比下MEFP形态

3.1.3辅罩罩高影响

药型罩罩高与曲率半径成负相关,而药型罩罩高关系到炸药汇聚能量的比率[16],罩高过大则汇聚能量过大,形成弹丸的长径比较大,易拉断;罩高过小则聚能效应变小,形成的弹丸长径比则过小,容易形成“馒头状”弹丸。因此,为得到外形合适的辅罩EFP,针对药型罩罩高对弹丸形态的影响设置了不同仿真研究方案,其中,取H/Dk=0.67,SR1=70 mm,SR2=74.5 mm,e=6 mm,R2=R1+e,L=20 mm,罩高h取7.27～8.68 mm进行数值模拟,主辅EFP速度及飞散角数据如表7所示。

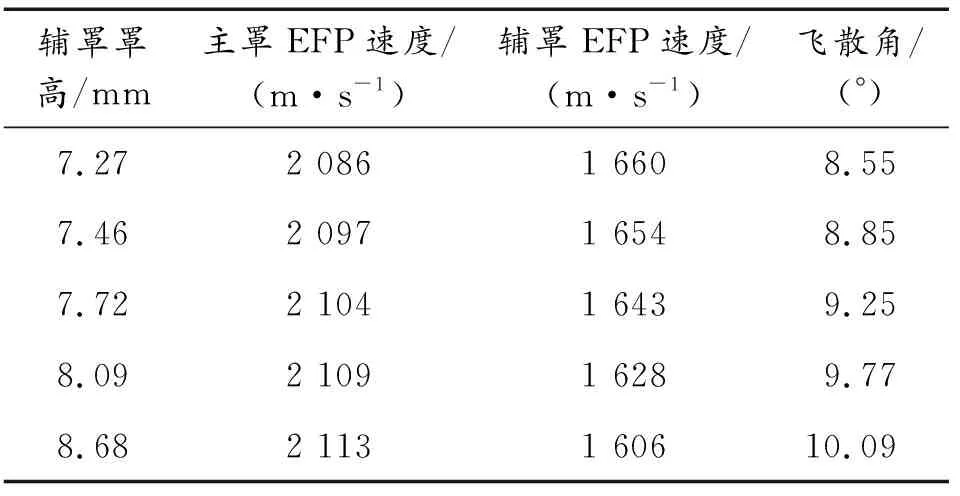
表7 不同辅罩罩高下MEFP成型参数

由图9可知,随着罩高h的增大,主罩EFP速度呈现小幅度增大的趋势,而辅罩EFP速度则呈现逐渐减小的趋势,二者之间的速度差缓慢增大,辅罩EFP飞散角也随着二者速度差的增大而缓慢增大,再次验证了4.1.2中飞散角随速度差增大而增大的规律。辅罩罩高h增大时,爆轰波加载在辅罩上时能量汇聚效应得到增强,辅罩内部微元之间速度梯度也随之增大,成型过程中拉伸现象更加明显,导致辅罩EFP拳柄长度逐渐增大,其最终形态和飞散姿态逐渐变差(表8),同时辅罩EFP自身变形阶段所消耗的能量也随着罩高h的增大而提高,使得辅罩EFP成型速度降低。由表8可知,当辅罩罩高h取值在7.27～7.72 mm时,主辅EFP成型形态较好。

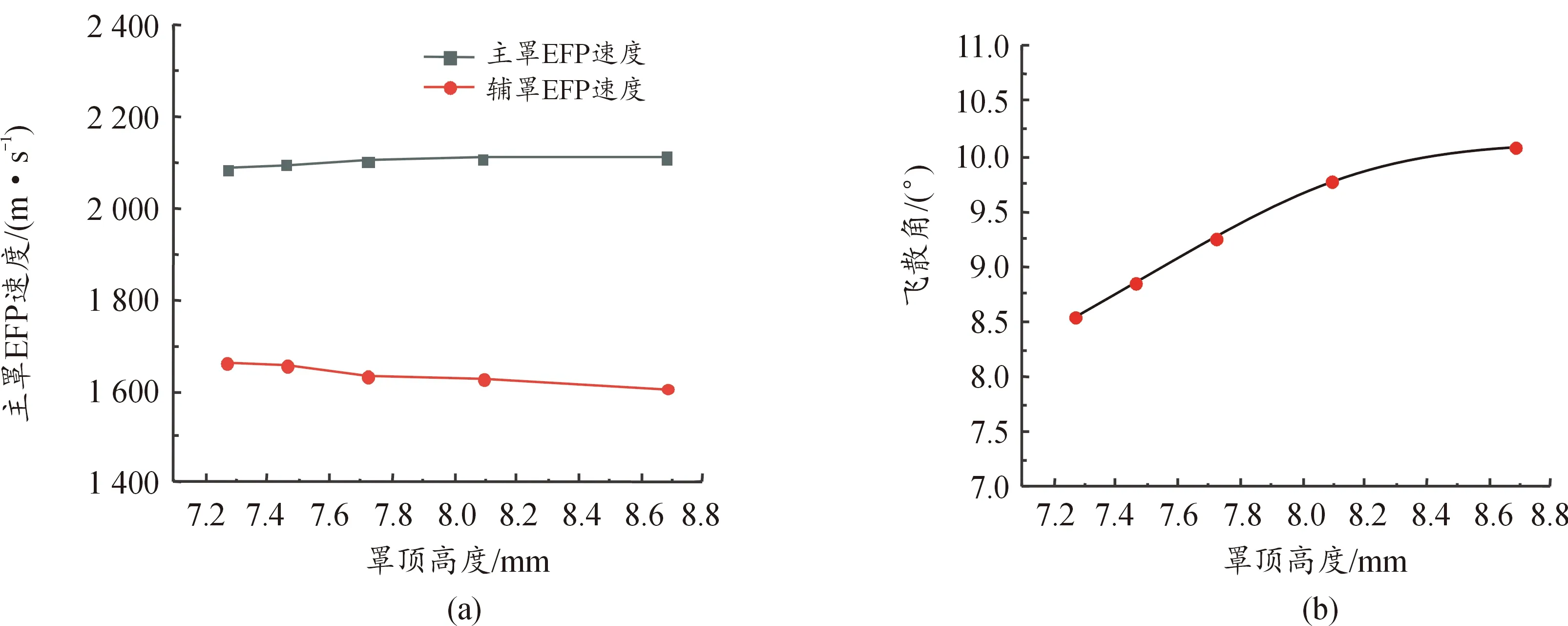
图9 不同罩高下MEFP成型特性曲线

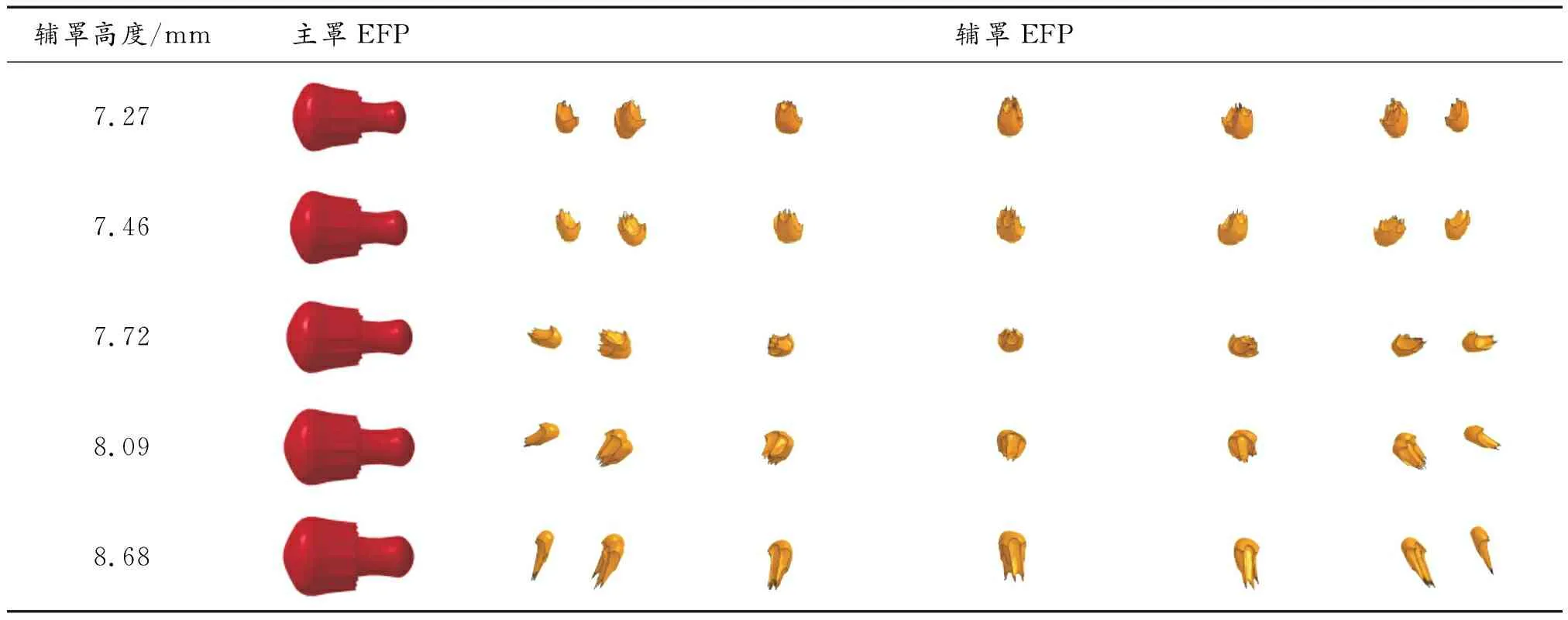
表8 不同辅罩罩高下MEFP形态

3.1.4辅罩跨度影响

辅罩跨度是影响能量分配的重要因素,而能量分配则影响到MEFP的成型形态。辅罩跨度增大,即主罩半径减小,辅罩质量及获得的能量也随之增大,主罩则与其相反。因此,为了得到合适长径比的主罩EFP和质量较大、速度较高的辅罩EFP,文中针对辅罩跨度对弹丸成型的影响设置了不同仿真研究方案,其中,取H/Dk=0.67,SR1=70 mm,SR2=74.5 mm,R1=35 mm,e=6 mm,h=7.27 mm,辅罩跨度L取16～28 mm进行数值模拟,如表9所示。

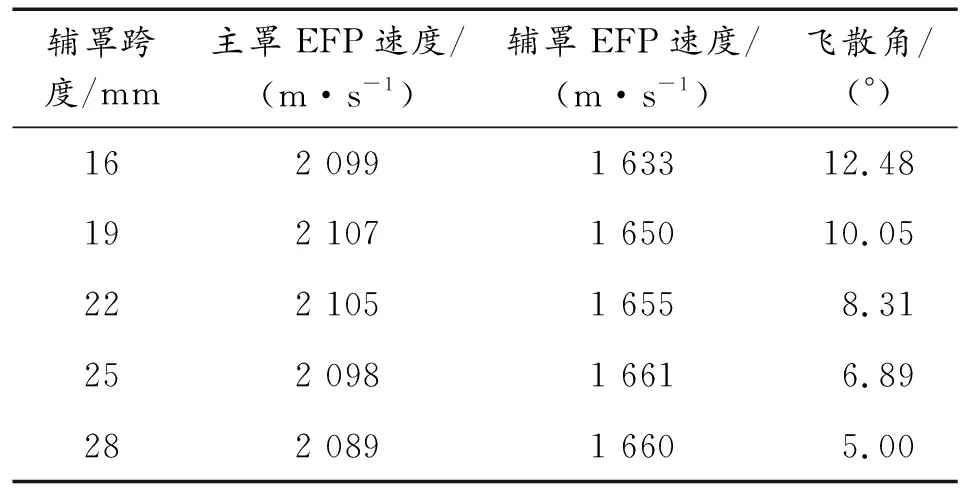
表9 不同辅罩跨度下MEFP成型参数

由图10可见,随着辅罩跨度L的增大,主罩EFP速度随之减小,而辅罩EFP的速度则逐渐增大,二者之间的速度差逐渐减小,飞散角则由12.48°单调减小至5°。当辅罩跨度L增大时,辅罩获得的能量也随之提高,而主罩获得的能量则逐渐降低。在主罩曲率半径及厚度不变的情况下,随着辅罩跨度的增大,主罩罩顶高度逐渐减小,爆轰波的汇聚效应减弱,将不利于主罩成型,其形态由“棒球杆状”逐渐变化为扁平“馒头状”(表10);辅罩EFP随着跨度的增大,质量增加,相应外形尺寸增大,拳柄长度有所增加,稳定飞散时姿态逐渐变好。

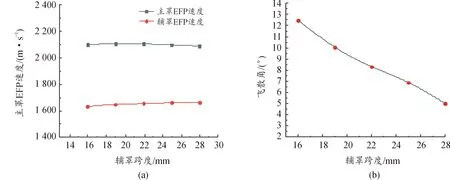
图10 不同辅罩跨度下MEFP成型特性曲线

表10 不同辅罩跨度下MEFP形态Table 10 Morphology of MEFP under different auxiliary liner spans

3.2 侵彻威力分析

经上述分析可知,研究设计的端面MEFP可在不同结构参数下形成不同飞散特性的弹丸,这将影响到MEFP对装甲目标的毁伤效能。研究选定以美国LAV-25轮式步兵战车为MEFP的侵彻目标,选取其正面首上装甲,等效靶为12 mm厚45#钢靶,靶板长200 mm,宽200 mm,厚12 mm,网格尺寸为1 mm。其中,对于主罩EFP来说,其质量和速度均高于辅罩EFP,侵彻性能也优于辅罩EFP,故不对其进行侵彻仿真。因此,研究主要对不同着靶速度下辅罩EFP对装甲目标的侵彻威力分析,端面MEFP战斗部一次性成型的12枚辅罩EFP具有较好的对称性和一致性,为提高计算效能,研究提取4种(长径比、厚度、罩高、跨度)典型成型形态下的单枚辅罩EFP进行威力分析,仿真时弹丸和靶板之间设定双向面——面侵蚀接触,计算结果如图11—图14所示。

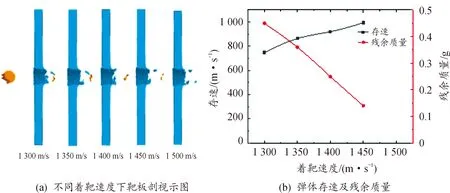
图11 H/DK=0.5,e=6 mm、h=7.46 mm、L=20 mm时,辅罩EFP质量21 g,飞散角6.39°

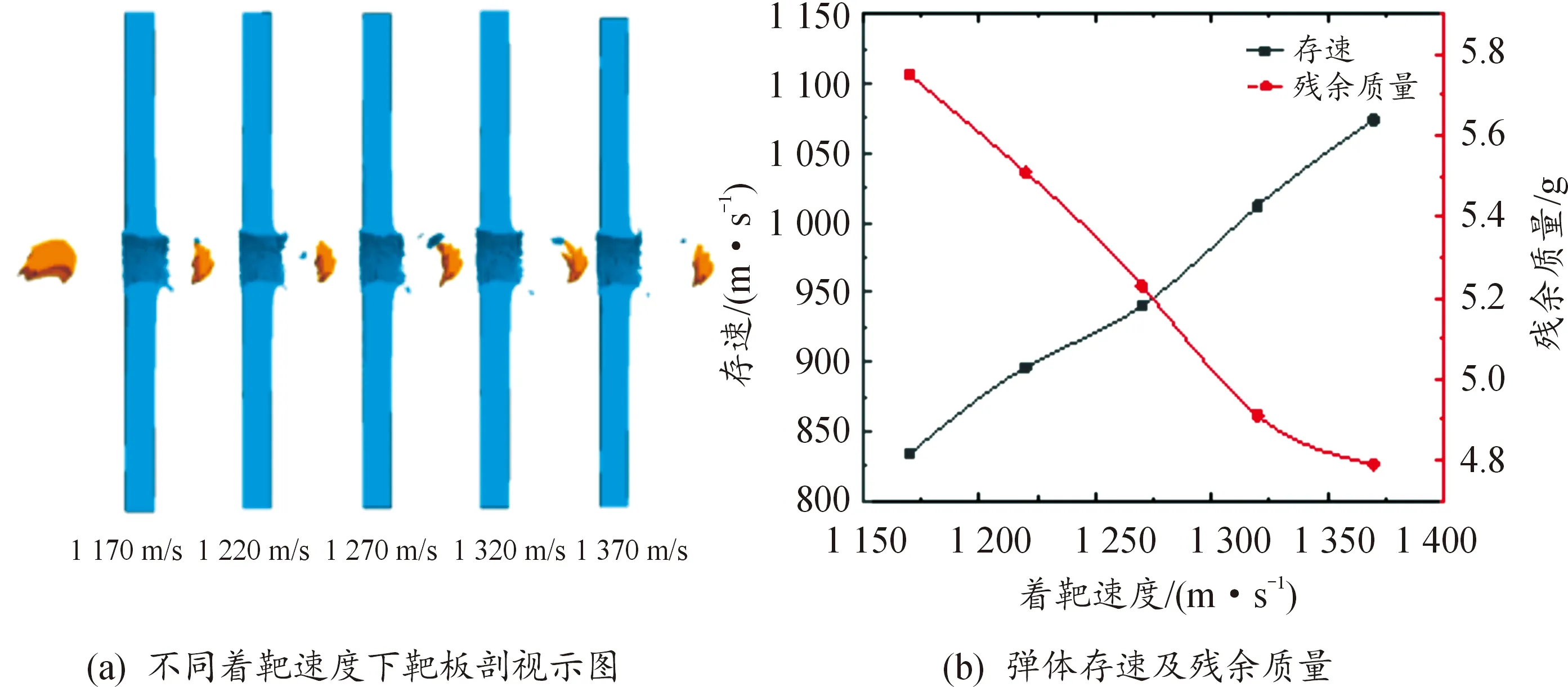
图12 H/DK=0.67,e=8 mm、h=7.46 mm、L=20 mm时,辅罩EFP质量28.1 g,飞散角12.69°

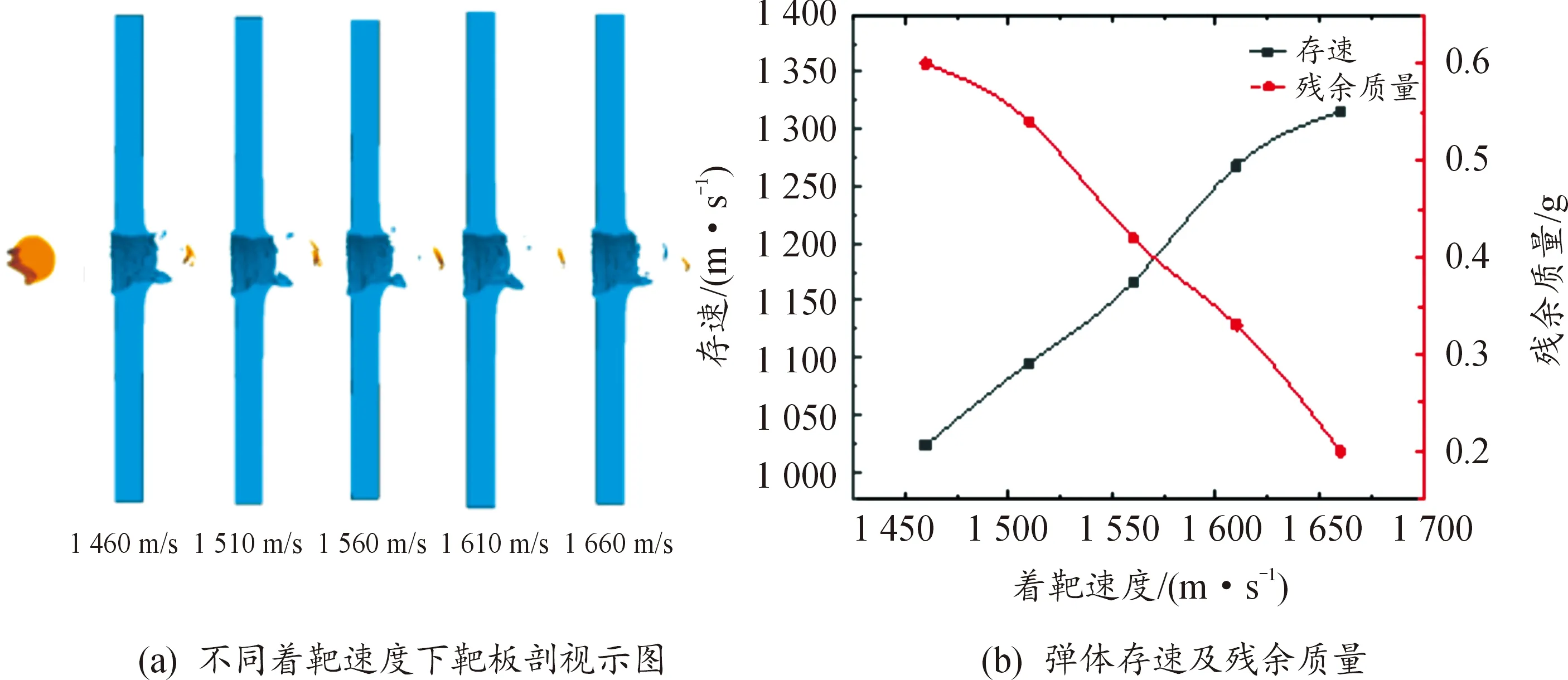
图13 H/DK=0.67,e=6 mm、h=7.27 mm、L=20 mm时,质量20.8 g,飞散角8.55°

以上4种辅罩EFP的选取依据为:辅罩EFP具备较好的成型形态;各辅罩EFP之间速度、质量、飞散角各不相同。从仿真结果来看,4种成型方案所产生的辅罩EFP均能有效穿透12 mm厚45#钢靶板,不同着靶速度下靶、弹的变形、失效规律基本一致。

从靶板剖视示图可见,随着辅罩EFP着靶速度的提高,弹孔直径呈增大趋势,同时由于辅罩EFP形似“拳状”,并带有拳柄,因此弹孔形状呈现“偏心圆台状”,且靶板入孔及出孔处均产生花瓣状的翻边;从弹体存速和残余质量随着靶速度的变化曲线来看,弹体存速与其着靶速度成正相关,而随着弹丸着靶速度的提高,弹丸触靶时的接触应力也随之提高,进而导致弹体更容易破坏失效,最终导致弹体残余质量逐渐下降(图11中着靶速度为1 500 m/s时,弹体完全失效,靶后仅有靶体冲塞形成的碎块);从飞散角大小来看,上述数据中飞散角最小为5°,最大为12.69°,均能在不同着靶速度下有效穿透靶板,进而表明研究设计的MEFP战斗部可在不同炸高、不同着靶速度下对装甲目标进行有效打击,实现毁伤半径的可控化。