基于MPSP算法的炮弹分段气动参数辨识

柴 劲,张鹏飞,张 意,齐竹昌,王天明,韩旭东

(西安现代控制技术研究所, 西安 710000)

0 引言

升阻特性作为飞行器的基本气动特性,对总体射程指标以及滑翔方案弹道设计等影响较大,因此在项目前期论证以及飞行试验中被重点关注[1-4]。在得到飞行试验数据之后,工程实践中常用2种方法进行参数辨识:一种方法是弹道复合法,即在弹道程序中对气动插值结果乘以修正系数,以使速度、弹道倾角、弹道等外弹道参数接近实测值,这种方法工作量较大且过程繁琐,辨识过程依赖工程师的经验判断,辨识结果精度有限;另一种辨识方法是通过外弹道数据求得弹体的受力信息,根据质心动力学方程直接求解升力阻力,从而得到阻力系数与升力系数的辨识值,该方法简单方便,但需要对观测数据直接进行微分,辨识噪声及辨识误差较大。

目前常见的气动辨识算法有最小二乘法[5-7]、极大似然估计[8-9]、卡尔曼滤波[10-11]以及神经网络[12-13]、蜂群算法[14]、基于学生心理的启发式优化算法[15]等智能算法。这些智能算法模型复杂且对观测量及其误差分布等信息需求较多,不利于工程应用。

本文中的辨识算法受模型预测静态规划(MPSP)[16-17]启发,该算法多用于带有终端约束的制导律设计,通过状态灵敏度矩阵建立了控制变量与终端误差的联系。本文中将待辨识气动参数类比制导律中的控制量,将辨识误差类比制导律中的终端约束误差,建立起辨识气动参数与外弹道数据误差之间的联系,通过算法自动调整气动参数,从而实现仿真弹道与外弹道数据误差小于指定精度。本文中提出的气动辨识方法简单新颖,可通过编制程序自动执行,无需通过人工手动复合弹道,减少辨识工作量,提高辨识精度,为飞行试验的参数辨识提供了一种新思路。

1 建立辨识模型

1.1 辨识动力学模型

暂时不考虑有助推发动机的情况,使用简化的纵向弹体质心动力学方程作为辨识模型,即:

(1)

式中:V、θ、x、y、q、S、cx、cy、m、g分别为速度、弹道倾角、发射系射距、发射系高度、动压、参考面积、阻力系数、升力系数、质量、重力加速度。

1.2 归一化处理

由于状态变量存在量级差异,先进行归一化处理。使用最大、最小标准化处理,归一化处理算子为:

(2)

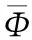
将归一化后的变量代入式(1)中,即得到归一化后的纵向质心运动模型。

2 MPSP气动参数辨识算法

2.1 算法原理

首先确定辨识步长,在每个辨识步长内应用MPSP算法进行迭代计算,使状态误差收敛至误差阈值以下,即得到待辨识参数的估计值。算法流程图如图1所示。

图1 算法流程Fig.1 Algorithm flow chart

2.2 提供辨识输入

提供外弹道数据、理论气动参数以及弹体结构参数等辨识输入。

2.3 设置辨识步长

辨识步长设置要根据飞行状态确定。若弹体全程飞行状态变化范围不大,辨识步长可以适当取长;若飞行状态变化剧烈,辨识步长需减小。

2.4 MPSP算法用于气动参数辨识

(3)

采用欧拉法对式(3)进行离散处理(为简化表示,忽略步长上标p,不失一般性,下同),得:

Xk=Xk-1+hf(Xk-1,λk-1)=Fk-1(Xk-1,λk-1)

(4)

式中:h为数值积分步长;k=1,2,…,N为离散点。

考虑式(4)全微分形式为:

(5)

式中,

(6)

(7)

(8)

(9)

令k=N,N-1,…,2,将式(5)循环代入式(9)中可得终端误差近似为:

(10)

式(10)中,

(11)

由于初始状态量为常量,故dX1=0。式(10)可简化为:

(12)

式(12)通过灵敏度矩阵Bk建立了终端误差ΔYN与待辨识参数变化量dλk之间的联系。其物理含义是,当实际外弹道数据与辨识模型的状态量间存在误差时,可通过调整辨识模型中的待辨识参数去减小该误差,直到其满足精度要求。理论上满足误差要求的辨识参数组合并不唯一。但存在一组既满足误差要求,同时与辨识初值相比变化量又最小的一组解作为“较优”的辨识结果。因此可以通过构造带有误差要求约束、最小化辨识参数变化量的优化问题。其目标函数为:

(13)

式中,Rk为权重矩阵,可对辨识参数的调整量影响进行加权。对式(12)和式(13)组成的优化问题,可通过拉格朗日乘子法转化为无约束优化问题求解。省去求解过程,直接给出最优解的解析形式为:

(14)

待辨识参数更新为:

(15)

至此,基于MPSP的气动辨识算法推导完毕。将其整理为:

步骤1提供辨识算法需要的外弹道数据、初始气动参数及弹体相关参数作为辨识输入。

步骤2设置辨识步长。

步骤4计算矩阵Bk、Aλ、Bk。

3 仿真结果与分析

3.1 仿真条件设置

以某型155 mm制导炮弹为例,验证本文中辨识算法的有效性。主要弹体参数及仿真参数设置如表1所示。其他仿真条件设置为:大气模型使用理想大气。使用真实阻力系数和升力系数进行弹道仿真,生成的速度、弹道倾角、射程、弹道高作为辨识输入。阻力系数初值使用零攻角和马赫数进行插值计算,并将插值结果拉偏+30%作为辨识初值。升力系数的初始迭代值设为零。权重矩阵Rk设为:

表1 参数设置

3.2 仿真结果与分析

3.2.1辨识精度分析

根据以上设置的仿真条件进行参数辨识。辨识步长与每个辨识步长对应的迭代次数如图2所示。总辨识步长为47步。每个步长内迭代次数在4～6次,且迭代5次的情况占多数。可见算法在弹道全段均具有较好的收敛性与一致性。

图2 辨识步长及每个步长内的迭代次数

辨识后的弹道状态量与实际弹道状态量对比如图3—图6所示。可见辨识后的弹道速度、弹道倾角、射距、弹道高与真实实际值基本重合,收敛误差小于指定精度要求。

图3 真实速度与参数辨识后的速度对比

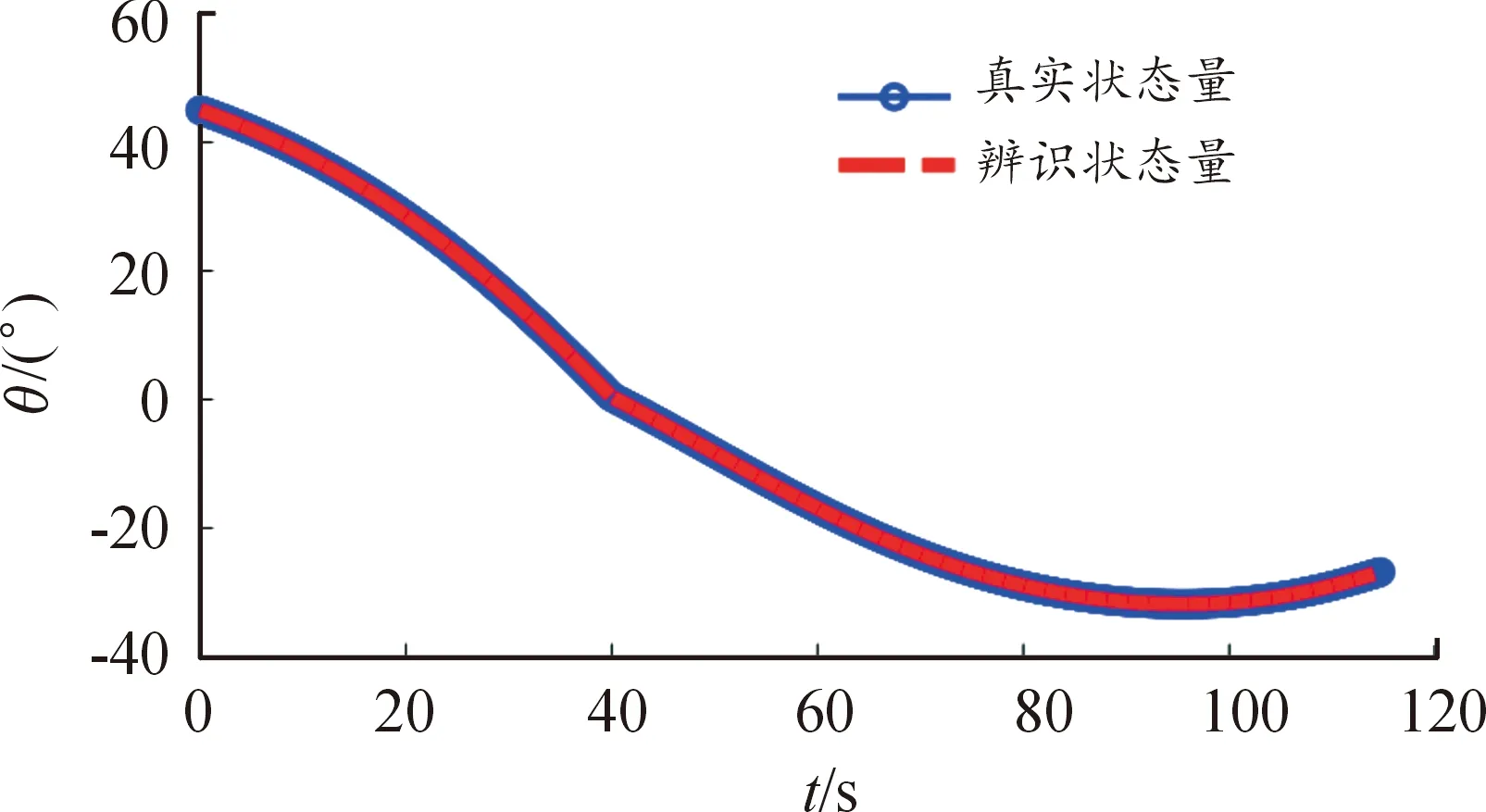
图4 真实弹道倾角与参数辨识后的弹道倾角对比

图5 真实射距与参数辨识后的射距对比

图6 真实射高与参数辨识后的射高对比

阻力系数与升力系数辨识结果如图7、图8所示。

图7 阻力系数(真实、初始值以及辨识值)对比

图8 升力系数(真实、初始值以及辨识值)对比

由图7、图8可见,在初始阻力系数、升力系数存在误差的情况下,经过迭代,辨识结果可以较好地收敛至真值。辨识误差如图9所示,无控段阻力系数误差除,在开舵等个别点达到2%,其余绝大部分飞行段误差均在1%以内。有控段阻力系数误差在0.5%以内甚至更小。升力系数误差基本在0.5%～1%以内。

图9 阻力系数、升力系数辨识误差

3.2.2算法在线计算能力分析

从算法复杂度的角度来看,假设每个辨识步长内算法迭代次数为n,每个辨识步长内的节点数记为N,则本文中算法的复杂度为O(n·N)。由于MPSP算法收敛性较快,通过几次迭代一般即可满足要求,因此迭代次数n通常较小。本文中的仿真案例对阻力系数初始值进行了30%的拉偏,升力系数初始值直接赋值为零,此时迭代次数为4～6次。考虑实际情况气动参数初值误差一般小于文中的仿真设置,因此迭代次数会更少,算法复杂度可降至O(N),具备在线计算的潜力。

从算法耗时的角度来看,在CPU为AMD Ryzen 7 4800H@2.9Hz、内存为16G的计算机上,采用Matlab 2019a编制程序对本文中算法的耗时进行了统计。结果如图10所示。横轴表示全弹道的辨识步长序号,总共47步。其中前10步为无控段辨识,每个步长为4 s,平均耗时约0.34 s;后37步为有控段辨识,每个步长为2 s,平均耗时约0.17 s。可见算法耗时较低。

图10 每个步长的耗时

4 结论

本文中提出的基于MPSP算法的气动辨识方法,是一种类比带有终端约束制导律设计思想的一种辨识新思路。通过在某型155mm制导炮弹的升阻力系数的辨识应用中证实了其有效性,并有如下结论:

1) 在仅依赖输入外弹道数据及弹体质量等必要信息的前提下,本文中算法可对升、阻力系数进行辨识,且辨识精度较高,阻力系数辨识误差小于2%,升力系数辨识误差小于1%。

2) 本文算法对待辨识气动参数初值精度要求不高。在阻力系数拉偏30%、升力系数未知的情况下,通过数次迭代即可收敛至真值附近。

3) 本文辨识算法设计简单、运算速度快,有利于工程实现。