基于SOINN增量自编码器的网络异常检测研究
2023-05-31吴署光王宏艳颜南江
吴署光,王宏艳,颜南江,王 宇
(1.航天工程大学 航天信息学院, 北京 101400; 2. 32039部队, 北京 102300)
0 引言
网络异常行为分析与识别是网络系统安全的基础,这些信息系统要想可控、可靠和有序的运行,就必须及时有效地感知网络运行状态,发现异常并消除隐患。目前研究人员在该领域已经做了大量的研究工作,其中利用机器学习的方法已经取得了较好的效果,其主要原理是构建行为特征向量并据此训练分类或者聚类模型从而实施检测[1-3]。由于无监督方法不需要带标签的数据,有效提升了异常检测的实用性,该检测方法应当满足两个假设:一是正常样本数量远大于异常样本;二是两类数据之间的差别很大[4]。无监督的方法大致可分为两类,一类是基于聚类,将训练样本划分为不同的子类,同一类样本具有相似特征,不同类样本存在较大差异[5]。另一类是离群点检测,该方法根据正常行为的特征建立用户轮廓,将当前要检测的行为特征与之进行对比,若偏离正常行为轮廓,超出一定的阈值范围,就被认定为构成入侵,否则就被判定为正常行为。汪生等[6]、Ming Zhang等[7]将OCSVM应用于异常检测,通过核函数将原始空间中相互重叠的正负样本数据投射到高维空间,从而学习到正常样本数据的边界,取得较好检测效果的同时降低了检测时间。
与传统机器学习方法相比,深度学习能够更好地从网络数据中学习非线性相关性,常见的方法有自动编码器、卷积神经网络、长短期记忆网络、生成对抗网络[8]。自动编码器(auto-encoder,AE)作为一种以重构输入样本为目标的无监督学习神经网络,能够满足现实的检测需求。其应用于异常检测的原理是通过计算测试样本的重构误差与正常行为模式的偏离程度来发现异常。研究人员在该领域作了大量研究工作且取得很多成果,例如,Gurung等[9]提出一种基于稀疏自编码器的检测模型,利用稀疏性来降低特征向量之间的关联度,在NSL-KDD 数据集上的准确率为87.2%。变分自编码器(variational auto-encoders,VAE)在异常检测任务中表现突出,在很多情况下优于自动编码器,但也存在误报率较高的问题[10]。曹卫东等[11]在优化VAE损失函数过程中融入了异常样本,模型更好地学习到正样本数据的高维分布,从而使得正负样本在低维空间中分离度加大,提高了检测精度。
随着网络模型的不断扩大,网络攻击的复杂性和隐蔽性逐渐上升,异常检测的难度越来越大。然而,自动编码器对数据的处理是批量的,模型更新时需要将新旧数据合并来重新训练,造成“遗忘灾难”问题,增加了运算和存储开销,且大数据环境下无法动态更新模型来适应新的网络环境。基于增量聚类的深度学习算法能够很好地学习数据的非线性相关性,且能实现模型的增量更新。基于此,提出一种基于改进自组织增量学习神经网络(self-organizing incremental neural network,SOINN)的增量自编码器算法,首先利用改进SOINN对原始样本进行训练,用输出的神经元近似代表原始样本特性,将输出神经元作为自动编码器的输入来训练模型,然后利用重构误差来判定是否存在异常行为,在增量学习过程中,为解决反馈更新样本中正常样本纯度不高的问题,提出一种基于距离度量的样本标签筛选机制,有效提升了模型的在线学习能力。本文所提方法在保持较高检测精度的基础上,节省了运算和存储开销,模型具备动态更新能力,能够根据网络环境变化及时学习样本特征,有利于检测复杂隐蔽的网络攻击行为。
1 相关理论
1.1 SOINN算法
SOINN是一种基于竞争学习的神经网络,算法在医疗诊断、计算机视觉、机器人智能、异常检测等领域取得了不俗的成就,有力证明了其增量学习能力[12]。算法以竞争学习的方式进行学习,输出为分布在特征空间的神经元和神经元之间的连接关系,神经元分布反映了原始数据的分布特性,连接关系构成了数据的拓扑结构。以在线的方式动态地更新网络,且不影响之前的学习效果,降低了学习过程中的存储开销。因此利用该算法来构建增量自编码器可以满足在线异常检测需求。
实验证明,单层SOINN网络与双层SOINN网络具有同样的学习效果,且训练参数进一步简化[13]。本文采用了单层SOINN网络算法,主要有以下几个步骤[14]:
1) 初始化每个学习周期内神经元集合N={c1,c2},其中c1,c2的权重为W1,W2∈Rn,W1,W2为样本集Rn中的2个随机样本,连接关系集合C⊆N×N为空;
2) 接收样本ξ∈Rn,通过计算欧式距离查找N中与ξ最近的2个神经元s1和s2,即:
其中:Wτ表示神经元τ的权重,s1和s2命名为获胜神经元。
3) 计算s1和s2的相似度阈值,对于任意神经元τ,设其邻居神经元的集合为Nτ,则τ的相似度阈值Tτ的计算公式为:
如果Ni≠∅:
否则
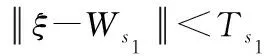
4) 若s1和s2没有连接关系,则建立2个神经元的连接,即C=C∪{(s1,s2)},将这条边的年龄设为0,即ages1,s2=0;
5) 更新年龄参数age(s1,i)=age(s1,i)+1,i∈Ns1为s1的邻居神经元;将超龄的边删除,即若age(i, j)>agemax,C=C{(i,j)},其中agemax为预定义参数;
6) 更新获胜神经元及其邻居节点的权重,
Ws1=Ws1+ε(t)(ξ-Ws1)
Wi=Wi+ε′(t)(ξ-Wi)
其中,ε(t)和ε′(t)是学习率,ε(t)=1/t,ε′(t)=1/100t,t为获胜次数;
7)若输入样本数量整除λ,即完成一个训练周期,则删掉密度较低的神经元。否则返回步骤2)继续接收新的样本。
算法输出N和C。图1为算法流程图。
1.2 SOINN算法的改进
原算法在获胜神经元邻居节点的权值更新过程中,将学习率固定为一个确定的较小值ε′(t)=1/100t,这样的设置不利于区分不同邻居节点与新输入样本的相似度,影响其学习效率。
1) 理论依据。在原始算法的神经元自适应调整过程中,通过神经元的相似度阈值T以及该神经元与输入节点的距离d来度量该神经元与输入节点是否属于同一个类别,并通过比较T与d的大小来决定进行类内插入还是类间插入。因此邻居节点的学习率ε′(t)应当与T、d具有一定的相关性,如图2所示,为输入样本,s1为获胜神经元,s2和s3为获胜神经元的邻居节点,s2与s3的学习步长应当与两者的相似度阈值T2、T3以及s1、s2、s3与输入节点的距离d(ξ,s1)、d(ξ,s2)、d(ξ,s3)相关。ε′(t)的设置要满足2个条件:① 获胜神经元与输入节点的距离始终小于邻居节点,因此两者的学习率要满足:ε′(t)<ε(t)。② 原始SOINN的约束条件为[12]:
改进SOINN的ε′(t)的设置也应当满足以上条件。因SOINN算法属于竞争学习的神经网络,且其神经元数量动态变化,因此算法在理论上无法进行严格的数学分析,文献[12]对此作出了阐释。

图1 单层SOINN算法流程

图2 SOINN算法类内节点插入及权重更新示意图
2) 算法步骤。提出一种动态的获胜神经元邻居节点学习率更新方式,即在原算法的第(6)步计算ε′(t)处进行改进。主要步骤为:
Step1:计算获胜神经元s1与新输入样本ξ的距离:
Step2:计算获胜神经元邻居节点i的相似度阈值Ti,计算该节点与新输入样本ξ的距离:
Ns1表示s1的所有邻居神经元。
Step3:比较Ti与d(ξ,i)的大小,如果d(ξ,i)>Ti,表示ξ与i的相似度较小,此时,学习率应当取较小值,按照原算法,取ε′(t)=1/θt,1/θ为学习率系数下限,通常情况下小于1/100。
Step4:如果d(ξ,i)≤Ti,且d(ξ,s1)≠0,表示ξ与i的相似度较大,此时根据ξ与获胜神经元及其邻居节点的距离来确定学习率,设学习率系数为τ1,即ε′(t)=τ1×1/t。
τ1的确定方法如下:

Step5:如果d(ξ,i)≤Ti,且d(ξ,s1)=0,表示ξ与s1重合,此时无法按照Step 4的方法来确定学习率,改为根据ξ与获胜神经元的邻居节点的距离来确定学习率,设学习率系数为τ2,即ε′(t)=τ2×1/t。
τ2的确定应当满足2个条件:①τ2与d(ξ,i)成反比关系,即随着d(ξ,i)的增大,τ2逐渐减少。② 两者的取值范围为d(ξ,i)∈(0,Ti),τ2∈[1/θ,1),当d(ξ,i)=Ti时,τ2=1/θ;当d(ξ,i)趋向于0时,τ2趋向于1。τ2的计算公式为:
Step6:更新获胜神经元邻居节点的权重
Wi=Wi+ε′(t)(ξ-Wi)
将改进后的算法命名为LRM-SOINN(SOINN with Learning Rate Modification)。
1.3 自动编码器
自动编码器可以自动从数据中学习特征,并尝试用低维特征来表征原始输入,是一种以重构输入样本为目标的无监督学习算法[15,16]。传统的自编码器模型是一种对称分布的3层网络结构,模型的Input层节点数量与Output层相同,在学习过程中,朝着尽可能重构输入样本的方向进行优化。图3为模型的基本结构。
自动编码器对输入样本x进行编码,从而获得新的低维特征h,期望通过h可以将输入x重构出来。编解码过程分别为:
h=f(x)
x′=g(h)=g(f(x))
重构误差L(x,x′)=L(x,g(f(x))),训练的目的是找到使得重构误差最小的神经网络参数,其中L是损失函数,惩罚x与x′的差距。如选择均方误差:

图3 自动编码器网络结构
2 基于增量自编码器的在线检测模型构建
2.1 增量自动编码器构建
自动编码器将重构误差作为损失函数来优化网络参数,从而学习到正常样本数据中的内存联系。进行异常检测的原理是计算测试样本的重构误差与正常行为模式的偏离程度,当其大于一定的阈值时,则被确定为异常。在训练自动编码器检测模型时,往往假设正常流量数据规模远大于异常,且异常样本对模型的影响非常小,只使用正常流量数据来训练网络。然而在现实环境下,网络空间中存在一定规模的异常数据,神经网络会学习到这些数据的规律,从而造成过拟合。异常数据的某些特征与主流样本的规律不同,但是量很小,利用这一特性,采用在输入层和隐藏层加入dropout层的方法来随机地忽略输入层节点,使得少量的异常数据获得学习的机会的概率进一步降低,使得这些数据对模型的影响变得更小。SOINN算法具有增量学习特性,在学习过程中可以保存已经学过的知识,不用存储历史样本,可减少运算与存储开销。本文将改进后的SOINN与自动编码器相结合,设计增量自编码器,既保证了算法效率,又不需要在新增数据后重新训练模型,可以在添加新的网络数据后不断进行学习,在节约计算成本的基础上又满足了高精度的要求。
算法首先对包含有大量正常样本和少量异常样本的无标签数据进行预处理,然后输入改进后的SOINN进行训练,将输出的少量神经元作为自动编码器的输入,训练得到异常检测模型,最后计算测试样本的重构误差得分并比较,判定是否为异常,若为正常样本则继续输入神经网络进行增量学习。模型实现流程如图4所示。

图4 基于增量自编码器的网络异常行为检测算法流程
基于增量自编码器的网络异常行为检测算法如下:
算法:基于增量自编码器的网络异常检测算法


1:设置LRM-SOINN参数:λ,max_age。初始化神经元集合N和连接关系集合C
2:fori=1 tomdo
4: 计算获胜神经元的相似度阈值


8: 进行类内插入,在2个获胜神经元之间增加一条边,并将年龄设置为0
9: 更新与获胜神经元相连边的年龄参数,如果年龄参数大于max_age,则删除该边
10: 更新获胜神经元及其邻居节点的权重
11: if 接收样本数量整除λ
12: 执行去噪操作
13:end for
14:ruturn神经元集合N、连接关系集合C
15:初始化自动编码器参数,将得到的神经元集合作为自动编码器的训练集
16:repeat
18: 采用Adma优化器优化损失函数,反向更新编码器和解码器的参数
19:until 损失函数收敛,得到编码器和解码器的参数
20:确定异常阈值δ
21:fori=1 tondo
23: ifScore(i)>δ

25: else

27: 输入LRM-SOINN进行增量学习
28: end if
29:end for
2.2 基于距离度量的样本标签筛选机制
测试集通过自动编码器进行预测,得到的正常样本中会包含少量的异常样本,基于距离度量的样本标签筛选机制就是要去除这些样本中的异常数据,使得反馈到LRM-SOINN网络中的正常样本纯度更高,接近99.99%。
LRM-SOINN的输出神经元作为正常样本的代表点,继承了正常样本的总体特征,分析SOINN算法可知,样本到神经元的距离可以度量两者之间的相似性。基于此,设计一种基于距离度量的样本标签筛选机制。首先计算自动编码器模型预测结果为正常的样本到LRM-SOINN输出神经元的距离,并选择最近的距离作为该样本的相似度值;然后对每一个样本的相似度值按照从小到大进行排序;最后设定样本筛选比例,将所选的样本作为增量学习的正常样本。图5为该方法的应用流程。
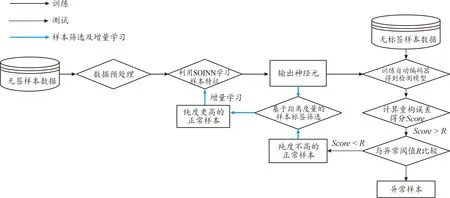
图5 基于距离度量的样本标签筛选机制应用流程
基于距离度量的样本标签筛选机制算法如下:
算法:基于距离度量的样本标签筛选机制算法
输入:LRM-SOINN的输出神经元集合U(Uj∈U,j=1,2,…,m),初始增量学习样本集Q(Qi∈Q,i=1,2,…,n)表示通过自动编码器模型后得到的正常样本集
输出:纯度较高的正常样本集Q′
1.fori=1 tondo
2.forj=1 tomdo
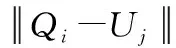
4.end for
6.end for
7. returnd=[d1,d2,…,dn]
8.采用冒泡排序法对d由小到大进行排序,得到d′=[d′1,d′2,…,d′n],根据索引得到对应的样本排序Q′=[Q′1,Q′2,…,Q′n]
9.确定样本筛选比例λ
10.得到正常样本集合Q′=[Q′1,Q′2,…,Q′t],t=|n×λ|
3 实验结果与分析
3.1 实验环境与数据集
在Win 10操作系统平台上利用Python 3.7.0开展实验,编程工具是PyCharm,处理器为Intel(R) Core(TM) i5-10210U,内存16 GB。实验数据为NSL-KDD数据集,表1显示了各类型数据的数量及所占比例。为更加贴近真实网络,本次实验中,训练集采用KDDTrain+中Normal样本和随机的5%攻击样本,测试集为KDD-Test+中的全部样本。

表1 NSL-KDD数据集样本分布情况
3.2 评价指标
在一次数据检测中,会产生TP(true positive)、FP(false positive)、TN(true negative,)和FN(false negative)4种检测结果。采用AUC值、准确率(Accurac)、召回率(Recall)、精确率(Precision)和F1-measure作为评价指标。AUC值是指ROC曲线下的面积,曲线的横、纵轴分别是FPR、TPR,表示预测的正例排在负例前面的概率,其值越高分类器性能越好。可用sklearn.metrics库中roc_curve和auc函数进行计算。其余指标的计算表达示为:
3.3 模型参数
网络结构及模型参数的选取对于自动编码器运行效果具有重要影响。经过多次对比实验,模型结构为[16,2,2,16]时,检测效果最好。损失函数描述了预测值与真实值的差距,通过得到的损失值来反向更新网络参数,使其逐渐收敛,Mean Squared Error (MSE)相比Mean Absolute Error (MAE)收敛更快。通过多次对比实验,LRM-SOINN的学习率极小值取1/150时,学习效果最好。基于上述实验与分析,模型的具体参数设置如表2所示。

表2 模型参数设置
3.4 检测性能
本部分实验主要验证改进SOINN与AE结合后形成的增量自编码器在检测性能方面的优势,实验分2部分内容。
3.4.1AE与其他模型的对比
为检验AE有异常检测中的性能优势,选择经典浅层机器学习算法PCA、OCSVM、孤立森林进行对比实验,ROC曲线如图6所示。从图6中可以看出,自动编码器对应的ROC曲线面积最大,AUC值为0.947 3,高于其他算法,表明AE较好地学习了样本特征,分类能力最好。

图6 ROC曲线对比
3.4.2增量自动编码器性能
为检验LRM-SOINN与自动编码器结合后的检测效果,对比实验分别为利用SOINN增量学习的AE和未进行增量学习的AE。ROC曲线如图7所示。LRM-soinn-Autoencoder的AUC值为0.936 0,紧次于Autoencoder,说明LRM-soinn在学习过程中丢失了少量的样本特征,但其依然继承了样本的多数特征。Soinn-Autoencoder的AUC值不如LRM-soinn-Autoencoder,说明改进后的算法提升了邻居节点学习效果,输出的神经元相比于SOINN更具代表性。

图7 ROC曲线对比
表3为不同算法对应的评价指标,均采用约登指数来选择最佳阈值,即为ROC曲线最靠近左上方的点对应的阈值。AUC值综合了不同阈值下模型的分类水平,评价更为客观。F1值为约登指数下选择的阈值对Recall和Precision的综合评价,更加依赖于阈值的选择。从表3中数据可以看出AE的AUC值最高,虽然OCSVM和Isolation Forest的AUC值比LRM-SOINN-AE高,但其F1值却很小,表明LRM-SOINN-AE的综合性能较好。

表3 不同模型异常检测实验结果
3.5 运算效率
本节主要研究改进后的SOINN算法与原算法相比,在时间和空间开销方面进行理论分析,并结合实验加以验证。
3.5.1时间开销
SOINN算法仅在查找获胜神经元的过程中采用了冒泡排序,其余过程均为线性计算,因此,总体复杂度为o(n)。改进后的SOINN增加了计算邻居神经元相似度阈值、邻居神经元与输入节点的距离以及学习率3部分内容,这3部分内容均为线性计算,因此,时间LRM-SOINN的时间复杂度也为o(n)。分别取输入样本数量为1 000~30 000进行实验,计算SOINN和LRM-SOINN的运算时间,实验结果如图8所示。由图8可知,随着数据规模的增长,运算时间呈现近似的线性增长趋势,与前述分析结果一致,增加了邻居神经元学习率修正的LRM-SOINN略高于原始的SOINN,但这部分开销相比于整体开销,其影响效果甚微,证明了改进后的LRM-SOINN不会增加太多的运算开销。

图8 算法运行时间对比图
3.5.2空间开销
为验证SOINN、LRM-SOINN的数据压缩特性,选取 1 000~50 000的样本规模进行实验,结果如图9所示。其中横轴代表样本规模,纵轴代表存储开销,也就是神经网络输出的神经元数量。由图9可知,对AE进行模型更新时,需存储所有已经训练过的样本,而利用SOINN和LRM-SOINN进行增量学习时,只需存储少数的输出神经元。

图9 算法存储开销对比图
3.6 增量学习能力
不同于离线学习的批量训练,增量学习在更新模型时,只需要用新的训练数据来训练模型,减少了模型更新的时间。为验证模型的增量学习能力,首先用初始训练集来训练初始模型,然后不断增加训练样本数,观察模型的性能变化情况。根据图10来划分实验数据集。其中初始训练集为30个正常样本,每一个增量训练集规模为50,增量训练次数为200次,测试集为KDD CUP测试集中包含正反例的所有样本。

图10 实验数据集划分
图11分别为AUC值随着数据规模增长的变化情况,为清楚比较2种算法的性能,图11(b)取前60次增量训练进行比较。由图12可知,随着训练数据的不断增加,AUC呈现波动上升趋势,且在前几个学习周期内上升较快,表明模型具备增量学习能力且学习能力较强。LRM-SOINN的性能指标曲线大多在SOINN之上,通过计算得知,模型训练稳定后,LRM-SOINN的AUC平均值为0.923 2,SOINN的AUC平均值为0.910 5,表明LRM-SOINN的总体性能要优于SOINN。

图11 AUC值随着数据规模增长的变化情况
3.7 在线学习能力
3.7.1样本标记准确率比较
本实验的目的是证明初始增量学习样本集通过基于距离度量的样本标签筛选机制算法后,得到的样本集中正常样本比例是否显著提升。实验首先用已经训练好的增量自编码器来预测测试集,得到初始增量学习样本集,然后对该样本集进行筛选得到新的增量学习样本集,通过调节样本筛选比例,来比较筛选前后,正常样本所占比例的变化情况。这里选择曼哈顿距离作为距离度量方式。经计算,初始增量学习样本集中,正常样本的比例为94.74%,经过筛选后,样本纯度随筛选比例的变化如图12所示。由图可知,当筛选比例小于0.4时,正常样本纯度就已经接近100%,证明该方法可进行样本筛选。

图12 样本纯度变化情况
3.7.2距离度量方式对模型的影响
在机器学习任务中,选择合适的距离度量方法非常作用。假设在n维空间中的2个点p=(x1,x2,…,xn)和q=(y1,y2,…,yn),dxy表示两点间的距离。常用的距离计算方法有:
1) 欧氏距离(Euclidean)。欧氏距离也叫L2范数,是最常用且易于理解的一种距离度量方法计算公式为:
2) 曼哈顿距离(Manhattan)。曼哈顿距离也叫L1范数,它描述的是两点在坐标轴上的投影距离之和,计算公式为:
3) 切比雪夫距离(Chebyshev)。切比雪夫距离描述的是两点之间各个维度坐标差的最大值,计算公式为:
4) 余弦相似度(Cosine)。余弦相似度通过向量夹角的余弦值来衡量向量的相似度,计算公式为:
为进一步确定不同距离度量方法对样本筛选的影响,对多种距离度量方法进行对比实验,实验选择筛选比例为 0.6~0.9,实验结果如图13所示。由图可知,采用余弦相似度的距离度量方式得到的正常样本纯度更高,其次为曼哈顿距离。但由于余弦相似度计算量较大,耗时更长,考虑算法用来进行在线检测,实时性要求更高。综合考虑,采用曼哈顿距离度量方法更为合适。

图13 距离度量方法对样本纯度的影响
3.7.3模型在线学习能力
为验证模型的在线学习能力,先取训练集中1 000个正常样本来训练初始模型,然后利用所有的测试集进行异常检测和增量学习。训练周期K代表每检测完K个样本后进行一次增量更新,∞代表不进行增量学习,直接进行测试,实验记录了随着训练周期的改变,模型检测能力变化情况,取值为所有训练周期内各评价指标的算术平均值,筛选比例设置为0.5,结果如表4所示。分析可知,随着增量学习周期的缩短,模型整体性能有所提升,表明了提出的增量自编码器模型具备一定的在线学习能力,当训练周期小于500时,AUC值达到了0.9以上,表明模型具备良好的分类性能。

表4 模型在线学习性能对比
4 结论
本文将SOINN算法进行了改进,提出具有更强学习能力的LRM-SOINN,通过与自编码器相结合,构建形成增量自编码器,通过基于距离的样本标签筛选机制来对测试集进行二次识别,使得反馈到模型中的正常样本纯度更高,模型在节约计算成本的基础上又保持了较高的检测精度。从检测性能、运算效率、增量学习能力和在线学习能力四个方面开展实验研究与分析,有力证明了方法的可行性和有效性。后续研究中,将结合科研项目验证模型在真实网络环境下的检测效能,提升其实用价值。
