基于交叉定位的声纳浮标阵被动检测预处理研究
2023-05-31王学敏李文海张翔宇
王学敏,李文海,张翔宇,2
(1.海军航空大学, 山东 烟台 264001;2.中北大学, 太原 030023)
0 引言
随着新型隐身技术在水下潜航器中的应用,水下潜航器辐射噪声随之降低,对传统声纳被动检测方法带来严峻的挑战。Hough变换检测前跟踪(hough transform track-before-detect,HT-TBD)技术在临界空间超高音速导弹、水下潜艇等低可探测性目标主动检测中得到了广泛研究及应用[1-3]。在探测水下目标时,HT-TBD算法可以直接利用单枚主动声纳量测的位置信息进行目标检测[4],但是HT-TBD算法通常无法直接利用被动声纳获取方位信息进行目标检测,而是基于多枚被动声纳采用交叉定位技术[2]获取量测的位置信息来检测目标,即检测前需要对量测点进行预处理。文献[5]指出预处理后的量测位置与被动声纳测向误差、交叉定位方法选取、浮标检测组选择有关,但未对其进行充分讨论,同时多目标、高噪声密度均会影响预处理的结果。
考虑数据关联是改善高噪声密度条件下多目标交叉定位的有效方法,因此在预处理阶段加入数据关联,有利于后续检测阶段HT-TBD算法性能的改善。传统数据关联算法主要包括:最近邻数据关联算法(near neighbor data association,NNDA)[6]、多假设跟踪数据关联算法(multiple hypothesis tracking data association,MHTDA)[7]、概率数据关联算法(probability data association,PDA)[8]等。其中,NNDA通常只能用于稀疏目标、低噪声的情况;采用PDA可以用于解决复杂噪声环境中数据关联问题,但仍未摆脱稀疏目标的局限,其改进算法概率数据关联算法(joint probability data association,JPDA)[9]能较好地解决复杂环境下的多目标数据关联,但其正确关联概率取决于联合事件与关联事件的概率,并且算法的实时性受目标数量和噪声密度影响较大。针对后验概率难以确定的问题,SHI、HUE等人分别在文献[10]和[11]中提出了基于粒子滤波的数据关联算法(particle filter data association,PFDA),借助粒子滤波的优势,扩展了数据关联的使用范围,但其不可避免的受限于粒子滤波自身算法的不足。SATAPATHI等[12]借助模糊集在处理不确定性问题思路,提出了基于模糊聚类的数据关联算法(fuzzy relational data association,FRDA)。FRDA适用于多目标数据互联,且具有较好的正确关联概率和实时性,但在噪声密度较大时性能会下降。
针对上述问题,本文中对被动浮标声纳测向误差、交叉定位方法、浮标检测组对定位精度影响展开研究,提出了一种基于最小交叉定位方差的距离和方位数据互联算法。
1 水下目标运动模型
水下目标在海上执行作战任务时,通常采用随机线性运动和随机曲线运动相结合的运动方式,以确保其水下航行的安全及隐蔽性。不失一般性,给出了线性和非线性2种运动系统模型。假定水下目标在二维平面内运动。此时,目标的时域离散系统模型为
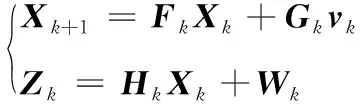
(1)
式中:Xk为状态向量;Zk为量测向量;Fk为状态转移矩阵;Gk为过程噪声分布矩阵;vk为过程噪声向量;Hk为量测矩阵;Wk为满足高斯特性的量测噪声向量。其中,k=1,2,…,K,K为量测时间,这里假定过程噪声序列、量测噪声序列及目标初始状态相互独立。
(2)
考虑过程噪声一般为高斯白噪声,过程噪声分布矩阵为
(3)
协方差矩阵为
Qk=E[Gkvk·(Gkvk)T]=
(4)
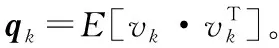
(5)
过程噪声分布矩阵
(6)
协方差矩阵为
Qk=E[Gkvk·(Gkvk)T]=
(7)
对于上述2种情况,量测向量为Zk=[xk,yk],对应的量测矩阵分别为
(8)
(9)
2 声纳浮标阵被动检测模型
在HT-TBD算法检测水下目标过程中,声纳测角误差是影响被动检测主要因素,而交叉定位方法和检测阵型选取也是影响被动检测重要因素。
针对不同作战需求,选择合适的声纳浮标阵型,可以有效提高检测。例如,对未知海区进行预警侦察时,通常采用覆盖阵;对于已知目标先验信息对其进行拦截侦察时,通常采用线型阵。在线形拦截阵中,通常采用两枚浮标构建浮标检测组对目标进行交叉定位处理;而在检查覆盖阵中,既可以构建2枚浮标检测组,也可以采用3枚浮标构建检测组。在直角坐标系中,声纳浮标线形阵和覆盖阵布设分别如图1(a)、图1(b)所示。

图1 声纳浮标阵型示意图
2.1 声纳浮标检测组
不失一般性,以声纳浮标面阵为例进行分析,线阵可看作面阵的特例。假设声纳浮标面阵由N行M列被动声纳浮标组成,其中,相邻行声纳浮标间距为D,相同行相邻浮标间距为d。在笛卡尔坐标系xOy中,声纳浮标位置坐标为(xsi,ysi)(i=1,2,…,NM),k时刻第i枚声纳浮标量测数据集合为
Zi={zki|k=1,2,…,K}
(10)
式中,zki={(θk(i)j,ek(i)j)|j=1,2,…,nj}为k时刻第i枚声纳浮标接收数据集。其中,nj为量测数目,θk(i)j为第j个测量的方位角,ek(i)jZ为第j个测量的能量信息,各浮标声纳间测量相互独立,方位角量测误差服从零均值高斯分布。
考虑单枚被动声纳浮标探测范围是有限的,针对水下目标低速运动特点,采用自适应关联方法,自动切换至检测效果最佳的被动声纳浮标,实现检测连续性和鲁棒性。即在被动声纳浮标阵的作用范围内,通过检测各浮标获取的信号强度,根据信号强度最大值来确定用于检测的3枚被动声纳浮标。
根据k时刻N枚被动声纳浮标接收方位角θk(i)j(i=1,2,…,N),表征其能量信息ek(i)j为

(11)
采用最大值法,得到能量值最大时对应的浮标i*,将其作为第1枚检测浮标。

(12)

2.2 交叉定位原理
以三声纳浮标检测组为例说明交叉定位原理[13-15]。在笛卡尔坐标系xOy中,假设3枚浮标布设位置坐标满足等腰三角形,k时刻sa、sb、sc3枚浮标对同一量测点的方位线分别为lak、lbk、lck,以正北方向为基准,对应的方位角分别为θak、θbk、θck。3浮标检测组交叉定位示意图如图2所示。
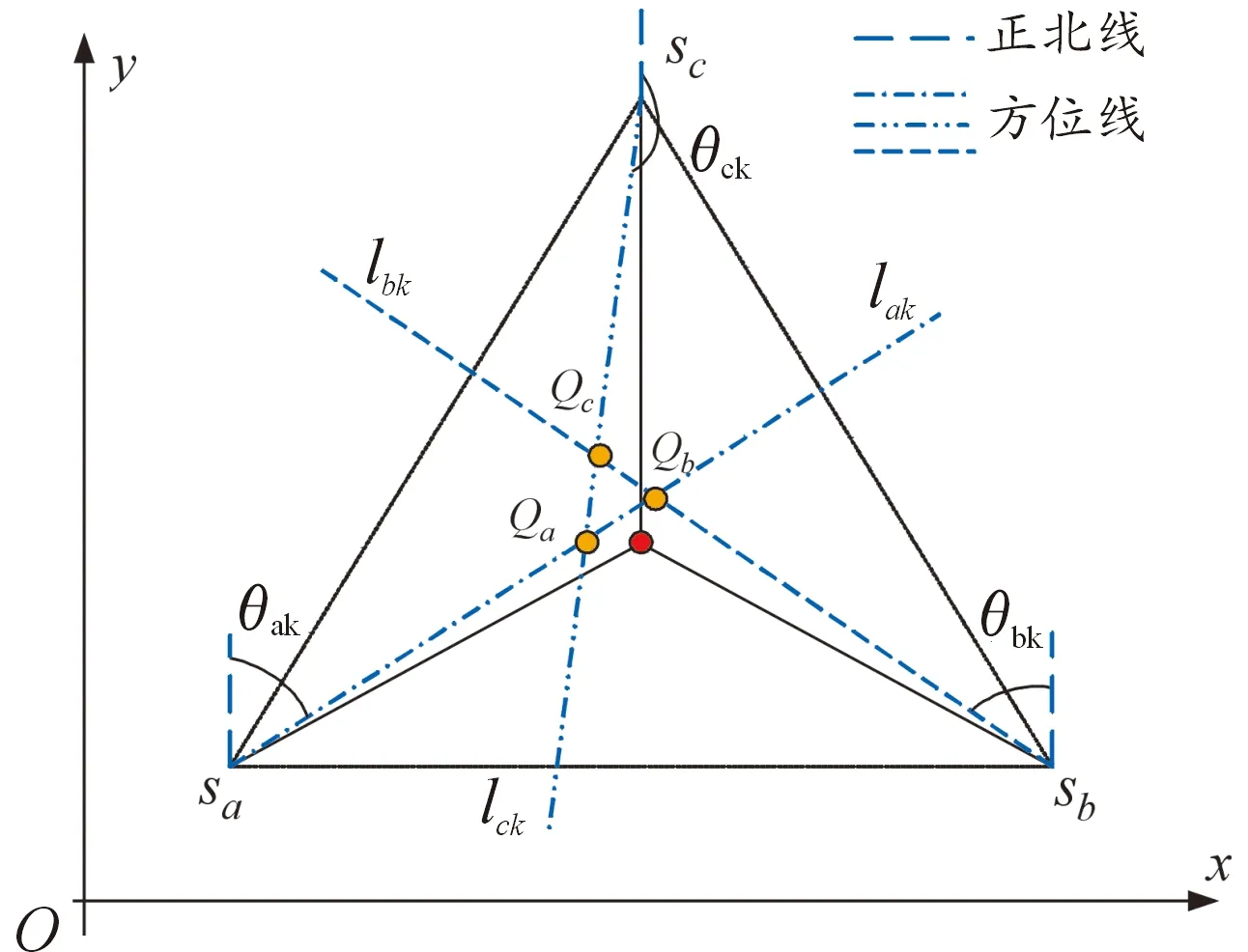
图2 3浮标交叉定位示意图
考虑浮标声纳测角误差的存在,3条方位线交点不再集中于一点,而是分别交于3点Qa、Qb、Qc。在图2中,用黄色点表示交叉点,红色点表示真实量测点。交叉点Qa的位置坐标(xak,yak)为

(13)
交叉点Qb的位置坐标(xbk,ybk)为

(14)
交叉点Qc的位置坐标(xck,yck)为

(15)
式中,声纳浮标间坐标满足xsc=(xsa+xsb)/2,ysc=xsa+D,ysb=ysa,xsb=xsa+d。
2.3 最小定位误差方差分析
假设在飞机布放声纳的位置误差范围内,3枚浮标坐标位置可以近似满足等腰三角,如图2所示。根据三角函数和几何关系可知,浮标sa与交叉点Qa的距离为

(16)
将rac按泰勒级数展开并取一阶偏导[16],可得rac误差方差的近似表达式为

(17)
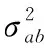
(18)
(19)
此外,浮标sb与交叉点Qb、Qc的距离和方差,浮标sc与交叉点Qa、Qc的距离和方差,参照上述求解。
浮标阵中用于检测的3枚声纳浮标对水下目标进行交叉定位,根据2.3节方差最小时对应2.2节位置坐标,作为目标的在直角坐标系中位置坐标。
3 基于最小方差交叉定位的数据互联算法
交叉定位误差直接决定了后续检测方法的性能,而多目标数据关联也是影响后续检测的重要因素。本文中选用3浮标检测组进行最小方差交叉定位,并对交叉定位后的量测进行距离和角度数据关联。具体算法流程如图3所示。此外,3浮标检测组对信号量测可能存在漏检,通过内插外推方法[17-18],改善量测漏检情况发生。
3.1 算法步骤
在声纳检测组探测区域内,假设目标和噪声的个数为N1、方位线与量测点一一对应。
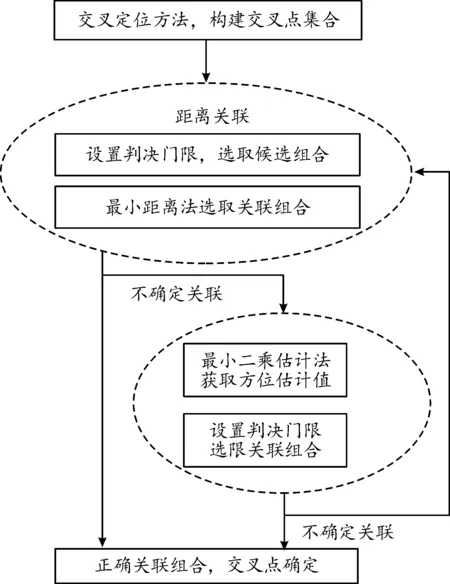
图3 算法流程
步骤1:采用2.3节最小定位误差方差分析,分别计算浮标sa与浮标sb、浮标sc的交叉点Qa和Qb,并按照方位线Lai(i=1,2,…,La)的顺序构建交叉点集合Aac={Qai=(xaci,yaci)}、Aab={Qbi=(xabi,yabi)},其中,La为声纳浮标sa方位线的条数且满足La=N1,Lai为声纳浮标sa第i条方位线。同时,构建方位线Lai对应的候选组合Bi=(i,g,j)(i,g,j=1,2,…,N1),其中,i、g、j分别为浮标sa、浮标sb、浮标sc对应的方位线序号。
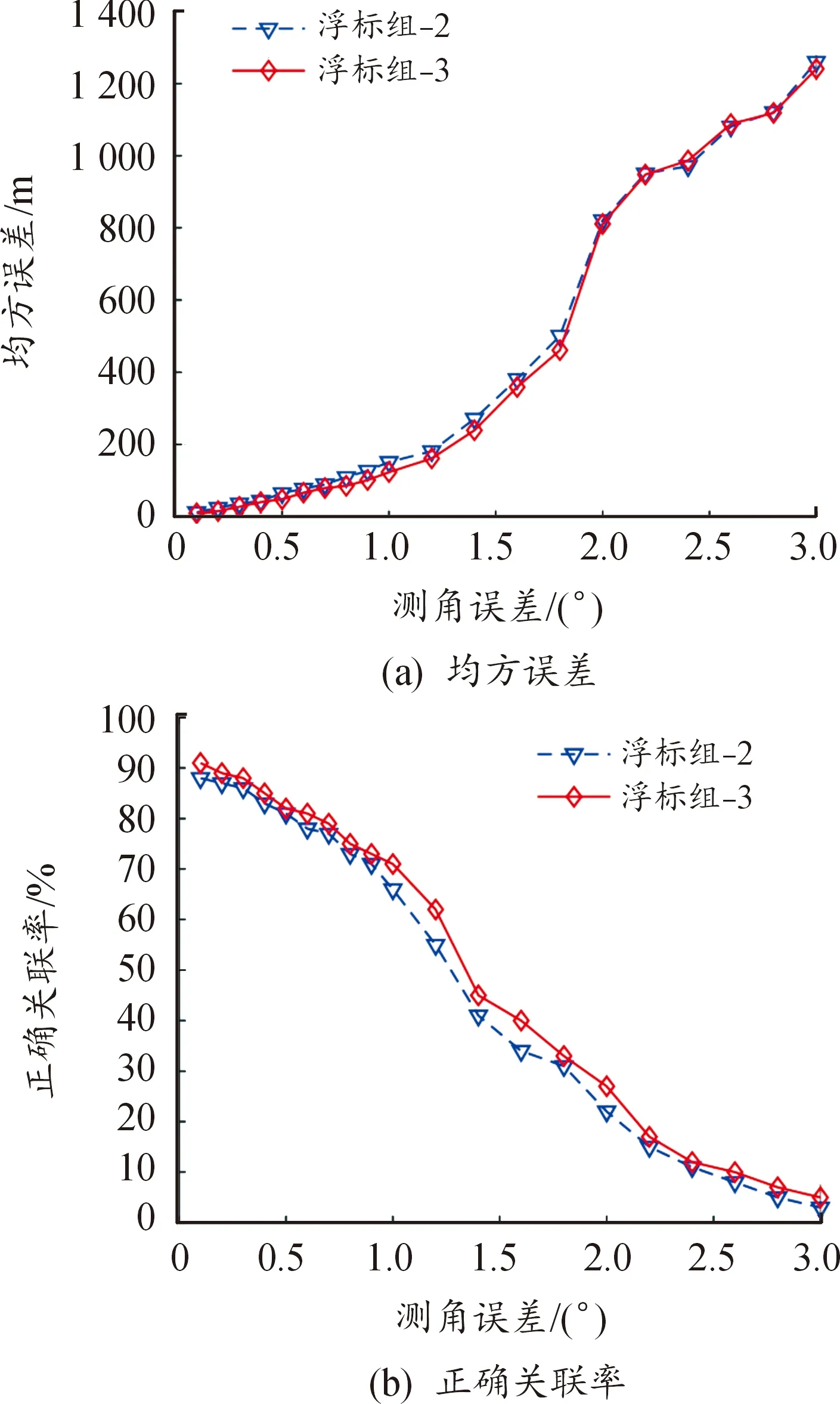
步骤2:设置判决门限G,计算交叉点集合Aac、Aab间的几何距离Dbc=|Aab-Aac|。当Dbc 在上述步骤中,关键是求解关联判决门限,3.2节将对此展开详细论述。 由2.3节定位误差分析可知,则有 (20) 当3条方位线来自同一量测时,根据准则3-σ[21],则有 (21) 本文中以Rab、Rca、Rbc最大值为距离检测统计量 Rabc=max{Rab,Rca,Rbc} (22) 距离关联判决门限可表示为 (23) 式中, 在3.1节步骤5中,计算目标位置估计X相对于浮标组si(xsi,ysi)(i=a,b,c)的方位估计为 (24) 根据式(24),构建满足χ2分布的方位检测统计量为 (25) 其中,σθi和θi分别为声纳浮标si的测向标准差和实际测量值。 根据自由度n和显著性水平a查χ2分布表,得到门限λa(n),作为方位关联判决门限。 声纳浮标检测组由3枚浮标组成,对应位置为(6.3 km,5.7 km),(9.3 km,1.1 km)、(12.3 km,5.7 km),作用距离为5 km,测角误差为不大于3°,误差类型为零均值高斯噪声;假设在声纳浮标阵共同探测范围内存在3个目标,目标1~目标3的初始位置分别为(8.0 km,7.0 km)、(9.5 km,7.0 km)、(8.5 km,7.0 km),初始航向均为60 °(正北为0°,逆时针为正),航速平均值为10 m/s;信噪比取5 dB;设噪声密度λ为以浮标作用距离为半径的圆形区域内含有噪声数,取λ=100;以水下目标实测辐射噪声数据为基础对本文中算法的数据关联性能进行仿真研究;Monte Carlo仿真试验次数为100次,以平均值作为最终的检测性能指标。 浮标组接收信号经过交叉定位预处理后的量测位置信息中存在交叉定位误差,直接影响后续检测的效果。交叉定位距离误差与浮标测角误差、浮标组选取密切相关。根据2.3节浮标与交叉点的距离公式计算不同测角误差所对应的交叉定位距离均方误差[21]。根据3.2节距离关联判决门限Gabc和方位关联判决门限λa(n)确定关联概率。正确关联概率等于正确关联次数与总关联次数比值。 采用4.1节参数设置进行仿真实验。图4给出了含2枚浮标组和含3枚浮标组(分别用浮标组-2和浮标组-3表示)在不同测角误差条件下交叉定位距离均方误差及正确关联率。 图4 不同浮标组条件下的关联 由图4看出,随着测角误差增加,基于两类浮标组的交叉定位均方误差均随之增加。而采用浮标组-3对应的定位精度整体上优于采用浮标组-2对应的定位精度。这是因为采用3枚浮标交叉定位,可以选取最小方差的浮标组合进行交叉定位,从而改善定位精度。这也是浮标组-3的正确关联率优于浮标组-2的原因。当测角误差不超过1°时,浮标组-3对航向相同的3个水下目标的正确关联率可到70%以上。因此,在实际探测过程中,应充分利用多枚浮标阵来改善正确关联率。 为了进一步验证算法的性能,分析浮标间距对本文中算法的正确关联率影响。改变浮标间距,浮标位置也随着改变,为保证合理的正确关联概率,根据4.2节分析,取测角误差为1°,其他参数设置与4.1节一致。表1给出了不同目标数条件下的正确关联情况。 表1 不同目标数条件下的正确关联情况 由表1可以看出,在声纳浮标组有效探测范围内和相同的噪声密度条件下,目标4种组合的正确关联率都随着浮标间隔的增大得到改善。并且目标间隔变大,正确关联概率也随之提高。这是因为随着浮标之间距离的增加,交叉定位精度随之提高,多目标的正确关联概率也得到提升。因此,在声纳浮标组有效探测范围内和相同噪声密度条件下,浮标阵应尽量采用较大距离间隔。 为了进一步验证本文中算法的性能,以正北为0°,将目标1~目标3的初始航向分别调整为30°,45°,90°,其他参数设置参照4.3节,图5(a)给出了目标航迹示意图。在目标航迹交叉条件下,将本文中算法与最邻域法[22]、模糊聚类法[23]进行对比分析。图5(b)、图5(c)分别给出了3种算法在不同测角精度条件下的数据关联正确率和平均运算时间。 由图5(b)可知:随着测角精度的降低,3种算法的正确关联率逐渐变差。本文中算法和模糊聚类法的正确关联率均优于最邻域法,且本文中算法性能趋近于模糊聚类法。当测角精度不大于0.5°时,在目标航迹交叉条件下,本文中算法的正确关联率可以达到65%以上。这是因为多目标会导致最近邻域法对漏检、误检和虚检的观测结果比较敏感,而采用距离和方位两级关联处理,本文中算法要比最邻域法单一的距离关联处理更精细。随着测角误差增大,模糊聚类法中的某一类的隶属度值不确定性,正确关联率随之变差。 由图5(c)可知:3种方法的平均单次运算时间是随着测角精度的增加而增加。其中,模糊聚类法实时性最佳,最近邻域法耗时最多,而本文中算法的计算时间介于两者之间。这是因为为了有效的获取确定关联组,本文中算法要对不确定关联进行再次确认,增加了运算时间。 为了进一步验证算法的有效性,在噪声密度取λ=200条件下,对3种算法的性能作进一步分析。图6给出了λ=200三种算法的数据关联正确率和平均运算时间。 由图6可以得知:随着噪声密度增加,3种算法的正确关联率变差,且平均耗时增加。这是因为模糊聚类法的正确关联能力和实时性对噪声密度变化最为敏感,这也与文献[24]中的分析是相一致的。 综上分析可知,在多目标航迹交叉、复杂噪声环境条件下,本文中算法性能整体上要优于最近邻域法和模糊聚类法。 图5 不同算法性能分析 图6 λ=200时三种算法性能分析 为了改善HT-TBD算法在水下多目标被动检测中的可靠性和有效性,提出了一种基于最小交叉定位方差的水下目标数据关联算法。仿真结果表明: 1) 该算法的正确关联率与声纳浮标测角精度成正相关,同时浮标检测组含有浮标数目、浮标相邻间距以及目标间距也是影响正确关联概率重要因素。 2) 在测角误差小于1°条件下,具有较好的关联性能。尤其在复杂噪声环境、多目标航迹交叉条件下,整体性能优于现有部分数据关联方法。而在测角误差较大情况下关联算法性能提升及实际运用是下一步研究方向。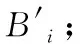


3.2 关联判决门限



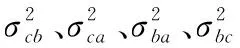
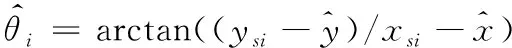
4 仿真验证
4.1 参数设置
4.2 浮标组类型对算法性能影响
4.3 浮标间距对算法性能的影响

4.4 不同算法性能分析


5 结论
