轮腿式无人战车越障性能分析

许志伟,朱纪洪

(1.广西大学 机械工程学院, 南宁 530000; 2.清华大学 精密仪器系, 北京 100084)

0 引言

无人战车指的是在陆地上完成特殊任务的机器人,是机械、信息、电子与人工智能一体化的作战平台[1]。传统的无人战车平台可分为轮式、腿式和履带式[2]。轮腿式无人战车因其独特的轮腿结构,可在复杂的地形中进行轮腿复合越障,通过性强,能够在军事行动、救援抢险中发挥着重要的作用。为了能够在复杂的地形中工作,需要战车具有良好的环境适应性,其中越障性能是评价无人战车性能的关键参数,因此需要对无人战车的越障过程进行分析。

国内外许多科研人员提出了能够适应复杂地形的轮腿式行走车辆。Kerrbrat[3]提出了6轮全驱动纵臂悬挂式无人战车,通过悬挂的协同控制,可完成高于轮胎直径的越障,但未对越障过程进行分析。王超星、贺继林等[4-5]针对全地形移动平台进行垂直墙全过程动力学越障分析,可适应不同高度的垂直墙障碍,但其具有复杂越障机构的轮腿式机器人研究局限于微型移动平台[6-7],在军事运输、抢险救灾[8-10]等情况下都不能满足承载能力的需求。“Guardium”[11]车辆具有双横臂悬架的优点,机动性强,拥有35%自重有效载荷,但越障能力有限。Zhou[12-13]提出了一种马启发全地形8轮与4摆动臂车辆,具有良好的越障性能。

在相关研究的基础上,本文提出了一种全液压驱动的轮腿式无人战车,通过8摆臂的协同控制,调整车身姿态,以适应于军事行动、抢险救援工作的需求。首先分析轮腿式战车的结构,从动力学以及姿态规划来分析战车的越障性能,求出越障高度与摆角的关系以及极限越障高度,并对不同越障高度下进行步态规划,利用QT、Simulink、ADAMS构建综合仿真平台,对无人战车越障全过程进行仿真验证,为轮腿式无人战车的后续优化以及通过复杂地形的实验测试提供理论依据,满足复杂地形的抢险救灾的特殊需求。

1 8轮全驱动轮腿式战车构型设计

1.1 油缸摆动臂设计原理

轮腿式无人车的液压摆臂结构如图1所示,O点为油缸固定铰支座点,B点为膝关节,A点为摆臂铰支点,C为轮心,OB为可伸缩的悬架油缸,AC为摆动臂,OA为油缸固定铰支座到摆动臂的距离。其工作原理为悬架油缸OB改变其伸长量,通过关节B的牵连摆动以及A点的转动,从而实现车轮的离地调节。β为AC与沿着车身正向的夹角,即为摆臂摆角,δ2为AB与AC之间的夹角。摆臂主要参数如表1所示。

悬架油缸的行程Lh与δ1之间的关系为:

(1)

因此悬架油缸的行程Lh与摆臂摆角β之间的关系为:

(2)

(3)

其中悬架的长度Li与油缸行程的关系为:

Li=Lh-1 010.8

(4)

式中,i为不同摆臂对应的悬挂长度(i=1、2、3、4),悬架长度Li单位为mm。

以A点摆臂铰支点为原点建立直角坐标系,可得轮心的坐标为:

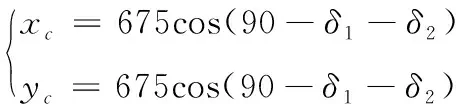
(5)

图1 油缸摆动臂

表1 油缸摆动臂结构参数

由式(1)、式(5)可求得车轮轮心的横纵坐标与液压缸行程的关系,如图2所示。

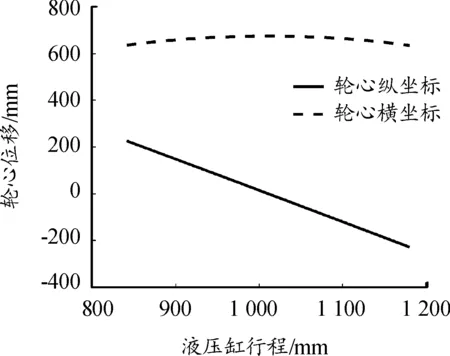
图2 轮心位移与液压缸行程

由图2可以看出,随着液压缸行程的减小,液压悬挂逐渐收起,车轮跟着逐渐离地状态,当液压行程最短时,轮心的纵坐标最大可达226.35 mm。因此,通过8轮摆臂的协同配合,无人战车可以完成不同高度的垂直墙越障。

1.2 8轮4轴轮腿式全驱动战车总体构型

在油缸摆动臂的基础上,8轮4轴全驱动轮腿式战车结构如图3所示,战车由车体、摆臂、底盘及动力总成、油气悬架组成,车轮通过轮毂电机进行驱动,轮腿机构通过油气悬架进行摆动,4为双向油缸和蓄能器的油气悬架,可以稳定调节车轮位置和车身姿态,通过电机控制油缸和蓄能器之间的开关阀,调整油路的流向,从而控制悬架带动车轮的收起或者伸长。当阀口打开时候,油缸的工作过程与油气悬架相似,使得无人战车具有良好的减震性能。同时,战车的轮腿布置采用前轮、中后轮导向式,中前轮、后轮采用拖拽式能够让战车有更大的接近角和离去角,使得平台通过性强,提高越障的性能,便于适应抢险救灾等复杂工作环境。无人战车的主要参数如表2所示。

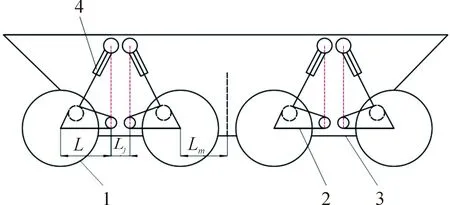
1.车轮; 2.摆臂; 3.底盘及动力总成; 4.油气悬架

表2 无人战车主要参数

2 8轮4轴轮腿式战车越障性能分析

2.1 越障过程分析及运动姿态初步规划

4轴轮腿式战车跨越垂直墙的过程如图4所示。为了便于进行理论分析,将摆臂机构和液压缸部分简化成连杆机构,越障的过程可以分为4个步态:步态1为前轮越障,从姿态调整到前轮完成越障,如图4(b)、图4(c)所示;步态2为中前轮越障,如图4(d)、图4(e)所示;步态3为中后轮越障,如图4(f)、图4(g)所示;步态4为后轮越障,如图4(h)、图4(i)所示。前轮、中前轮、中后轮、后轮分别对应一轴、二轴、三轴、四轴悬挂。

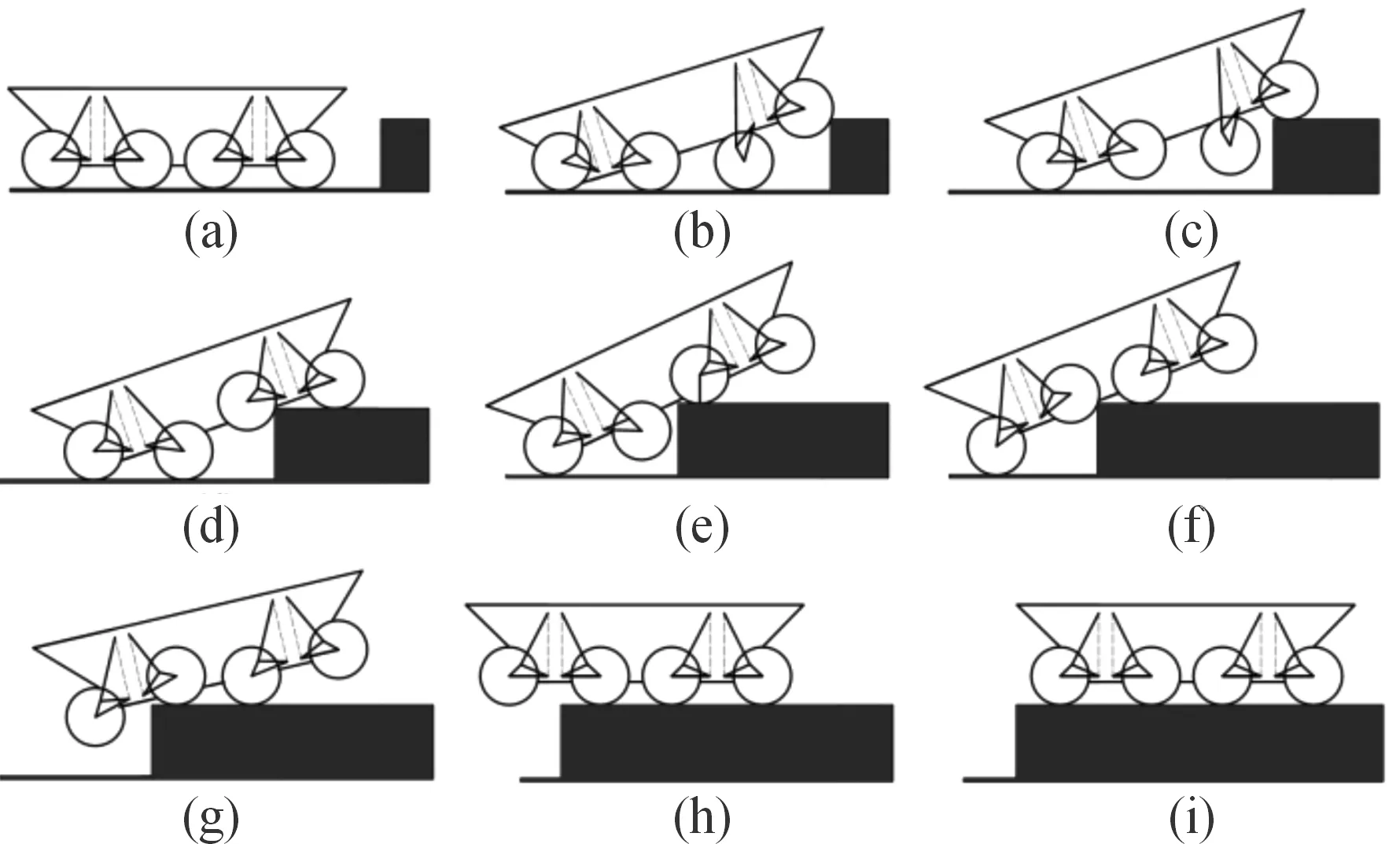
图4 垂直墙越障过程

2.2 越障性能分析

2.2.1前轮越障

前轮越障过程如图5所示,xm和ym分别是战车的质心世界坐标值。

图5 前轮越障过程

在下一时刻中前轮、中后轮会脱离地面,忽略轮胎特性引起的变形基于理论力学可得动力学方程为:

(6)

由几何关系可知,α与车身俯仰角θ之间的关系为:

(7)

其中:

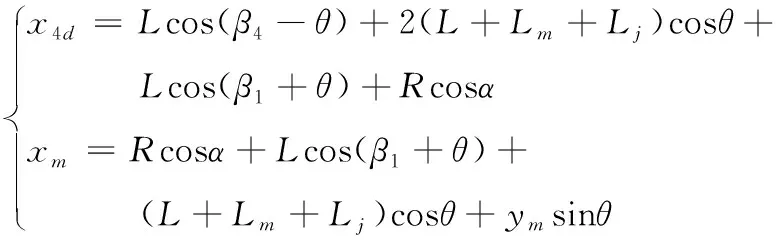
(8)

其中,二轴摆角、四轴摆角与俯仰角之间的关系对应的方程为:

(2L+2Lm+Lj)sinθ-Lsin(β4-θ)-

Lsin(θ-β2)=0

(9)

在越障过程中,假设以很低的速度进行平稳越障,忽略加速度的影响,因此,对式(6)—式(9)联立,可以求出在前轮越障过程中,四轴轮腿式战车的垂直墙高度与一、二、四轴摆臂摆角之间的关系式为:

H=-((μ2cosα+cosα)(G(Lcos(θ+β1)+

(L+Lj+Lm)cosθ+Rcosα+ymsinθ)-

(G(cosα-μsinα)(Lcos(θ+β1)+Rcosα+

(2L+2Lj+2Lm)cosθ+Lcos(θ-β4)))/

(μ2cosα+cosα)))/(μG(cosα-μsinα))

(10)

其中:

(11)

α=arcsin((Lsin(β1+θ)+R+

2(L+Lj+Lm)sinθ-Lsin(β4-θ)-H)/R)

(12)

对8轮4轴轮腿式战车跨越水泥台垂直障碍进行研究,水泥台附着系数约为0.7,俯仰角的变化在[0°,12°]。将战车参数信息代入式(10)中,通过调整摆臂摆角可以得到确定的可越垂直墙高度。

但是,式(10)—式(12)存在较多的三角函数非线性,在进行动力学计算过程会增加计算的复杂性,为了简化计算,将复杂的三角函数关系用regress多元线性回归拟合,对式(10)—式(12)进行求解,可得一、二、四轴摆臂摆角与障碍物高度之间的关系如式(13)所示,该公式可用于不同高度下无人车运动姿态规划的依据。其中,H的单位为m。

H=0.719 3β1-1.159 2β2+0.457 4β4+0.425 2

(13)

根据无人车的结构,在一轴摆臂轮越障中,车身俯仰角的变化与二轴摆臂、四轴摆臂摆角有关,当车身俯仰角θ=0°,即二轴、四轴液压悬挂都在中位,且一轴悬挂收至最短下,即β1=18.5°,理论上能通过的最低的垂直墙高度为657.4 mm,该高度不能满足无人车的越障指标,故当θ>0,为了减少越障过程中对一轴摆臂悬挂的冲击,因此始终让一轴悬挂收起最短,即对应的一轴摆臂摆角β1=18.5°,再对二轴摆臂伸长至极限位置,可进一步提高越障高度,最后对四轴缩短至极限位置,由此可得到一轴越障约束规划曲线,如图6所示,其中H(θ,μ)是由动力学方程所决定的路面附着条件,H(θ)是由俯仰角所决定的几何约束条件。

但是在实际应用中,我们是通过电机控制油压阀门,进而控制悬架油缸的长度,因此通过合理调整悬架油缸的长度,可以完成整个垂直墙越障过程。因此,将式(3)、式(4)代入化简,可得到垂直墙高度H与一、二、四轴悬挂长度的关系为:

H=0.452 7-3.054×10-4δ2-0.719 3×

(14)

式中:Lh1、Lh2、Lh3、Lh4分别为一、二、三、四轴悬挂长度变化量,悬挂伸长为正值,悬挂收起为负值。变化在[-170～170],单位为mm。

由式(14)可知,一轴越障主要由几何约束即二、四轴摆臂轮的悬挂长度有关,通过姿态的运动进行规划是前轮越障的主要因素,通过理论计算可越垂直墙最大高度为1 219.36 mm。

图6 一轴摆臂轮越障约束规划曲线

2.2.2中前摆臂轮越障

在下一时刻,前轮和中后轮随后会离地状态,因此在该过程的越障力学分析中无需考虑一、三轴摆臂轮的驱动作用。

在步态1前轮完成越障后,车身俯仰角会发生变化,通过式(15)可得到前轮完成越障后,不同垂直墙高度下对应的俯仰角变化后的角度θ,H0为此时步态1前轮越障对应的垂直墙高度。中前轮越障过程如图7所示。

H0=-Lsin(β4-θ)+Lsin(β1+θ)+

2(L+Lm+Lj)sinθ

(15)

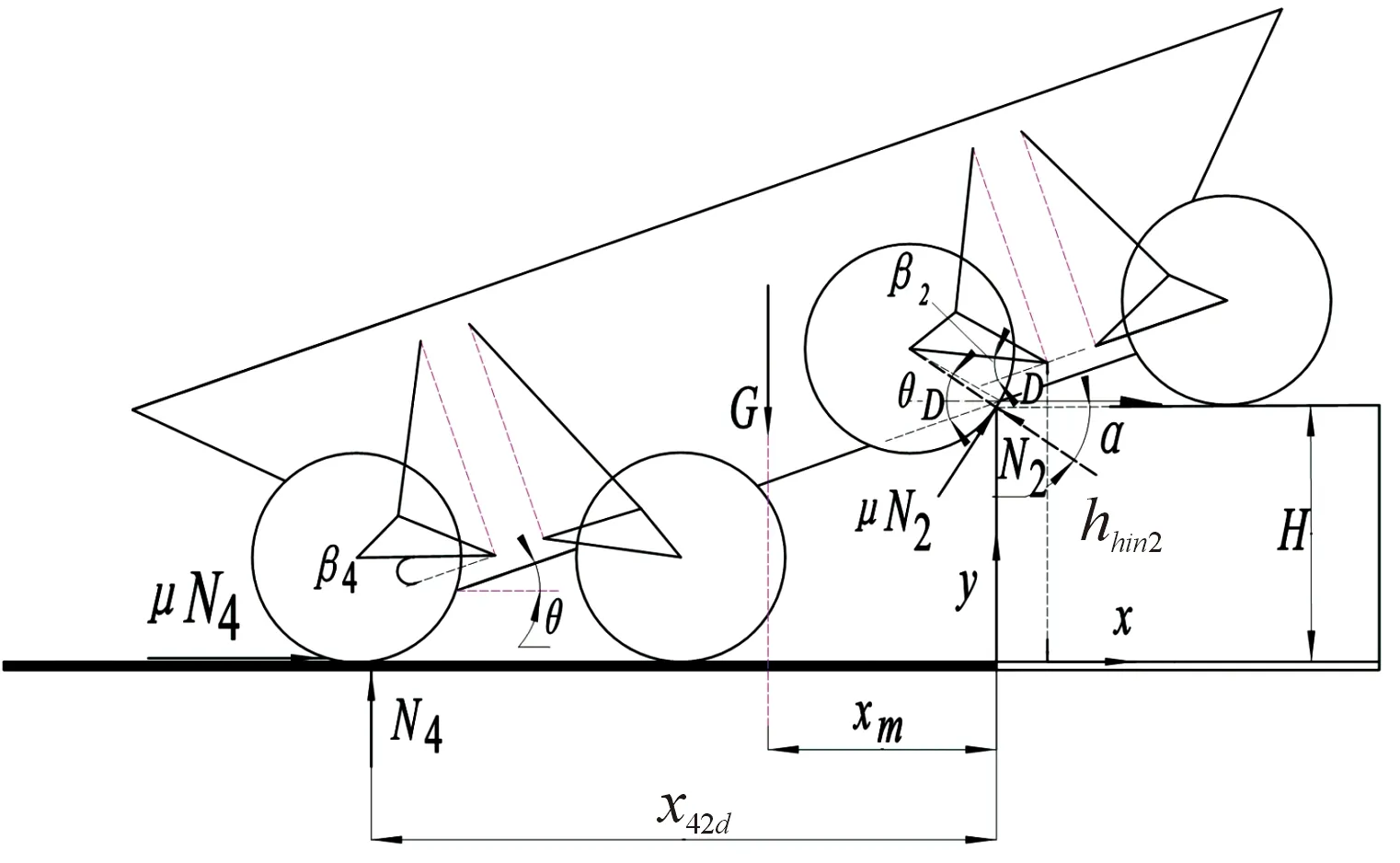
图7 中前轮越障过程

忽略轮胎特性的变形,可以得到中前轮越障动力学方程为:

(16)

其中:

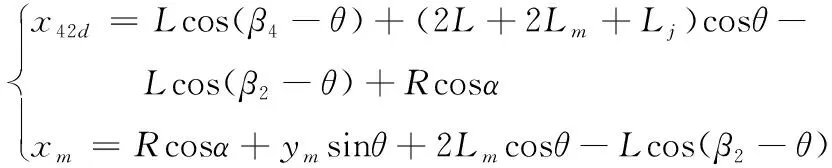
(17)

由二轴越障过程α与俯仰角θ的关系可得:

Rsinα=Lsin(θ-β4)+(2L+2Lm+Lj)sinθ-

Rsinα-Lsin(θ-β2)-H+R

(18)

因此可以求出:

H=-((μ2cosα+cosα)(G(cosθ(L+Lm)+

Rcosα-Lcos(θ-β2)+ymsinθ)-

(G(cosα-μsinα)(cosθ(2L+Lj+2Lm)+

Rcosα-Lcos(θ-β2)+Lcos(θ-β4)))/

(μ2cosα+cosα)))/(μG(cosα-μsinα)))

(19)

其中:

(20)

α=arcsin((R-Lsin(θ-β2)+Lsin(θ-β4)+

(2L+2Lm+Lj)sinθ-H)/R)

(21)

在该状态下,为了避免出现碰底盘的情况,需要保证底盘的高度要大于垂直墙高度,即:

H0≤hhin2+Lsin(β2-θ)-Rsin(θD-θ)

(22)

其中:

hhin2=R-Lsin(β4-θ)+(2L+2Lm+Lj)sinθ

(23)

(24)

根据无人车的结构,在中前轮越障中,在只调整收起二轴悬挂的长度可求出对应的可越垂直墙高度,再调整俯仰角的变化,即调整一、四轴悬挂长度可进一步提高可越垂直墙高度。由此可得到中前轮越障约束规划曲线,如图8所示。

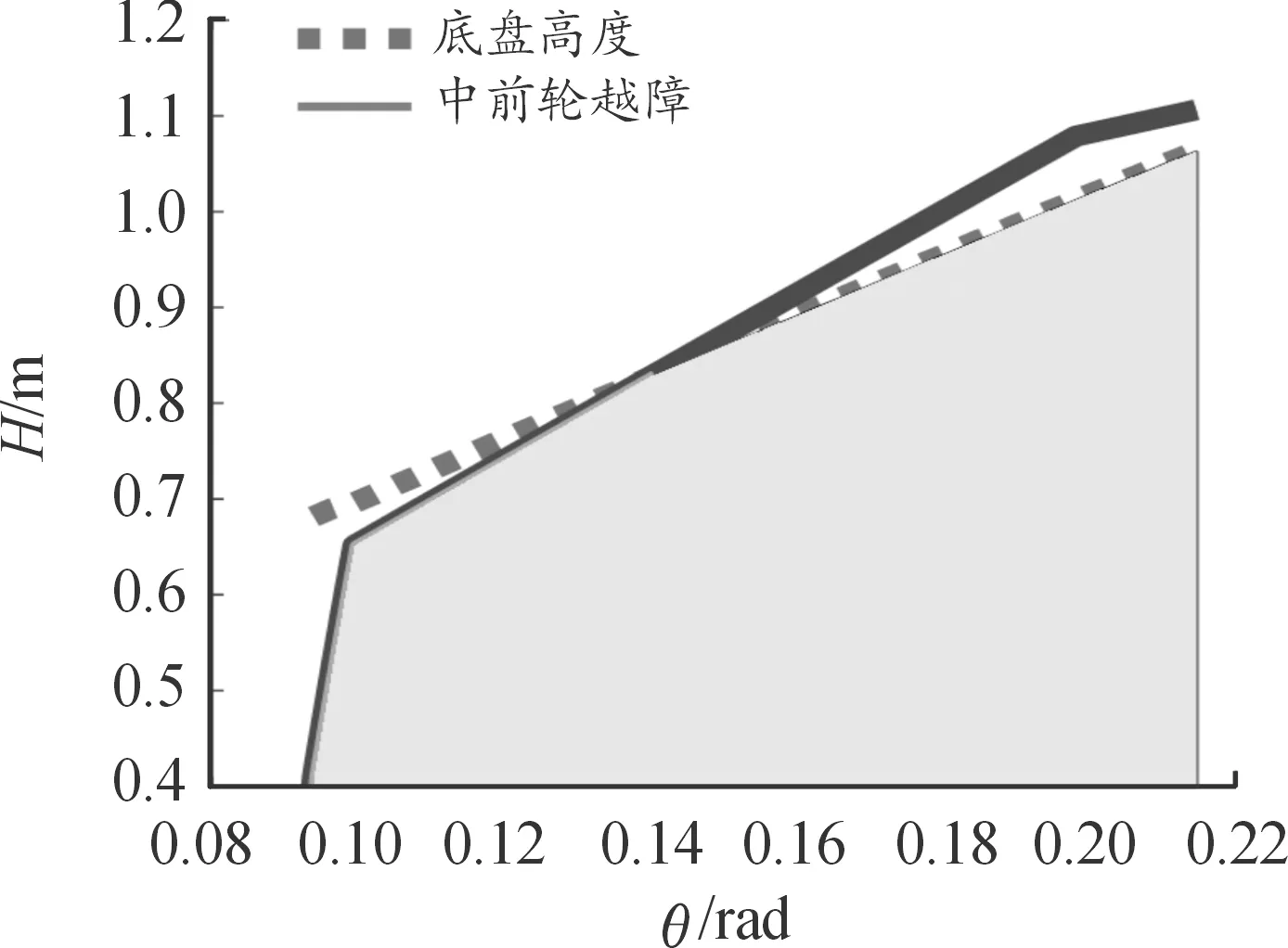
图8 二轴摆臂轮越障约束规划曲线

图8中,实线为中前轮越障时,在只调整收起二轴悬挂的长度对应的可越垂直墙高度,俯仰角的变化是由步态1前轮完成不同高度越障后所导致。在θ=0.104 6 rad,对应的可越垂直墙高度为673.9 mm,实线斜率发生变化是由于在此高度上,步态1的二轴悬挂的收起,从而影响了俯仰角的变化。虚线为底盘极限碰底点的高度,当可越垂直墙高度为819.8 mm时,θ=0.138 1,求得二轴悬挂摆臂的摆角为 0.226 016 rad,底盘极限碰底高度恰好与可越障高度相同,当可越垂直墙高度继续增大时候,即继续收起二轴悬挂的长度,底盘碰底高度低于垂直墙高度,会在一轴轴之间的底盘发生碰撞,从而导致中前轮越障的失败。

在中前轮越障中,为了避免发生碰底的情况,当垂直墙高度大于819.8 mm时候,将一轴悬挂伸长撑起至中位以提高车身俯仰角。

因此,基于式(19)—式(21)和上述分析可以求得一、二、四轴摆臂摆角与障碍物高度之间的关系如式(25)所示,式(25)可用于不同高度下无人车运动姿态规划的依据。

H=0.195-0.521β1+0.77β2-

0.205β4+0.758H0

(25)

式中:H0为步态1前轮越障对应的垂直墙高度;H为步态2中前轮越障中的可跨越的垂直墙高度。

将式(3)、式(4)代入式(25)中,可得到H与一、二、四轴悬挂长度的关系为:

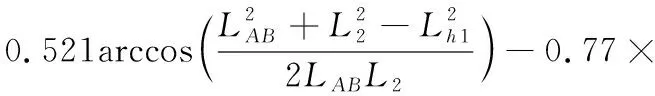
0.758H0+0.265-7.784×10-4δ2

(26)

根据式(26),通过数值计算结果可知:

1) 当垂直墙高度在520.8 mm以下时,中前轮越障过程无需姿态调整可完成垂直墙越障。

2) 中前轮越障中,将一轴悬挂伸至最长的情况下,理论上可越过最大垂直墙高度为1 599.7 mm,但是在该状态下,俯仰角为18.95°,不满足越障规范要求,容易在下一状态步态3的二、三轴摆臂轮之间发生碰底的情况,故为了保证俯仰角在合理的结构设计规范范围内,将一轴悬挂伸长回至中位可满足要求。

2.2.3中后轮越障

中后轮的越障过程如图9所示。由于下一时刻后摆臂轮会离开地面,因此在该越障过程中不用考虑前轮、后轮的驱动作用。

(27)

L2=2(L+Lm)cosθ-L(cos(β3+θ)+

cos(β2-θ))

(28)

α与H之间的关系为:

Rsinα=R-Lsin(β4-θ)+Ljsinθ+

Lsin(β3+θ)-H

(29)

根据垂直墙列出,俯仰角与二四轴摆角的关系为:

-Lsin(β4-θ)+(2L+2Lm+Lj)sinθ+

Lsin(β2-θ)-H0=0

(30)

图9 中后轮越障过程

在中后轮越障过程中,从运动学的角度进行分析,还应该满足战车的质心越过垂直墙的边沿线[14],因此在该过程中需要以四轴摆臂轮为原点建立如图9所示的坐标系,通过几何约束,可以得到H与质心坐标的关系为:

H=R+xGsinθ+yGcosθ-2Rsinα-

(31)

式中,xG、yG分别为无人战车的横、纵坐标。

由于车体的质量远大于轮腿摆臂的质量,轮腿的位姿变化对战车的重心位置影响很小,因此可认为战车的质心始终在车体中心。

因此联立式(27)—式(30)可以求得可越垂直墙高度与二轴、三轴、四轴悬挂摆角之间的关系为:

H=R-Lsin(β4-θ)+Ljsinθ+Lsin(β3+θ)-Rsinα

(32)

其中:

(33)

α=arcsin((G(xmcosθ-ymsinθ-

Lcos(β3+θ))-n2((2L+2Lm)cosθ-

L(cos(β3+θ)+cos(β2-θ)))-μRn3)/(μRn2))

(34)

N2=G(cosα-μsinα)/(μ2cosα+cosα)

(35)

N3=(μG)/(μ2cosα+cosα)

(36)

联立式(32)—式(36),可得到中后轮越障曲线如图10所示,通过数值仿真可以求得可越垂直墙高度与二轴、三轴、四轴悬挂摆角之间的关系为:

H=0.222-0.199 6β2+0.674 2β3-

0.277 9β4+0.492 6H0

(37)

在图10中,当垂直墙高度小于432.9 mm时,即俯仰角小于0.151 rad,中后轮无需调整姿态可完成越障。在只有三轴悬挂作用下,可越垂直墙最大高度为803.1 mm;为了进一步提高越障高度,当三轴悬挂收至最短,伸长二轴悬挂,可以提高垂直墙的越障高度,最大可越障1 022.9 mm;四轴悬挂的伸长作用,会减小车身的俯仰角,但会进一步提高可越障高度,四轴悬挂伸至最长时,战车最大可越障高度约为1 209.3 mm。

图10 三轴摆臂轮越障约束规划曲线

同样可以求得垂直墙高度与二、三、四轴悬挂之间的关系为:

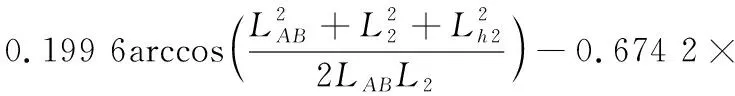
0.492 6H0+0.531 1-3.433×10-3δ2

(38)

综合以上的分析可知,轮腿式无人战车最大可通过的垂直墙高度为1 209.3 mm。

2.3 不同垂直墙高度下步态规划

根据前面的计算,越障可以分为4个步态:步态1调整姿态后进行前轮越障,其中三轴摆臂轮通过开减震模式伸长作配合作用;步态2为中前轮越障,三轴摆臂轮作配合作用;步态3为中后轮越障,一轴摆臂轮作配合作用;步态4为后轮越障。由此可以得到不同垂直墙高度下不同的越障策略,H代表的是垂直墙的高度。

步态1:H<0.425 2 m无需调整姿态直接完成越障。

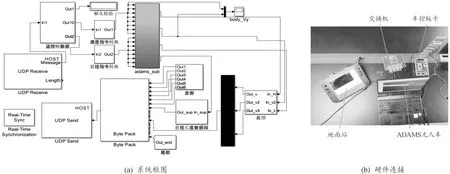
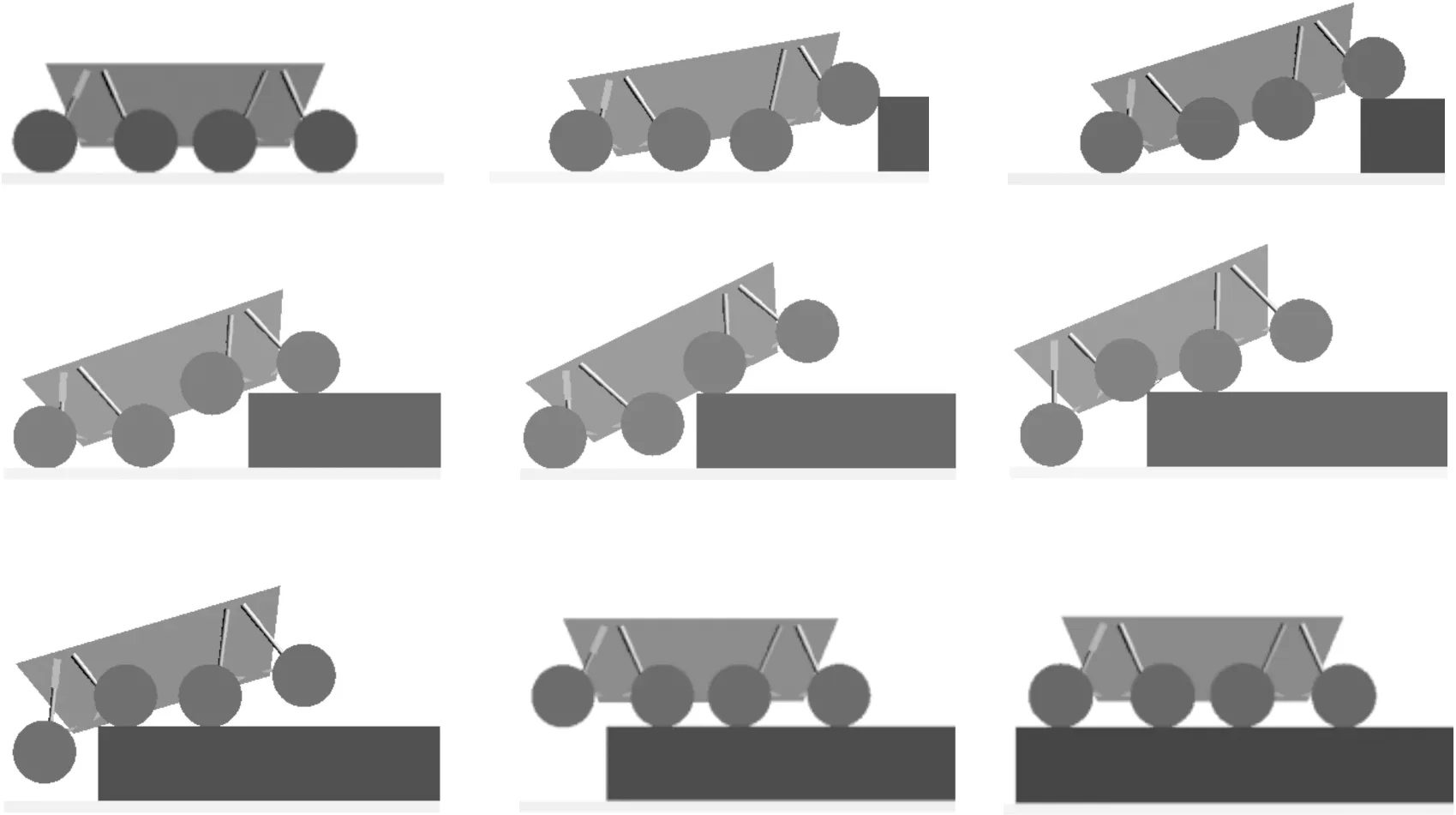
0.425 m

0.657 m

1.073 m

步态2:H≤0.520 8 m,中前轮可保持前轮越障的姿态,无需调整姿态可完成越障。

0.520 8 m

0.819 m

步态3:H≤0.433 m,中后轮无需调整姿态可完成越障。

0.433 m

0.803 m

1.023 m

步态4:全部悬挂回到中位,完成四轴越障。

3 越障性能仿真验证

为了能较为真实地仿真模拟测试无人车越障性能,降低实车越障的周期和成本,利用QT[15]、车控板卡、Simulink、Adams[16]构建综合仿真平台,如图11 所示,并以高度为1.2 m的垂直墙进行仿真验证。

图11 综合仿真平台的搭建

图11(a)为QT、Simulink、Adams系统闭环框图,图11(b)为综合仿真平台的硬件连接图,由地面站、车控底盘板卡、交换机以及用于模拟无人车产生动作的电脑组成。地面站、车控板卡、Adams无人车通过千兆以太网连接到交换机中。再将越障策略编写进车控板卡中,开始进行越障测试。

首先地面站用来下发越垂直墙指令数据帧,指令数据帧经过底盘板卡处理,将越障策略下发到Simulink中,Adams通过传感器获取到垂直墙的高度以及与质心之间的距离等信息,将反馈状态的遥测帧数据返回到车控板卡中,随后无人战车开始根据越障策略完成了1 200 mm的垂直墙越障。图12为无人战车完成垂直墙越障的全过程。

图12 垂直墙越障全过程

图13为越障过程的响应曲线。图13 (a)为越垂直墙过程战车质心的垂向位移变化曲线,可以看出越障过程质心变化平缓,垂直方向的位移约为1.2 m,说明无人战车能够越过1.2 m的垂直墙。图13(b)为质心前进方向的位移,前进过程速度变化较为平滑。图13(c)为液压缸的悬挂行程,可以看出各轴悬挂长度的变化与越障策略一致,验证了步态规划的合理性。

图13 越障过程响应曲线

4 结论

针对复杂地形环境,从步态规划和动力学的角度对一种8轮全液压驱动的轮腿式无人战车进行了越障分析,求取了轮腿式无人战车不同可越垂直墙高度下与各轴摆臂之间的关系式,为战车的控制策略提供了基础。利用QT、Simulink、Adams构建综合仿真平台,对战车越障性能进行仿真验证,研究表明:无人战车能够跨越1.176倍轮胎直径的垂直墙高度,具有高机动性和良好的越障性能,为8轮战车的实验测试提供了理论参考。