考虑吊杆断裂过程的下承式钢管混凝土拱桥动力分析

吴庆雄,罗健平,魏小康,徐召,管锡琨

(1.福州大学土木工程学院,福建 福州 350108;2.山东高速高商公路有限公司,山东 济南 251600;3.山东省交通规划设计院集团有限公司,山东 济南 250031;4.高性能桥梁结构交通运输行业重点实验室,山东 济南 250031)

0 引言

拱桥在桥梁结构中是一种重要的类型,拱桥按材料类型可分为钢拱桥、混凝土拱桥和钢管混凝土(concrete filled steel tubular,CFST)拱桥[1].从1990年第一座CFST拱桥修建以来,截止2015年1月,中国CFST拱桥数量就已达413座[2].如此庞大的数量及日益增长的交通量,使得在役CFST拱桥的安全性得到桥梁学者广泛关注.近年来,国内发生多起中、下承式拱桥因吊杆断裂而导致桥梁坍塌的事故[3-5].根据结构与受力特点,中、下承式拱桥悬吊桥面系又可分为3大类[6].虽然《钢管混凝土拱桥技术规范(GB 50923—2013)》[7]规定不再允许采用第三类桥面系,且规定根据桥梁使用状况对于在服役的3类桥面系宜进行加固改造,但现阶段仍然存在一定数量的第三类桥面系拱桥.因此,对拱桥吊杆断裂产生的冲击作用进行评估,为新建拱桥及现有拱桥设计改造提供依据,避免断索后桥面系发生落梁甚至坍塌的风险.

对于中、下承式拱桥因吊杆断裂而引发的悬吊桥面系发生连续坍塌的问题,Starossek[8]建议采用斜拉桥连续倒塌分析方法进行拱桥断索问题的分析,Theodore等[9]也证明该方法分析拱桥断索问题的可行性.在此基础上,国内外学者开展了一系列关于拱桥断索的研究.文献[10-12]以实际拱桥为工程背景,结合ABAQUS、ANSYS、MIDAS等有限元软件,进行了拱桥吊杆破断过程的模拟,主要分析了吊杆断裂位置、断索时间、载荷大小等对拱桥剩余结构受力性能影响.文献[13-17]采用等效静力计算法结合有限元或缩尺模型试验对中、下承式拱桥在吊杆断裂作用下动力响应及破坏模式进行分析,给出相应工况的动力系数.

综上所述,现有研究在静力分析方面,常将吊杆断裂效应通过在拱肋及加劲纵梁的吊杆锚固点处施加一对与原索力相等的作用力进行考虑,此方法将无法准确反应出吊杆断裂瞬间产生的动力放大效应,动力系数的取值偏小;而在动力分析方面,均为围绕某一特定桥梁进行分析,从现有研究可知,跨径、吊杆位置、桥面系布置等都会对动力系数的取值产生影响,故仅通过某一座拱桥的动力分析来获取吊杆断裂后的动力系数,其普适性有待验证.

为此,本研究以下承式CFST拱桥为研究对象,开展考虑吊杆断裂过程的下承式CFST拱桥动力系数取值研究.统计62座下承式CFST拱桥结构参数,构建具有代表性的标准拱桥.采用有限元软件进行吊杆断裂过程模拟,并采用已有模型试验实测数据对有限元模型进行精度验证,通过开展下承式CFST标准拱桥吊杆断裂作用下的静、动力对比分析,获取能够普遍适用于下承式CFST拱桥在吊杆断裂作用下采用等效静力计算法的动力系数,为下承式CFST拱桥强健性设计或加固提供参考.

1 构建下承式CFST标准拱

1.1 关键参数统计

本研究共收集62座下承式CFST拱桥相关资料.图1给出了下承式CFST拱桥跨径(L)分布随着时间的变化趋势,可以看出多数下承式CFST拱桥的跨径集中在50～150 m.各跨径占比分布见图2.从图2可看出跨径为50 m≤L<100 m,100 m≤L<150 m和L≥150 m的下承式CFST拱桥分别只占总数的41.9%,51.6%和6.5%.限于篇幅,仅给出跨径100 m≤L<150 m下承式CFST拱桥统计数据.

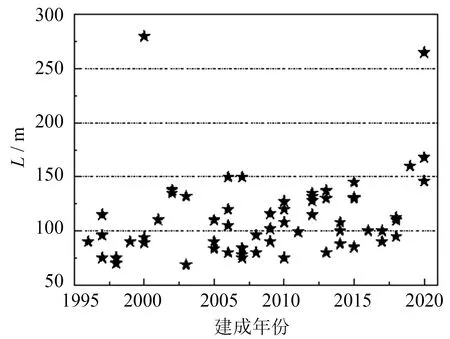
图1 跨径年代分布Fig.1 Span distribution of time

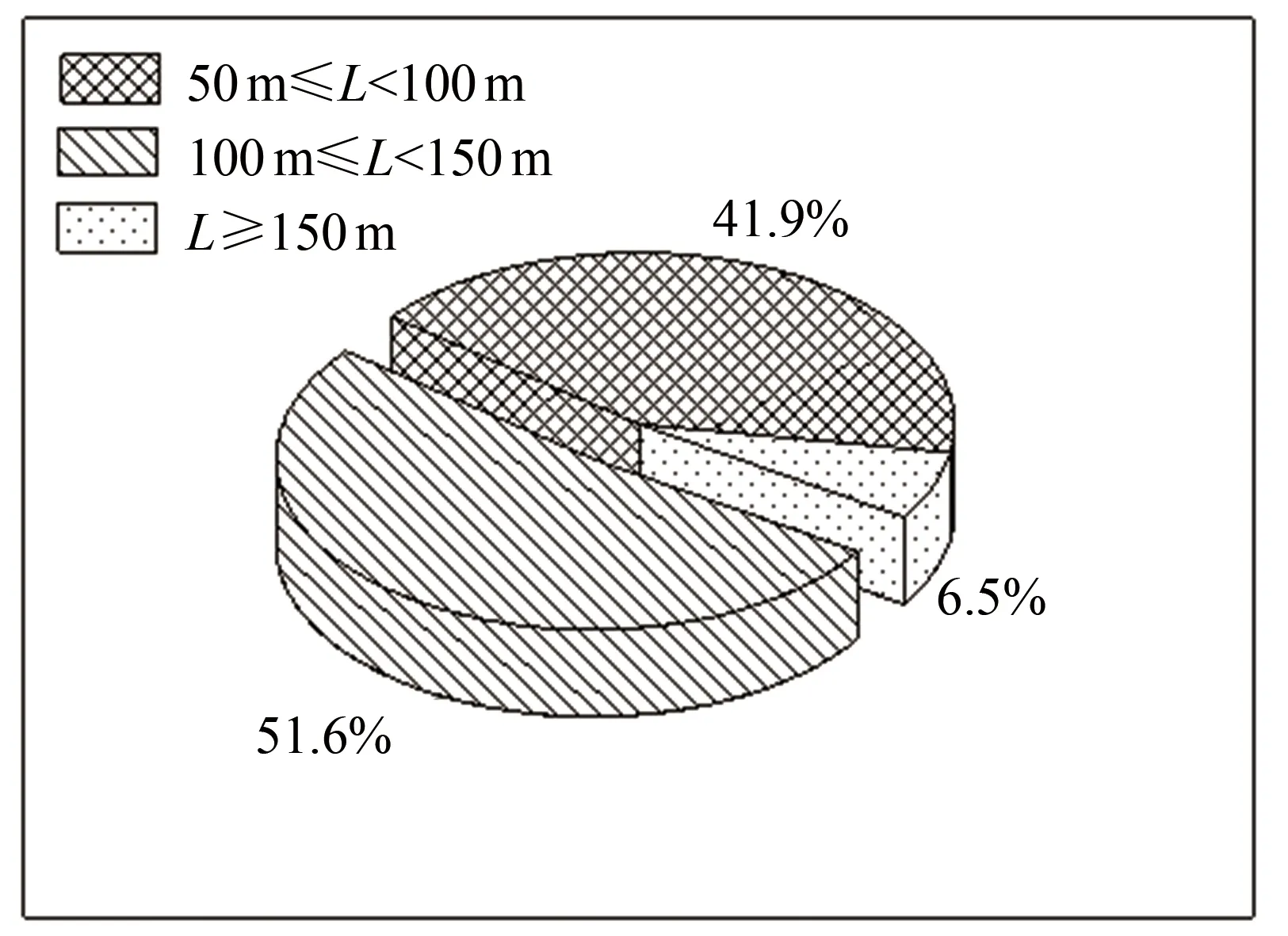
图2 跨径分布比例Fig.2 Span distribution proportion

CFST拱桥关键构造参数比重见图3,由图3可知,跨径100 m≤L<150 m下承式CFST拱桥拱肋矢跨比为1/5的桥梁占比最大为75%.拱轴线形中悬链线所占比例最高为80%,是该跨径范围内主要的拱轴线形.Q345钢应用最多,占比59%.拱肋截面则以哑铃型截面应用的比例最大,达70%.

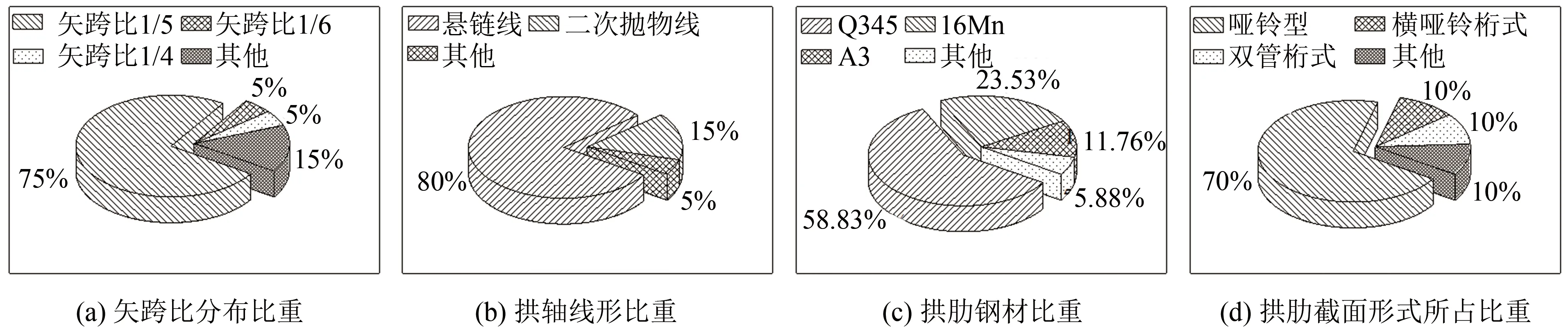
图3 下承式CFST拱桥关键构造参数比重Fig.3 Proportion of key structural parameters of through CFST arch bridge

1.2 标准拱桥构建

1.2.1标准拱构建方法

根据下承式CFST拱桥设计关键参数[18]的统计分析结果,取各参数统计分析平均值构建虚拟拱桥,并以跨径相近的实际拱桥为参考对象,构建下承式CFST标准拱桥.下面给出构建跨径125 m的下承式CFST标准拱桥的过程.

1.2.2下承式CFST标准拱

参考东莞大北汾特大桥[19]结构参数,对统计得到的虚拟拱桥各参数进行修正,从而构建标准拱桥.拱桥各关键参数详见表1.标准拱跨径为125 m,矢跨比为1/5,拱轴线采用悬链线的形式,拱肋钢材采用Q345钢,管内灌注C50混凝土,拱肋截面形式为哑铃型,拱肋高度为3 m,吊杆间距为5.68 m,吊杆采用单根7Ф5的预应力钢绞线.下承式CFST标准拱桥总体布置如图4所示.对构建的125 m下承式CFST标准拱桥进行设计复合验算,满足设计规范[20]要求.

采用上述标准拱构建方法,构建了跨径分别为85、95、…、135 m的下承式CFST标准拱桥.

表1 拱桥主要参数

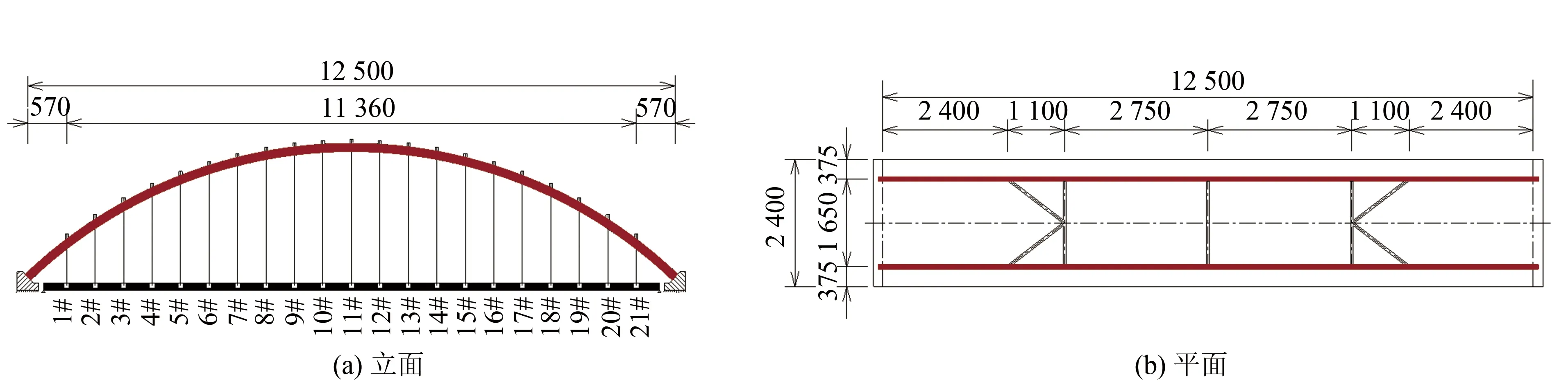
图4 125 m标准拱桥总体布置与主要截面(单位: cm)Fig.4 General layout and main sections of 125 m standard arch bridge (unit: cm)

2 考虑吊杆断裂的有限元建模方法

2.1 有限元模型建立

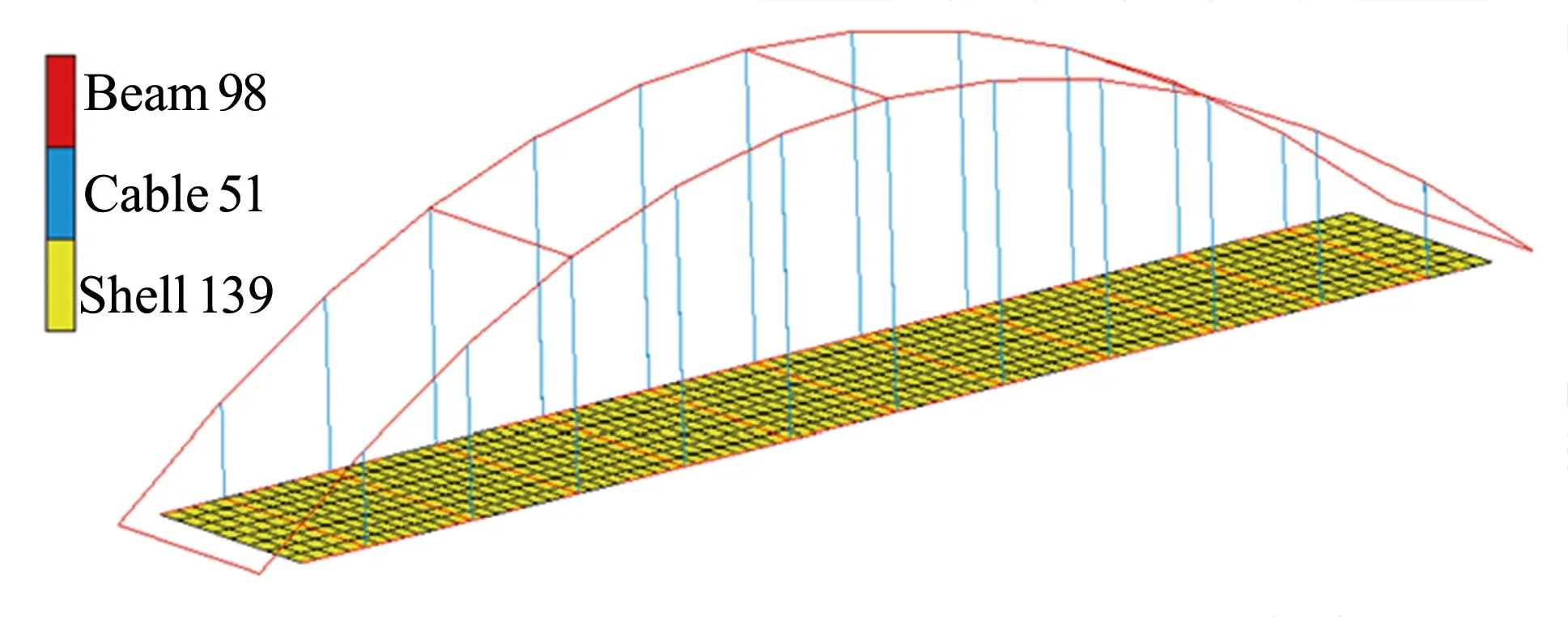
图5 缩尺试验桥有限元模型Fig.5 Finite element model of scale test bridge

采用MSC.Marc软件建立文献[21]中的试验模型.该试验模型跨径20 m,矢跨比为1/5,拱肋中心横桥向间距2.86 m,吊杆采用单根7Ф5的预应力钢绞线,全桥共设11对吊杆,纵向间距1.67 m.在有限元模型中,采用Beam 98弹性梁单元模拟拱肋、横梁、纵梁和横撑等结构,其中每侧拱肋96个单元,加劲纵梁88个单元,并采用双单元法对钢管混凝土结构模拟;吊杆采用Cable 51索单元模拟;桥面板等采用Shell 139单元模拟;各材料参数根据规范规定取值;边界条件为拱肋拱脚固结,拱桥加劲纵梁两端为简支.有限元模型如图5所示.

2.2 吊杆断裂模拟

利用MSC.Marc瞬态动力学模块及生死单元技术模拟吊杆断裂产生对拱肋、纵梁等构件的冲击过程.其中动力学瞬态分析可以计算任意载荷历程的响应[22],拱桥的断索行为类似碰撞行为,会使得拱桥悬吊桥面系、吊杆等产生大变形,故断索情况下拱桥的受力分析为非线性分析.MSC.Marc软件中生死单元技术为断索的实现提供了可能,模拟过程如图6所示.在进行下承式CFST拱桥断索分析时,引用文献[21]中断索装置所测得的断索时间,以及文献[14]中所实测结构阻尼.即断索时间取0.1 s,结构阻尼取0.02.

图6 吊杆断裂有限元模拟示意Fig.6 Schematic diagram of finite element simulation of suspender fracture

3 有限元动力计算结果分析

本研究选取1#短吊杆、2#次短吊杆及6#长吊杆这三对吊杆分别断裂时,对拱桥剩余结构受力情况进行分析,吊杆编号见图6.

3.1 拱肋动力响应

吊杆断裂前后拱肋动力响应如图7所示.由图7(a)可知: 1#短吊杆断裂,断裂吊杆对应的拱肋截面应力值(σ)最大为-37.23 MPa.2#次短吊杆断裂,断裂吊杆对应的拱肋截面应力值最大为-43.83 MPa;6#长吊杆断裂,断裂吊杆对应拱肋截面应力值最大为-47.43 MPa.由图7(b)可知,长吊杆断裂时,拱肋吊点处产生位移(S)最大为4.73 mm.综上可得,当吊杆断裂时,断裂吊杆对应拱肋截面的应力值最大,即断裂吊杆对应拱肋截面为最不利截面.其中长吊杆断裂对拱肋受力影响最大.从受力情况看,吊杆断裂情况下拱肋应力变化值虽较大,但对于采用Q345钢的拱肋,其承载能力仍然具有一定的安全富余.

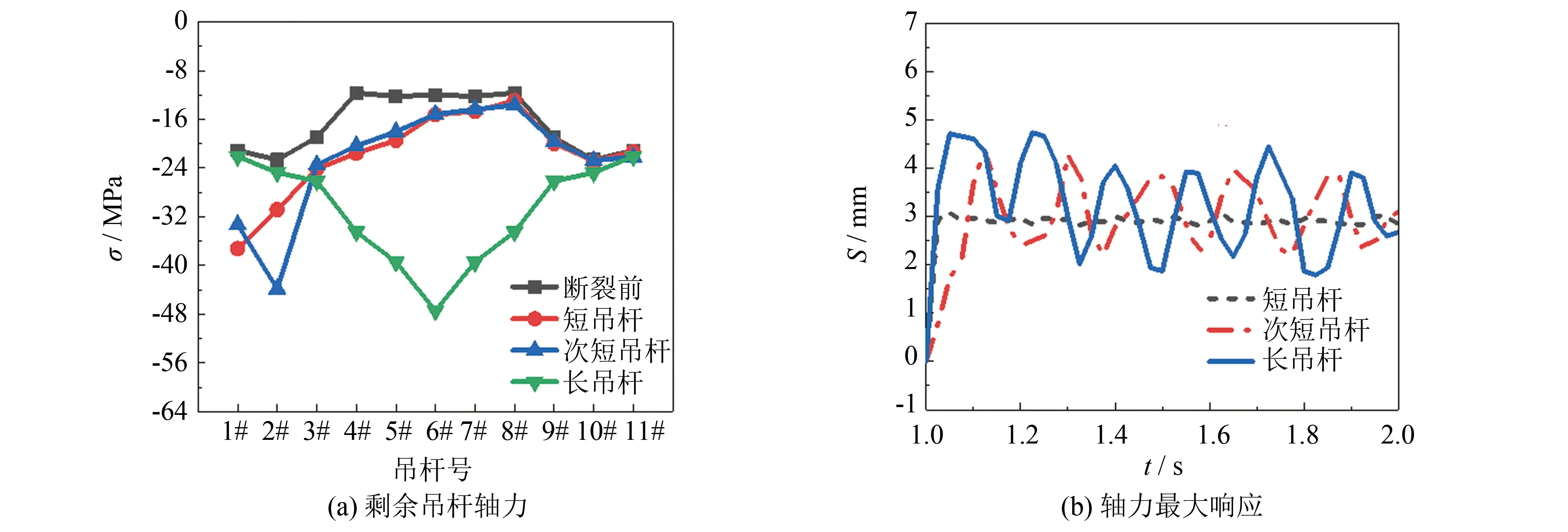
图7 吊杆断裂前后拱肋动力响应Fig.7 Dynamic response of arch rib when suspender fracture

3.2 悬吊桥面系加劲纵梁动力响应

吊杆断裂前后纵梁截面动力响应如图8所示.由图8(a)可知,当1#短吊杆、2#次短吊杆、6#长吊杆分别断裂,加劲纵梁在各断裂吊杆位置所对应截面的应力值(σ)最大,分别为4.19、6.85、10.42 MPa.由图8(b)可知,长吊杆断裂时,加劲纵梁吊点处产生位移(S)最大为15.21 mm;当长吊杆断裂时,加劲纵梁应力最大截面动力响应明显要大于次短吊杆与短吊杆断裂.综上可得,长吊杆断裂对于悬吊桥面系加劲纵梁的动力响应影响最大,且断裂吊杆位置对应加劲纵梁截面为最不利截面.各吊杆断裂,使得采用C50混凝土的加劲纵梁出现开裂甚至断裂的可能.

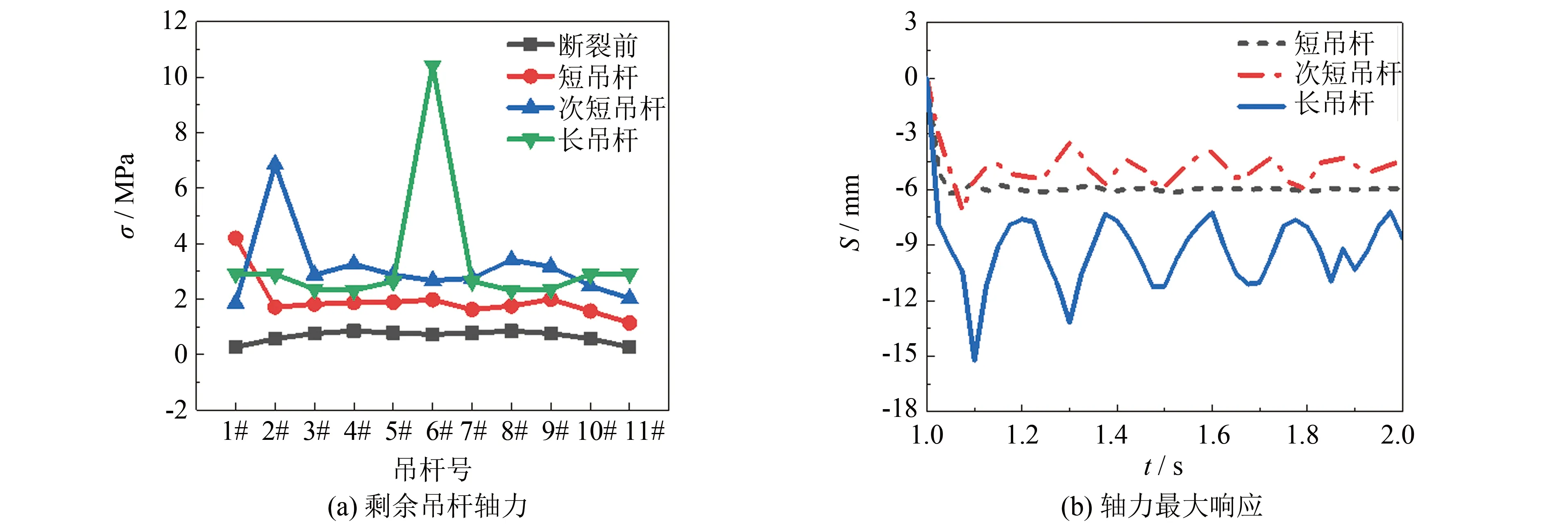
图8 吊杆断裂前后纵梁截面动力响应Fig.8 Dynamic response of longitudinal beam when boom fracture

3.3 吊杆动力响应

吊杆断裂前后剩余吊杆受力如图9所示.由图9(a)可知: 1#短吊杆断裂,相邻2#吊杆轴力(F)最大为36.23 kN;2#次短吊杆断裂,相邻3#吊杆轴力最大为39.45 kN;6#长吊杆断裂,相邻5#和7#吊杆轴力最大为37.13 kN.由图9(b)可知,当次短吊杆断裂时,剩余吊杆中产生的最大动力响应最大.综上可得,吊杆断裂对于剩余吊杆轴力会产生较大的影响,其中次短吊杆断裂对相邻吊杆轴力的影响最大,为最不利工况.由文献[21]可知,吊杆的极限拉力为80 kN,而当次短吊杆断裂时,相邻3#吊杆轴力为39.45 kN,已达到极限拉力的1/2,且吊杆为拱桥中易损部件,故应对剩余吊杆的受力情况予以关注.

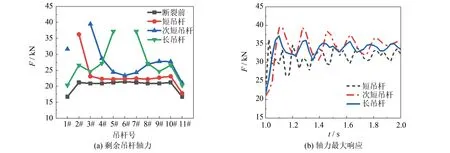
图9 吊杆断裂前后剩余吊杆受力图Fig.9 Stress diagram of remaining suspenders before and after suspender fracture

3.4 有限元模型精度验证

有限元模型参照文献[21]中的试验模型进行建模,试验模型实测数据与有限元建模所分析结果对比如表2所示.由表2可得,有限元模拟计算值与试验实测值最大偏差为11.25%,因此认为本研究所采用MSC.Marc有限元软件进行下承式CFST拱桥断索分析具有良好的精度.

表2 吊杆断裂有限元与试验结果最值对比

4 考虑吊杆断裂作用的动力系数计算

4.1 动力系数理论

为简化下承式CFST拱桥在吊杆断裂所产生的冲击作用下动力分析过程,引入动力系数(μD),以此得到准确的动力响应最大值.即假设吊杆断裂后,拱桥各部件(拱肋、纵梁、吊杆等)仅受到吊杆断裂时初始索力(N0)释放所产生冲击作用.在断裂吊杆的吊点处施加一对大小相等、方向相反的集中力(ND),按静力分析方法计算吊杆断裂后下承式拱桥剩余结构在ND和N0作用下的静力响应.动力系数的表达式为

μD=ND/N0

(1)

式中:μD为动力系数;ND为吊杆断裂后施加集中力;N0为吊杆的初始索力.

4.2 动力系数计算

以第1节所构建125 m下承式CFST标准拱桥为例,采用第2节有限元建模方法,假定动力系数分别取1.0、1.1、…、2.0,开展125 m下承式CFST标准拱桥吊杆断裂后剩余结构的静力响应分析.最后将静力与动力计算结果进行对比,从而得到具有普适性的动力系数(μD).

4.2.1吊杆动力系数

各吊杆断裂前后剩余吊杆最大响应及动力系数如图10所示.由图10(a)可知,吊杆断裂时,相邻吊杆轴力最大.图10(b)为各吊杆分别断裂后相邻吊杆最大动力响应,各工况对应最大动力响应值列于表3.从图10(b)和表3可知,2#次短吊杆断裂前、后,相邻吊杆轴力最大.图10(c)为假定各吊杆动力系数从1.0～2.0所对应静力响应.由图10(c)可知,当1#短吊杆、2#次短吊杆、11#长吊杆分别断裂,动力系数(μD)取1.554、1.728、1.663时,各工况静力响应与动力响应最大值相等.即对于125 m下承式CFST拱桥,发生吊杆断裂时,剩余吊杆的动力系数(μD)取为1.728时,静力计算法能获得与动力计算法最大值一致的结果,且计算结果偏于安全.

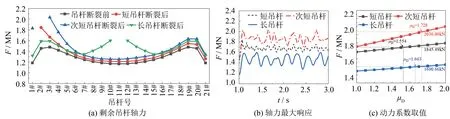
图10 各吊杆断裂前后剩余结构最大响应及动力系数取值Fig.10 Maximum response and dynamic coefficient value of the remaining structurewhen the suspender fracture

表3 各吊杆断裂后相邻吊杆及纵梁截面最大动力响应值

4.2.2加劲纵梁动力系数

各吊杆断裂前后加劲纵梁截面最大响应及动力系数取值如图11所示.由图11(a)可知,吊杆断裂时,断裂吊杆位置处加劲纵梁截面应力最大.图11(b)为各吊杆分别断裂后加劲纵梁截面最大动力响应,各工况对应最大动力响应值亦列于表3.由图11(b)和表3可知,11#长吊杆断裂对应加劲纵梁截面应力最大.图11(c)为假定各吊杆动力系数从1.0～2.0所对应静力响应.由图11(c)可知,当1#短吊杆、2#次短吊杆、11#长吊杆分别断裂,动力系数(μD)取1.623、1.717、1.764时,各工况静力响应与动力响应最大值相等.即对于125 m下承式CFST拱桥,发生吊杆断裂时,加劲纵梁的动力系数(μD)取为1.764时,静力计算法能获得与动力计算法最大值一致的结果,且计算结果偏于安全.

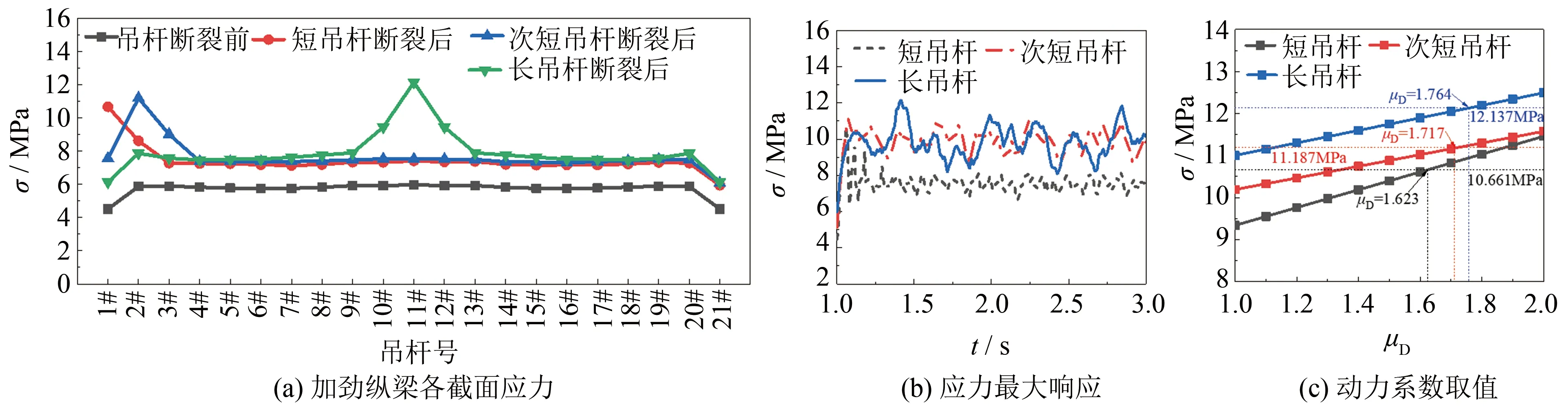
图11 各吊杆断裂前后加劲纵梁截面最大响应及动力系数取值Fig.11 Maximum response and dynamic coefficient value of stiffened longitudinal beam sectionwhen the suspender fracture

4.2.3125m下承式CFST拱桥动力系数取值

对于125 m下承式CFST标准拱桥,在进行吊杆断裂动力分析时,吊杆等效静力计算动力系数(μD)可偏保守地取为1.728;加劲纵梁等效静力计算动力系数(μD)可偏保守地取为1.764.

4.3 下承式CFST拱桥动力系数取值

本研究构建85、95、105、115、125、135 m跨径拱桥,采用动力系数计算方法,得到短吊杆、次短吊杆、长吊杆分别断裂时动力系数与跨径之间的关系,如图12所示.

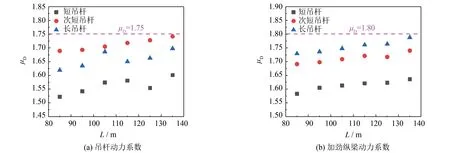
图12 不同跨径下承式拱桥动力系数Fig.12 Dynamic coefficient of through arch bridge with different spans

由图12可知,常见跨径下承式CFST拱桥在采用等效静力计算法进行动力分析时,吊杆动力系数(μD)可偏保守地取1.75,加劲纵梁的动力系数(μD)可偏保守地取1.80.

5 结语

1) 统计分析62座下承式CFST拱桥,得到不同跨径范围的矢跨比、拱轴线形、拱肋截面形式、纵梁刚度、吊杆截面积等结构参数.以实际桥梁为参考,构建了125 m下承式CFST标准拱桥.

2) 采用MSC.Marc有限元软件模拟下承式CFST拱桥吊杆断裂的全过程,通过与试验实测数据对比,模拟结果最大误差仅为11.25%,模拟方法具有良好精度,能够在下承式CFST拱桥断索分析中推广使用.

3) 有限元分析表明: 下承式CFST拱桥在吊杆断裂时,拱肋和加劲纵梁各截面在断裂吊杆所对应位置为最不利截面,剩余吊杆则是断裂吊杆的相邻吊杆为最不利吊杆.其中长吊杆断裂对拱肋和加劲纵梁的动力响应影响较大,次短吊杆断裂对剩余吊杆的动力响应影响较大.

4) 构建6种不同跨径下承式CFST标准拱桥,通过对动力系数的取值分析表明: 当剩余吊杆和悬吊桥面系加劲纵梁的动力系数(μD)分别取1.75和1.80时,采用静力计算法得到的静力值,与动力分析结果基本一致,结果可靠且偏于安全.