曲率半径对小净距超大断面隧道地震响应的影响

谷音,何建,阙云,柳林齐,蓝亦辉

(1 .福州大学土木工程学院,福建 福州 350108;2.上海城建市政工程(集团)有限公司,上海 200065)

0 引言

我国属于地震多发地带,地震不仅严重威胁隧道结构安全,而且可能会切断交通路线、延误救灾工作[1-6].近年来,国内外学者对隧道地震响应的研究均已取得丰硕成果.于媛媛等[7]通过试验和动力有限元法,研究隧道衬砌的地震响应.孙铁成等[8]研究发现隧道洞口段仰拱和墙角处为不利位置,应予以重视.刘博清等[9]建立隧道洞口段三维有限元模型,分析隧道洞口段在不同软岩弹性模量(E)、泊松比(ν)和坡度下的动力响应规律.汪树华等[10]通过研究衬砌刚度和厚度对动力响应结果的影响,提出墙角、拱腰处刚度适当减小、其余地方刚度适当增大的刚度分配原则和薄拱厚墙的衬砌尺寸设计创新思路.赵占雷[11]采用动力有限元法分析总结各因素对隧道地震动力响应的影响规律.蒋树屏等[12]利用有限元分析与大型振动台试验相结合的方法,研究埋深对隧道结构动力响应特性的影响,建议在高烈度地震区修建山岭隧道时,隧道埋置深度应尽量不小于50 m;皇民等[13]以雅沪高速某山岭隧道为原型,运用大型振动台模型试验,研究浅埋错距双洞山岭隧道洞口段震害特征与工程减震措施,结果表明隧道仰坡拱肩45°位置是隧道洞口段的薄弱环节,应予以重视.马帅等[14]利用有限元方法,将曲线隧道和直线隧道在地震作用下的位移(d)与应力进行对比分析,发现曲线隧道各部位的位移和应力均大于直线隧道.周彦良等[15]在普通直线隧道抗震研究的基础上,分析研究曲线隧道的震害特性和震害作用机理,确定影响曲线隧道地震反应特性的因素,提出降低曲线隧道震害的对策,认为隧道曲线段与直线段的结合部位为曲线隧道的一个抗震分析重点部位.穆嘉豪等[16]建立小半径平面曲线隧道三维分析模型,探讨其在单向水平激振下的地震响应规律.

上述研究分别采用数值分析、模型试验等多种手段,分析地震波作用下隧道地下结构的地震响应并提出减震措施,反映当今隧道抗震、减震分析的前沿水平和研究热点.但以上研究大多针对直线隧道,对曲线隧道的研究为数不多,且有关曲线隧道的研究均集中在圆形等截面形式简单的隧道上.随着城市基建发展的需要,小净距超大断面隧道逐渐增多.但是,不同曲率半径(r)下小净距超大断面曲线隧道的地震动力响应尚不明晰.

鉴于此,有必要进一步分析隧道曲率半径对小净距超大断面隧道地震动力的影响.本研究以长乐龙门隧道为研究对象,采用数值分析方法,研究曲率半径对小净距超大断面隧道地震动力响应的影响.

1 计算模型和计算工况

1.1 工程背景

长乐龙门隧道为分离式隧道,由南向北呈S形走向.隧道全线为小净距山岭隧道,其最小净距为12.59 m,最大净距为20.76 m.左线隧道长度为658 m,右线隧道长度为671 m.单洞最大跨度为20.41 m,最大开挖面积为247.41 m2.根据国际隧道协会定义,隧道横断面大于100 m2的隧道即为特大断面隧道,故长乐龙门隧道属于特大断面隧道.同时,隧道两洞室间距小于一倍洞室间距,属于小净距隧道.隧道模型以长乐龙门隧道为对象,如图1所示,隧道横断面形状为马蹄形四心圆,取水平洞径为19.21 m.

1.2 计算模型

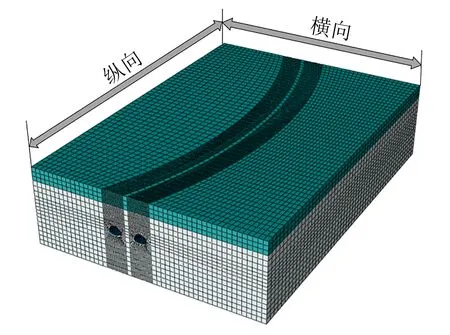
图2 模型示意图Fig.2 Model diagram

为揭示不同曲率半径对小净距超大断面隧道地震响应特征的影响,利用ABAQUS软件建立5种三维实体模型.5种隧道模型的曲率半径分别为400、600、800、1 000和∞ m.曲率半径为400 m的隧道模型,其长、宽、高分别为500、420、120 m;曲率半径为600、800、1 000 m的隧道模型,其长、宽、高分别为500、350、120 m;曲率半径为∞ m的隧道模型是直线隧道模型,其长、宽、高分别为500、300、120 m.上述隧道模型均为双洞隧道,两洞室间距均为19 m,隧道埋深均为50 m,模型示意图如图 2所示.

隧道的初期支护和二次衬砌采用弹性本构关系,围岩采用Mohr-Coulomb弹塑性本构关系,地表为Ⅴ级围岩,隧道所在地层为Ⅳ级围岩,锚杆加固区采用围岩加固区模拟,模型具体参数如表 1所示.c为粘聚力、φ为摩擦角.为提高计算效率,对隧道和周边网格进行加密,其他部分则未进行加密.计算模型均采用C3D8R三维实体8节点减缩积分单元.根据谷音等[17]和何建涛等[18-20]的相关研究,模型采用粘弹性人工边界作为边界条件,通过ABAQUS自带弹簧阻尼器来吸收耗散地震能量,以达到无限远场的模拟效果.

表1 围岩和衬砌的力学参数

1.3 计算工况

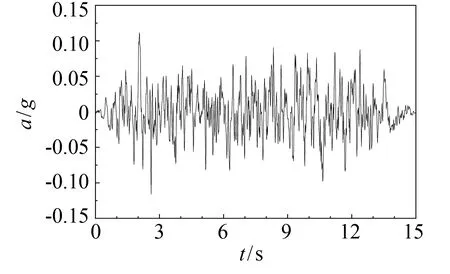
图3 人工波地震波时程曲线Fig.3 Artificial seismic time-history curve

本研究所用地震波是根据长乐地区场地条件合成的,峰值加速度(a)约为0.1g,出现时刻为第2.06秒,如图 3所示.受计算条件的限制,本次计算采用包含峰值在内的15 s地震波.根据皇民等[21]的研究,在横向激励下,隧道结构地震动力响应更加强烈,同时由于曲线隧道线形在纵向上有变化,故沿横向和纵向同时输入地震波,如图2所示.参考何建涛等[18-20]的相关研究进行地震输入,将地震波加速度时程转化为速度时程曲线和位移时程曲线,同时考虑模型初始地应力,计算施加在模型边界节点上的等效节点力.

2 试验结果与分析

为避免模型边界效应的影响,在数据分析时,忽略头尾50 m范围内的计算结果,只取中间部分.左右线隧道各取拱顶、左拱肩、左拱腰、左拱脚、仰拱、右拱肩、右拱腰、右拱脚为隧道截面监测点,如图1所示,曲线隧道根据弯曲方向分为凹侧(左侧)与凸侧(即右侧).

2.1 横向地震作用

1)内力响应分析.图4～6分别为隧道各监测点的峰值内力.在横向地震作用下,左右线隧道各监测点的内力峰值分布规律相同.随着曲率半径的减小,峰值弯矩(M)和剪力(F剪)在拱顶处逐渐增大、在拱腰和拱脚处逐渐减小,峰值轴力(F轴)在左拱肩和拱脚处逐渐增大、在右拱肩和拱腰处逐渐减小.从隧道各监测点内力峰值可以看出,隧道拱脚处的峰值内力均大于其他监测点.曲率半径为400 m的曲线隧道与直线隧道相比,其左洞拱顶和仰拱处峰值弯矩增大95%,左拱脚处的峰值弯矩减小87%;其右洞拱顶和仰拱处峰值弯矩增大95%,右拱脚处的峰值弯矩减小79%.

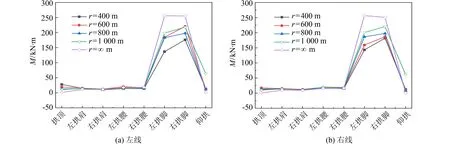
图4 横向地震作用下的峰值弯矩Fig.4 Peak moment under lateral earthquake action

图5 横向地震作用下的峰值剪力Fig.5 Peak shear force under lateral earthquake action

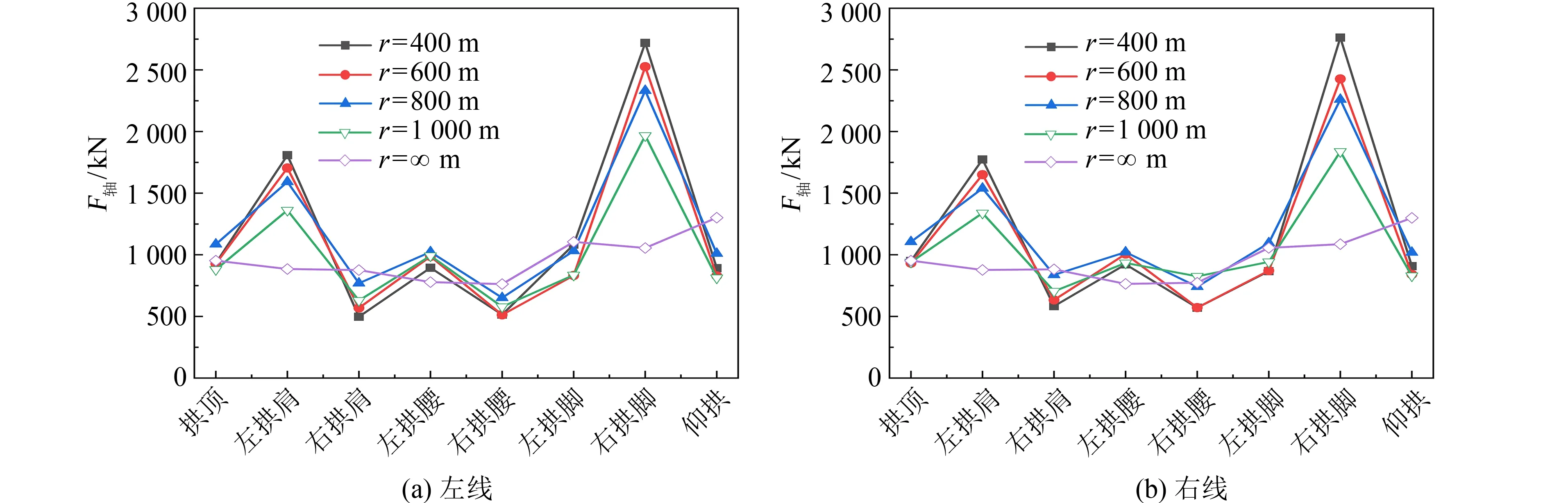
图6 横向地震作用下的峰值轴力Fig.6 Peak axial force under lateral earthquake action

图7为隧道右拱脚相较于左拱脚的内力增长率.在横向地震作用下,隧道曲率导致隧道右侧监测点的内力大于左侧监测点,且隧道曲率半径越小,两侧内力差距越大.轴力受隧道曲率的影响最大,当曲率半径为400 m时,隧道左洞右拱脚处的峰值轴力比左拱脚处增大3.36倍,隧道右洞右拱脚处的峰值轴力比左拱脚处增大3.44倍.

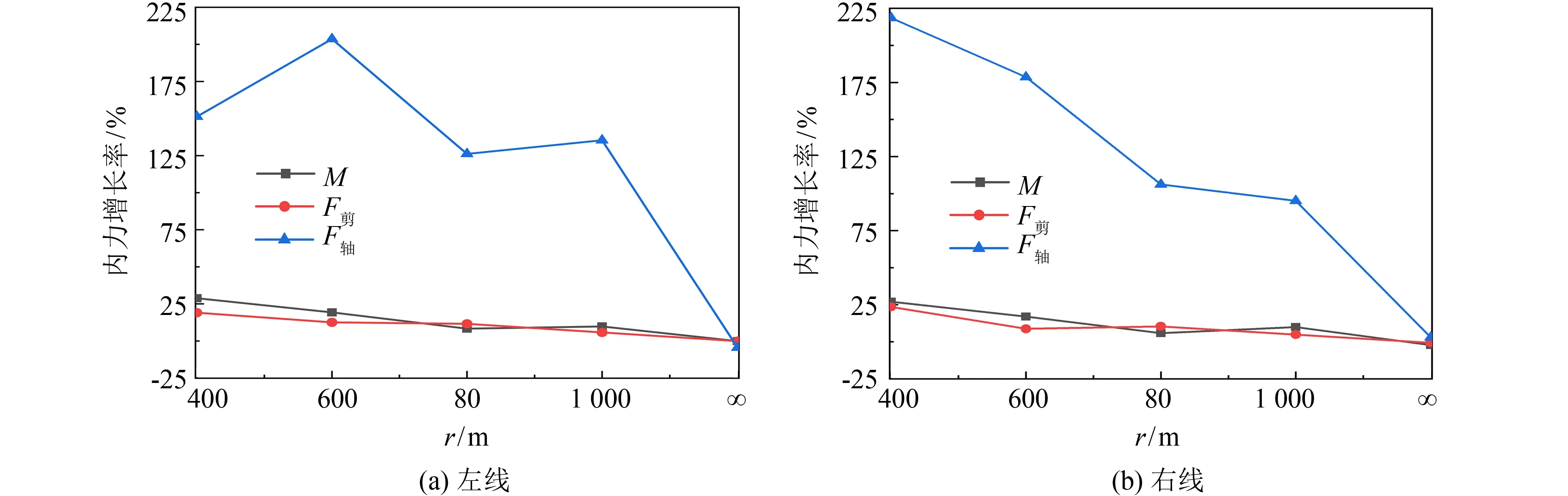
图7 横向地震作用下右拱脚的内力增长率Fig.7 Force growth rate of the right arch foot under lateral earthquake action

2)位移响应分析.图8为隧道监测点的峰值位移.在横向地震作用下,当隧道曲率半径为1 000 m时,隧道的峰值位移达到最大,当曲率半径为600 m时次之,当曲率半径为400 m时,隧道的峰值位移最小.峰值位移在各监测点拱顶处最大、仰拱处最小,峰值位移随着埋深增大呈减小的趋势.当曲率半径为1 000 m时,左线隧道拱顶处的峰值位移为0.302 m,相较于直线隧道(峰值位移为0.296 m)增大0.53%;右线隧道拱顶处峰值位移为0.302 m,相较于直线隧道(峰值位移为0.297 m)增大0.47%.由此可见,隧道的峰值位移响应受曲率的影响较小,变化幅度不超过1%.

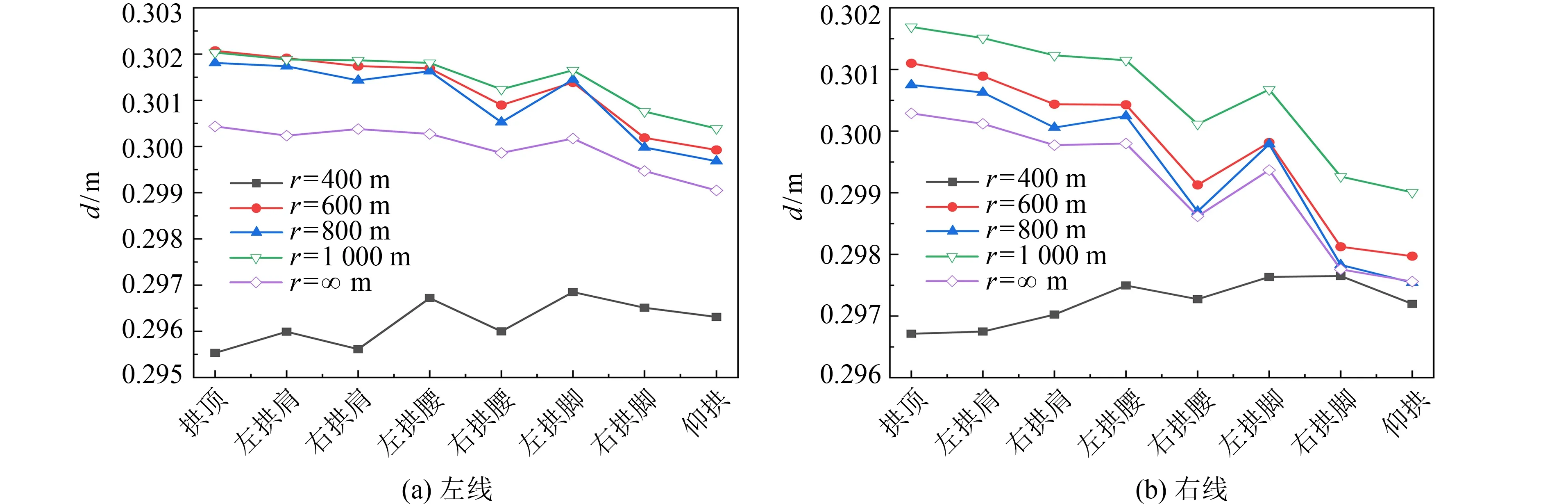
图8 横向地震作用下的峰值位移Fig.8 Peak displacement under lateral earthquake action

2.2 纵向地震作用

1) 内力响应分析.图9～11为隧道监测点的内力峰值.在纵向地震作用下,左右线隧道各监测点的内力峰值分布规律相同.随着曲率半径的减小,峰值弯矩和剪力在隧道拱顶处逐渐增大,在拱腰和拱脚处逐渐减小;峰值轴力在隧道左拱肩和拱脚处逐渐增大,在右拱肩和拱腰处逐渐减小.从隧道各监测点内力峰值可以看出,隧道拱脚处的峰值内力均大于其他监测点.相较于直线隧道,当曲率半径为400 m时,曲线隧道左洞拱顶和仰拱处峰值弯矩增大86%,左拱脚处的峰值弯矩减小50%;右洞拱顶和仰拱处峰值弯矩增大72%,左拱脚处的峰值弯矩减小50%.

图10 纵向地震作用下的峰值剪力Fig.10 Peak shear force under longitudinal earthquake action

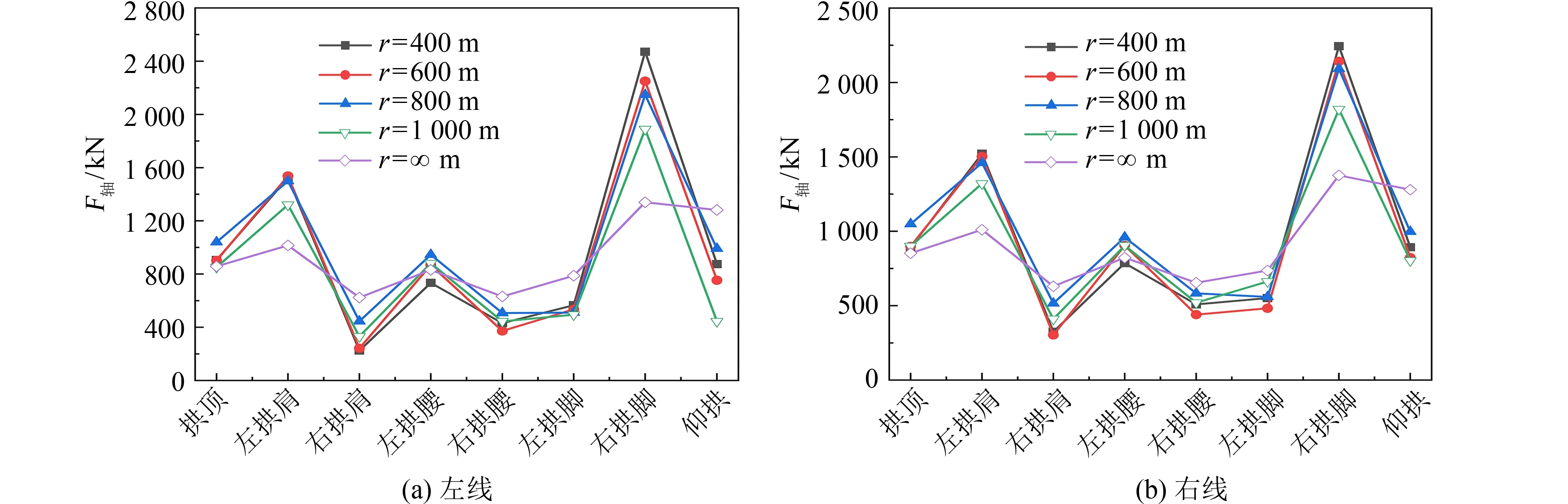
图11 纵向地震作用下的峰值轴力Fig.11 Peak axial force under longitudinal earthquake action

图12为隧道右拱脚相较于左拱脚的内力增长率.在纵向地震作用下,隧道曲率导致隧道右侧监测点的内力大于左侧监测点,且随着隧道曲率半径的减小,两侧内力的差距增大.轴力受隧道曲率的影响最大,当曲率半径为400 m时,隧道左洞右拱脚处的峰值轴力比左拱脚处增大1.51倍,隧道右洞右拱脚处的峰值轴力比左拱脚处增大2.18倍.

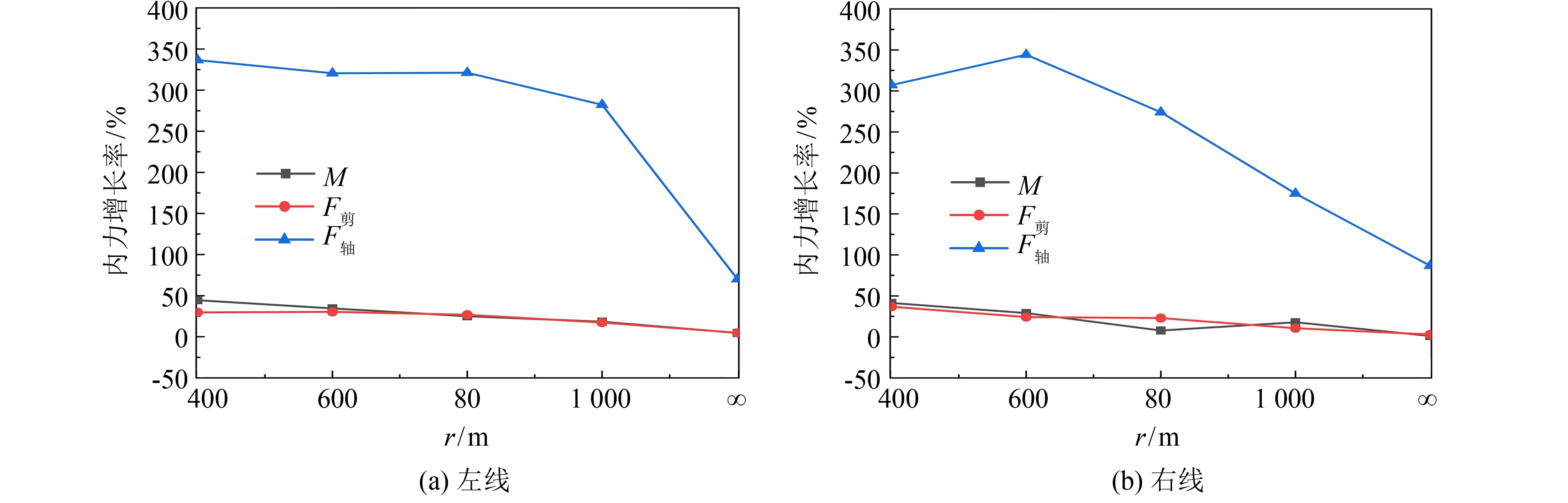
图12 纵向地震作用下右拱脚的内力增长率Fig.12 Force growth rate of the right arch foot under longitudinal earthquake action

2) 位移响应分析.图13为隧道监测点的峰值位移.在轴向地震的作用下,隧道的峰值位移响应也随隧道曲率半径的减小而增大.曲率半径为400 m的曲线隧道位移最大,而直线隧道位移最小.曲率半径为600、800和1 000 m的曲线隧道峰值位移差值较小,而曲率半径为400 m的曲线隧道峰值位移有显著的增大.

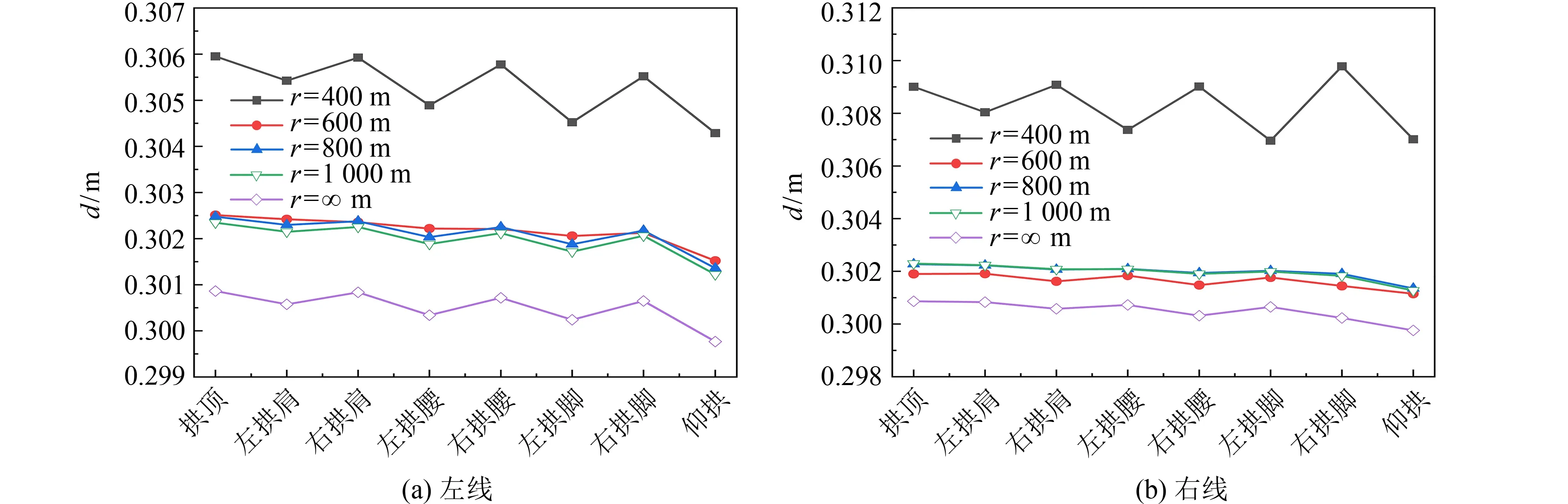
图13 纵向地震作用下的峰值位移Fig.13 Peak displacement under longitudinal earthquake action

3 结语

建立小净距超大断面隧道模型,运用黏弹性边界方法和等效节点力输入方法模拟地震波输入,探究曲率半径对小净距超大断面隧道的影响规律.

1) 在地震作用下,小净距超大断面曲线隧道的拱脚处为薄弱位置,其内力均大于其他监测点,且随着隧道曲率半径的变化,隧道拱脚处各项内力的动力响应变幅最大.

2) 随着曲率半径的减小,小净距超大断面曲线隧道结构各监测点峰值位移增大,但增幅较小,仅为1%左右.

3) 曲率半径对小净距超大断面曲线隧道各监测点处内力的影响不同,随着曲率半径的减小,隧道拱顶和仰拱处的弯矩、剪力随之增大,而隧道拱腰和拱脚处的弯矩、剪力、轴力随之减小.

4) 在地震作用下,受曲率半径的影响,隧道左侧和右侧监测点的内力和位移差异较大,右侧监测点的内力大于左侧监测点,且曲率半径越小,两侧的内力差距越大.因此,在隧道设计时应重视隧道曲率半径的影响.