高考情境化试题分析研究
2023-05-30赵国威彭乃霞张力江苏臣
赵国威 彭乃霞 张力 江苏臣







【摘 要】 通过对2016—2022年所有全国高考试卷(全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷、全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷)进行统计,对试卷中的情境型试题按照题目数量、综合难度系数、知识点涵盖面以及相关变化趋势等方面进行分析,得到以下研究结论:高考逐渐注重情境型题目的考查;不同年份之间情境型试题的综合难度系数彼此差距不大,情境型试题能够更好地均衡难度因素,全面考查学生的综合素养;情境型题目着重考查基础性知识,重在培养学生的综合应用能力. 依据结论,期望为教师在课堂实践中提供教学建议与参考.
【关键词】 情境型试题;应用能力;创新能力;综合难度系数
1 问题提出
《中国高考评价体系》中“四层”和“四翼”指出,学生在面对与数学学科相关的生活实践或学习探索情境中的问题时,要具备分析问题、解决问题的综合能力与学科知识,在命制试题时要选择合适的实际生活情境,发挥核心价值的引领作用,让学生运用必备知识和关键能力解决问题,全面发展学生的学科素养水平[1]. 可见,情境型试题是考查学科核心素养的重要载体,情境也是高考评价体系中的考查载体[2]. 《国家中长期教育改革和发展规划纲要(2010—2020年)》中强调,强国必先强教,新时代下的教育要提升学生的综合素质,增强学生服务国家、服务人民的社会服务能力,提升学生勇于探索、勇于创新的科学研究能力,培养学生善于解决问题的实践能力[3]. 《国务院关于深化考试招生制度改革的实施意见》中指出,我国考试招生制度旨在选拔德、智、体、美、劳全面发展的社会主义建设者与接班人,在公平公正的基础上,增强基础性和综合性,着重考查学生的独立思考和运用所学知识分析问题、解决问题的能力[4].
我国课程标准改革以来,经历了从双基到三维目标,再到四基与核心素养,对学生综合实践能力的考查逐渐增加,注重数学在生活中的实际应用. 2017版《普通高中数学课程标准》在课程性质这一板块强调了“数学的应用已渗透到当今社会及人们生活的各个方面”,课程基本理念这一板块中也明确指出课程的内容要重视数学与生活、数学学科与其他学科之间的联系、提升学生用数学知识解决实际问题的能力. 必修课程和选修课程中也分别加入了数学建模与数学探究活动,用来加强学生学到的知识与生活之间的联系[5]. 这预示着我国高中数学教学越来越重视数学应用意识,因此提高数学应用意识,也是顺应现今数学教育改革的基本趋势.
情境化试题是利用学生的认知结构解决现实生活中存在的实际问题,着重考查学生解决问题的能力,这些试题将学生置于实际生活情境中,能够有效落实学生的学科核心素养[6]. 数学情境化试题指的是以真实存在于自然界与生活中的数学现象、或相关数学历史为背景材料,联系生活经验的一类试题. 情境型试题的解决需要学生在阅读情境中进行数据分析获取关键信息,解决相应的数学问题. 情境型试题最大的特点是题目取自于现实生活,注重书本知识与现实生活的联系,体现了数学的学科核心素养,强调学生要学会用数学的眼光观察生活,用数学的思维思考世界的观点. 数学应用意识是一种认知活动,是学生通过运用习得的数学观点、数学方法以及学习技能在进行探究活动时所经历的感觉、知觉、记忆和思维等过程的综合反应,是一种碰到问题时不仅具备运用数学观点和数学方法去解决问题的心理倾向,而且伴随着数学思维的行为产生[7]. 学生通过所掌握的习得数学知识和数学技能,以数学的视角主动地进行观察、感知,进行分析事物和现象,再借助数学语言、逻辑推理、思想技能等来描述和解决所面对问题的一种认知活动. 它建构于学生对数学的学习特点和对应用价值的理解认识之上,数学应用意识可以帮助学生学会用数学的视角看生活.
2 问题设计
以课程标准改革为分界线,通过对2016年至今所有多省份参与的高考试卷(全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷、全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷)进行统计,对试卷中的情境型试题按照题目数量、综合难度系数、知识点涵盖面以及相关变化趋势等方面进行分析.
2.1 研究对象
2016—2020年的全国高考试题分为全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷,2020年课程标准进行修订后,2021年和2022年的全国高考试题分为全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷. 将2016—2022年的高考真题进行划分,其中因新高考Ⅰ卷与新高考Ⅱ卷不区分文理,故对于新高考Ⅰ卷与新高考Ⅱ卷单独进行分析. 全国甲卷依据适考地区应与全国Ⅲ卷进行对比分析,全国乙卷依据适考地区归入到全国Ⅱ卷进行分析.
2.2 研究框架
本文从 2016—2022年全国高考数学试题中的数学应用题目出发,研究数学应用能力在高考试题中的渗透情况,并根据相应的结果提出有关促进学生数学综合应用能力教学的建议,提升学生的综合素养,落实学生核心素养的培养. 以 2016—2022 年全国高考卷中的数学情境型试题为研究对象,对数学高考试题进行文本分析,探究其渗透的情况. 借助武小鹏的综合难度系数模型[8],采用定量分析法對高考试题中数学情境型试题的数量、难度系数、知识点涵盖面以及相关变化趋势进行量化分析,以此分析数学情境型试题在高考试题中的考查情况. 根据分析结果对数学课堂教学提出建议,期望能够为教师在进行课堂教学时提供参考意见.
3 问题结果与分析
3.1 题目数量统计分析
从试题的数量进行统计分析,结果如图1所示. 从图中可以看出情境型题目的数量总体呈现增长趋势,在试卷中所占分值也在逐步增大. 《中国高考评价体系》依据国家发展所需人才特质和素质教育的培养目标提出高考的四个考查要求—四翼. 四翼中的应用性强调,高考要注重学以致用,在命题时要坚持理论联系实际原则,注重贴近生活,贴近社会,要利用日常生活中的实际问题,培养学生运用数学知识、数学能力以及自身综合素养解决实际问题的能力[2]. 由此可以进行合理推断,高考情境型试题的数量会保持一个稳定的速率进行增长. 因此教师在进行教学过程中,要注重数学知识与实际生活的联系,让学生在日常学习生活中潜移默化地提升自身的综合素养.
3.2 题目难度统计分析
借助武小鹏教授的综合难度系数模型[8]、鲍建生教授的课程综合难度评价模型[9]对高考中情境型题目的难度系数进行计算,一级因子只取背景因素,其划分水平如表1所示,利用背景因素难度系数模型di=∑jnijdijn,其中∑jnij=n,i=1,2,3…. 依照综合难度系数模型对于背景因素的定义,将试题划分完毕后由高校教师与一线教师对分析结果进行一致性检验,由此得出2016—2022年情境型题目的难度系数,结果如表2所示.
由表2可以看出,每一年不同地区的考试试卷其情境型题目的难度系数变化幅度不大,涨幅在平均值附近上下波动,表明情境型题目的设置能够体现高考的公平性.
以试卷类别为维度,从图2中可以看出,全国Ⅰ卷从2016年题目的难度系数逐步提升,于2019年达到峰值,2020年趋于平缓. 全国Ⅱ卷的题目一直在上下波动,从2018年开始呈现增长趋势. 全国Ⅲ卷题目的难度系数相较于另外两套试卷的难度系数是较低的,总体保持一个稳定增长的趋势,足以体现出高考试题充分考虑了地域教育因素的差别,从而在试题命制的数量与难度方面进行了合理的分配,体现了高考的平等性与公平性原则. 从图3中可以看出,虽然新高考试卷(2021—2022年)数据较少,但也能看出难度系数呈现一个平稳增加的趋势. 由图2和图3综合来看,情境型题目的难度会有所上升,也表明情境型题目会强调多个知识点和多个素养的综合考查指标,由此可以看出高考试卷在把握试题整体呈现效果的基础上在慢慢增加情境型题目在高考试题中的占比,因此教师应增强对于数学应用能力培养的重视程度. 由此可推断出,高考将会逐渐偏重于对情境型题目的考查,且更加强调数学知识与实际生活之间的联系,强调学生核心素养的综合发展.
3.3 题目考查知识点统计分析
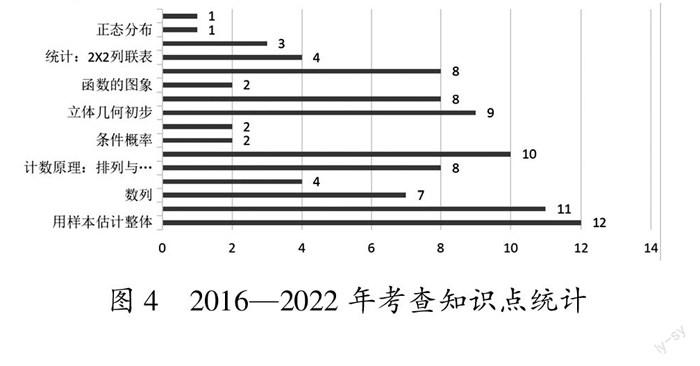
将2016—2022年全部情境型试题所考查的数学知识点进行统计,借鉴《普通高中数学课程标准(2017年版2020年修订)》对课程结构的划分,将高中知识点分为必修课程、选择性必修课程以及选修课程,其中必修课程包括预备知识(集合,常用逻辑语,相等关系与不等关系,从函数观点看一元二次方程与一元二次不等式)、函数(函数概念与性质,幂函数、指数函数和对数函数,三角函数,函数应用,数列,一元函数导数及其应用)、代数与几何(平面向量及其应用,复数,立体几何初步)、统计与概率(计数原理,统计,概率)、数学建模与探究活动;选择性必修课程包括函数(数列,一元函数导数及其应用)、几何与代数(空间向量与立体几何,平面解析几何)、概率与统计(计数原理,概率,统计)、数学建模活动与数学探究活动[5];同时借助《普通高中数学课程标准(2017年版2020年修订)》中的六大核心素养,将试题所考查的素养能力进行划分,得出数学情境型高考题所涉及的数学知识点以及对应的核心素养统计,结果如图4所示. 依照《普通高中數学课程标准(2017年版2020年修订)》对于核心素养的定义,将试题进行划分,划分完毕后由高校教师与一线教师对分析结果进行一致性检验,由此得出2016—2022年考查核心素养的统计表,结果如图5所示.
由图4和图5可以看出,近几年的高考数学全国卷的情境型题目对于各个知识点均有涉及,其中以概率与统计为背景进行考查较为广泛,情境型题目同样能够综合考查学生六个核心素养的运用能力,对应考查较多的核心素养为数据分析、数学运算与逻辑推理. 题目对应的知识点常见于概率与统计模块的用样本估计整体,主要以生活背景和综合背景为主,其中也含有大量的数学史、数学文化等科学背景的渗透. “概率与统计”试题的本质在于反映数学源于生活,又应用于生活. “概率与统计”试题对于学生阅读能力的考查也越来越高[10].
可以发现,数学情境型题目的考查比较注重基础性,注重对基础部分内容的应用,结合日常生活或学习实践中遇到的素材,并与其他学科进行联结,增强应用性,加强创新应用意识的考查,教师在进行教学时应当注意对数学基础知识的讲解,针对于基础知识要讲细讲全,帮助学生构建坚实牢固的基础. 同时,数学情境型题目更加注重各数学知识之间的整合,强调数学知识体系之间的相互联系,这便要求教师在进行教学时应当帮助学生从总体上感知数学,以基础知识点为地基从整体上建构数学认知结构体系,注重数学核心素养的综合发展.
4 问题结论与建议
通过对近7年高考数学全国卷试题的分析,得到全国卷(全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷、全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷)情境型试题的考查具有以下结论:数学高考试卷逐渐重视数学情境型试题的考查. 这表明通过选取适当的生活素材或科学素材,构建问题情境,让学生在真实生活背景下综合运用数学学科素养,用必备知识和关键能力去解决真实问题,全面综合发展学科素养水平[2]. 高考试题在情境类型题目方面综合难度系数相差不大. 这表明情境型试题能够更好地均衡难度因素,全面考查学生的综合素养,既能够缓和整套试卷的综合难度,又能够更好地检测出学生的真实水平,将数学高考的积极导向作用和选拔人才作用充分发挥. 全国卷中情境型试题所考查的知识点大多以预备知识为中心进行考查,能够综合考查六大核心素养. 这表明情境型试题强调基础扎实,更加关注学习者在未来生活或学习中所必须具备的学习知识和学习能力,数学学科所蕴含的逻辑推理能力、数据分析与处理能力,数学所使用的归纳思想、推理方法均能在此类型的试题中得到考查. 通过对试题的分析,得出以下教学建议.
4.1 注重生活中的知识积累,增强创新应用意识
来自现实生活中实际情境强调知识之间的融合,能够综合考查学生的核心素养,能够让学生更好地把握数学的本质,启发思考. 学生从情境型试题中寻找题目条件,以自身的认知结构抽象出数学模型,有效考查学生数据分析、信息提取的能力,以及模型建构的科学思维. 加强数学考试试题与真实情境的融合,对学生感悟数学的学科价值、应用价值、文化价值和审美价值起到增强作用,同时对逻辑推理、数学建模、数据分析等学科核心素养的考查和建构都具有十分重要的意义. 重视情境与问题的结合,将问题与情境融为一体,提高情境与问题结合的程度,加深学生对情境的理解,在情境中分析问题、解决问题的能力,从而有效培养、高效考查学生对所学数学知识的掌握和核心素养水平.
例1 (2022年全国甲卷选择题第2题)某社区通过公益讲座以普及社区居民的垃圾分类知识.为了解讲座效果,随机抽取10位社区居民,让他们在讲座前和讲座后各回答一份垃圾分类知识问卷,这10位社区居民在讲座前和讲座后问卷答题的正确率如图6,则( ).
A.讲座前问卷答题的正确率的中位数小于70%
B.讲座后问卷答题的正确率的平均数大于85%
C.讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D.讲座后问卷答题的正确率的极差大于讲座前正确率的极差
该试题以普及社区居民进行垃圾分类知识的讲座为试题背景,利用问卷答题正确率为题目数据,要求学生从图表中精确提取数据,考查学生预备知识中概率与统计部分的用样本估计总体的集中趋势参数,同时也考查了学生对于统计图表的数据分析能力,通过对数据的整理、分析和推断,最终作出正确选择,体现了高考想要考查学生综合运用能力的改革方向.
因此,教师在进行教学时,应当以数学来源于生活为教学重点,注重知识点与国家时政相互融合,注重知识点在真实生活情境中的处理,将知识点的讲解转变为思想方法的讲解,提升学生获取信息的能力,增强进行定量分析的意识和数据表达现实生活的问题意识,可以将生活情境中产生的问题作为新课程的课前导入素材,进行生活中的知识积累,建立数学知识与生活知识之间的联系,依托数据探索事物本质,加强创新意识与应用意识的培养,学会用数学的眼光观察所处的世界.
4.2 加强基础性知识的讲解,注重内在知识的迁移与理解
高考试题中,一部分试题所提供的情境与问题之间存在一定的关联,该类试题所考查的知识点均属于必修模块中学生要求掌握的基础知识,学生分析所给情境,从情境中获得有用信息进行解答,主要考查学生的理解能力与知识迁移能力,对创新能力的考查相对薄弱. 《中国高考评价体系》指出,简单的情境活动主要对应“四翼”中的基础性要求,重点关注学生在未来的生活、学习中应当具备的基本知识与能力. 通过对题目的阅读理解,概括出对应的数学概念,利用得到的新概念进行题目求解,培养学生数学抽象、直观想象以及数学运算等数学核心素养.
例2 (2022年新高考Ⅰ卷单选题第4题)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库. 已知该水库水位为海拔148.5 m时,相应水面的面积为140.0 km2 ;水位为海拔157.5 m时,相应水面的面积为180.0 km2. 将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5 m上升到157.5 m时,增加的水量约为( )(7≈2.65 ).
A.1.0×109 m2 B.1.2×109 m2
C.1.4×109 m2 D.1.6×109 m2
該试题以南水北调工程为试题背景,利用水库的相应数据为题目数据,令学生抽象概括出一个底面积为180.0 km2,上底面积为140.0 km2,棱台高为9m的新棱台,考查学生预备知识中几何与代数部分的立体几何初步中棱台体积的计算公式,以现实世界中物体的形状、大小为载体考查学生直观想象、数学抽象等核心素养,以及数据提取能力与运算能力. 该类试题的考查体现了高考的基础性以及学生融会贯通的能力,因此教师在进行教学时应当注重知识之间的迁移,将知识进行单元化备课,帮助学生搭建知识点与知识点之间的联结.高中数学涉及的知识点多且杂,在进行课程授课设计过程中,需要遵循一定的规律安排,并且结合课程标准设置出符合学生基础的教学目标. 在进行设计之前,应当充分理解学习内容对应的内涵与外延,认清学情,同时要紧跟时政步伐,理清暗藏在知识点之间的脉络,将新的合适的教学方法适时融入课堂教学中,更好地培养学生核心素养的形成.
例3 (2022年新高考Ⅱ卷单选题第3题)中国的古建筑不仅是挡风遮雨的住处,更是美学和哲学的体现. 如图7是中国某古建筑物的剖面图,AA′,BB′,CC′,DD′是桁,DD1,CC1,BB1,AA1是脊,OD1,DC1,CB1,BA1是相等的步,相邻桁的脊步的比分别为DD1OD1=0.5,CC1DC1=k1,BB1CB1=k2,AA1BA1=k3,若k1,k2,k3是公差为0.1的等差数列,直线OA的斜率为0.75,则k3=( ).
A. 0.75 B. 0.8 C. 0.85 D. 0.9
该试题以中国古建筑屋顶的建构为试题背景,利用屋顶的相应数据为题目数据,令学生利用数据之间满足的关系进行计算,考查学生函数模块中对数列定义的理解,以现实世界中物体的形状、大小为载体考查学生数学运算、直观想象等核心素养,该题目还涉及对学生的题目理解能力的考查,是否能通过文字描述想象出模型的大体形状,通过等差数列与直线斜率知识点交叉融合,考查学生综合能力的应用.
因此,教师在进行教学时,应当以基础知识为教学重点,不要过多地在难题、偏题等数学竞赛试题上耗费学生精力. 加强学生对于基本概念和基础知识的掌握,教师的教学应当促进学生理解概念的内涵,扎实的基础知识是产生迁移的基础. 同时也应加强知识点之间的整合,强调数学各个分支之间的相互交叉与渗透,帮助学生从宏观上建构知识框架,在学生的已有认知结构之上,构建新的知识结构,教会学生用数学的思维思考世界.
4.3 加强逻辑推理能力的发展,培养学生综合性发展
数学是培养理性思维的重要途径[11]. 逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质[5]. 通过选取社会现实存在的热点问题,以提供多种形式的材料进行设问,引导学生进行独立的思考与判断. 该类型的试题不仅考查学生综合运用所学知识的能力,同样也能考查学生融会贯通的方法,学生的逻辑推理与数据分析等核心素养均能得到考查.
例4 (2022年全国乙卷选择题第10题)某围棋手与甲、乙、丙三位棋手各比赛一盘,各盘比赛结果相互独立.已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3,且p3>p2>p1>0.记该棋手连胜两盘的概率为p,则( ).
A. p与该棋手和甲、乙、丙的比赛次序无关
B. 该棋手在第二盘与甲比赛,p最大
C. 該棋手在第二盘与乙比赛,p最大
D. 该棋手在第二盘与丙比赛,p最大
该试题以中国围棋为试题背景,融入必修模块的概率与统计中随机事件的独立性,动用学生的数据分析与逻辑推理能力,深入考查了学生对概率的理解. 通过题目所给信息,利用其中的棋局输赢逻辑关系,学生需要从文字叙述中抽象出判断信息,选出最终的答案,体现了高考注重全面发展的改革方向.
因此,教师在教学过程中,应当将培养学生的归纳、类比与演绎能力融入到学习中,针对学生逻辑推理能力的培养也有助于学生的创新能力与应用意识的发展. 对课堂中所教授知识重点、难点进行深度挖掘,在学生已有逻辑推理能力的建构基础上展开教学,帮助学生更好地建构逻辑推理素养,将逻辑思维能力融入生活,也体现了课程标准中理论与实践相结合的教学理念.
5 结束语
通过对7年所有全国高考试卷(全国Ⅰ卷、全国Ⅱ卷、全国Ⅲ卷、全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷)进行统计,对试卷中的情境型试题按照题目数量、综合难度系数、知识点涵盖以及相关变化趋势等方面进行分析,借助高考试题研究领域的相关文献,从中国高考评价体系入手,试题总体体现出知识与生活紧密联系的特点,情境型题目作为将知识、能力、价值进行综合考查的载体,能够更好地均衡难度因素,全面考查学生的综合素养. 真实情境往往与社会实际是紧密相连的,情境型题目既保留了知识的基础性考查作用,又强调了知识在生活中的综合应用,对高考数学课程教学以及课程改革提供了重要的参考方向.
参考文献
[1] 教育部考试中心.中国高考评价体系[M].北京:人民教育出版社,2019.
[2] 教育部考试中心.中国高考评价体系说明[M].北京:人民教育出版社,2019.
[3] 中华人民共和国教育部.国家中长期教育改革和发展规划纲要(2010—2020年)[EB/OL].[2010-7-29].
[4] 国务院.国务院关于深化考试招生制度改革的实施意见[M].北京:人民出版社,2014.
[5] 中华人民共和国教育部.普通高中数学课程标准(2017年版2020年修订)[M].北京:人民教育出版社.2020.
[6] 巫阳朔.情境化试题的设计、开发与编制规范[J].教学与管理,2017(07):78-81.
[7] 汪国华.数学应用意识的再认识及研究的方向[J].数学教育学报,2006(01):89-91.
[8] 武小鹏,张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报,2018,27(03):19-24.
[9] 鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望,2002,31(09):48-52.
[10] 薛欢,杜剑南,路江江.2016—2020年高考数学(理科)全国卷“统计与概率”试题探析——基于综合难度模型[J].教育测量与评价,2020(12):30-40.
[11] 晨旭.突出逻辑推理 加强应用能力考查——2014年全国高考数学试题评析[J].中国考试,2014(10):14-17.
[12] 赵轩,任子朝,翟嘉祺.新高考数学应用能力考查研究[J].数学通报,2021,60(03):22-24.
作者简介 赵国威(1996—),女,山东曲阜人;主要研究中学数学教育;主持省级课题一项、校级课题一项;已发表论文3篇.
彭乃霞(1960—),女,山东济南人,教授;主要研究中小学教育教学.
张力(1997—),男,贵州遵义人;主要研究中学数学教育.
江苏臣(1982—),男,贵州都匀人,教授;主要研究中小学教育教学.
