2022年全国高考圆锥曲线大题新特点综述及教学建议
2023-05-30唐宜钟


【摘 要】 本文综述了2022年圆锥曲线大题的四个新特点:载体更加丰富,双曲线备受青睐;“点”视角直线方程成为“新宠”;圆锥曲线与函数综合性问题加强;特殊性质、高观点结论为命题“源头”.最后给出了教学建议.
【关键词】 圆锥曲线;新特点;教学建议
2022年高考全国共有8份试卷,提供了8个圆锥曲线大题(其中全国甲乙卷文理同题).这些试题,无疑为高考圆锥曲线大题研究提供了一个良好的资源.纵观近3年来圆锥曲线大题,
笔者认为2022年圆锥曲线大题呈现出一些新特点,简述如下.
1 新特点综述
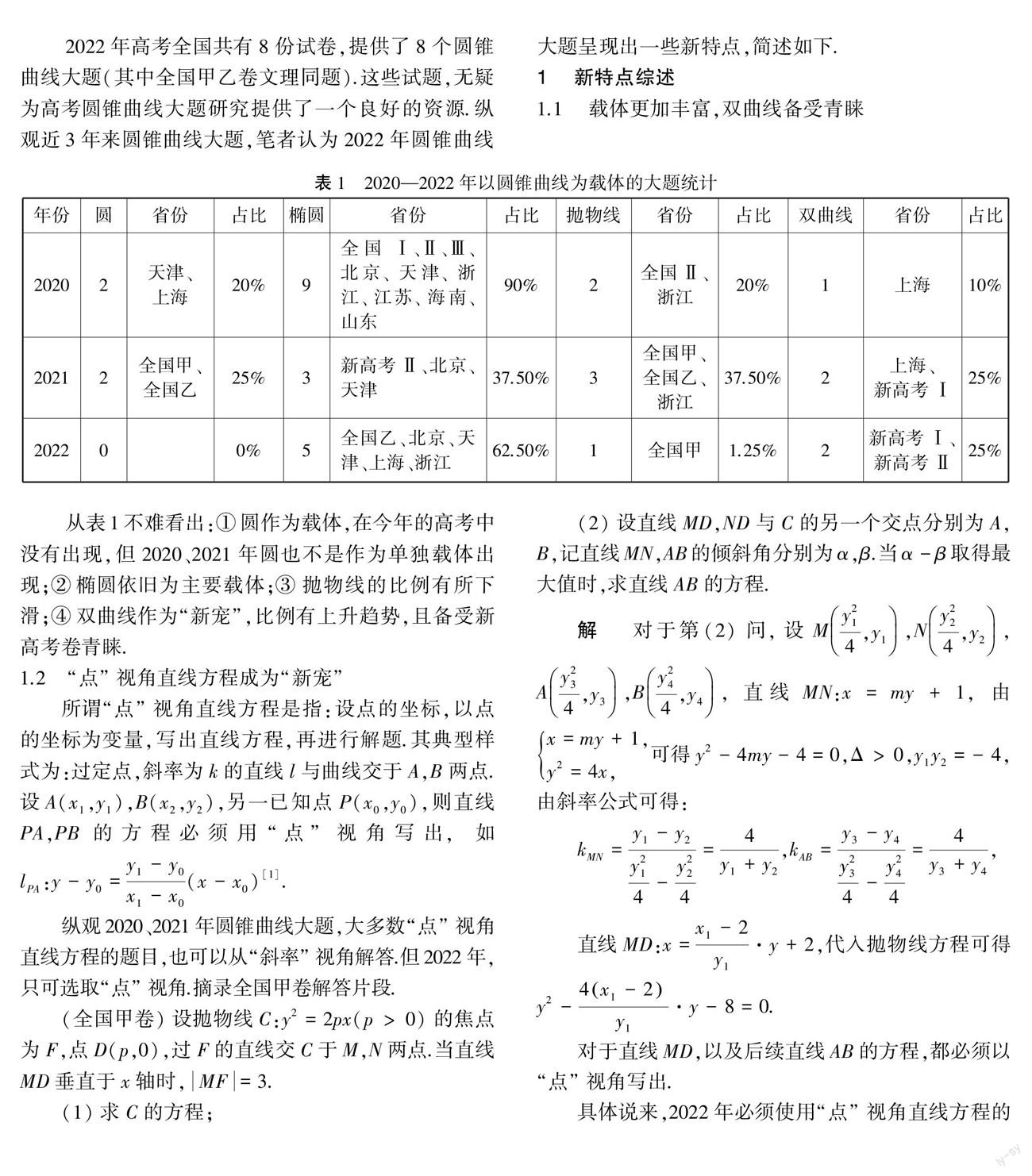
1.1 载体更加丰富,双曲线备受青睐
从表1不难看出:①圆作为载体,在今年的高考中没有出现,但2020、2021年圆也不是作为单独载体出现;②椭圆依旧为主要载体;③抛物线的比例有所下滑;④双曲线作为“新宠”,比例有上升趋势,且备受新高考卷青睐.
2 复习建议
2.1 扩大范围,关注通性通法,加强解题模式培养
不能将圆锥曲线大题的练习局限于椭圆和抛物线.许多老师在平时训练中,默认双曲线不会作为大题出现.这样一来,使学生的认知产生了偏差;另外,使学生错失了通过对比双曲线与椭圆、抛物线在解答上的异同,失去了更深刻、更全面理解解析几何的机会.近年来,圆锥曲线大题变化更加多样,一些解答更是变成了玄学.但其实,万变不离其宗,圆锥曲线常用的解决程序只包括以下四个方面:①方程联立:包括直线与直线联立、直线与曲线联立、曲线与曲线联立.这类联立最终达成的结果是减少未知量,或直接得出坐标等;②条件转化:常见的是直接将坐标、斜率、弦长、向量、面积等量的表征转化为可计算的符号化语言,或将抽象叙述、几何语言等转为直观理解的可计算的代数语言;③减少参量:利用题目中的条件,将参量个数变少或者建立起多个参量间的等式,或者利用不等式、临界范围等将某个参量定量消除;④计算化简:包括根据条件最终计算出点的坐标、斜率、直线曲线方程等,并化简为要求的或者约定俗成的形式,或者利用已知范围计算出某个所求值的范围或最值.只要按照流程,关注通性通法,加强解题模式培养,学生定能有所突破.
2.2 稳定心态,明确计算方向,加强运算能力培养
圆锥曲线问题初看来,往往式子繁杂.在平时训练中,要培养学生稳定的心态和时间管理意识.要规划好时间,不急不缓,注重细节,避免非知识性失误.适当鼓励,加强学生信心,克服其畏难情绪.同时,加强代数技巧、不等式方法的培养,提供简算、巧算、估算技巧.如在判别式的计算中,并不需要将所有常数全部相乘,得到最终结果.而是将每个常数进行素因式分解,关注其偶次方式,因为判别式最终要进行开方.在2020年全国乙卷中,可以进行平移变换,将A(-2,0)变为A(0,0),从而使直线方程变得简单.在与斜率有关的问题时,采用平移坐标系加齐次化的技巧,绕开一系列复杂的书写和消元.适当补充圆锥曲线常见结论,在高观点下解读相关问题.这些结论和解读虽无法直接使用,但可以为解题提供方向.如有了极点极线的相关知识,在处理某些定点问题时,学生就会知悉定点,有的放矢,从而不会过分担心自己的计算失误.
2.3 关注综合性问题,注重思想的渗透和核心素养提升
在平时训练过程中,合理设置综合性的问题.如函数的本质是一种对应,其与数列、方程、三角、不等式、解析几何之间都可以建立起良好的综合关系.而诸多解析几何的困难问题,都是以解析几何为载体,最终转化到函数问题.在知识的相似、趋同、承接、对比处合理综合,便于学生在各个知识间形成通路,促进各个知识的相互理解,构建知识的网状结构.如近年来热度倍增的双曲线问题,就可以和椭圆、抛物线形成良好对比.注重学科核心素养的提升,圆锥曲线问题是数学运算培养的良好模板,尤其是其提供了多个含参数的分式化简,便于学生反复练习并对比纠错.注重数学思想方法的渗透,如圆锥曲线和函数的结合的问题,可以十分清晰地感受到数形结合、转化、整体处理等思想方法.
参考文献
[1] 唐宜鐘.2020年高考圆锥曲线问题解法探索与备考建议[J].中学数学研究(华南师范大学版),2021(01):3-5.
[2] 2022年高考数学解答题解法荟萃[J].中学数学教学参考,2022(19):55-56.
作者简介 唐宜钟(1988—),男,陕西汉中人,中学一级教师;主要从事高中数学教学和竞赛研究.
