一种解耦式主动脚轮全向移动机器人的标定方法
2023-05-26邵兵兵叶国云郑天江许佳杰孙晨阳
邵兵兵, 叶国云, 郑天江, 李 齐, 许佳杰, 孙晨阳
一种解耦式主动脚轮全向移动机器人的标定方法
邵兵兵1,2, 叶国云3, 郑天江2*, 李 齐2, 许佳杰1,2, 孙晨阳2
(1.宁波大学 信息科学与工程学院, 浙江 宁波 315211; 2.中国科学院 宁波材料技术与工程研究所, 浙江 宁波 315201; 3.宁波如意股份有限公司, 浙江 宁波 315600)
由于机器人的加工制造和装配等因素引起的几何参数误差影响了运动学模型的准确性, 因此会同时降低运动控制和里程计精度. 为提升全向移动机器人的运动精度, 提出了一种针对基于解耦式主动脚轮的全向移动机器人的分步标定方法, 该方法通过限制关节空间运动输入来简化运动学矩阵, 并利用最小二乘法获得运动学参数的实际值, 从而提升运动学模型的精度. 搭建了基于解耦式主动脚轮的全向移动机器人实验平台, 并通过仿真和实验对标定算法进行验证, 实验结果显示在平面内三个自由度上速度控制精度和里程计精度均得到了显著提升, 证明了标定算法的有效性.
解耦式主动脚轮; 运动学标定; 分步标定; 运动控制; 里程计
全向移动机器人满足完全约束条件, 具有3个平面自由度, 机动性强, 移动灵活性高, 能够在平面上实现任意轨迹的运动, 因其独特的运动优势近年来被广泛应用于人类的生产和生活实践中[1-3]. 全向移动机器人主要有3种驱动轮: 麦克纳姆轮因其结构导致运动过程出现磨损和震动, 运动不平稳且效率低下; 球轮结构复杂, 且容易出现打滑; 主动万向脚轮因其结构优势, 运行更加平稳、高效, 更能满足全向移动机器人的运动需求[4-6].
运动的准确性是移动机器人实现路径规划、目标识别、同步定位与地图构建等功能的前提, 而里程计误差是影响运动精度的关键因素[7-8], 所以实现精准的运动控制以及高精度的里程计是十分重要的[9-10]. 在加工、制造和装配过程中引起的机器人几何参数名义值与真实值的不同而导致的几何误差[11], 对移动机器人的运动控制和里程计精度产生较大影响. 有效地降低里程计误差, 提高移动机器人运动精度是本文的研究重点.
当机器人在规则、平整、摩擦力足够的平面运动时, 机器人几何误差是里程计误差的重要来源[12],其中UMBmark方法是著名的两轮差速移动机器人系统误差校核方法[13], 国内外学者对其做出了许多应用和改进: Lee等[14]针对汽车式移动机器人改进了UMBmark方法, 通过直线和半圆的回路运动校准误差, 但没有考虑误差之间的耦合; Jung等[15]对UMBmark方法进行了扩展, 提出了一种新的校准方案并考虑了误差之间的耦合效应, 克服了传统UMBmark的局限性; 贝旭颖等[16]提出一种新的差速移动机器人几何误差校核方法, 综合考虑了误差来源, 误差模型更完善; 达兴鹏等[17]利用两个EKF对里程计系统误差和激光雷达安装误差迭代标定, 使误差收敛到真值, 但初次迭代的标称值是带有误差的; 卢纪凤等[18]对差速移动机器人通过UMBmark离线标定和EKF在线标定结合的方式校核系统误差. 上述学者提出的标定方法虽然不同程度地解决了差动平台的几何误差标定问题, 但对于全向移动机器人的几何误差标定研究较少, 且对于解耦式主动脚轮全向移动机器人而言, 其运动学矩阵复杂性更强, 具有更多的运动学参数且相互耦合, 无法应用上述方法解决.
为解决全向移动机器人几何误差标定问题, 本文针对基于解耦式主动脚轮的全向移动机器人提出了一种离线的分步标定方法, 通过限制关节空间运动输入减小耦合, 针对3个自由度参数设定了3种可提高标定精度的参考轨迹, 利用最小二乘法对简化的运动学矩阵进行线性回归求解, 然后对运动学模型进行补偿, 从而提升运动学模型的准确性.
1 解耦式主动脚轮全向移动机器人运动学分析
本文研究的全向移动机器人由4个具有驱动能力的解耦式主动脚轮驱动, 每个主动脚轮由滚动电机和转向电机同时驱动[19], 并且对称地安装在机器人的4个角上, 如图1所示.

图1 基于解耦式主动脚轮的全向移动机器人
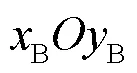
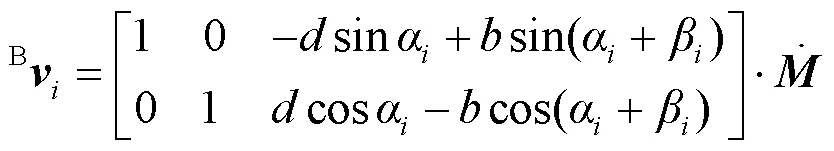
式中, , 和分别为机器人在基坐标系下沿x轴和y轴方向的速度, 为机器人绕z轴的角速度.
在脚轮坐标系下, 由脚轮的滚动速度和转向速度融合得到第个脚轮的轮心速度, 根据坐标系间的变换关系, 在基坐标系下表示为
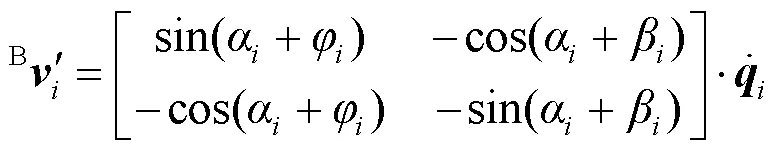
根据轮心速度相等, 联立式(1)和(2), 可得单个脚轮运动学关系:

式中,

由此可得全向移动机器人的整体运动学模型为
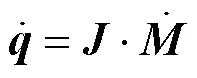
对上式进行分析后发现, 全向移动机器人运动学参数、、之间相互耦合, 其实际值与名义值的不同造成的几何误差严重影响着运动学矩阵的准确性. 根据全向移动机器人特点, 发现其在平面3个自由度上的运动是独立的, 因此可以通过分步的方法进行标定. 根据该方法, 设定3种标定轨迹来降低运动学矩阵的耦合度和复杂性, 实现运动学参数的标定, 从而达到提升运动控制和里程计精度的目的.
2 解耦式主动脚轮全向移动机器人标定算法
对于基于解耦式主动脚轮的全向移动机器人, 影响机器人运动的主要几何误差来源于脚轮的半径、脚轮的偏置以及脚轮的安装点距平台中心的距离. 平台共有4个驱动轮, 待确定的运动学参数有12个, 且相互之间存在耦合. 因此针对上述问题, 本文通过限制关节运动输入减少耦合, 设置了有利于提高标定精度的3种运动轨迹, 利用最小二乘法对简化的运动学矩阵进行参数辨识[24-25], 进而计算得到运动学参数标定值.
对算法推导、仿真以及实验中可能出现的参数约定见表1.

表1 标定参数
注:=1,2,3,4.
2.1 标定r
脚轮的半径和平台中心到脚轮的距离与脚轮的滚动运动相关, 且相互耦合. 脚轮的半径影响着机器人的平移运动, 因此首先协调好脚轮转角控制机器人进行直线运动, 利用工作空间速度与关节速度的对应关系, 对参数进行标定.
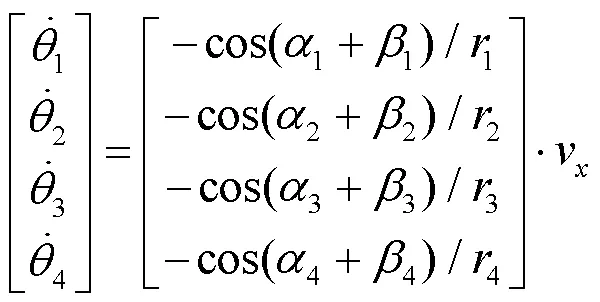
运用最小二乘法对上式运动学矩阵元素进行求解, 求解公式如下:
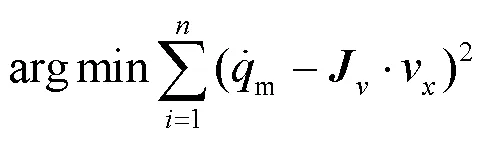
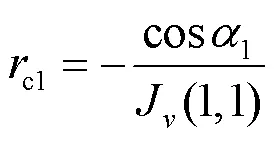
2.2 标定d
脚轮到平台中心的距离主要影响机器人的旋转运动, 协调脚轮转角, 控制全向移动机器人原地旋转, 利用关节速度与工作空间速度的对应关系, 对参数进行标定.
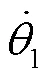
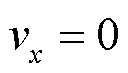
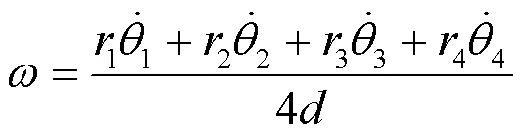
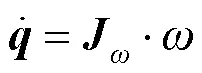
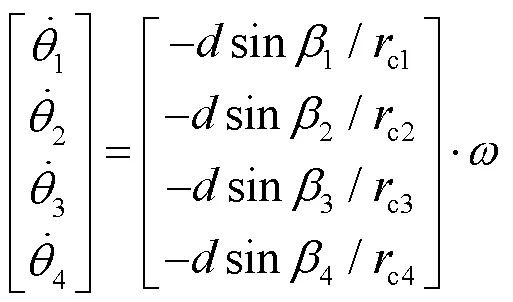
根据最小二乘公式辨识上式运动学矩阵元素, 具体公式如下:

2.3 标定b
脚轮的偏置与脚轮的转动运动相关, 若脚轮仅进行转向运动, 则会出现严重打滑, 因此设计一种姿态不变的圆形轨迹对参数进行标定.
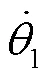

通过最小二乘法对上式参数进行辨识, 求解公式如下:
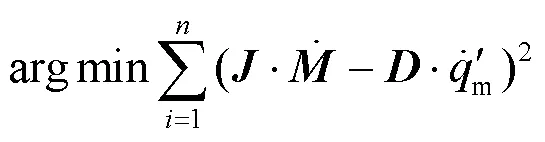
3 算法仿真
3.1 仿真过程
利用MATLAB等工具对上述全向移动机器人进行仿真实验.
在仿真环境中, 假设不存在打滑和传感器误差等非几何因素影响, 仿真模型中的运动学参数名义值为: 脚轮半径=55mm, 脚轮偏置=55mm, 脚轮到平台的安装距离=400mm. 给每一个运动学参数乘上一个误差比例系数, 得到的值作为仿真过程中的真实值, 由真实值计算得到的工作空间速度加入高斯白噪声, 作为工作空间的真实速度. 算法仿真流程如图3所示.
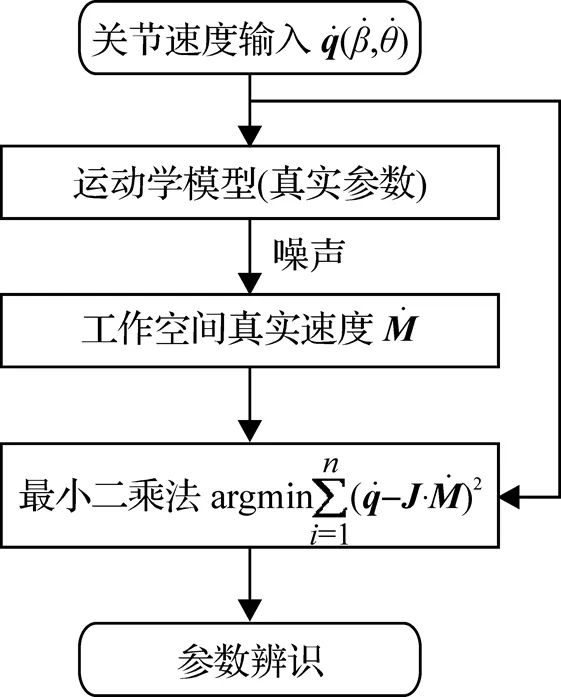
图3 标定算法仿真流程
3.2 仿真结果分析
对算法仿真的结果进行分析, 机器人的运动学参数名义值(加工制造的标称值)、真实值与标定值的结果对比情况见表2.
表2中误差1表示每个运动学参数名义值相对于真实值的差值绝对值, 误差2表示运用本算法标定后每个运动学参数的标定值相对于真实值的差值绝对值. 通过对比标定前后各参数与真实值的差值可以看出, 标定值更加接近真实值, 证明了标定算法可行性.
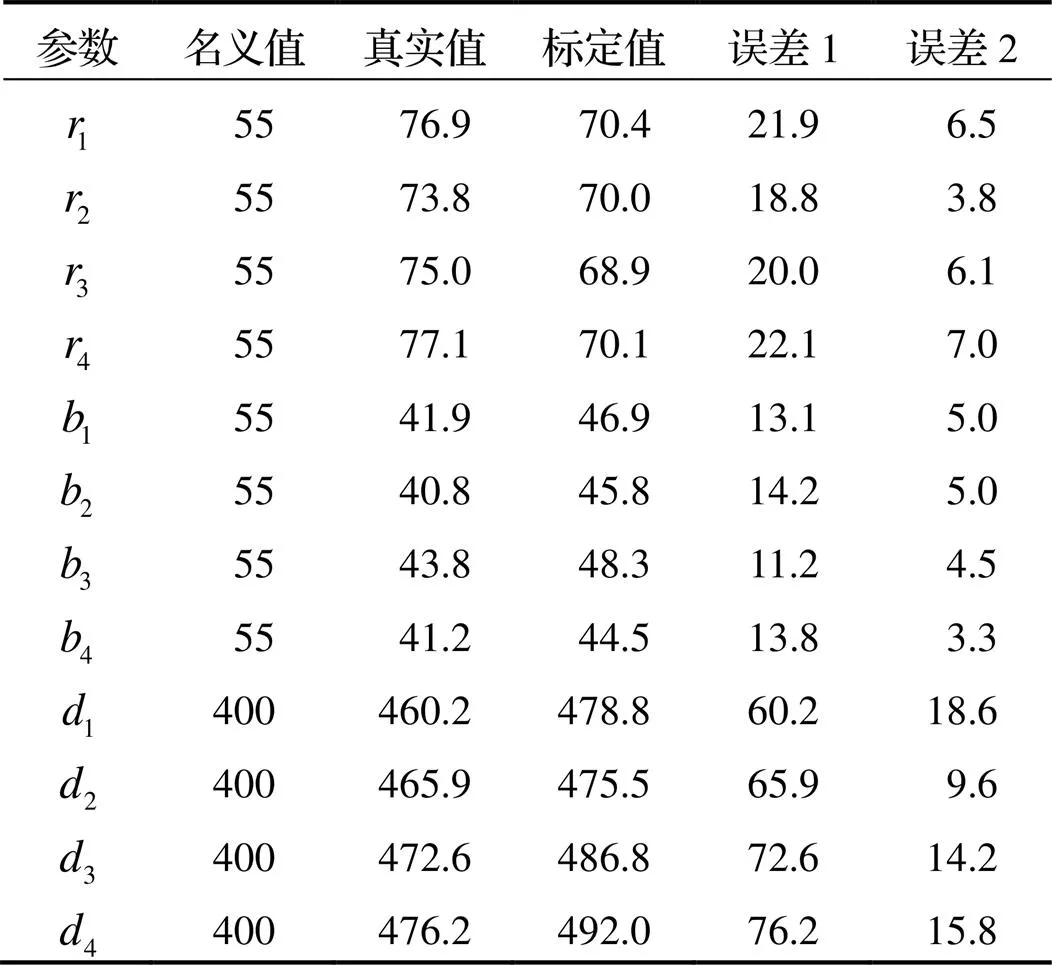
表2 标定参数仿真结果对比 mm
4 实验验证
利用解耦式主动脚轮全向移动机器人平台建立实验环境, 对标定算法进行验证, 并从机器人速度控制误差和里程计误差两个方面评价算法的有效性.
实验环境布置如图4所示, 实验设备由激光跟踪仪(Laser Tracker, LT)、全向移动机器人、上位机组成, 其中激光跟踪仪用于测量真实速度, 上位机向移动机器人发送命令, 控制全向移动机器人移动, 同时读取脚轮运动信息.

图4 实验平台
4.1 实验步骤
将标记小球放置在全向移动机器人中心, 将LT坐标系与全向移动机器人基坐标系进行拟合, 即可测量并计算得到移动机器人在基坐标系下的实际速度.
具体实验步骤为:
(1)通过上位机向关节空间发送运动命令, 控制移动机器人按照设计的轨迹进行运动;
(2)使用LT测量移动机器人工作空间实际速度, 同时在上位机中采集关节空间数据;
(3)将步骤(2)中计算的标定后的参数重新导入到上位机中;
(4)测量并比较标定前后的速度控制和里程计速度误差, 验证标定算法有效性.
4.2 实验数据分析
实验在平整、摩擦力足够的地面进行, 保证机器人平稳运行, 减小非几何因素影响, 实验场地足以满足全向移动机器人的运动. 实验中LT跟踪的机器人运动轨迹如图5所示, 图中箭头指向表示机器人运动过程中方向的朝向.
为验证标定后的运动学参数是否降低了误差, 定义平均速度误差, 表示为

分别将标定前后的运动学参数代入平台正逆运动学进行验证, 比较标定前后机器人速度控制和机器人里程计的误差.
工作空间真实速度相对于命令速度的误差对比结果如图6所示, 其中(a)~(c)依次为、方向的线速度误差和角速度误差. 标定前工作空间的速度控制平均误差为[0.021 0.024 0.026], 标定后工作空间的速度控制平均误差为[0.0036 0.0050 0.0041]. 对比以上数据可以发现速度控制误差在3个自由度上明显降低, 标定后的运动学参数有效提高了运动学矩阵的准确性, 从而显著提升了机器人的运动控制精度, 使机器人的运动更加接近真实状态.
图7为里程计解算速度相对于真实测量的工作空间速度的误差, 其中(a)~(c)分别为、方向线速度误差和角速度误差. 标定前里程计平均误差为[0.032 0.029 0.030], 标定后里程计平均误差为[0.0033 0.0028 0.0067], 里程计误差在3个自由度上显著降低. 通过对比分析以上数据发现标定后的运动学参数提高了运动学模型的精度, 同时里程计精度也得到了明显提升, 可以有效提高机器人定位精度.
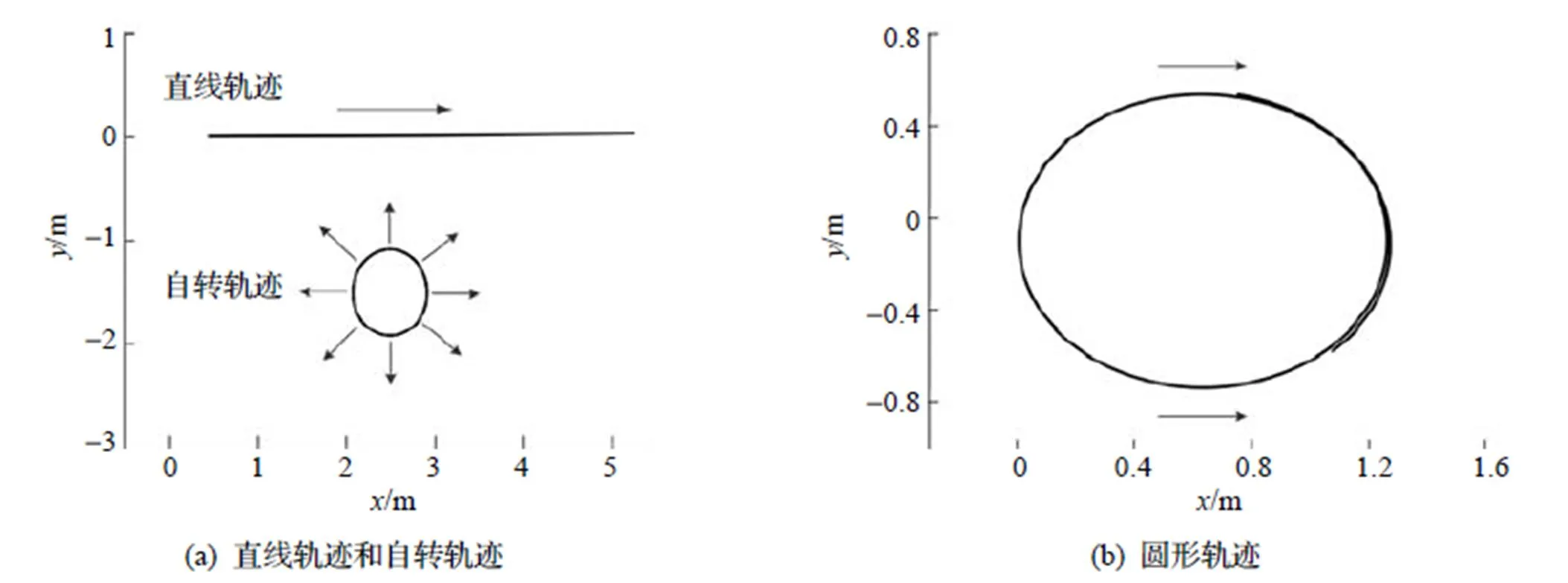
图5 LT跟踪的标定轨迹

图6 工作空间速度控制误差
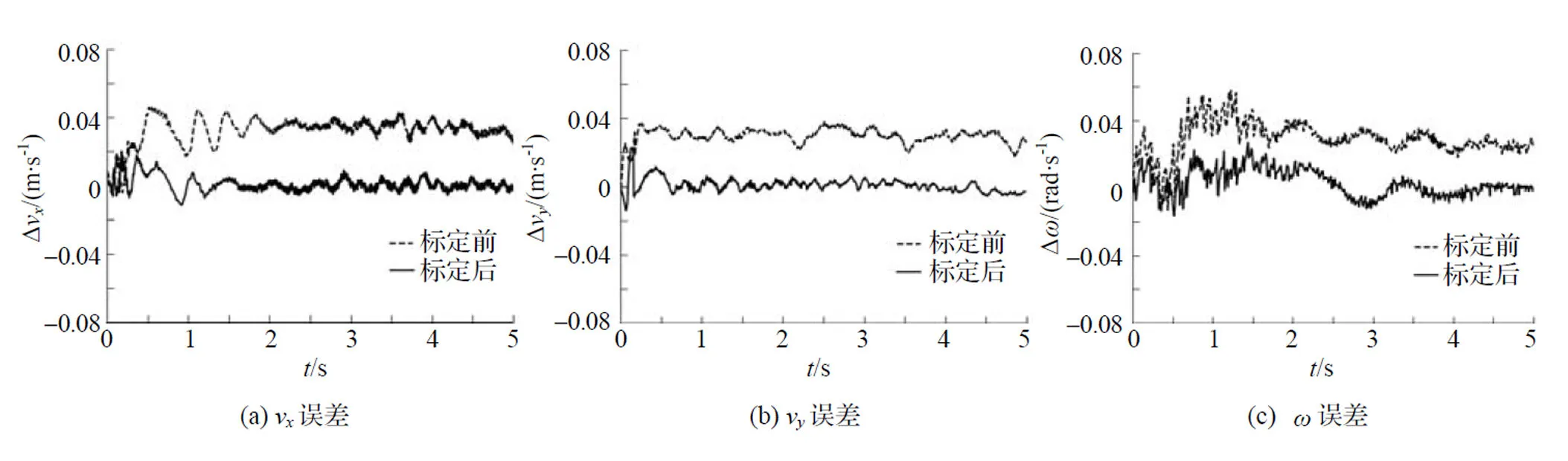
图7 里程计速度误差
5 结论
针对解耦式主动脚轮全向移动机器人运动学模型参数较多且耦合严重的问题, 提出了一种几何误差标定算法, 该算法通过限制关节空间运动输入, 分步标定运动学参数. 仿真结果显示, 标定后的运动学参数更加接近真实值, 运动学模型更加接近真实状态, 证明了该方法的可行性. 最后, 利用全向移动机器人平台进行实验, 对标定算法进行验证. 实验结果显示, 移动机器人的速度控制精度和里程计精度在平面3个方向(、方向的线速度和绕轴的角速度)上均得到了明显提升, 验证了方法的有效性. 后续工作将针对移动机器人与地面接触等不确定因素造成的非几何误差进行研究, 进一步提高机器人运动精度.
[1] Yin J, Yang G, Zhao F, et al. Motion planning implemented in ROS for omni-directional wheeled mobile robot[C]//2015 IEEE International Conference on Information and Automation, Lijiang, 2015:2695-2700.
[2] Wang J, Chen J. An adaptive sliding mode controller for four-wheeled omnidirectional mobile robot with input constraints[C]//2019 Chinese Control and Decision Conference (CCDC), Nanchang, 2019:5591-5596.
[3] 曲乃恒, 杨桂林, 郑天江. 基于解耦式主动万向脚轮的全向移动机器人设计[J]. 中国机械工程, 2015, 26(19): 2601-2605.
[4] Yang G L, Li Y P, Lim T M, et al. Decoupled powered caster wheel for omnidirectional mobile platforms[C]// 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, 2014:954-959.
[5] Kim D Y, Kim J H, Kim D. Development of an omni-directional mobile base utilizing spherical robots as wheels[C]//2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 2017:370-371.
[6] 李阳, 刘子明, 陈庆盈. 考虑打滑干扰的解耦式主动脚轮全向移动机器人跟踪控制[J]. 中国机械工程, 2020, 31(18):2247-2253.
[7] Xu H, Collins J J. Estimating the odometry error of a mobile robot by neural networks[C]//2009 International Conference on Machine Learning and Applications, Miami, USA, 2009:378-385.
[8] Tu Y, Min H. Calibration method of mecanum wheeled mobile robot odometer[C]//2019 Chinese Automation Congress (CAC), Hangzhou, 2019:3014-3019.
[9] Seong J, Jung D, Chung W. Odometry calibration for car-like mobile robots[C]//2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 2017:889-890.
[10] Fazekas M, Gáspár P, Németh B. Improving the wheel odometry calibration of self-driving vehicles via detection of faulty segments[C]//2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), Lyon, France, 2021:144-150.
[11] 王卫华, 熊有伦, 孙容磊. 测程法系统误差的测量与校核[J]. 机器人, 2004, 26(5):454-460.
[12] 张胜宾, 赵祚喜. 基于UMBmark算法的移动机器人定位试验研究[J]. 现代电子技术, 2018, 41(3):80-83; 87.
[13] Borenstein J, Feng L. Measurement and correction of systematic odometry errors in mobile robots[C]//IEEE Transactions on Robotics and Automation, IEEE, 1996: 869-880.
[14] Lee K, Chung W. Calibration of kinematic parameters of a car-like mobile robot to improve odometry accuracy [C]//2008 IEEE International Conference on Robotics and Automation, Pasadena, USA, 2008:2546-2551.
[15] Jung C, Chung W. Accurate calibration of two wheel differential mobile robots by using experimental heading errors[C]//2012 IEEE International Conference on Robotics and Automation, Saint Paul, USA, 2012:4533- 4538.
[16] 贝旭颖, 平雪良, 高文研. 轮式移动机器人里程计系统误差校核[J]. 计算机应用研究, 2018, 35(9):2696-2699; 2703.
[17] 达兴鹏, 曹其新, 王雯珊. 移动机器人里程计系统误差及激光雷达安装误差在线标定[J]. 机器人, 2017, 39(2): 205-213.
[18] 卢纪凤, 罗磊, 时轮. 基于UMBmark和EKF的差速移动机器人传感器系统误差标定方法[J]. 机械设计与研究, 2020, 36(4):149-153; 165.
[19] 王健. 主动脚轮式全向移动机器人的动力学解耦分析[J]. 机电信息, 2017(21):120-121.
[20] Afaghani A Y, Yuta S, Lee J H. Jacobian-matrix-based motion control of an omni-directional mobile robot with three active casters[C]//2011 IEEE/SICE International Symposium on System Integration (SII), Kyoto, Japans, 2011:627-633.
[21] Jia W, Yang G, Gu L, et al. Dynamics modelling of a mobile manipulator with powered castor wheels[C]//2017 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Ningbo, 2017:730-735.
[22] Zheng T, Zhang J, Wang W, et al. Design and control of two degree of freedom powered caster wheels based omni-directional robot[M]//Recent Advances in Intelligent Manufacturing, Singapore: Springer, 2018:568-580.
[23] Oetomo D, Li Y P, Ang M H. Omnidirectional mobile robots with powered caster wheels: design guidelines from kinematic isotropy analysis[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, Canada, 2005:3034-3039.
[24] Lin P, Liu D, Yang D, et al. Calibration for odometry of omnidirectional mobile robots based on kinematic correction[C]//2019 14th International Conference on Computer Science & Education (ICCSE), Toronto, Canada, 2019:139-144.
[25] Fazekas M, Gáspár P, Németh B. Parameter identification of the nonlinear wheel odometry model with batch least squares method[C]//2021 5th International Conference on Control and Fault-Tolerant Systems (SysTol), Saint- Raphael, France, 2021:360-365.
A calibration method for omnidirectional mobile robot based on decoupled powered caster wheels
SHAO Bingbing1,2, YE Guoyun3, ZHENG Tianjiang2*, LI Qi2, XU Jiajie1,2, SUN Chenyang2
( 1.Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China; 2.Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo 315201, China; 3.Ningbo Ruyi Co., Ltd., Ningbo 315600, China )
The accuracy of the kinematic model is affected by the error of geometric parameters caused by the machining and assembly of the robot, causing decline of the accuracy of the motion control and the odometry. In order to improve the motion accuracy of the omnidirectional mobile robot (OMR), a step-by-step calibration method is proposed for an omnidirectional mobile robot based on decoupled powered caster wheels (DPCW). This method simplifies the kinematic matrix by limiting the input of motion in joint space. Then the least squares method is used to obtain actual values of kinematic parameters. As a result, the precision of the kinematic model is improved. The experimental platform for the OMR based on DPCW is built, and the calibration algorithm is verified by simulation and experiment. The results show that the accuracies of both velocity control and odometry are significantly improved in three degrees of freedom in the plane, which proves the effectiveness of the calibration algorithm.
decoupled powered caster; kinematic calibration; step-by-step calibration; motion control; odometry
TP242.2
A
1001-5132(2023)03-0022-07
2022−10−11.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(U1509202); 浙江省自然科学基金(LD22E050007); 宁波市“科技创新2025”重大专项(2018B10069, 2021Z068, 2021Z020); 浙江省机器人与智能制造装备技术重点实验室(2015E10011).
邵兵兵(1997-), 男, 安徽亳州人, 在读硕士研究生, 主要研究方向: 移动机器人误差标定. E-mail: shaobingbing@nimte.ac.cn
通信作者:郑天江(1984-), 男, 湖南永州人, 高级工程师, 主要研究方向: 移动、软体机器人建模仿真及控制. E-mail: zhengtianjiang@nimte.ac.cn
(责任编辑 韩 超)
