基于分布式拍卖机制的多移动机器人动态任务分配算法

许佳杰, 陈思鲁, 张子栋, 邵兵兵, 刘 强, 张 驰, 杨桂林

基于分布式拍卖机制的多移动机器人动态任务分配算法

许佳杰1,2, 陈思鲁2*, 张子栋1,2, 邵兵兵1,2, 刘 强2, 张 驰2, 杨桂林2

（1.宁波大学 信息科学与工程学院, 浙江 宁波 315211; 2.中国科学院 宁波材料技术与工程研究所, 浙江 宁波 315201）

任务分配是多移动机器人调度系统的关键问题之一, 为了提高任务整体完成效率, 提出了一种基于分布式拍卖机制的多移动机器人动态任务分配算法. 该方法对机器人群体采用分布式控制方法, 彼此共享且动态更新任务集, 采用分布式的拍卖机制竞拍任务, 增加了调整任务执行顺序环节, 考虑任务整体完成效率, 最后在Linux系统下搭建了多机器人和障碍物的仿真环境. 结果表明, 该算法分配效率高于线性(CLP)算法和混合整数求解(CBC)算法, 且具有稳定性, 相比执行效率高的深度强化学习(DQN)算法和空缺链(VC)算法, 执行效率稳定, 移动代价降低了55％, 实现了较高执行效率和低移动代价之间的平衡, 可应用于实际仿真环境, 具有可行性.

多移动机器人调度系统; 动态任务分配; 拍卖机制; 分布式控制

随着智能制造时代的到来, 各类可移动机器人被广泛应用于各个领域, 随之配套的多移动机器人调度系统也显得举足轻重. 而任务分配算法是多移动机器人调度系统中的核心, 如何将任务分配给移动机器人, 使整个多移动机器人调度系统的效益最大化, 是多移动机器人任务分配领域亟待解决的问题[1]. 多移动机器人任务分配(Multi- Robot Task Allocation, MRTA)是机器人领域的核心问题之一, 是一个NP-hard问题, 主要分为两种类型: 第一种为Gerkey等[2]所提出的将其分为8种子类型; 第二种为Korsah等[3]提出的基于相互依赖的资源和约束, 将其分为4种子类型, 成为iTax分类. 任务分配策略根据相应的移动机器人应用进行分类, 主要分为基于拍卖任务分配策略和基于优化策略. 对实际任务分配环境的MRTA问题[4], 通常采用基于市场拍卖的任务分配策略来解决[5].

基于市场拍卖算法是一种突出的多移动机器人任务分配策略[6-8], 拍卖机制是其算法的核心. 启发式的遗传算法和拍卖算法的性能对比结果表明, 拍卖算法在分配问题上具有性能优势[9]. 近年来, 研究人员专注于开发针对复杂约束问题的动态任务分配策略和具有多种不确定性条件的鲁棒策略[10], 原因是传统的基于拍卖机制的任务分配方法面对动态场景时难以给出实时的分配方案, 失去了静态场景下的性能优势, 且鲁棒性差[11]. 基于市场的任务分配方法依赖于强连接的机器人网络, 其在沟通缺失或弱沟通环境下的任务完成率较差, 且局限于提高任务分配效率而不是任务整体完成效率[12-13]. 然而, 实际移动机器人任务分配场景不仅包括任务分配, 还包括任务执行; 而移动机器人运行状态决定了移动机器人是否能前往任务点执行任务[14].

本文提出了一种基于分布式拍卖机制的多移动机器人动态任务分配算法, 对移动机器人采用基于机器人操作系统(Robot Operating System, ROS)的分布式控制, 彼此共享且动态更新任务集, 采用分布式的拍卖机制竞拍任务, 根据移动机器人的状态信息确定移动代价最小的任务执行顺序, 实现了较高执行效率和低移动代价之间的平衡, 优化了任务分配结果, 提高了任务整体完成效率.

1 多移动机器人动态任务分配模型

1.1 多移动机器人任务分配定义

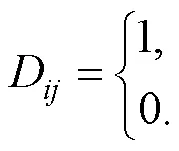
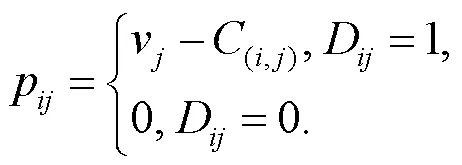
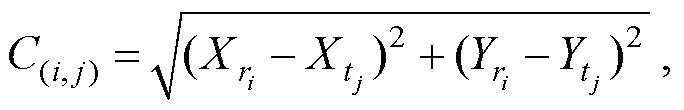
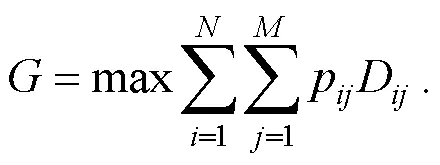
1.2 多移动机器人动态任务分配

多移动机器人的动态任务分配相比静态任务分配更适合应用在实际任务分配环境中. 以图1为例说明本文算法中动态任务的分配过程, 图1中方块为任务, 圆为移动机器人.

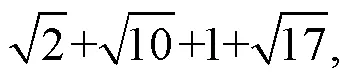
总收益最大为:

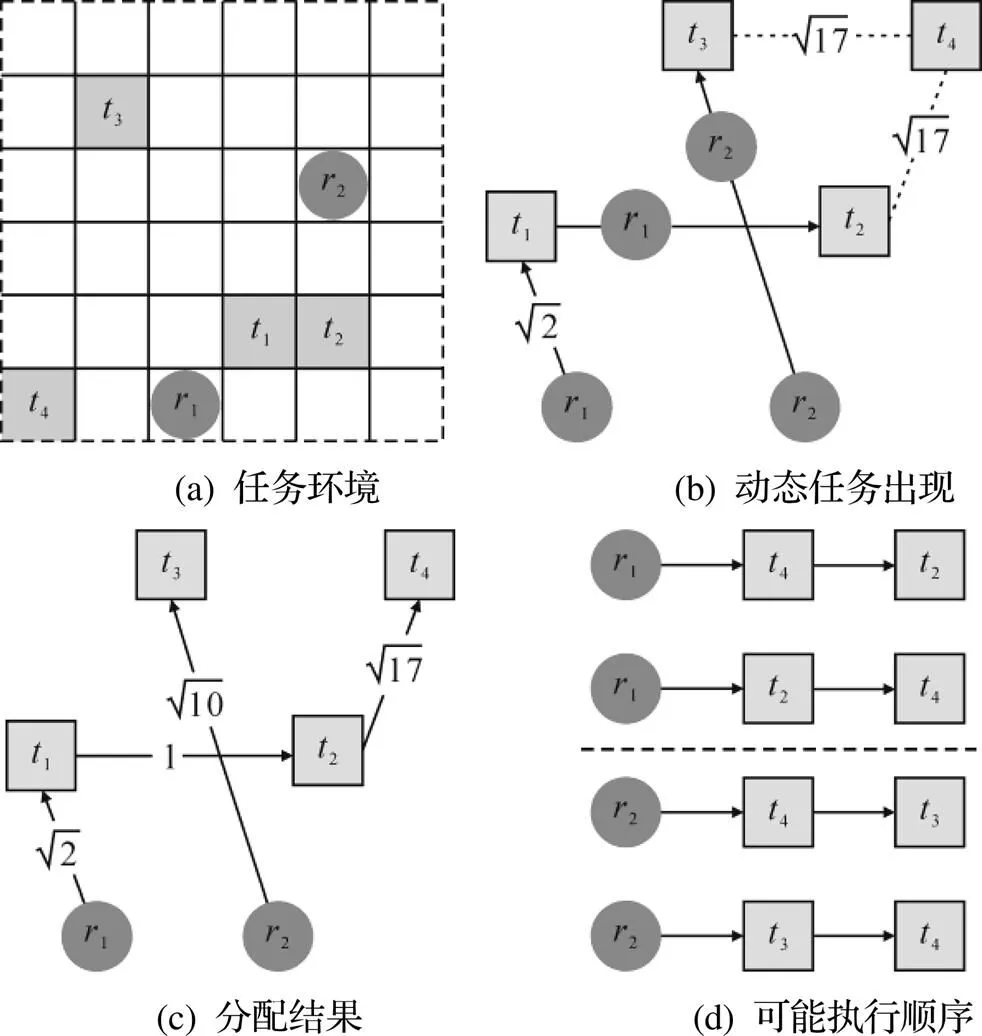
图1 多移动机器人动态任务分配过程

多移动机器人动态任务分配的目标是将动态变化的任务按照收益的大小合理地分配给每个移动机器人, 同时调整每个移动机器人的任务执行顺序, 最终使移动机器人完成所有任务后获得较好的任务收益, 使整个系统的总收益最大化.

2 基于分布式拍卖机制的多移动机器人动态任务分配算法设计

2.1 分布式拍卖机制的竞价与报价更新规则

ROS是一个分布式计算环境, 运行中ROS系统可以包含分布在多台计算机上的多个节点, 根据系统配置方式, 任何节点可以随时与任何其他节点进行通信. 对移动机器人采用基于ROS的分布式控制, 传统的集中式拍卖机制将转变为分布式拍卖机制, 不需要统一的调度中心进行任务分配, 移动机器人之间能够互相通信, 实现共享, 且实时更新任务集.

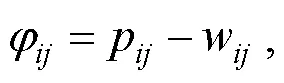
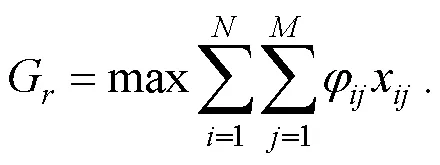
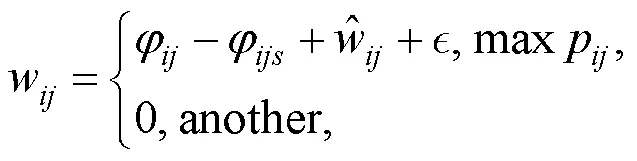
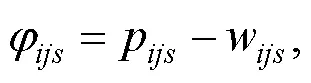
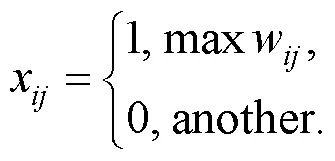
2.2 基于分布式拍卖机制的多移动机器人动态任务分配算法

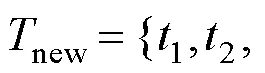
当任务分配过程中满足条件:

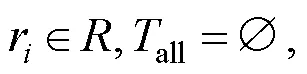
任务分配结束.

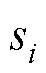
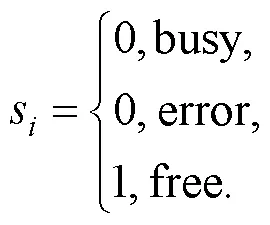
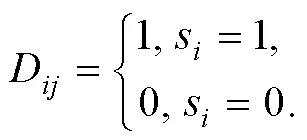
本文提出一种基于分布式拍卖机制的多移动机器人动态任务分配算法(Auctalgo算法), 具体执行通常可分为以下几个步骤:

(1)初始化: 统计所有待分配任务与机器人的相关信息(式(3)), 计算任务初始收益(式(2)), 移动机器人根据任务收益确定是否参与竞拍.

(2)竞价阶段: 机器人在确保自己利润最大化前提下对任务加价竞拍(式(7)), 如果任务当前价格大于预期利润, 则放弃竞拍(式(8)); 如果某个任务有最高出价的机器人出现, 报价将不再变动(式(9)).

(3)任务分配与执行阶段: 根据机器人的状态信息决定是否将任务分配给最高报价的机器人(式(12)), 如果被分配任务机器人无法执行任务(式(13)), 则由空闲最高报价机器人替代其执行任务, 并根据任务集确定移动代价最小的任务执行顺序.

(4)算法收敛条件: 如果总任务集为空集(式(11)), 算法停止; 否则进行新一轮分布式拍卖, 转向步骤1.

具体基于分布式拍卖机制的多移动机器人动态任务分配算法如下:

输出: 任务分配结果

1 初始化参数;

2 while 环境中还有未完成的任务do

11 else

12 跳出行4

13 end

14 else

15 跳出行4

16 end

23 计算任务执行顺序

24 end

28 计算任务执行顺序

29 else

32 end

33 end

34 end

35 end

3 结果与分析

3.1 算法分配效率比较

为了验证本文提出算法的分配效率、稳定性和可行性, 进行了仿真实验. 采用OR-Tools开源组合优化问题求解器中处理复杂分配问题的线性(CLP)和混合整数求解算法(CBC)[15]与Auctalgo算法进行分配效率对比.

移动机器人与任务数量比设定为1:1, 3种算法在不同数量移动机器人下的分配效率如图2(a)所示. 仿真结果表明, 当移动机器人数量超过300个时, CLP算法与CBC算法的分配效率骤降, Auctalgo算法的分配效率相对稳定. 为进一步探究算法的稳定性, 继续增加移动机器人数量来测试算法的分配效率, 最终结果如图2(b)所示. 从图2(b)可发现, 在移动机器人数量超过32000个后, 算法的分配时间才开始明显增加, 表明在面对众多数量移动机器人场景下Auctalgo算法稳定.

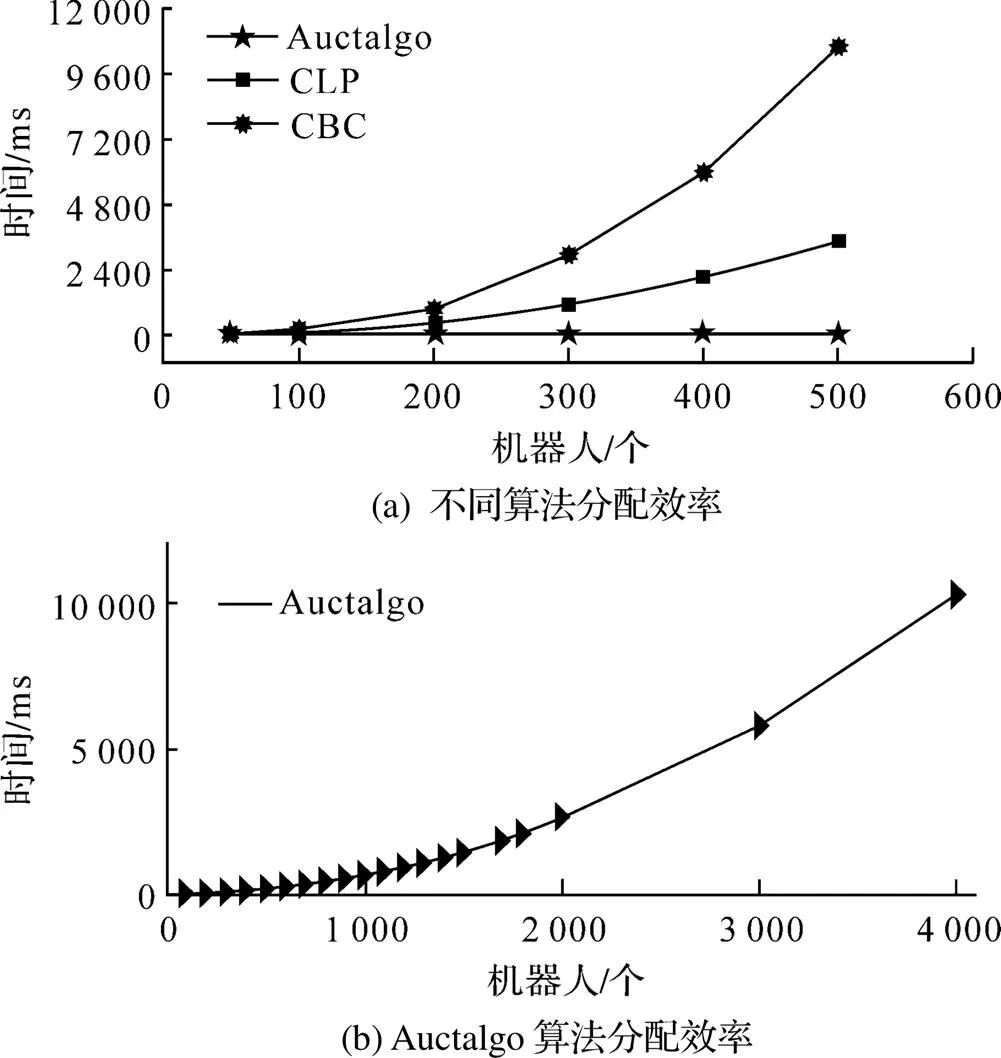
图2 算法分配效率

3.2 算法整体性能比较

实际任务分配场景包括任务的分配和执行, 因此算法的分配效率并不能决定任务整体完成的效率. 因此, 将从任务完成时间和移动代价两方面来评价算法的性能. 通过多移动机器人任务分配模拟系统进行仿真实验, 该系统基于ROS对移动机器人采用分布式控制, 接近真实环境[16]. 将算法与执行效率高的空缺链(VC)算法和深度强化学习(DQN)算法对比, 结果如图3所示.

图3(a)～(c)为拥有5个移动机器人和5个任务场景下任务分配结果, 图3(d)～(f)为拥有5个移动机器人和10个任务场景下任务分配结果. 为了减少方差并过滤掉随机影响, 每组算法进行8次. DQN、VC、Auctalgo 3种算法在任务完成时间上区别不大, DQN算法和VC算法在平均移动代价上分别为Auctalgo算法的1.9和1.8倍. 3种算法中DQN算法在任务完成时间上表现最差, VC算法在任务完成时间上比Auctalgo算法略有优势, 但DQN算法和VC算法在平均移动代价上分别为Auctalgo算法的2.5和2.2倍. 在任务数量增加情况下, Auctalgo算法在移动代价表现上优势明显, 实现了较高执行效率和低移动代价之间的平衡.

3.3 算法可行性分析

设计采用包含多移动机器人和障碍物的仿真环境来验证Auctalgo算法在实际任务分配场景下的可行性. 算法在Linux操作系统、内存为8G、基于ROS的move_base导航环境下运行. 仿真环境搭建和算法验证步骤如下: (1)创建基于激光雷达和IMU传感器导航的移动机器人统一机器人描述格式(URDF)模型, 然后在仿真平台Gazebo中加载模型, 最后设计包含3个移动机器人和障碍物信息的仿真环境, 借助机器人数据可视化工具Rviz可视化话题信息, 随机分配任务. (2)移动机器人群体采用基于ROS分布式控制, 彼此交换任务信息后, 最终算法给出整体无冲突, 且任务收益最大的任务分配方案. (3)移动机器人采集激光雷达和IMU数据, 并结合Move_base导航框架实现路径规划. 最终移动机器人根据算法调整任务执行顺序, 结合自身状态信息确认是否前往任务点执行任务.

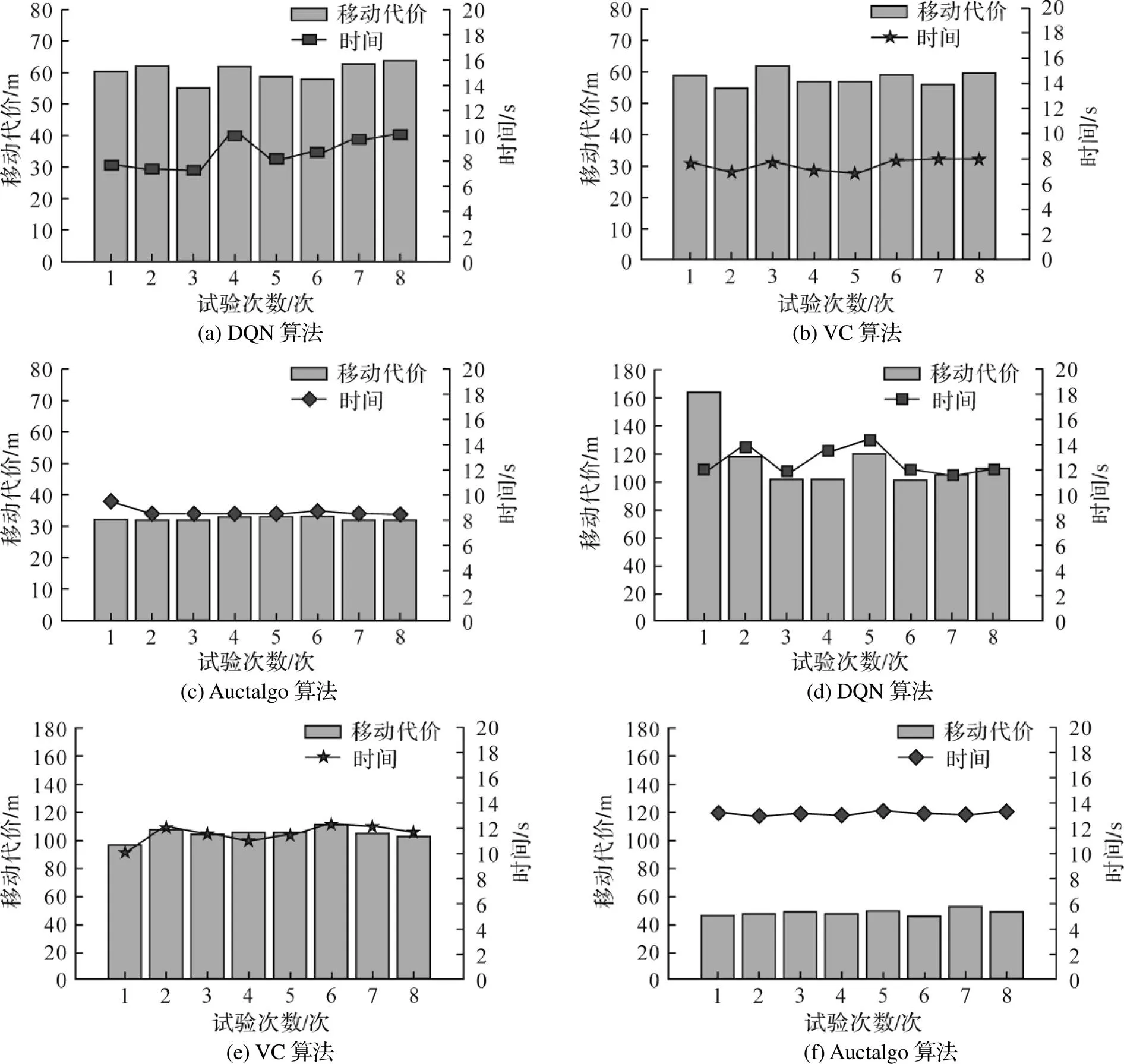
图3 不同算法任务分配结果

3个移动机器人分别前往任务点的移动代价见表1. 最终移动机器人A1竞拍到任务B1, 价格为8.35. 移动机器人A2竞拍到任务B3, 价格为7.18, 移动机器人A3竞拍到任务B2, 价格为8.21.

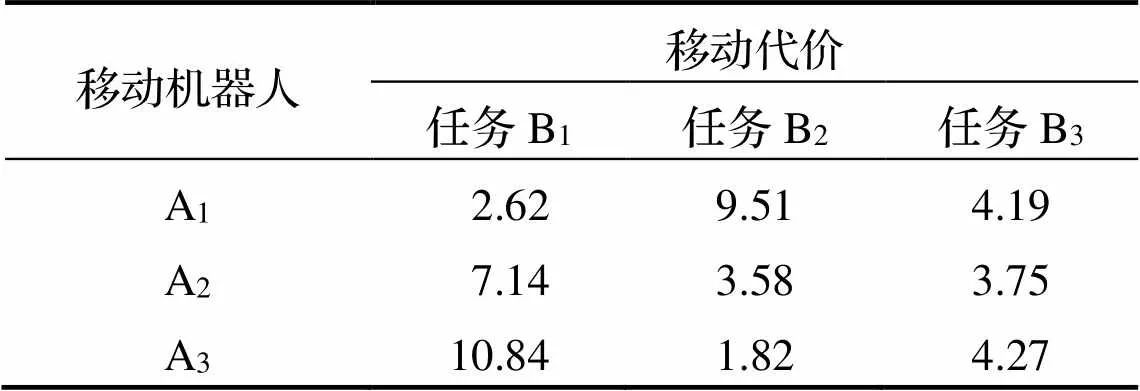
表1 移动代价

任务分配过程和结果如图4所示, 包含了3个移动机器人当前位姿和障碍物以及运行路径等信息. 最终移动机器人A1从当前点出发到达任务点B1, 移动机器人A2从当前点出发到达任务点B3, 移动机器人A3从当前点出发到达任务点B2. 当出现新任务时, 算法能进行实时任务分配使移动机器人最终完成任务执行. 仿真结果表明, 在分布式控制下, Auctalgo算法能够应用于多移动机器人任务分配的仿真环境, 成功实现任务的分配和执行, 验证了算法的可行性.

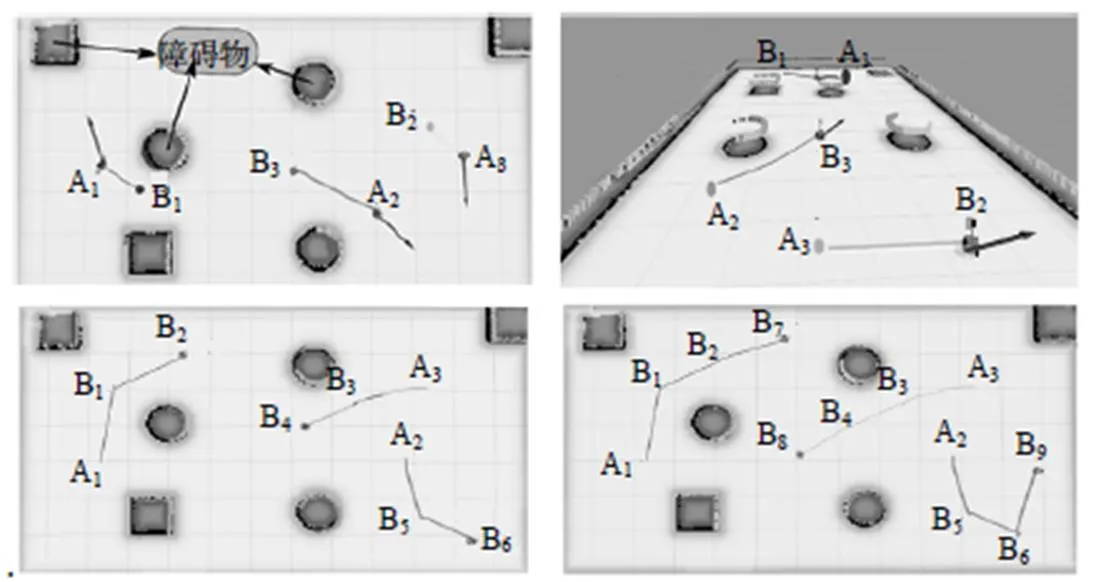
图4 不同任务数量下的任务分配结果

4 结语

本文针对传统拍卖算法的拍卖机制在动态任务分配场景下鲁棒性差、忽略任务整体完成效率、在弱沟通环境下任务分配完成率较差等问题, 提出了一种基于分布式拍卖机制的多移动机器人动态任务分配算法. 算法综合考虑机器人状态信息对任务完成的影响来评价任务分配整体效率, 增加了调整任务执行顺序环节, 实现了较高执行效率和低移动代价之间的平衡, 对动态任务分配场景有较强的鲁棒性, 显著提高了任务分配效率. 对移动机器人群体采用分布式控制方式, 不需要统一的调度中心分配任务, 彼此共享且实时更新任务集. 搭建了包含多移动机器人和障碍物的任务分配仿真环境进行仿真实验, 结果表明, 该算法分配效率高、稳定性强、具有可行性, 能解决多移动机器人动态任务的分配问题.

[1] D’Emidio M, Khan I. Multi-robot task allocation problem: Current trends and new ideas[EB/OL]. [2022-07-10]. https://ceur-ws.org/Vol-1949/ICTCSpaper07.pdf.

[2] Gerkey B P, Matarić M J. A formal analysis and taxonomy of task allocation in multi-robot systems[J]. The International Journal of Robotics Research, 2004, 23(9):939-954.

[3] Korsah G A, Stentz A, Dias M B. A comprehensive taxonomy for multi-robot task allocation[J]. The Inter- national Journal of Robotics Research, 2013, 32(12): 1495-1512.

[4] Tsang K F E, Ni Y Q, Wong C F R, et al. A novel warehouse multi-robot automation system with semi- complete and computationally efficient path planning and adaptive genetic task allocation algorithms[C]//2018 15th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 2018:1671- 1676.

[5] Luo L. Distributed algorithm design for constrained multirobot task assignment[EB/OL]. [2022-07-10]. https://www.ri.cmu.edu/pub_files/2014/8/Lingzhi_Luo_robotics_2014.pdf.

[6] 杨博, 王叶群, 黄国策, 等. 基于冲突分解的短波频点真实在线双拍卖算法[J]. 系统工程与电子技术, 2022, 44(9):2947-2954.

[7] Schneider E, Sklar E I, Parsons S. Mechanism selection for multi-robot task allocation[C]//Gao Y, Fallah S, Jin Y, et al. Annual Conference Towards Autonomous Robotic Systems, Cham: Springer, 2017:421-435.

[8] 郑阳超, 李珍妮. 面向资源最优分配的深度学习双边拍卖算法[EB/OL]. [2022-07-10]. https://www.doc88. com/p-39999494108107.html.

[9] Dai X F, Wang J Z, Zhao J Q. Research on multi-robot task allocation based on BP neural network optimized by genetic algorithm[C]//2018 5th International Conference on Information Science and Control Engineering (ICISCE), Zhengzhou, China, 2019:478-481.

[10] Sarkar C, Paul H S, Pal A. A scalable multi-robot task allocation algorithm[C]//2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 2018:5022-5027.

[11] Bertsekas D P. Auction algorithms for network flow problems: A tutorial introduction[J]. Computational Optimization and Applications, 1992, 1(1):7-66.

[12] Otte M, Kuhlman M J, Sofge D. Auctions for multi-robot task allocation in communication limited environments[J]. Autonomous Robots, 2020, 44(3/4):547-584.

[13] Whitbrook A, Meng Q G, Chung P W H. Addressing robustness in time-critical, distributed, task allocation algorithms[J]. Applied Intelligence, 2019, 49(1):1-15.

[14] Zhou X, Wang H M, Ding B, et al. Balanced connected task allocations for multi-robot systems: An exact flow-based integer program and an approximate tree-based genetic algorithm[J]. Expert Systems with Applications, 2019, 116:10-20.

[15] Menouer T, Le Cun B. A parallelization mixing OR- tools/gecode solvers on top of the bobpp framework [C]//2013 Eighth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing, Compiegne, France, 2013:242-246.

[16] Dai W, Lu H M, Xiao J H, et al. Multi-robot dynamic task allocation for exploration and destruction[J]. Journal of Intelligent & Robotic Systems, 2020, 98(2):455-479.

Dynamic task assignment algorithm for multi-mobile robots based on distributed auction mechanism

XU Jiajie1,2, CHEN Silu2*, ZHANG Zidong1,2, SHAO Bingbing1,2, LIU Qiang2, ZHANG Chi2, YANG Guilin2

( 1.Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China; 2.Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo 315201, China )

Task allocation is one of the key issues in multi-mobile robot scheduling system. The existing methods tend to focus on improving the efficiency of task assignment without considering the task execution time, ignoring the overall task completion efficiency and the computational cost. In addition, they usually adopt a centralized control architecture, which requires the robot to be in a stable and reliable communication environment. In order to solve the above problems, a distributed auction mechanism-based dynamic task assignment algorithm for multiple mobile robots is proposed. The method adopts a distributed control method for robot groups, shares and dynamically updates task sets with each other, bids for tasks using a distributed auction mechanism, adds a link to adjust the task execution order, and considers the overall task completion efficiency. Finally, a simulation environment with multiple robots and obstacles is built under Linux system and relevant experiments are conducted. The experimental results show that the algorithm has higher allocation efficiency than the linear and mixed integer solving algorithms CLP and CBC, and has stability. Comparing with the Deep Reinforcement Learning (DQN) and Vacancy Chain (VC) algorithms, the execution efficiency remains stable while the movement cost is significantly reduced by 55％, which achieves a balance between the efficiency and cost in operation. This study, as believed, can be put to the real-world applications with promising outlook.

multi-mobile robot scheduling system; dynamic task assignment; auction mechanism; distributed control

TP242.6

A

1001-5132（2023）03-0029-07

2022−09−21.

宁波大学学报（理工版）网址: http://journallg.nbu.edu.cn/

国家自然科学基金（U1509202）; 浙江省基础公益研究计划（LGG19E050007）; 浙江省机器人与智能制造装备技术重点实验室（2015E10011）; 宁波市“科技创新2025”重大专项（2018B10010, 2020Z020）.

许佳杰（1997－）, 男, 浙江杭州人, 在读硕士研究生, 主要研究方向: 多移动机器人调度. E-mail: xujiajie@nimte.ac.cn

通信作者:陈思鲁（1982－）, 男, 福建福州人, 研究员, 主要研究方向: 高速、高精度运动控制及工业自动化. E-mail: chensilu@nimte.ac.cn

（责任编辑 史小丽）