系统思考、多向整合，促进深度学习

胡海光

［摘 要］如何让学生真正学会用方程来解决问题，是简易方程单元教学的一大挑战。文章基于统整视角，在分析方程教学存在的问题后，从提前孕伏代数思想、把准单元教学主线、统整经验层面提出“实际问题与方程”的有效教学路径，以促进学生对方程的深度学习。

［关键词］统整视角；方程教学；深度学习

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）08-0051-04

一、问题的引出——代数思维VS方程思想

对于题目“五（1）班女生有30人，比男生人数的3倍少6人，男生有多少人？请列方程解答”，学生做错的极少，令人惊讶的是，有几个学生列出的方程是（30+6）÷x=3。笔者十分好奇，对其中一个学生进行了访谈。

笔者：能说说你列这个方程时的想法吗？

学生：女生有30人，比男生人数的3倍少6人，说明男生人数的3倍就恰好比女生的人数多6，所以30与6的和除以男生人数等于3。

笔者：你是根据“女生人数比男生人数的3倍少6人”来思考的。那根据这句话，你还能找到哪个等量关系？

学生（迟疑）：男生人数×3-6=女生人数。

笔者：根据这个等量关系能列方程吗？

学生：x×3-6=30。

可见，学生列不出教师所期望的方程，并非是列不出等量关系，而是习惯了算术思维，习惯了从问题出发来列算式，到最后一步再根据要求将其调整为方程的形式。这无疑与教学目标背道而驰。为什么学生学了这么多课时的方程知识后，方程思想还如此薄弱？教学究竟存在怎样的问题？又该如何改进？

二、原因分析——方程教学系统性思考的缺失

1.重视算术思维的训练，忽视方程思想的渗透

用方程解题与用算术方法解题，在思维方式上是不同的。算术的解题方式是通过一系列连续的运算，逐步展开面向结果的活动；方程的解题方式是发现各种量之间的关系，并把一个关系变成另一个等价关系的活动。从一年级到四年级，教师都是不断地强化算术思维，不断地训练学生搜寻信息解决问题的能力，使学生看到信息就将其与问题挂钩，看到等号就想求等号左边式子的运算结果。虽然教材早就编排了渗透方程思想的习题，如 “7+□=8、5+8=□+7”，但很多教师往往不够重视，对学生的方程思想的培养流于形式，久而久之，学生对方程思想感到极为陌生。因此，通过一个单元的教学以期改变并使得学生形成方程思想就是一个很大的挑战。

2.简易方程单元教学缺乏整体思考，零敲碎打，流于形式，疏于本质

在教学简易方程单元时，如果缺乏整体思考，就课论课，就会导致学生对概念本质的理解不深刻、单元核心内容不能深化。如“方程的意义”这一课，很多教师认为就是让学生知道“方程是含有未知数的等式”，因此在教学时都是给出一堆等式、不等式、有未知数或没有未知数的式子，让学生在分类辨别中认识方程。從形式到形式，教师教的也是形式化的方程，至于形式背后的深层含义——“方程应该是等号两边讲两个故事，两个故事的量相等，即含有未知的表示量相等的等式，其要点在于等量关系”（史宁中教授语），则往往不被教师察觉。这种忽视，使“方程的意义”的教学无法让学生充分体验量的相等关系与方程之间的本质联系，不能为后续“实际问题与方程”的教学做好充分的铺垫。

缺乏整体思考、整体设计的方程教学，只能就事论事，导致教学目标定位不准、教学合力不足。

三、教学对策——基于统整视角系统设计方程教学

1.纵向联系，理顺渗透目标

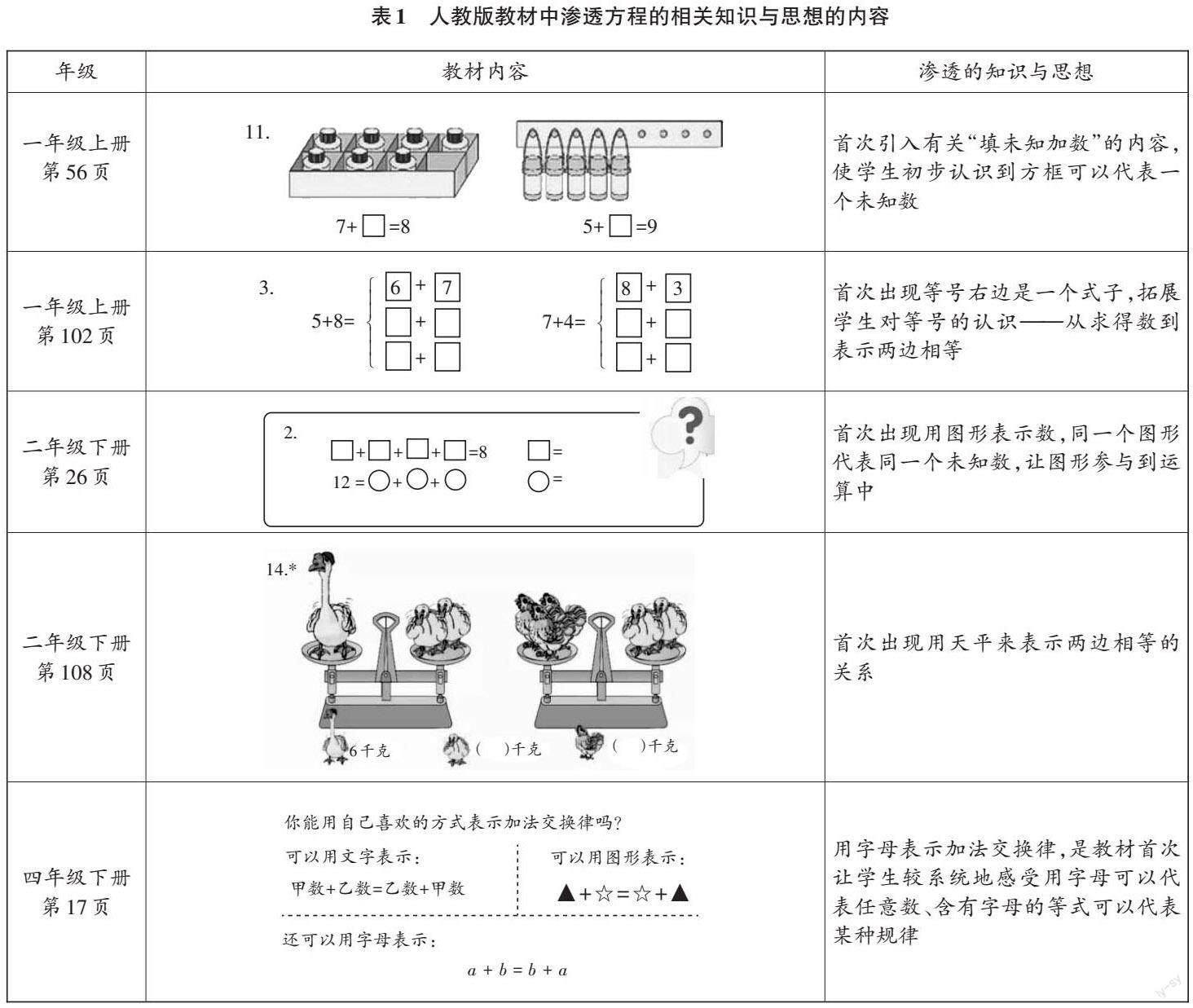
一种思想的形成并不是通过一个单元几课时的教学就能做到的，方程思想的形成亦是如此。人教版教材五年级上册的简易方程单元仅仅是方程知识、代数思想的集合，但人教版教材在编排时，早就有意识地在不同年级、不同知识领域渗透方程的相关知识与思想（见表1）。

从内容上看，教材中渗透的方程知识与思想呈螺旋式上升、由易到难之势。在一年级，教材更多的是用方框代表未知数，二年级下册则开始用图形□、○等代表未知数，到四年级下册就开始用字母代表任意数了。与方程相关的等式的含义、等量关系等也随着年级的升高逐步渗透。

从量上看，教材编排的方程知识与思想有着由多到少再到多的特点。在一年级上册中，根据低年级学生以顺向思维为主的特征，用方框代表未知数的次数相当多，共有10处，既为渗透方程思想，亦为学生逆向思维的培养奠定了思维基础。但到二、三年级，学生的逆向思维初步发展后，这种明显渗透代数思想的习题或内容显著减少，只有1、2处，到了四年级，数量又明显增加，尤其是在四年级下册，多达7、8处，但内容与一、二年级的差异较大，更多的是用字母代表未知数，抽象层次、符号化程度更高了。

顺应教材的编排特点，教师在教学时应统整教学目标，利用恰当的内容，寻找合适的时机，选择合理的方式，采取逐步渗透的方法，及时训练学生的代数思维与方程思想，为学生的长远发展奠定良好的基础。对于一年级上册第56页的第11题（见表1），可以让学生说一说“算式中的7是什么意思？8呢？这个方框里应填什么呢？”学生在教师的引导下能够得出“方框里的数表示拿走的个数，7个加上拿走的个数一共是8个”，初步感悟方程思想。对于二年级下册第26页第2题（见表1），则可以引导学生观察“□+□+□+□=8、12=○+○+○”后说一说这两个算式各自在讲一个怎样的故事，让学生认识到“这里的□、○各代表一个未知数，在同一个算式中□代表同一个数，4个相同的数加起来的和与8相等，同理，3个由○代表的相同的数的和与12相等”，最后通过问题“什么样的故事也可以用这样的算式表示？”进一步加深学生对方程思想的认识。对于四年级下册的加法交换律的教学，则让学生举例后思考：能否用一个式子表达你们想要表达的规律？在学生得出“a+b=b+a”时，追问：“这里的a、b表示什么？可以表示哪些数？这样表示有什么好处？”让学生感悟用字母可以表示数或用字母式可以表示规律，并感受用字母来表示的简洁性。这样有意识的、有层次的渗透，能让学生种下方程思想的种子，为后续学习方程的知识做足准备。

至于教材中很少安排或没有明显安排蕴含代数思想习题的二、三年级，有经验的教师会根据相关内容有意识地渗透方程思想。如对于三年级上册长方形与正方形单元的练习“请在格子图中画出周长是16厘米的长方形”，教师可通过追问周长16厘米是什么意思，引导学生得出式子“（    +    ）×2=16”，再让学生填一填、画一画。如在解决“小明有5元和2元面值的人民币各6张。如果要买一个30元的书包，有几种恰好付30元的方式？”时，除了用列表法，还可以引导学生用这样的方式来解决：（ ）×5+（ ）×2=30。学生在有序地解决问题的同时，学会思考解决问题的方法，在无形之中感受到方程思想的价值。

从整体目标出发，充分地利用教材，合理、有意识、按步骤渗透方程知识和思想，学生在学会算术思维的同时，自然受到代数思想的熏陶，这为后续学习方程的知识奠定坚实的基础。

2.横向梳理，明晰单元核心主线

一个单元知识点的编排，不仅仅是前后知识点的串联，更是数学思想的统一与贯穿。人教版教材五年级上册的简易方程单元一共分了两大板块：用字母表示数和解简易方程。解简易方程里又分了方程的意义、等式的性质、解方程、实际问题与方程这四小板块。从编排上可以看出，用字母表示数是解简易方程的准备部分，实际问题与方程实质是对方程的意义、等式的性质、解方程这几块内容的应用。基于这样的理解，简易方程单元本质是围绕“用方程解决实际问题”来编排知识点的，其核心是培养学生的代数思维与方程思想，使学生学会用建模（构建一个含有未知量的等式）来解决问题。

具体到各板块，“用字母表示数”是让学生更清晰地认识到含有字母的式子既可以表示一个数，又可以表示数量间的关系，强化学生用字母表示未知量的意识。如在进行基础练习后，可让学生通过完成习题“爸爸比小林大25岁。小林（）岁，爸爸（）岁”进一步明确小林的年龄不确定，可以用字母表示，比如a，因为爸爸比小林大25岁，所以可用“a+25”来表示爸爸的年龄。这样的教学不是死板地训练学生用字母表示数，而是在具体的问题情境中培养学生的代数思想。

“方程的意义”的教学应关注方程的本质，更强调方程的意义与现实中量的相等关系的对接，而非对单纯抽象的等式的归纳。广东省特级教师刘燕老师在教学“方程的意义”时，是这样处理的：

先出示，通过两个一年级小朋友小芳与小明引出两种算法“8-2=6、6+2=8”后，让学生进行解读。通过质疑小明的方法“6+2=8”——怎样让别人知道哪个数是答案？从而自然地得到“（）+2=8”，进而得出方程“x+2=8”。

再出示问题“盘子里原来有一些苹果，吃掉了7个，还剩3个，盘子里原来有多少个苹果？”分别用小芳和小明的方法来解决。由此得出“3+7=10、x-7=3”。

依次出示问题“爸爸今年36岁，小红年龄的3倍刚好和爸爸的年龄一样，小红今年多少岁？”“一个数加上31，再减去56等于320，这个数是多少？”“某风景区儿童票价格的2倍多5元，刚好是成人票的价格（145元）再加10元。儿童票的价格是多少元？”利用“小芳会怎么做？”“小明会怎么做？”这两个问题，引导学生分别得出方程“x×3=36、x+31-56=320、x×2+5=145+10”，与算式“36÷3=12、320+56-31=345、（145+10-5）÷2=75”。最后引导学生观察这些算式的异同，归纳方程的定义。

基于学生原有的经验，刘燕老师从一年级的看图解决问题开始，围绕实际问题的数量关系，把方程与等量关系巧妙地对接起来，凸显了方程的本质，渗透了方程思想，为后续教学“实际问题与方程”提供了知识与思想方法的准备。

让同一个单元的每一节课，都能围绕单元核心知识而展開，使每一节课都能成为单元核心知识网络中的一个重要部分，就能形成教学合力，从而促进学生深度学习。

3.统整经验，探寻有效教学路径

在小学数学的学习中，新知的学习都是建立在已有的知识基础与相关的学习经验上的。因此，统整学生相关的学习经验，帮助学生寻找对应的学习路径，能促进学生深度学习，从而提高教学的有效性。“实际问题与方程”这块内容是简易方程单元的最后一块内容，其本质是对前面“用字母表示数”“方程的意义”“等式的性质”“解简易方程”几个板块内容的应用。因此，根据学生的实际情况，整合其已有知识与经验，并在此基础上引导其学习，是有效达成“实际问题与方程”教学目标的关键。

如对于“实际问题与方程”例1和例2，可以这样处理：

（1） 唤醒经验，沟通联系

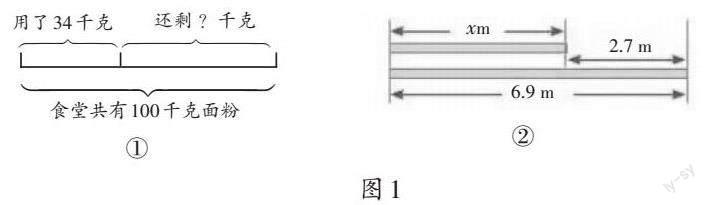
出示图1，要求学生看图列式或列方程。

预设：100-34=66（千克）， x+2.7=6.9。

设问1：x+2.7=6.9表示什么意思？

设问2：为什么第①题用算式，第②题却用方程？

追问：第①题也能像第②题那样列出方程吗？（把这个未知数看作字母x，可以列出方程）

小结：当数量之间有相等关系且含有未知数时，就可以列方程。

（2）丰富表象，积累经验

下列信息中，数量之间存在相等关系吗？能用方程表示吗？

①爸爸今年45岁，比小红大30岁。

②小王有72张邮票，是小红的3倍。

③小林买了1本练习本和3支价格为1.5元的水笔，共用去13.5元。

预设：45-x=30、x+30=45、45-30=x。

设问：这三个关系式都能表示小红和爸爸的年龄关系，哪个关系式最直白？

要求：请你用最直接、清晰的方程来表示第②、③题数量之间的相等关系。

引导比较：这里的列方程与我们以前看图列式计算有什么不同？

质疑：学会根据这些信息列出方程有什么用？

（3）运用经验，解决问题

出示：女生有60人，女生人数比男生的2倍多10人。男生有多少人？先独立完成，再交流；列方程或用算术方法都可以。

比较算术与方程的思维过程，让学生感受方程的价值和规范用方程解决问题的基本格式。

（4）巩固练习，提升经验（略）

首先，通过两个线段图，让学生回忆起已有的看图列式计算的经验；其次，借助这种经验，让学生尝试列出结构相同、未知数需用字母表示的方程，为后续的设未知数解题奠定基础；再次，出示含有等量关系的信息，让学生用方程表示，实质是预先排除问题对学生列方程的干扰，進一步调用学生已有的经验，强化学生根据实际信息列方程的能力，为解决实际问题搭建好脚手架；最后，通过解决实际问题，让学生在比较用算术方法解题与列方程解题的过程中，感受方程的价值，学会列方程解决问题的方法。这样的教学，基于学生的已有经验，让学生在经验的整合、改造中自然地获得知识和发展能力，进而构建良好的知识体系。

列方程解决问题对学生来说并不是全新的课题。在“用字母表示数”中，学生已经多次练习“根据数量关系列代数式”；在“方程的意义”中，学生则多次接触过“看图列方程”或“根据信息列方程”。显然，学生已有充足的根据等量关系列方程的经验。因此，在“实际问题与方程”的教学中，教师充分关注并整合学生已有的经验，让新知与旧知无缝衔接，就是促进学生的学习更有深度、更有效益的有效途径。

史宁中教授在《基本概念与运算法则》一书中谈到方程教学时强调，方程应该“先是进行生活中的提炼，然后到数学表达，再到形式化的过程，最后到解决方程问题”。这句话不仅指出了方程教学的实施路径，也从侧面反映了方程思想的培养不是通过一两节课就能实现的，它的实现依赖于系统的思考与安排、合理的统整与设计。

［ 参 考 文 献 ］

[1] 康克.凸显关键问题 促成意义建构：“列一步计算方程解决简单实际问题”教学设计与说明[J]. 小学数学教育. 2020 （Z2）：82-84.

[2] 吴雷霞.换种思路教“方程”：“实际问题与方程（1）”教学实践与反思[J].教学月刊小学版（数学），2015（Z2）：54-56.

[3] 张敏.“简易方程”单元教学思考[J]. 中小学数学（小学版），2019（Z2）：91-94.

（责编 金 铃）