液晶弹性体弹簧振子的周期性光驱振动行为及机理

2023-05-25胡少飞杜长慎

安徽建筑大学学报 2023年2期

李凯，胡少飞，杜长慎

（安徽建筑大学土木工程学院，安徽合肥 230601）

液晶弹性体（LCE）是一种由液晶单体和交联分子聚合形成的网络结构材料［1］。这种材料在热［2］、电场［3］、光［4，5］、磁场［6］或者化学物质［7］等信号的刺激下会发生变形，例如收缩［8］。这种刺激响应特性与肌肉遇到神经细胞信号时发生收缩非常相似。并且，LCE 具有响应快速、变形可完全恢复等优良特性，因而广泛应用于人工肌肉［9］、MEMS［10］、传感器［11］、能量采集器［12］、可拉伸光学器件［13］等领域。

在光驱动方面，LCE 的光驱动振动可以将光能转化为机械能，并用于软体机器人、微型工厂和纳米机器，而不需要传统的电动机驱动［14］。例如，紫外光［15］可诱导偶氮苯分子由反式变为顺式，并使LCE［16］发生较大变形。Finkelmann 等［17］合成了含偶氮苯分子的LCE，其光诱导收缩应变接近20%。White 等［18］实验研究了光敏液晶聚合物悬臂梁的振动，实现了激光作用下高频大振幅的振动。Torras 等［19］制备了含有碳纳米管的光致柱状弹性体悬臂梁，并研究了其弯曲动态响应。Li 等［20］基于LCE 动态模型建立LCE 悬臂梁动力学模型，理论研究了静态光源诱导的LCE 悬臂梁的自激弯曲振动。

有实验报道了一种超薄光响应LCE 纤维执行器，可以通过吸收环境中的光能补偿阻尼消耗的能量，在周期性光照下持续振动［21］。该实验表明，LCE 纤维的振动频率不仅取决于其本身的物理参数，还与外界周期性光照有关，且振幅随光照强度的增大而增大。该实验现象已被详细研究，但对此实验的理论分析还不够深入。

为了探讨周期性光照下LCE 弹簧振子的振动机理和行为，本文基于LCE 动力学模型，建立了LCE 弹簧振子的动力学模型，推导振子振动的控制方程，并数值求解振动的时程曲线。通过详细数值计算和分析，研究了光照周期和时间对振子振动周期、振幅和平衡位置的影响，并尝试找到一组对应最大振幅的最佳光照周期和光照时间。此外，还讨论了光强和阻尼等物理参数对振子振幅的影响规律。

1 模型及公式

1.1 LCE 弹簧振子的光驱振动控制方程

首先将一根原长为L0的LCE 纤维固定在固定端上，自由端连接一个质量为m的小球，此时LCE纤维的长度记为l，见图1。以LCE 纤维原长状态下末端的质点作为零点，建立位移坐标系，如图1（a）所示。在振动过程中小球的位移记为u（t），则LCE 纤维的瞬时长度l（t）可用小球的位移表示为l（t）=L0+u（t）。当处于光照状态时，纤维收缩，带动小球向上运动。当处于非光照状态时，LCE 纤维的变形恢复，在重力作用下，小球向下运动，周期性光照与系统振动的耦合可以触发稳定的强迫振动。

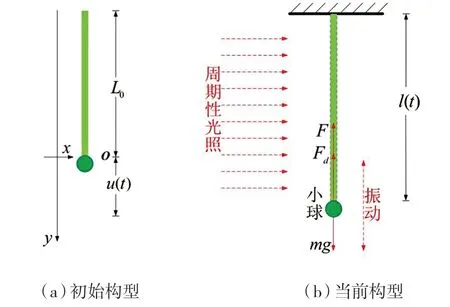
图1 LCE 弹簧振子示意图Fig.1 Diagram of LCE spring oscillator

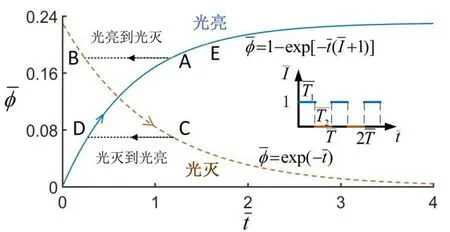
图2 周期性光照下，LCE 纤维顺式异构体数量分数随时间的演化规律Fig.2 Evolution law of number fraction of cis-isomers of LCE fibres over time under periodic light

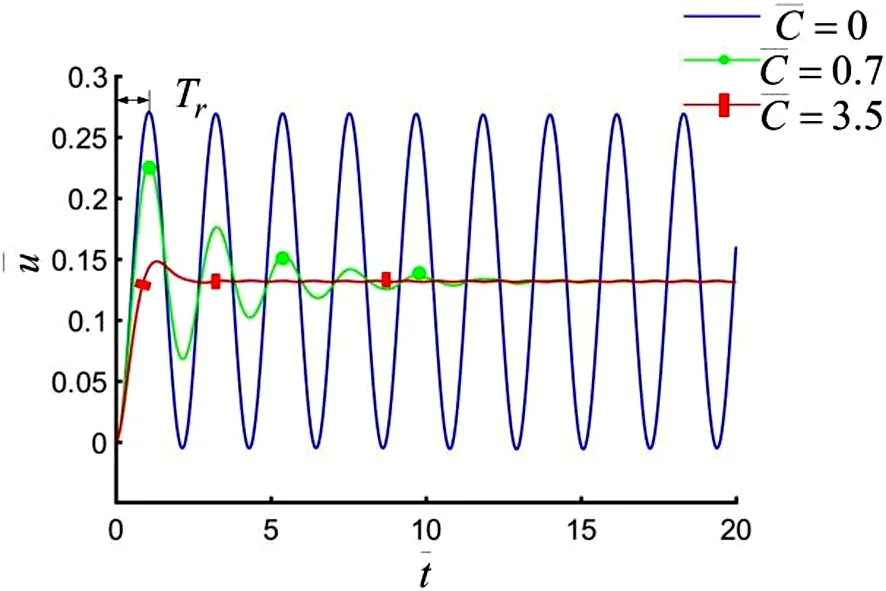
图3 连续光照下阻尼系数对弹簧振子振动的影响Fig.3 Effect of damping coefficient on spring oscillator vibration under continuous illumination

纤维的质量远小于小球质量，因此可忽略不计，见图1（b）。在整个过程中，小球受到纤维的拉力F（t）、自身重力mg和阻尼力Fd（t）。为计算简单，假设阻尼力与小球的速度成正比，且其方向与小球速度方向相反。根据牛顿第二定律，下面的控制方程适用于小球的振动：

其中，g为重力加速度，C为阻尼系数。

本文采用线弹性模型，LCE 纤维的弹簧力与变形成正比，公式（1）中纤维的拉力可以表示为：

其中，k为弹簧常数，假设光驱动的收缩应变ε（t）与LCE 纤维中顺式异构体的数量分数φ（t）呈线性关系，可以写为：

其中，α为收缩系数。

1.2 LCE 动力学模型

实验表明，波长小于400 nm 的紫外光或激光可以诱导反式到顺式异构化［22］。一般来说，在紫外光激发下，光驱动的顺式到反式异构化可以忽略，顺式异构体的数量分数φ（t）依赖于从反式到顺式的热激发、从顺式到反式的热驱动弛豫，以及光驱动的反式到顺式异构化。此外，相对于光驱动的激发，从反式到顺式的热激发通常可以忽略不计。本文利用下面的控制方程［23］来描述顺式异构体的数量分数φ（t）的演化：

其中，T0为从顺式状态到反式状态的热弛豫时间，I0为光强，η0为光吸附常数。求解方程（4）可以得到：

其中，φ0是顺式异构体的数量分数在t=0 的情况下。在光照状态下，初始顺式异构体分子数为零，即φ0=0，则公式（5）可以化简为：

在非光照状态下，即I0=0，公式（5）可以化简为：

在非光照状态下，将公式（8）写为无量纲形式：

1.3 顺式异构体分子数随时间的演化规律

1.4 无量纲化方程

1.5 求解方法

公式（12）和（13）是具有变因子的常微分方程，不存在解析解。本文利用经典的四阶龙格-库塔法方法，用Matlab 软件对常微分方程进行数值求解。首先将具有变因子的二阶常微分方程转化为两个具有变因子的一阶常微分方程。因此，控制方程被改写为：

四阶龙格-库塔法的公式为：

其中

在方程式中，h表示时间步长。通过迭代法得到LCE 弹簧振子的动态响应，即小球的位移和速度与时间的关系。

2 结果与讨论

2.1 无量纲参数取值

为研究LCE 弹簧振子的周期性运动，需对无量纲参数进行相应的估计。材料性能和几何参数见表1［23-25］。因此，可令无量纲阻尼系数为根据表中的无量纲典型值，分析LCE弹簧振动器C =CT0/m 。此时估计无量纲参数光强I为0.1。在周期性光照的振动现象。

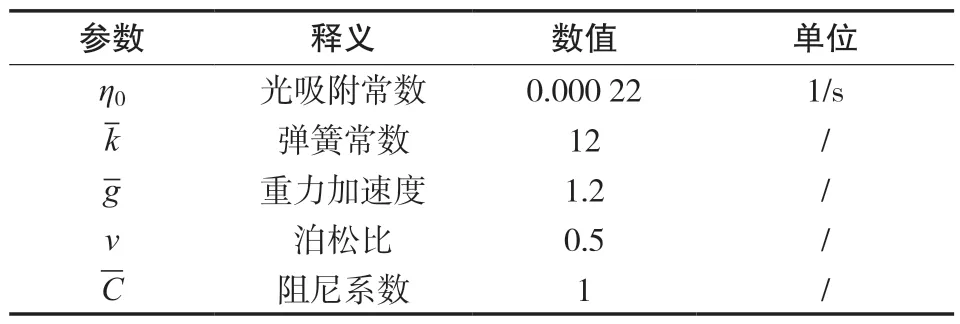
表1 材料性能和几何参数Tab.1 Material properties and geometrical parameters

2.2 连续光照下弹簧振子的振动

LCE 弹簧振子的连续光驱动振动是周期性光照的极限情形，在软体机器人主动控制方面尤为重要。为了反映发出和完成指令所需的时间，反应时间Tr可定义为从光照开始到目标变形的持续时间。下面主要讨论无量纲阻尼系数、无量纲光强对光束光诱导弹簧振子振动的影响。

2.2.1 阻尼系数对振动的影响

2.2.2 光强对振动的影响

在阻尼系数分别为C=0.7 和C=3.5 的条件下，光强对连续光照下弹簧振子振动的影响如图4 所示。从图4 可以看出，纤维位移u随阻尼的增大而减小；在相同阻尼条件下，纤维位移u随光强的增加而增大。但在整个过程中，反应时间不发生变化。

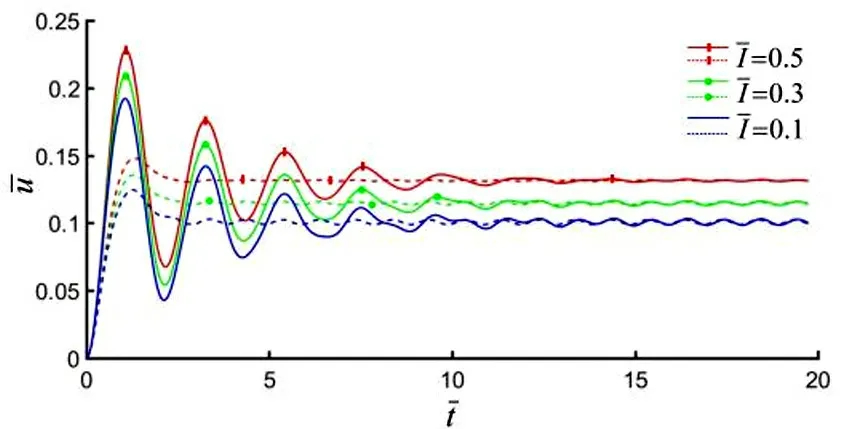
图4 连续光照下的光强对弹簧振子振动的影响Fig.4 Effect of light intensity on spring oscillator vibration under continuous illumination

由此可得，改变阻尼、光强会对位移产生影响。这些光驱动振动的特性可以用来指导光动力机器人的控制设计。

2.3 周期性光照下弹簧振子的强迫振动

周期性的光照是一种相对简单、常见的主动控制模式，因此掌握其控制规律尤为重要。弹簧振子的周期性振动在软体机器人和光-机械能转换系统中具有广泛的应用前景。下文以最大化弹簧振子的稳态振幅为标准，通过数值计算确定了最佳光照周期和最佳光照时间率。在达到最佳的周期光照模式后，分别研究光强、阻尼对振幅的影响。通过调节周期性光照、材料性能和几何参数，可以控制振动的振幅和周期。

2.3.1 最佳光照周期

在不同光照周期下，弹簧振子端部的强迫振动如图5 所示。在该系统中：C=0.7、I=0.1、g=1.2、k=12、T1/T=0.5。在此系统中，弹簧振子振动经过一段时间的非周期性振动后变为稳定的周期性振动。显然，弹簧振子振动起初由自由振动和纯强迫振动组成，由于存在振动阻尼，自由振动会消失，最终弹簧振子将只表现出纯强迫振动的稳定振动。由图5 可知，稳态的振动周期和光照周期保持一致，光照周期对振动的时间有很大影响。如图5（a）和（b）所示，当光照周期在自然周期的四倍内时，纤维振动呈现单峰稳态振动；如图5（c）和（d）所示，当光照周期是自然周期的四倍以上时，纤维振动呈现多峰稳态振动。多峰稳态振动相对复杂，文中不予讨论，下文仅讨论单峰稳态振动。为了方便起见，将振幅和平衡位置定义为（umax-umin）/2 和（umax+umin）/2，表达式中的umax和umin表示为稳态振动弹簧振子尖端振动位移的最大值和最小值。

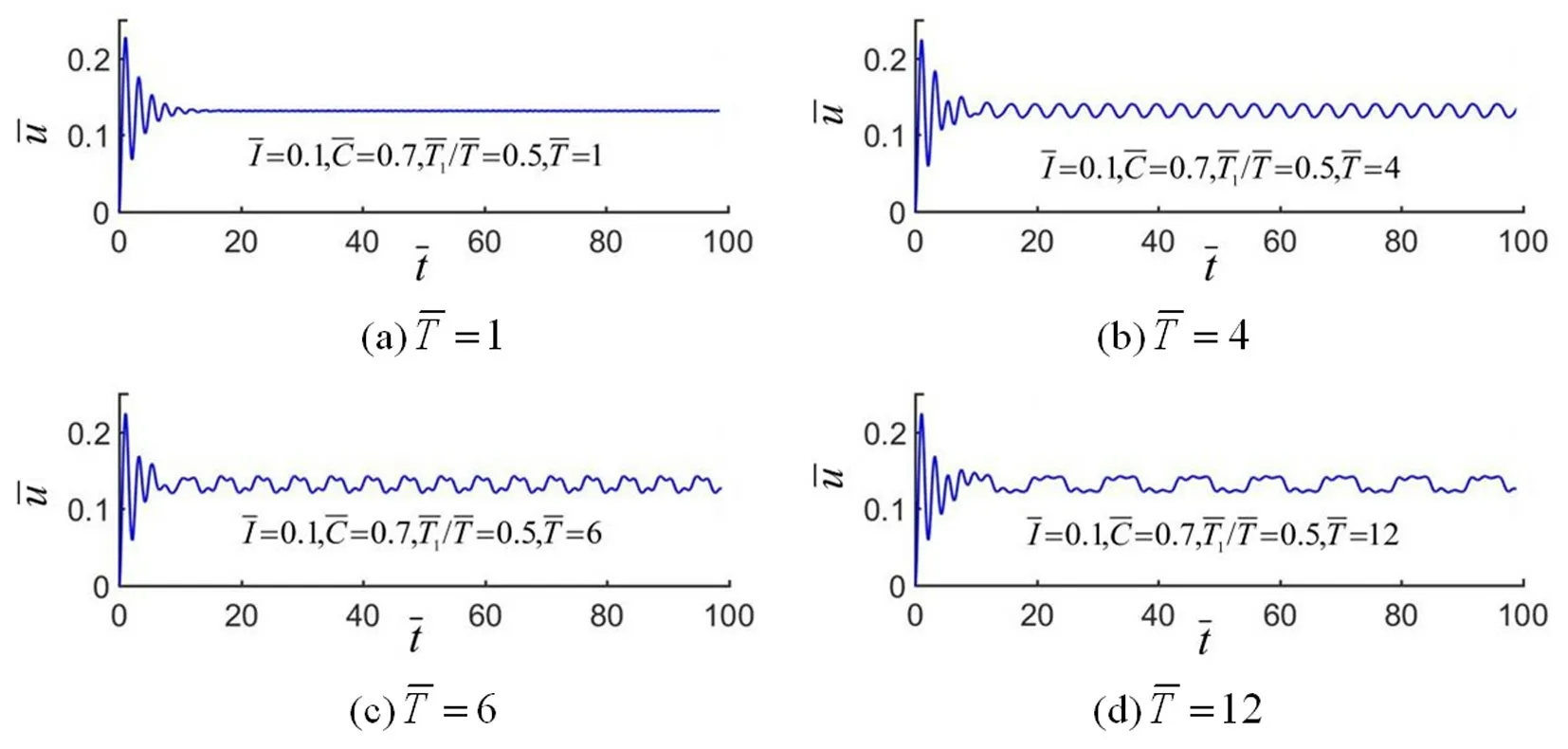
图5 周期性光照下，弹簧振子不同时期内的强迫振动Fig.5 Forced vibration of spring oscillator in different periods of periodic illumination

在不同的光照时间率下，弹簧振子端部的振幅随光照周期的变化如图6 所示。计算中确定：I=0.3、C=0.25、g=1.2、k=12。从图6 可以看出，随着光照周期的增加，整个弹簧振子振动的振幅先增加后减小，且在自然周期为1.82 时，弹簧振子振幅会达到最大值。这里需要注意，最佳光照周期不随光照时间率的改变而改变。

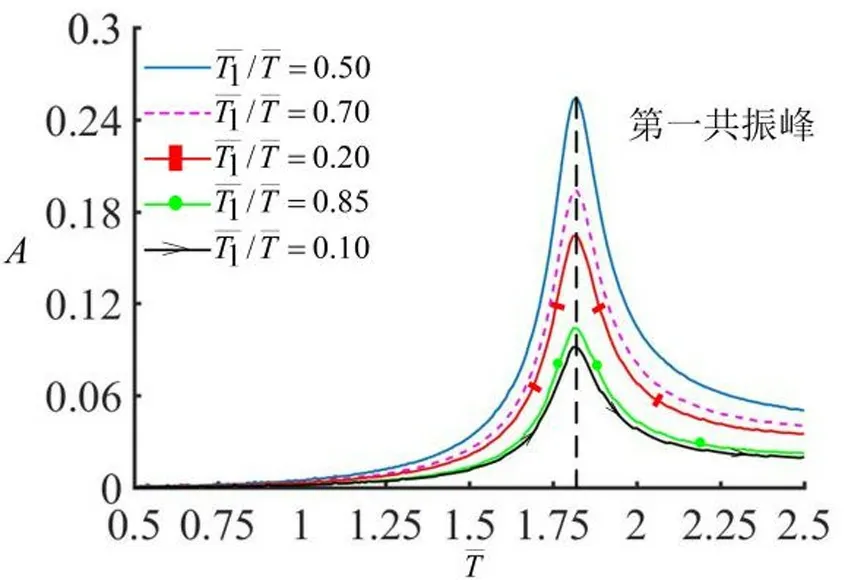
图6 在不同的光照时间率下，光照周期对弹簧振子端部振幅的影响Fig.6 Effect of light period on amplitude of spring oscillator with different illumination time rates

2.3.2 最佳光照时间率

弹簧振子振动振幅A和振幅平衡位置E随最佳光照时间率的变化规律如图7 所示，其参数：I=0.3、C=0.25、g=1.2、k=12。从图中可看出，弹簧振子振动平衡位置E和最佳光照时间率T1/T呈线性关系。当最佳光照时间率T1/T=0 时，振动平衡位置最大，这是第2.2 节中讨论的连续光照驱动振动的情况。

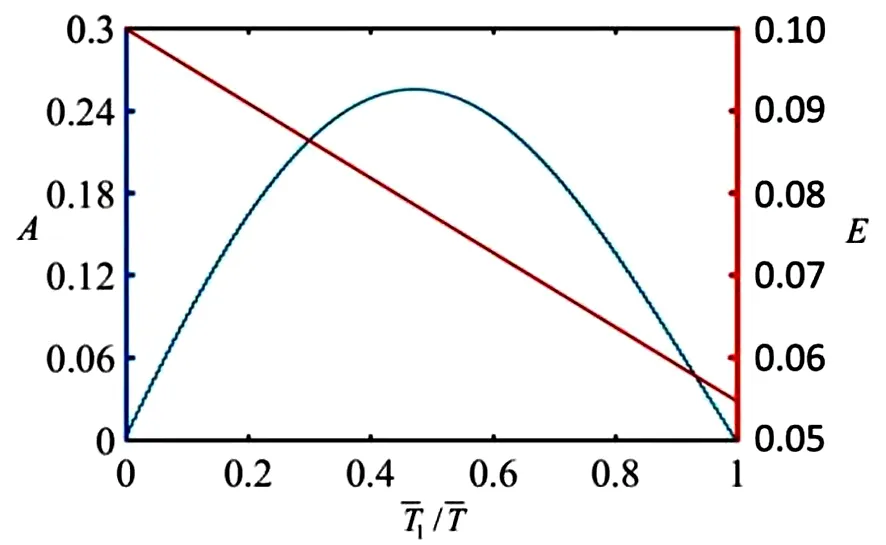
图7 弹簧振子振幅和振动平衡位置随最佳光照时间率的变化Fig.7 Variation of spring oscillator amplitude and vibration equilibrium position with optimum light time rate

从图7 还可看出，弹簧振子振幅关于时间速率点T1/T=0.5 对称，且在对称点T1/T=0.5 处时，弹簧振子振幅达到最大值。随着光照时间率的增加，弹簧振子振幅先增加后减小，且振动平衡位置向下作线性移动。因此，调节光照时间率可以控制软体机器人和能量采集系统的振动平衡位置和振幅。

2.3.3 光强对振动的影响

在不同光强条件下，弹簧振子端部振幅随时间的关系见图8。当系统处于最佳光照周期和最佳时间率的情况下，其参数为：C=0.25、T1/T=0.5、T=1.82、g=1.2、k=12。从图中可以看出，弹簧振子振幅随光照强度的增加而增加。这一理论预测结果与实验相符［21］。

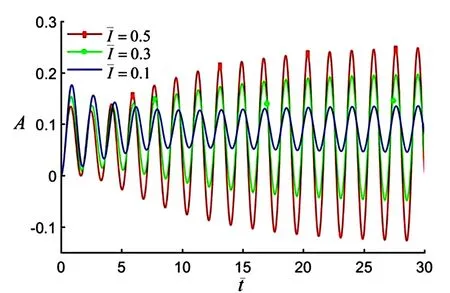
图8 在最佳光照周期和最佳时间率的情况下，不同光强对强迫振动振幅的影响Fig.8 Effect of different light intensities on forced vibration amplitudes with optimum light period and time rate

2.3.4 阻尼对振动的影响

在不同的阻尼系数下，光照周期对弹簧振子端部最大振幅的影响见图9。光强I=0.3，光照时间率T1/T=0.5。结果表明，该振动阻尼对振幅有很大影响。从图中可以看出，随着阻尼从0.7 增加到7，系统中弹簧振子振幅越来越小。这可以用能量守恒定律来解释：周期性光照提供光能，弹簧振子在振动的过程中吸收环境中的光能来补偿阻尼消耗的能量，稳定振动过程中，光能与阻尼耗散的能量相同。整个过程的能量守恒，当阻尼增大时，其消耗的能量也越多，则弹簧振子振动的能量越少，不可避免使弹簧振子产生的振动振幅减小。

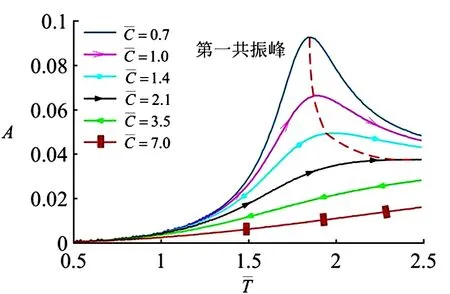
图9 不同阻尼系数下光照周期对LCE 弹簧振子最大振幅的影响Fig.9 Effect of light period on maximum amplitude of LCE spring oscillator for different damping coefficients

从图中可以得出，当光照周期远小于弹簧振子的固有周期时，振动振幅接近零，基本不受阻尼影响。当光照周期接近弹簧振子的固有周期时，阻尼会对振幅产生较大影响。当C=0.7 时，振幅达到0.092 57；当C=2.1 时，共振振幅仅为0.037 55；阻尼系数C大于3.5，不会发生共振。当光照周期远高于固有周期时，弹簧振子光驱动变形接近于2.2 部分讨论的连续光照驱动振动的情况。从图中还可以看出，随着阻尼的增大，固有周期也随之增大，如图中虚线所示。