基于到理想和非理想前沿线偏差的交叉效率评价

谭莹莹，郑婷婷，郭 冬

（安徽建筑大学 数理学院，安徽 合肥 230601）

当前对效率进行评价的主要方法包括投入产出法、模糊综合评价法、随机前沿法和数据包络分析法（Data Envelopment Analysis，DEA）。由于DEA 方法无须具体的生产函数形式、无须对数据进行量纲处理且无须预先主观设置权重，因此近年来取得了蓬勃发展并广泛应用于各类效率评价领域。

第一个DEA 模型，即CCR 模型，于1978 年由Charnes 等［1］首先提出。CCR 模型中效率为1 的决策单元（Decision Making Unit，DMU）处于有效前沿面上，被评价为有效的，效率小于1 的DMU 被认为是无效的。在CCR 模型下，每个DMU 都从自身效率最大化出发选取权重，获取的效率值可视为自评效率，结果一般导致多个DMU 被评价为有效，不能进一步有效区分。1986 年，Sexton 等［2］将自评效率和他评效率相结合，提出了交叉效率评价方法，有效提高了对各被评DMU 的辨析能力。

但由于自评效率中CCR 模型的最优权重通常不唯一，使得计算出的交叉效率具有随意性，很多学者建立了不同的第二目标模型解决这个问题。Doyle 等［3］提出了仁慈型和激进型交叉效率，通过最大化和最小化对同行的评价确定相应的权重和交叉效率值，进而可以对所有DMU 排序。Liang等［4］提出的博弈型交叉效率，在满足自我评价最大化的前提，尽可能最小化敌方的效率值同时最大化友方的效率值，以确定其交叉效率的权重。Wang 等［5］提出了中性交叉效率进行交叉效率评价，通过尽可能对自己有利，而不关心同行的想法确定相应的权重和交叉效率值，并给出相应的排序结果。李学文等［6］通过限制有效和非有效的DMU，改进传统的博弈交叉效率，利用施加全局限制的交叉效率模型确定权重和效率值，进一步获取排序。Shi 等［7］通过IDMU 和ADMU 定义了理想前沿与非理想前沿，利用其与理想前沿和非理想前沿的偏差确定权重，以获取交叉效率值和排序结果。Kao 等［8］将交叉评价的思想引入整体结构，对串联和并联结构的效率进行衡量，构建的模型将整体结构的交叉效率值分解为串联结构划分值的乘积和并联结构的加权平均，并在实例中进行交叉效率评价分析。Shi 等［9］在考虑有限理性行为下，将基于区间参考点的前景理论作为第二目标，以确定权重和交叉效率值，进而对14 家国际客运航空公司进行交叉效率分析。Zhu 等［10］提出了当被评价DMU 处于最优时，将公平理论引入交叉效率的模型以确定权重，并且提出了两种非线性模型的解决方法为所提模型求解。Zou 等［11］利用标准化的欧式距离定义判别幂和度量个体偏好与群体理想偏好的偏差度，由此提出比较交叉效率多个最优解的方法，并构建通用加权交叉效率模型以评价和排序。

通过理想决策单元（Ideal DMU，IDMU）和非理想决策单元（Anti-ideal DMU，ADMU）引入理想前沿线和非理想前沿线，进而最小化各DMU 与理想前沿线的最大距离，最大化各DMU 与非理想前沿线的最小距离以及最小化各DMU 与理想前沿线的最大距离的同时最大化它们与非理想前沿线的最小距离，以此设立第二目标确定投入产出权重和交叉效率值。利用建立的三类模型对14 家国际客运航空公司进行分析，并与传统交叉效率进行比较。

1 传统交叉效率评价方法

1.1 CCR 模型

设有n个被评价DMU，每个DMU 消耗m种不同投入，生产s种不同产出。记xij为第j个DMU的第i种投入，yrj为第j个DMU 的第r种产出。

1.2 传统交叉效率评价模型

可获得DMUk对DMUj的一个交叉效率，反映了DMUk对DMUj（j=1，2，…，n）的同行评价，即他评效率。DMUj的自评效率和（n-1）个交叉效率相结合可得DMUj的平均交叉效率，具体如表1所示。

表1 交叉效率表Tab.1 Cross-efficiency matrix

1.3 激进型交叉效率、仁慈型交叉效率和中性交叉效率

由于模型（1）通常有多个最优解，使得由（2）计算出的交叉效率具有随意性。为此，Doyle andGreen［3］提出了广为人知的激进型和仁慈型交叉效率模型：

其中，θkk*为模型（1）确定的DMUk自评的最优值。

模型（3）称为激进型交叉效率模型，DMUk在保持CCR 效率不变的情况下，最小化同行交叉效率；模型（4）称为仁慈型交叉效率模型，DMUk在保持CCR 效率不变的情形下，最大化同行交叉效率。

2010 年，Wang 等［5］认为DMU 有机会确定投入产出权重时，只会尽可能选择对自身有利的，不会过度在意对其他DMU 是仁慈还是激进。他们提出了一个最大化各产出效率的中性交叉效率模型：

2 基于理想前沿与非理想前沿的交叉效率

2.1 理性前沿与非理想前沿

和

2.2 基于到理想前沿和非理想前沿的距离偏差的交叉效率评价

2.2.1 基于到理想前沿偏差的交叉效率模型

设DMUj与理想前沿的偏差为dIj：

其中，θIDMU为模型（6）的最优解。

模型（8）中第一个限制条件是保持DMUk的CCR 最优效率，第二个限制条件是保持所有决策单元效率小于等于1，第三个限制条件是其他DMU与理想前沿线的距离小于最大偏差。模型（8）通过最小化其他DMU 与理想前沿线之间的最大距离，可确定唯一一组最优权重。

2.2.2 基于到非理想前沿偏差的交叉效率模型

⑭ The European Union，“Consolidated Versions of The Treaty on European Union and The Treaty on The Functioning of The European Union”，Official Journal of the European Union，Volume 53，C 83，p．91．

设DMUj与非理想前沿的偏差为dAj：

其中，θADMU为模型（6）的最优解。

模型（9）中第三个限制条件是其他DMU 与非理想前沿线的距离大于最小偏差。模型（9）通过最大化其他DMU 与非理想前沿线之间的最大距离，可确定唯一一组最优权重。

2.2.3 基于同时到理想前沿偏差和和非理想前沿偏差的交叉效率（以下简称基于二者）

当同时以理想前沿线和非理想前沿线作为评价标准时，保持被评DMUk满足CCR 最优效率，要求其他DMU 到理想前沿线的偏差越小越好，同时到非理想前沿线的偏差越大越好。由此建立如下模型：

模型（10）中第三个限制条件是其他DMU 与理想前沿线的距离小于最大偏差，第四个限制条件是其他DMU与非理想前沿线的距离大于最小偏差。模型（10）通过最小化其他DMU 与理想前沿线之间距离的同时，最大化其他DMU 与非理想前沿线之间的最大距离，可确定唯一一组最优权重。

3 实例

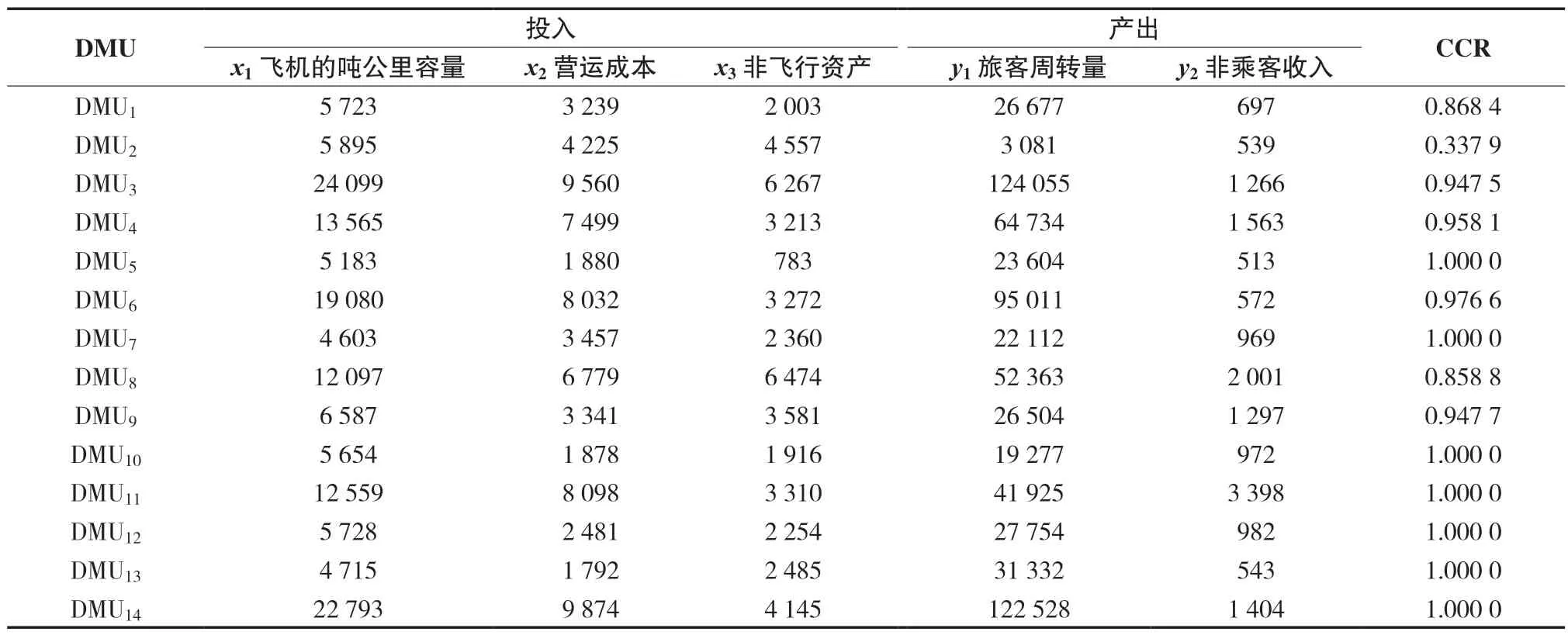
表2 14 家国际客运航空公司的投入、产出和CCR 效率值Tab.2 Input，output and CCR efficiency of 14 international passenger airlines

表3、表4 和 表5 分 别 为 基 于IDMU、基 于ADMU 和基于二者三类交叉效率模型确定的权重。

表3 基于IDMU 模型确定的权重Tab.3 Weights based on IDMU model

表4 基于ADMU 模型确定的权重Tab.4 Weights based on ADMU model

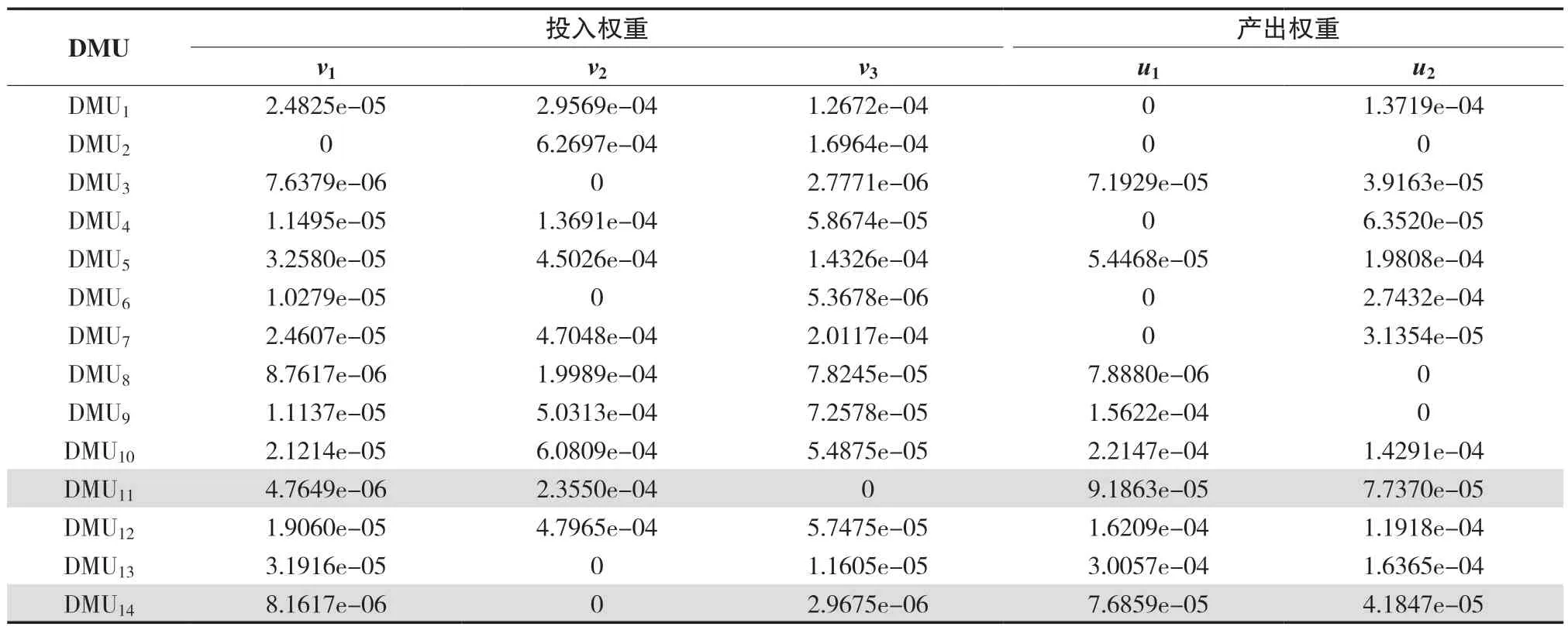
表5 基于二者模型确定的权重Tab.5 Weights based on IDMU and ADMU models

由三个表可以看出，一部分DMU 的权重在三类模型中是相同的，如DMU1，但是另一部分DMU的权重在三类模型中是不同的：对于DMU5，在基于IDMU 和基于ADMU 两个模型中的权重存在差异；对于DMU11，在基于ADMU 和基于二者两个模型中的权重存在差异；对于DMU14，在三类模型中权重各不相同。

表6 为本文所提三类交叉效率评价方法和经典的交叉效率评价方法对14 家国际客运航空公司评价的效率值。其中，经典交叉效率为激进型交叉效率、仁慈型交叉效率［3］和由Wang 等［5］提出的中性交叉效率。

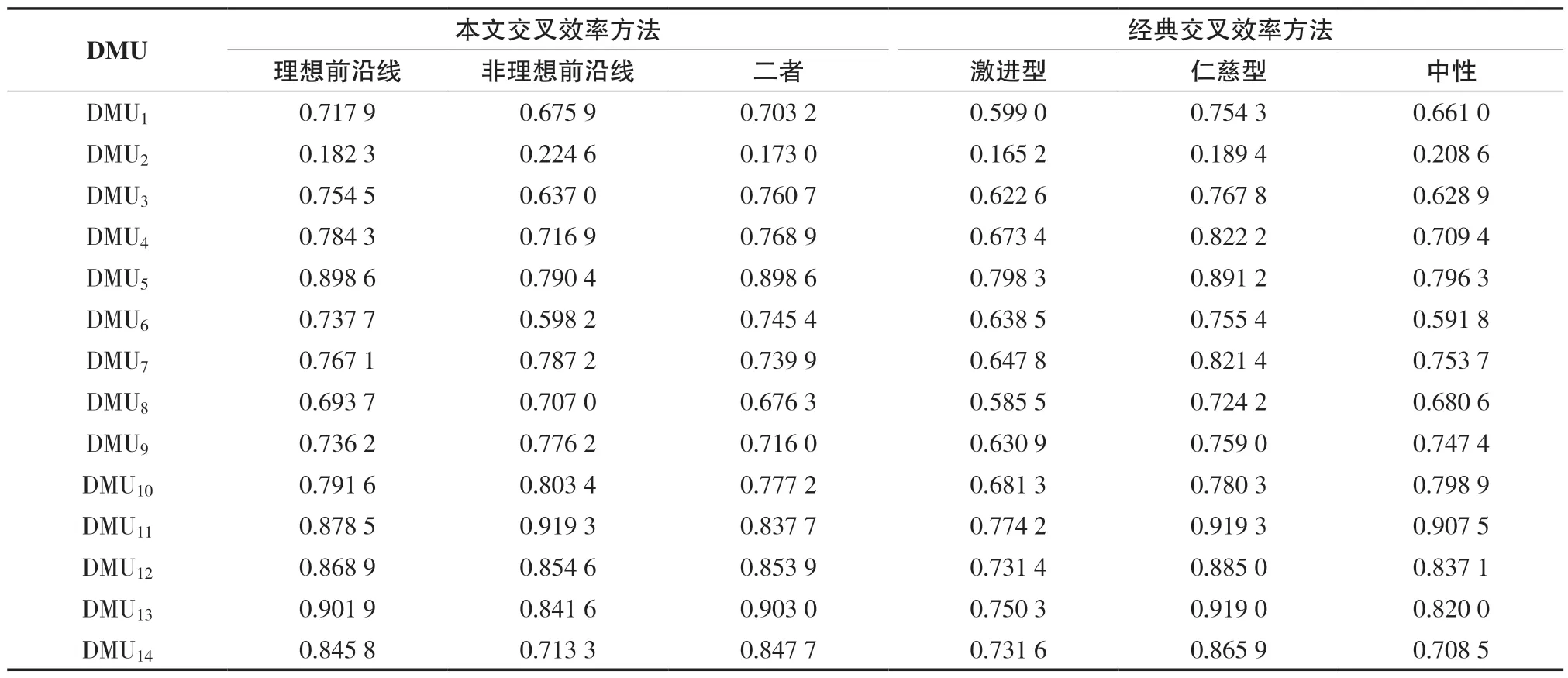
表6 本文交叉效率值和激进型、仁慈型、中性交叉效率值Tab.6 Cross-efficiency value of this paper and aggressive，benevolent and neutral cross-efficiency values

表6 中第二列至第四列为本文交叉效率值由模型（8）、（9）和（10）所得，第五列和第六列是由模型（3）、（4）和（5）所得。由表6 看出本文交叉效率评价方法中，基于二者模型的效率值处于基于理想前沿与基于非理想前沿两个效率值之间，在经典交叉效率评价方法中，中性交叉效率处于激进型和仁慈型效率值之间，且所有模型中最小效率均为DMU2。

图1显示的是表6中第二列至第七列的效率值。由图1 可观察到，三类模型的效率值在激进型和仁慈型的效率之间，且五个模型的效率比较接近，差异不大，而在DMU7至DMU13中，其他四个模型的效率值与激进型效率值之间差距相对较大。

图1 本文交叉效率值和激进型、仁慈型、中性交叉效率值Fig.1 Cross-efficiency value of this paper and aggressive,benevolent, neutral cross-efficiency values

基于理想前沿和基于二者两个模型与基于非理想前沿和中性交叉效率两个模型在DMU3至DMU6的效率存在较为明显的差距，其余的DMU之间的交叉效率值非常接近，仅存在微小不同。

表7 为本文交叉效率和经典交叉效率的排名，其中，第二列至第四列为本文交叉效率排名，第五列至第七列为经典交叉效率排名。由表7 发现，分别以理想前沿和非理想前沿为评价标准时，仅DMU9、DMU10和DMU14的排名差距较大，其他DMU 排名差距不大。而观察基于二者与基于理想前沿的模型可知，各DMU 的排名较为接近，与基于非理想前沿模型对比时大部分DMU 的排名均不同，且相差较大。

表7 本文交叉排序和激进型、仁慈型、中性交叉排序Tab.7 Orders of cross-efficiency in this paper and aggressive，benevolent and neutral cross-efficiencies

图2 为表7 第二至七列所获。由图2 可见，三类模型与激进型和仁慈型的交叉效率排名比较接近，但DMU8和DMU14与基于非理想前沿的排名存在明显差异。三类模型与中性交叉效率排序相比，DMU2的排名相同，其余决策单元与基于理想前沿和基于二者的排名存在差异，但差异较小，与基于非理想前沿相比时，大部分DMU 与其存在差异，在DMU5和 DMU11上差异明显。

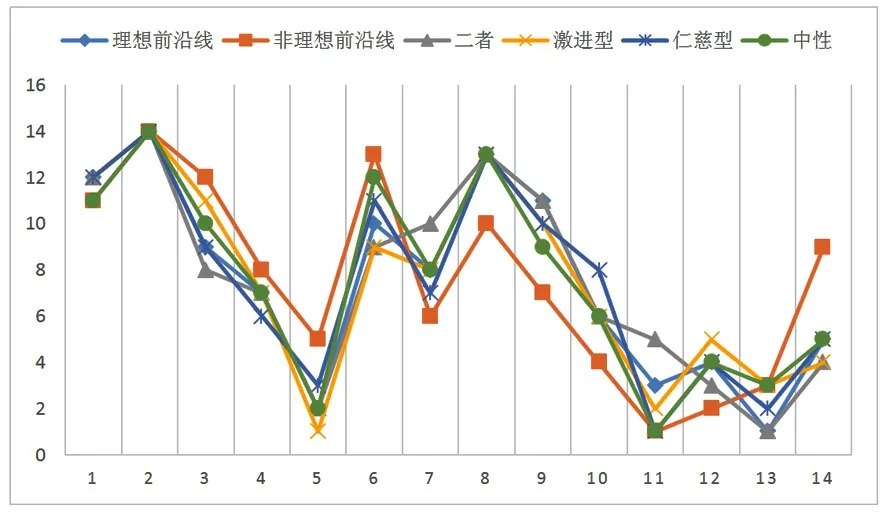
图2 本文交叉效率模型排序和激进型、仁慈型、中性交叉效率排序Fig.2 Orders of cross-efficiency in this paper and aggressive, benevolent, neutral cross-efficiency

4 结论

交叉效率评价方法是比较和排序决策单元的一种有效手段，本文以理想前沿线与非理想前沿线为评价标准，通过最小化DMU 与理想前沿线的最大偏差，或最大化DMU 与非理想前沿线的最小偏差，或结合二者建立相应模型确定一组最优投入产出权重，可对所有DMU 进行评价和排序。本文方法提高了传统DEA 模型的辨析能力。

从算例结果可见，与经典交叉模型相较，本文所提三类模型得出的效率值都在激进型和仁慈型效率值之间，缩小了交叉效率评价区间的长度，有效提高了效率评价的精度；基于理想前沿线与基于二者模型得出的效率值与经典交叉效率值比较接近，基于非理想前沿线模型得出的效率值与经典交叉效率值存在明显差距。因此，本文方法可以反映DMU 之间的绩效和特点，是一种有效、实用的交叉效率评价方法，能提供有价值的决策参考。