基于改进GRU 的城市供水管网流量预测研究
2023-05-25梁祥莹
夏 巍,汪 石,梁祥莹
(安徽建筑大学 电子与信息工程学院,安徽 合肥 230601)
城市供水管网的复杂程度随现代化城市的人口高密度增长而增长。为确保居民的用水稳定性,研究人员对供水管网的优化调度开展了深入探索[1]。供水管网的流量预测可以作为管网优化调度的依据。现阶段,城市供水管网的流量预测方法一般采用机器学习的算法[2-4],相对于传统回归分析方法,例如灰色模型[5]、自回归滑动[6],其预测精度更高、适用范围也更广。
城市供水管网流量数据作为典型的时序数列,具有良好的循环变动特性。许多领域采用循环 神 经 网 络[7](Recurrent Neural Network,RNN)分析时序数列,都获得了优秀的成果[8-9]。目前,基于循环神经网络的城市供水管网的流量预测研究不多,而基于长短期记忆网络(Long-Short Term Memory,LSTM)的日用水流量预测[10]已经在单个节点流量预测中得到了较好的结果。循环门单元(Gated Recurrent Unit,GRU)[11]算 法 作 为LSTM的变种,在样本数据较小的情况下具有更快的收敛速度以及较为优秀的预测精度。基于此,本文选择GRU 算法,针对某市供水管网优化调度系统的研究特点,预测监测节点的用水量。
现阶段对供水管网节点用水量的预测研究,多对单个节点的24 h 或者更长的历史数据来进行分析拟合,以推断下一天该节点的用水量[12-13]。这种方法对于单个节点的分析固然准确,但模型的泛化能力较差性,缺乏普适性。
因此,本文从多个监测节点的流量数据入手,以类似局部加权线性回归的思路优化GRU 网络,进行基于多节点的流量预测研究,并利用某市供水管网监测平台2020 年9 月1 日至7 日的4 个监测节点流量数据进行验证,对比优化前后的结果。
1 基于GRU 的流量预测模型
循环门单元(GRU)算法是LSTM 算法的一种变体,由于简化了控制门的结构,使得其在数据量相对较小的情况下,具有更快的模型收敛速度。
如图1 所示,不同于LSTM,GRU 模型只有重置门rt与更新门zt,其激活函数为Sigmod。前者用于控制来自前一状态的ht-1,将其保留到ht上;后者用于将来自前一状态的ht-1部分信息量载入当前状态。具体的计算方式如下:

图1 t-1 状态下的GRU 网络示意图Fig.1 Diagram of GRU network in t-1 state
式中,Wr,Wz,Wh为输入至隐含层神经元的权值,Wo为输出层的权值,yt为当前状态下输出层的真实输出,ht为当前状态下传递至下一状态的输出,即RNN 中的隐藏状态。
本文采用单层的GRU 网络模型进行流量预测,其架构如图2 所示。

图2 单层GRU 网络模型结构Fig.2 Single-layer GRU network structure
2 基于特化的局部加权法改进GRU流量预测模型
分析公式(1)~(3)发现,对于当前的输入[ht-1,Xt],GRU 网络中的权值Wr,Wz,Wh的更新规则以预测网络的损失函数为基础,平等对待24 小时的流量数据,忽略了实际生产生活中的用水规律。针对这一问题,本文以用水流量的相似性为基础,特化局部加权法,以优化GRU。
显然,流量数据ft、ft+24对应着昨天与今天同一时刻的用水流量,在实际生活中两个时刻的相似性较高;同样地,流量数据ft与前后一小时ft-1、ft+1的用水流量也具有很高的相似性。但受制于设备的采集间隔,连续性的流量数据被分割为间隔一小时的离散数据,极大降低了数据间的相似性,而采集间隔越短,这种相似性越高。那么,对应(ti,fti)可应用类似于局部加权线性回归[14-15]中的权值函数计算方法。这种方法的核心思想为,越靠近中心点ti的点,获得的权值越大,对于预测的结果影响更大;反之,离中心点越远的点则权值越小、影响力越小。

为了提高模型的泛化能力,将三个监测节点的流量数据作为训练样本,依次载入模型进行训练,并将另外一个监测节点的数据作为测试样本,用于验证模型。GRU 算法作为LSTM 算法的变种,其模型的输入方式有着类似的模式,包括单维单步、单维多步、多维单步以及多维多步。由于多监测节点模型的目的是提高其泛化能力,使网络能够适用于管网内的任一监测节点,此处采用单维多步的模式训练模型。训练样本的输入格式为inputtrain=(f1,…,fi),i=504。建立模型的目的是预测单日节点的用水量,因此依据采样周期,设置Timesteps=24,即用前24 小时的节点流量数据预测下一小时的流量。
3 实验结果与分析
本次研究采用python 编程语言,在Tensorflow、Keras 框架下构建GRU 网络模型。将Batchsize 设置为1,隐含层的神经元数量设置为30,网络的优化器选择adam 函数。所使用的数据皆取自某市供水管网监测平台采集的历史数据,包含城区工作区4 个监测节点的一周流量数据,数据采集周期为1小时。
将3 个监测节点一周的数据作为训练样本,另一监测节点数据作为测试样本。以当前日流量数据为输入;对应的后一天流量数据为输出。最终,在本实验中的输入即为W×inputtrain;W×inputtest。
实验结果如图3 所示。

图3 两种方法的流量预测结果Fig.3 Flow forecasting results of two methods
同时给出两种模型的均方根误差(RMSE)、平均绝对误差(MAE)与平均相对误差(MAPE),见表1。

表1 两种预测模型的均方根误差(RMSE)、平均绝对误差(MAE)与平均相对误差(MAPE)Tab.1 Root mean square error,mean absolute error and mean relative error of two prediction models
RMSE、MAE 与MAPE 都表明,改进后的GRU预测模型比改进前的预测效果更好、更可靠。分析图3 可以看出,在多数时刻,两种方法预测结果都实际值相近。但在用水量转折的时候,改进后的GRU 网络的预测值在大多数情况下都比改进之前更贴近实际值。这是由于改进的GRU 网络一定程度上放大了临近时刻数据值的影响。不过,依旧存在部分转折点的预测精度不够良好,如第42、第72时刻。
预测结果的差异性以误差频次分布表示,给出两种方法的预测误差频次分布图如下:
观察图4 可以发现,改进后的GRU 网络,在80%的时刻内,预测误差都在-10% ~ 10%范围内,60%以上的误差为-5% ~ 5%。而改进前的GRU网络的预测结果,结合图3 分析知,在用水流量出现转折时,预测误差较大,如在第25、42、72 时刻,甚至出现-40%、-60%的巨大误差,而改进后的GRU 将此误差缩小了15%以上。也正是这些转折处的较大预测误差,导致了改进前模型的误差在-10%~10%以内的频次不及改进后的模型,表明改进后的模型对多节点训练的流量预测准确性更高。
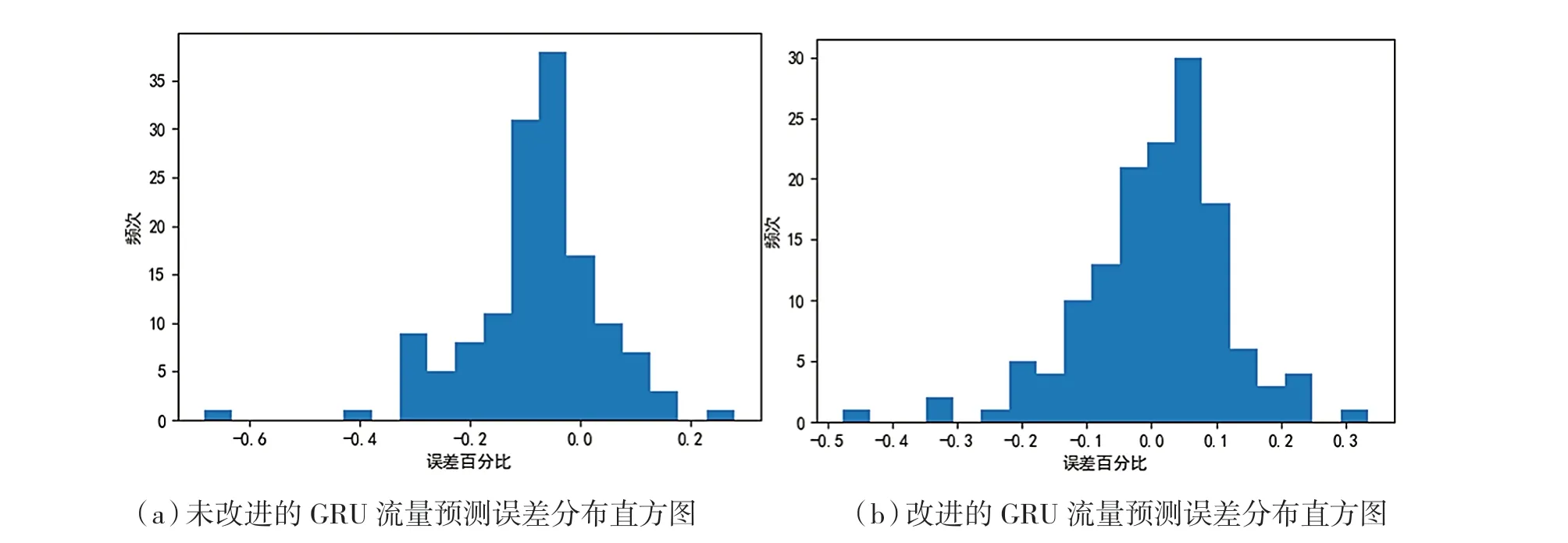
图4 误差分布直方图Fig.4 Error distribution histogram
4 总结
以流量相似性特化的局部加权回归的权值函数优化GRU 网络,在一定程度上提高了供水流量的预测准确性。同时,由于采用多个节点的数据进行学习和验证,虽然增加了训练时间,但较好地提高了模型的泛化能力,因而对管网流量预测具有更强的现实意义。
由于本文涉及项目的供水管网监测系统数据采集节点的采集周期较长(1 小时),获取两个相邻时刻的流量数据变化量较大,对预测的实时性和误差存在一定的影响。但是这个问题可以通过调整数据采集节点的采集周期改善,进一步提高本文所提模型的预测准确性和精度。
