以疑促思：引导学生追随学习需求自主探索——以“用数对确定位置”为例

江苏省南京市月华路小学 杨 玲

心理学认为，学习需求是指人对未知事物的渴求，为满足自身生产、生活以及发展的需求，并在学习动机驱使下的一系列反应。 “为学患无疑，疑则有进，小疑则小进，大疑则大进。”疑的背后隐藏着问题，教师要善于抓住学生的这种对新知的渴求，不断设计问题，诱发和激起学生的学习欲望，促使学生不断思考，积极主动地寻求解决问题的方法，促进其创新思维的发展。

一、设情生疑，引发思考

数学活动的核心是数学思考。多年的教学实践证明，学生的思维常常活跃于疑问的交叉点上。“疑”能让学生在心理上感到困惑，产生认知冲突，从而拨动他们的思维之弦，进而积极参与数学探究活动，对发现的问题进行验证释疑，自主解决问题。合理的情境选择能让学生产生疑问，促进思考。

片段一：

师：同学们，我们想要快速而准确地打到地鼠，需要知道地鼠的什么呀？

生：位置。

师：我们今天要玩一个“听指挥打地鼠”的游戏，我先请一位同学来打地鼠，这位同学要面对大家，其他同学观察石头前面地鼠出来的位置，然后大声而快速地告诉他地鼠在第几个洞，听明白了吗？准备好了吗？

生1：第4个。

生2：第3个。

师：我听到有人报4也有人报3，怎么回事？

生3：报4是从左往右数，报3是从右往左数。

师：那我们这位打地鼠的同学该听谁的呢？有什么办法能解决这个问题呢？

生4：全班统一。

师：你们准备怎么统一？

生5：从左往右数。

教师抛出疑问：“有人报4，有人报3，打地鼠的同学该听谁的？”学生思考后发现：虽然描述的是同一个洞，但由于大家的说法不同导致打地鼠的同学不知道该怎么办。为了解决这样的问题，学生自然会思考解决的方法。这样的问题“逼迫”学生去思考，大家在交流中明确：观察的角度不同，结果自然不同。教师继续追问：“有什么办法能解决这个问题呢？”学生自然而然就产生“需要统一数的方向”这样的想法。通过统一观察的方向——从左往右数，学生很好地解决了教师的疑问，为之后的学习做好铺垫。教师选择轻松有趣的小游戏导入，学生看似只是玩一玩，但在玩的过程中，参与游戏的学生发生了意见不统一的情况。面对这种境况，想要继续玩下去，学生只能想办法去解决，并在解决的过程中自然而然地学到知识。教师创设的情境既要能激发学生的学习兴趣，又要能和新知联系起来。合理的情境不仅能帮助学生释疑，而且能使学生在释疑的过程中主动而深入地思考，形成数学思想方法。

二、探究质疑，积累活动经验

教师要引导学生在数学活动中多积累经验，同时，教师要积极地利用学生的已有经验，发掘经验的价值，再度设疑，引发新的思考，提高学生主动思考、探究的能力。有了前面的学习经验，学生明白了想快速而准确地打到地鼠，必须统一意见，此时，教师要学会利用已有经验直接提问，促使学生去探究同类问题。

片段二：

1.打前思考。

师：这个游戏升级了，现在我们要告诉他地鼠的位置。要告诉他哪些数学信息？还能仅仅只用从左往右数这一句话来说吗？该怎么说才能正确表达出小地鼠的位置？

生1：是不是要规定从前往后数？

生2：可不可以从后往前数？

师：有人说从前往后数，有人说从后往前数，那我们统一一下，就从前往后数。我们来数数看。

2.第一次击打。

师：看清楚了吗？

3.第二次击打。

师：我们在游戏之前先商量好了怎样去数，且大家达成了一致。这么难的游戏我们都可以合作完成，真了不起！

有了第一次关于“统一”的活动经验，随着游戏的升级，教师直接提出问题：“现在我们要告诉他地鼠的位置，需要提供哪些数学信息？”有了第一次击打的经验，第二次击打前学生就会主动去思考该怎么更好地描述地鼠的位置。在第二次游戏时，教师并不是重复第一次的问题，而是设计了“打前思考”这样的环节，这次的思考跟第一次看到整个活动过程后的思考不一样，教师直接抛出问题，引发学生根据第一次的活动经验去思考，让学生在思考方式上积累经验。

片段三：

1.师：小地鼠钻来钻去，老师把它的3次探头都拍摄了下来，你们能很快地判断出它的位置吗？

2.第1次播放。

师：小地鼠探头了，又探头了……

（学生来不及判断）

师：你遇到了什么困难？

3.第2次播放。

师：第一只地鼠的位置你记录下来了吗？

生：第1行，第3列。

师：后面的来不及怎么办？你有什么好办法？

生：简写。

师：怎么记录？

生：老师，他记的是1,3 ，我记的是3,1.

师：不是同一只地鼠吗？怎么会有两个不同的位置？

生：列和行的顺序不一样。

师：有两种不同说法肯定是不行的，怎么办？

生：那我们也要来规定，我们可以用第1个数字表示列，第2个数字表示行。

4.提炼数对。

师：在数字两边加上括号，中间用逗号将数字隔开，就是数学上说的数对，今天我们学习的就是“用数对确定位置”，数对怎么读呢？读作数对三一，也可以直接读三一，我们一起来读一读。

教师通过层层升级的问题，促使学生主动去思考如何解决问题。学生通过主动交流后积极改正，进一步形成自己的解决方法。教师先抛出疑问“怎么办”，学生接收后主动形成自我反问，最后在评价中逐步完善表示方法。这一过程，也体现了“以生为主”的理念，促进学生在独立思考、自主探究、互动交流中解难释疑，积累活动经验。

三、提炼释疑，感受规定的合理性

苏霍姆林斯基认为，每个儿童的内心深处都希望自己是一个发现者、探索者与研究者，教师要教会学生怎样去思考，让学生独立、主动地去探索知识，将知识的学习过程不断内化，才能满足学生的学习需求。教师应当根据学生的“最近发展区”提出合理的问题，在激发学生兴趣的同时使学生产生强烈的求知欲和探究欲。

片段四：

1.回忆学习过程，提炼学习方法。

师：同学们，咱们来回忆一下，一开始我们打一排地鼠，为了让打地鼠的同学能快速且准确地打到地鼠，我们做了什么事情？

生：统一了从左往右数。

师：是的，后来有很多排地鼠，我们又做了什么事？

生：统一了从前往后数。

师：为了准确记录位置，我们又统一了先写列后写行。一共进行了三次统一。

2.从生活中的实例发现统一的合理性。

师：同学们，我们的教室中也有数对。来跟着老师一起数一数。这边是第1列，请一位同学站起来给大家看一下。

师：哪边是第一行呢？

师：同学们，如果把你们的位置搬到屏幕上，你们能找到自己的位置吗？

3.国际象棋中的数对。

师：数学来源于生活，又服务于生活。我们来看国际象棋中的数对知识（见图1）。

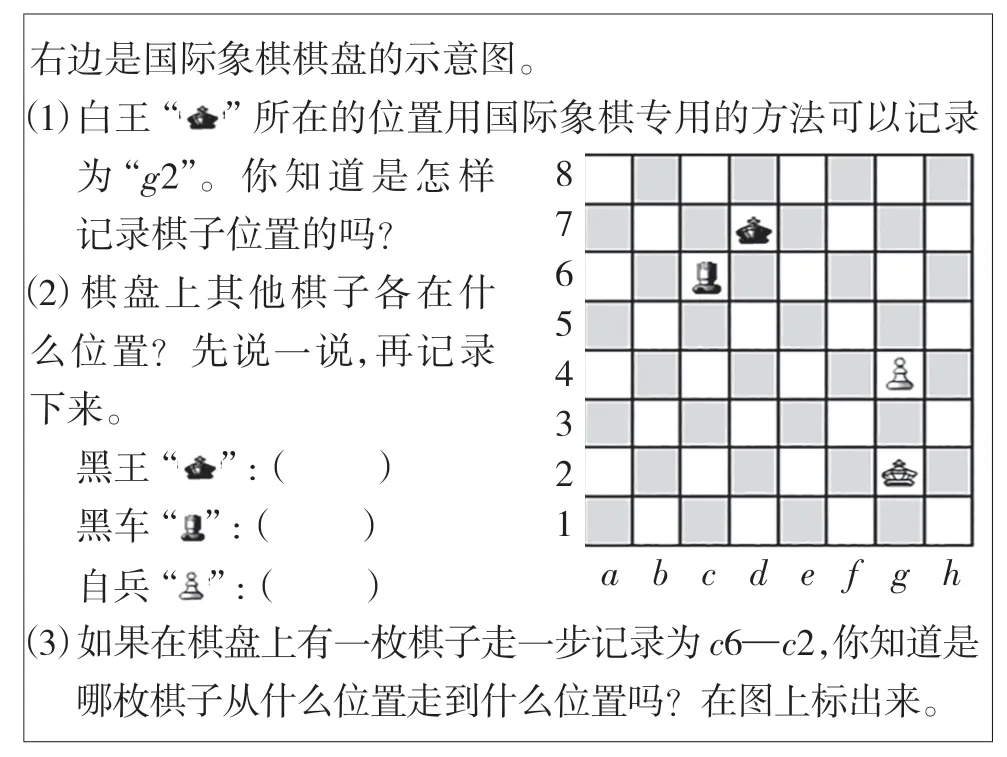
图1

师：想一想，国际象棋的规定和我们今天学习的数对有什么关系？

教师在帮助学生回忆知识的过程中提问：“我们做了什么事情？” “我们又做了什么事？”不断让学生在回忆的过程中提炼方法，感受规定的合理性。教师设计了将班级座位搬到屏幕上的这一环节，并要求学生将其进行对应，如此，轻松地解决了教室座位的平面图和学生实际座位之间的关系，很好地突破了难点，并让学生感受到数学来源于生活。学生经过了本节课的学习，会产生豁然开朗的感受。教师紧抓学生的心理需求，引导学生主动参与知识的形成过程，将问题生活化的同时，由浅入深地引导学生逐渐形成问题链而持续地思考与分析，这样不仅拓宽了学生的求知思路，还让学生的思维在释疑中得以有效发展，同时，学生也能感受到数学规定来源于生活以及规定的合理性。

总之，数学教学是学生获取知识、发现真理、答疑解惑的过程，教师应创造合理的问题情境，让学生在真实可感的情感体验中形成积极思考的习惯；应设计有效的问题串，让学生在探索的过程中形成持续思考的习惯；应通过提问来帮助学生回忆整个学习过程，让学生在总结的过程中形成深入思考的习惯。教师要在课堂学习的过程中让学生经历设疑、质疑、释疑的思考过程，在以疑促思中构建高效的数学课堂，为学生学习能力的可持续发展奠定坚实的基础。