基于改进PSO 算法对榴弹最佳杀伤面积的计算

刘双庆，杨 臻，郁卫星，王永艳

（中北大学机电工程学院，太原 030051）

0 引言

榴弹是战场上最常见的武器，榴弹在空中爆炸时，爆炸产生的冲击波在空气中迅速减弱，对于远距离目标的打击作用，主要是靠破片的杀伤效应，榴弹毁伤威力的评判标准是杀伤面积，其中影响杀伤面积的因素有落速、落角和炸高［1-3］。马永忠等通过编程计算的方式对影响杀伤面积的主要因素进行了分析［4］。孙韬等通过数值模拟和试验的方法得到了有效炸高的范围，其炸高的上下限值相差达到1.7 m［5］。应国淼等基于射击线技术对杀伤面积进行了计算［6］。上述文章均需要采用传统的计算方法要根据所需要结果的精度，通过数论网格法来计算，由于计算点数的限制，导致计算结果不够精确。赵新通过欧拉距离法改进了粒子群算法，通过引战配合的方式，以对地面立姿人员为毁伤目标，确定了不同落角情况下榴弹最佳炸高值，相比于传统算法，计算结果精度更高［7］。在实际作战中，卧姿人员更符合实际情况，但该文章未对卧姿人员和榴弹落速对杀伤面积的影响进行分析计算。

本文从杀伤面积与落速、落角和炸高的关系入手，以卧姿人员为毁伤目标，建立杀伤面积数学模型，利用PSO 算法来解决最优化的问题，应用随机惯性法对标准PSO 算法中的惯性权重进行调整，解决PSO 算法前中期局部搜索能力和后期全局搜索能力不足的问题，此方法既能减少粒子数量，又能提高收敛速度，对比传统计算方法，计算结果精度更高。

1 数学模型建立

1.1 杀伤面积数学模型

杀伤榴弹质心在地面上的投影为坐标原点O，令xoy 为地面，z 轴垂直于地面，建立坐标系如图1所示：M 为目标点；h 为炸高；θc为落角；α 为弹体和目标的连线与地夹角；φ 为破片飞向角；R 为弹体与目标的距离。

图1 杀伤榴弹空炸坐标图Fig.1 Coordinate graph of air burst of fragmentation grenades

杀伤榴弹在设计时，其威力已经固定，所以杀伤榴弹在攻击地面敌方战斗人员时，杀伤面积会受到炸高、落角和落速的影响，杀伤面积可以表达为杀伤概率在目标平面上的积分［8］，其表达式为：

式中，S 为杀伤面积；h 为炸高；θc为落角；vc为落速；p 为杀伤概率，其表达式为：

式中，Sv为目标暴露面积；Ω（x，y）为杀伤破片的球面分布密度，其表达式为：

式中，N0为有效破片数目；φ 为破片飞向角；ρ（φ）的表达式为：

式中，f（φ）为密度分布函数。

1.2 破片空间分布规律

战斗部静止爆炸时，破片静态飞向角为φ1，破片速度为v1，可以近似将破片分布密度看作是呈平缓的正态分布，静态密度分布函数为：

式中，Nφ1为在φ1旋成的圆锥角内的破片数目；dNφ1为φ1变化dφ1时破片数目的变化量；σφ1为飞向角的均方差；φˉ1为飞向角的期望，其值通常取π/2。

战斗部在动态爆炸时，还存在弹体落速vc，如图2 所示。vd为叠加后的破片速度，φ2为破片动态飞向角。动态爆炸时的杀伤破片的球面分布密度表达式为：

图2 破片飞向示意图Fig.2 Schematic diagram of the direction of flying fragments

由图2 几何关系得：

1.3 卧姿人员受弹面积

在研究杀伤面积时，一般采用长方体作为人体等效目标，长方体的尺寸为1.5 m×0.5 m×0.25 m，人员的受弹面积与其位置，姿态，战斗部位置都有关。在战场环境中，人员姿态多为卧姿，故以卧姿人员为主要研究目标。在计算目标人员受弹面积时，以人员外表面在垂直炸弹目标连线的投影为主；总体受弹面积分为两部分，一部分为顶部受弹面积Sv1，另一部分为侧面受弹面积Sv2，如下页图3 所示。

图3 人员单位受弹部位示意图Fig.3 Schematic diagram of the parts under fire for personnel

顶部受弹面积Sv1的表达式为：

侧面受弹面积Sv2：

假设各个人员姿势目标相位角β 出现几率相等，则侧面积在垂直地平面的投影面积Sl为：

将式（2）、式（7）和式（11）表达式代入式（1）中，即可得到杀伤面积表达式。

2 PSO 算法

PSO 算法是一种智能优化算法，其全称为粒子群优化算法，在上世纪90 年代中期，美国学者Kennedy 和Eberhart 源于对鸟类群体觅食行为提出了此算法，核心思想是利用群体中个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解，可用于多变量优化问题中［9-10］。

2.1 PSO 算法流程

在n 维搜索空间中，粒子i 的当前位置Xi=（Xi1，Xi2，…，Xin），当前飞行速度Vi=（Vi1，Vi2，…，Vin），最佳位置pbesti=（pbesti1，pbesti2，…，pbestin）。

对于求解最大值问题，令g（X）目标函数，确定粒子i 最好位置的表达式为：

式中，d 为迭代次数。

种群中粒子数为M，种群中所有粒子所经历过最好的位置为gbest（d），即：

式中，ω 为速度惯性权重；c1为粒子的个体学习因子；c2为粒子的社会学习因子；r1、r2为［0，1］两个相互独立的随机数；Vid为第d 次迭代时，第i 个粒子的速度；Xid为第d 次迭代时，第i 个粒子的位置；pbestid为第d 次迭代为止，第i 个粒子所经过最好的位置；gbestd为第d 次迭代为止，所有粒子所经过最好的位置。

算法流程如图4 所示。

图4 PSO 算法流程图Fig.4 PSO algorithm flow chart

2.2 改进PSO 算法

PSO 算法中，惯性权重体现的是粒子继承先前速度的能力，SHI Y 最先将惯性权重引入到PSO 算法中，并分析指出一个较大的惯性权重值有利于全局搜索，而一个较小的惯性权重则更有利于局部搜索，因此，提出了线性递减惯性权重。标准PSO 算法中，使用最多的就是线性递减惯性权重，表达式如下［11-12］：

式中，ωmax为开始迭代式时惯性权重；ωmin为迭代结束时惯性权重；K 为迭代总次数。

前期ω 的值较大，缺乏局部搜索能力，但随着迭代次数的增加，惯性权重ω 的值越来越小，缺乏全局搜索能力，计算过程中可能造成过早收敛于局部最优值，而不是收敛于全局的最优值。本文利用随机惯性权重法对PSO 算法中的惯性权重进行改进，可以有效避免在迭代前期局部搜索能力的不足，也可以避免在迭代后期全局搜索能力的不足，随机惯性权重的表达式为：

式中：rand 为［0，1］均匀分布随机数；randn 为正态分布的随机数；σ（标准差）用来度量随机变量权重ω 与数学期望之间的偏离程度，主要目的是来控制权重误差，使权重有利于向期望权重方向进化。

通过引入随机惯性权重的方法，提高种群的搜索能力，可以减少粒子数量来提高计算速度，并且精度和收敛速度都可以提高，改进前后惯性权重如图5 所示。

图5 惯性权重对比图Fig.5 Inertia weighting comparison chart

2.3 实例计算

根据以上理论分析，所要优化的数学模型表达式为：

模型相关的初始值为：N0=3 527；v1=1 000 m/s；σφ1为飞向角的均方差，取π/6.7；ωmax=0.9；ωmin=0.4；K=100；σ=0.3；c1=c2=2。

3 计算结果与分析

3.1 计算结果与分析

当榴弹落速为200 m/s 时，炸高、落角和卧姿人员杀伤面积的关系如图6 所示。当落角为10°、30°、50°、70°、90°时，炸高和卧姿人员杀伤面积的关系如图7 所示。当炸高为1 m，5 m，10 m，15 m，20 m 时，落角与卧姿人员杀伤面积的关系如图8 所示。

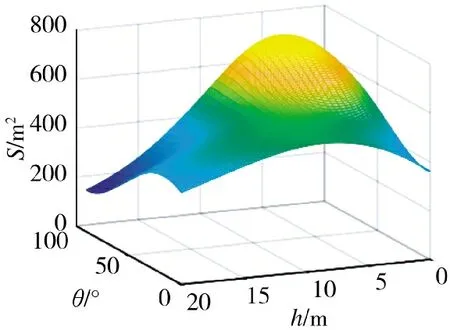
图6 落速200 m/s，炸高、落角和卧姿人员杀伤面积关系图Fig.6 Killing area relationship chart of，burst height，angle of falling and personnel in prone position with the falling speed of 200 m/s

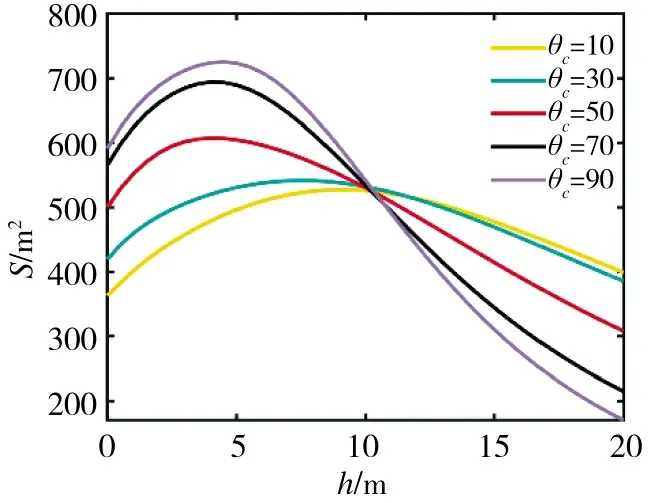
图7 落速200 m/s，炸高与卧姿人员杀伤面积曲线图Fig.7 Killing area curve graph of，explosive height and personnel in prone position with the falling speed of 200 m/s

图8 落速200 m/s，落角与卧姿人员杀伤面积曲线图Fig.8 Killing area curve graph of falling angle and personnel in prone position with the falling speed of 200 m/s

当榴弹落角为90°时，炸高、落速和杀伤面积的关系图，如下页图9 所示。当落速为100 m/s、150 m/s、200 m/s 时，炸高和杀伤面积的关系如图10 所示。

图9 落角90°时，炸高、落速和杀伤面积关系图Fig.9 The relationship diagrap among burst height，fall speeding and killing area with the falling angle of 90°

图10 落角90°时，炸高与杀伤面积曲线图Fig.10 The curve diagrap of burst height and killing area with the falling angle of 90°

当落速为200 m/s，用传统方法、PSO 算法和改进PSO 算法对落角15°、30°、50°、70°、90°求解最大杀伤面积和达到最大杀伤面积时所对应的炸高，如表1 所示。

表1 落速200 m/s 时，杀伤面积、炸高、落角对应的结果Table 1 The results corresponding to killing area，burst height and angle of falling at a falling speed of 200 m/s

当落角为90°时，用传统方法和改进PSO 算法对落速100 m/s、150 m/s、200 m/s 求解最大杀伤面积和达到最大杀伤面积时所对应的炸高，如表2所示。

表2 落角90°时，杀伤面积、炸高、落速对应的结果Table 2 The results corresponding to killing area，burst height and falling speed with the falling angle of 90°

3.2 结果分析

由图6 和图7 中可看出，随着炸高的增加，杀伤面积先增大后减小，其主要原因是，炸高较低时，破片较为集中，作用到目标区域上的破片数量较少，杀伤面积较小；当炸高较大时，作用到目标区域的破片数量减少，所以杀伤面积较小；当炸高超过某一数值时，随着落角的增大，杀伤面积衰减得越快，主要原因是，大落角时，榴弹所产生的破片几乎平行于地面飞行，大部分破片飞向空中，作用到目标区域内破片数量减少。

由图8 可以看出，当炸高为1 m 时，其杀伤面积要比5 m 时小得多，主要原因是飞到目标区域的破片较为集中，导致杀伤面积较小。当炸高为1 m 和5 m时，随着落角的增大，杀伤面积逐渐增大；当炸高大于5 m 时，落角存在最优值，使得杀伤面积最大。

从图9 和图10 可以看出，随着落速的增加，对杀伤面积的影响并不大，主要原因是，破片的速度要比落速大得多，对破片的飞行轨迹造成的影响较小。

从表1 和表2 可以看出，改进PSO 算法对比传统方法，改进PSO 算法对最大杀伤面积和炸高的计算精度明显高于传统方法，其最大的炸高误差超过0.1 m。改进PSO 优化算法对比标准PSO 算法在落角为30°的计算时，改进的PSO 算法精度要更高。

图11 为PSO 算法的优化过程，标准PSO 算法粒子数为10，改进PSO 算法粒子数为5，改进PSO算法所需的粒子数量更少，且收敛速度更快。

图11改进PSO 算优化过程Fig.11 Optimization process of improving PSO calculation

4 结论

本文提出了计算榴弹最佳杀伤参数的高效计算方法。首先，以卧姿人员为研究目标，建立了榴弹杀伤面积的数学模型。其次，基于随机惯性权重法对PSO 算法进行了改进，并以最大杀伤面积为目标函数，计算得到本文条件的榴弹，其最优落速、落角和炸高的组合为200 m/s，90°，4.457 9 m。对比标准PSO 算法，改进后的算法所需的粒子数量更少，收敛速度更快，从而计算效率更高。本文计算方法可为榴弹最佳杀伤参数的设计提供依据，同时也为毁伤效能评估提供了一种高效的计算方法。