能量收集分布式基站系统的下行射频远端选择

黄志民,肖 琨

(广西师范大学 电子工程学院,广西壮族自治区 桂林 541000)

1 引 言

从可再生能源,如太阳能、风能、热能和射频(Radio Frequency,RF)能中获得能量的能量收集(Energy Harvesting,EH)技术可以驱动通信设备和网络[1-3]。能量收集技术已被应用于一些低功耗系统中,如D2D(Device to Device)通信、CR(Cognitive Radio)传感器网络以及分布式天线系统(Distributed Antenna System,DAS)等方面[4-8]。文献[9]中通过联合优化无人机飞行轨迹、用户传输功率和任务完成时间,实现了基于能量收集的无人机无线通信系统的总能耗最小化。文献[10]结合智能电网来实现能量收集技术、能量共享和动态定价的联合优化,以帮助降低系统能耗。

在分布式基站系统中,射频远端根据需求分布在小区的各个位置,使用户与分布式基站系统天线之间的距离更短,具有高覆盖率、抗衰落能力强等优点[11]。文献[12]在分布式天线系统中通过对RAU(Remote Antenna Unit)的功率分配方案,提出了最小数据速率约束下的信息速率最大化问题。文献[13]在分布式系统中将RRH(Remote Radio Heads)分为能量收集区与干扰区,能量收集区的RRH为能量受限用户供电,并基于两种不同的信道状态信息评估系统的频谱效率,得到了新的EH-DAS系统遍历频谱效率的精确表达式和界表达式。文献[14]讨论了使用PS(Power Splitting)模式的SWIPT(Simultaneous Wireless Information and Power Transfer)能效最大化问题,提出了频谱与能效折中的分布式端口功率分配方案,改善了传统迭代算法的性能,降低了算法的复杂度,在节省能源的情况下最大限度地提高了误码率。文献[15]在能量收集技术与电网的结合下,考虑RAU功率约束和各种智能电网因素,基于能量合作的功率分配策略,最大化信息速率和能量传输速率,证明了最优功率策略具有双阈值结构。文献[16]中提出了一种分布式天线系统下的能量共享模型,通过在基带侧增加共享装置以及对电网提供统一接口,能够在能量短缺或过剩时向电网购买或出售能源,构建出不同的能量管理模式。文献[17]中针对波束形成联合天线选择的分布式天线系统,提出了能效最大化的问题,并基于梯度投影法导出有效的功率分配闭式,最大化能效的最优和次优功率分配方案。文献[18]中基于新的欧氏距离选择算法在分布式天线系统中选取最优RAU集合,并提出三层迭代算法优化传输预编码矩阵,实现能量效率的最优化。文献[19]中通过选择RAU在每个时隙进行通信,提出动态优化RAUs的双工模式,针对非凸双工模式的优化问题,推导出一种基于并行逐次凸逼近的非凸双工模式优化算法。文献[20]中通过波束赋形和关闭不必要的RAU来最小化总的消耗,利用凸规划的差异性和混合范数进行逼近求解,所提算法显著地降低了传输功耗。

可见,关于分布式基站系统的端口和天线选择问题已经有不少的研究成果。但是,这些研究都基于传统的分布式基站系统。对于能量收集分布式基站系统而言,每个射频远端都可以进行能量收集,能量的存储设计对于系统的性能和部署关系重大。如果在射频远端配置能量存储单元,会增大射频远端的体积和重量,不利于系统部署。如果在基带处理侧配置能量存储单元,可以有效地解决这一问题。但是该情形下的射频远端选择与能量在系统中的调度密不可分,具体解决方法尚未见报道。基于此,笔者致力于在能量收集分布式基站系统中开展相关问题的研究,以解决能量集中存储在基带处理侧时的射频远端选择问题。文中首先建立能量集中存储在基带处理侧时的分布式基站系统模型;继而以最大化信息传输速率为目标,建立波速赋形、能量共享、功率分配联合优化的系统优化问题,并从收集能量部分共享和完全共享两个角度进行问题求解,在此基础上形成了所述模型的射频远端选择策略。

2 系统模型和问题描述

2.1 EH-DBS模型

图1所示的能量收集分布式基站系统(Energy Harvesting Distributed Base-station System,EH-DBS)模型中,EH-DBS由位于近端的基带处理子系统(Baseband Processing Sub-system,BPS)、位于远端的射频子系统(Radio Frequency Sub-system,RFS)和位于近端的能量子系统(Energy Harvesting Sub-system,EHS)构成。BPS集中承担分布式基站系统的基带处理功能,能够通过远程链路获取能量收集装置(Energy Harvesting Equipment,EHE)的能量,收集信息与射频远端侧的信道信息,并对系统进行资源调度。RFS包括N个射频远端(Remote Radio Frequency Unit,RRFU),每个RRFU配置M根天线。EHS由1个能量池(Energy Pool,EP)和N个与RRFU一体化的EHE组成。分布式基站系统的能量供应由EHS承担,具体来说,EHE负责能量的收集,EP负责能量的存储,能量的分配由BPS和EP配合完成。BPS执行在文中第3节所述的RRFU选择算法确定能量共享策略,通过优化问题求解功率分配,并向EP发出指令,输出实现功率分配所需的能量。出于降低设备体积和重量的考虑,RRFU不配置能量存储设备,可采用两种不同的方式利用所收集的能量。方式一为RRFU收集的能量首先给自身使用,过剩的能量输送到近端的EP,把这种方式称为部分共享方式;方式二是RRFU收集的能量首先全部输送到近端的EP,由BPS和EP对能量进行分配,再将分配的能量输送给RRFU,把这种方式称为完全共享方式。

图1 EH-DBS系统模型

设第i个RRFU的发射功率为pi( 1≤i≤N),则

pi=vE,i+vB,i-vS,i,

(1)

其中,0≤pi≤pmax,pmax为RRFU的功率限制。各RRFU的设备类型相同。第i个RRFU的能量收集速率为vE,i,显然vE,i>0;第i个RRFU由于能源短缺从EP借用能量的速率为vB,i,vB,i≥0;第i个RRFU由于能量过剩输送EP的速率为vS,i,vS,i≥0。

(2)

其中,ηE-E(0<ηE-E<1)为EP和EHE之间能量传输链路的能量传输效率,反映了能量在传输过程中的损耗情况。

用户设备(User Equipment,UE)接收的信号可表示为

(3)

其中,gi表示第i个RRFU与UE之间的M×1维信道系数向量,其各元素为零均值单位方差的高斯随机变量;wi为第i个RRFU的1×M维波束赋形向量,且‖wi‖2=1[17];x表示零均值单位方差的传输信号;n表示具有零均值和方差为σ2=1的加性高斯白噪声。于是用户设备获得的传输速率为

(4)

2.2 研究思路与问题描述

以最大化下行传输速率为目标,优化问题可以建模为

(5)

(5-1)

0≤pi≤pmax, ∀i∈{1,2,…,N} ,

(5-2)

vB,i≥0,vS,i≥0, ∀i∈{1,2,…,N} ,

(5-3)

‖wi‖2=1, ∀i∈{1,2,…,N} ,

(5-4)

其中,Ω表示N个RRFU的集合。约束条件式(5-1)反映了EP的能量存储能力限制,约束条件式(5-2)反映了RRFU的发射功率限制,约束条件式(5-3)为EP与EHE之间的能量交互情况,约束条件式(5-4)反映了波束赋形向量限制。

优化问题的求解有必要设计有效的波束赋形方案。考虑到‖wi‖2=1,由文献[21]可知实现最佳系统性能的波束赋形向量可定义为

(6)

于是,优化问题式(5)进一步表示为

(7)

(7-1)

0≤pi≤pmax, ∀i∈{1,2,…,N} ,

(7-2)

vB,i≥0,vS,i≥0, ∀i∈{1,2,…,N} 。

(7-3)

在求解优化问题式(7)的过程中,为获得最优的RRFU与EP的交互策略,参考文献[15]可知第i个RRFU与EP之间存在3种能量交互情况:(1)第i个RRFU只输送能量至EP,此时vB,i=0,vS,i>0;(2)第i个RRFU只从EP借用能量,此时vB,i>0,vS,i=0;(3)第i个RRFU与EP无能量交互,此时vB,i=0,vS,i=0。

3 优化问题求解

在求解优化问题(7)时,按照部分能量共享和完全能量共享两种情形分别求解,获得相应的能量策略。

3.1 部分共享时的优化问题求解

在部分共享的情形下,RRFU收集的能量先用于满足自身传输的消耗,再将过剩的能量输送至能量池。

由于问题式(7)是凸优化问题,利用卡罗需-库恩-塔克(Karush-Kuhn-Tucker,KKT)条件[22],可得拉格朗日函数:

(8)

其中,κi,λi,τi,θi,ξ,ω是相应的拉格朗日乘子。互补松弛约束为

κipi=0,λi(pmax-pi)=0 ,

(9)

τivB,i=0,θivS,i=0 ,

(10)

(11)

由于能量收集的随机性,有必要进一步明确EH-DBS使用能量部分共享策略的前提。假设集合Θ表示只输送能量至EP的RRFU的集合,集合Ψ表示只从EP借用能量的RRFU的集合,集合Φ表示与EP无能量交互的RRFU的集合,满足{Θ}+{Φ}+{Ψ}={Ω},进而推导部分共享策略下,所有RRFU使用最大功率传输的条件。

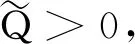
(12)

时,EH-DBS采用能量部分共享策略,且pi=pmax,∀i∈{1,2,…,N},是RRFU的最优功率分配方案。

(13)

即

由节2.2可知EP与RRFU之间在不同能量交互情况下的RRFU集合的资源调度为

(15)

(16)

(17)

将式(15)～(17)代入到式(14)中,有

(18)

再由式(15),可将式(18)写为

(19)

整理得

(20)

(21)

最后可得

(22)

(23)

(24)

从RRFU的功率约束可知,第k个RRFU的功率分配为以下3种情况:

(25)

由约束式(9),可知当pk=0时,κk>0,λk=0,ω≥0,则

(26)

在式(26)中,等号右侧除f(pk)外皆为有限常数,并且当pk→∞时,有f(pk)→∞,故 ∂L/∂vB,k→∞。同理可得∂L/∂vS,k→∞。以上不满足KKT条件,故pk=0非最优解。

当pk=pΔ时,κk=0,λk=0,ω≥0,有

(27)

在式(27)中,有f(pk)>0,τk≥0,ω/ηE-E≥0恒成立,故∂L/∂vB,k>0,不满足KKT条件,则pk=pΔ非最优解。

当pk=pmax时,κk=0,λk>0,ω≥0,有

(28)

(29)

(30)

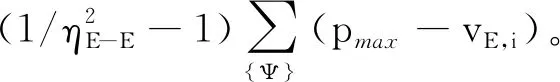
3.2 完全共享时的优化问题求解

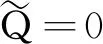
(31)

即各RRFU收集的能量将全部用于系统通信。利用注水算法,可得优化问题:

(32)

由柯西-施瓦兹不等式,可知

(33)

上式当且仅当(p1)1/2/‖g1‖=(p2)1/2/‖g2‖=…=(pN)1/2/‖gN‖时等号成立。通过该不等式,可将问题式(32)写为

(34)

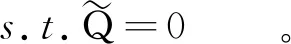
(34-1)

用拉格朗日数乘法求全局最优解,得

(35)

其中,ϑ为约束条件式(34-1)对应的拉格朗日乘子。

对式(35)求关于pi的偏导,得

(36)

解得

(37)

其中,(•)+表示取非负值。ϑ又可由限制条件式(31)得到:

(38)

(39)

其中,μ=1/(Nϑln2),为注水算法的水位线,∀i∈{1,2,…,N}。

综上,在对EH-DBS进行功率分配时,先判断条件式(12)是否成立。若成立,则采用能量部分共享方式;如不成立,则采用能量完全共享方式。

4 EH-DBS的RRFU选择算法

在RRFU选择过程中,RRFU实时收集各自的能量收集情况以及信道状态,并将信息传输给BPS。BPS依据所收集的信息确定系统的能量共享方式,并依据优化问题的解确定功率的分配方案以及选择最优的RRFU组合对用户设备通信,并指示EP向对应的RRFU传输指定的能量。

4.1 RRFU选择步骤

在求解优化问题(7)的基础上,设计从N个RRFU中选取L个RRFU参与对用户设备的下行链路传输的算法。具体步骤如下:

步骤① 设N个RRFU全部参与用户设备的下行链路传输,判断引理1中的式(12)是否成立。如果成立,转步骤②;否则,转步骤③。

步骤② 系统采取能量部分共享策略,N个RRFU的最优功率分配为满功率发射,转步骤④。

步骤③ 系统采取能量完全共享策略,N个RRFU的最优功率分配如式(38)所示。

4.2 复杂度分析

5 仿真结果与分析

利用所述EH-DBS模型对所提RRFU选择算法进行蒙特卡罗仿真,得出了仿真结果,并与贪婪算法、最大范数算法、随机算法、文献[18]中的选择算法以及与文献[20]中的无能量共享最优选择算法进行了对比分析。在仿真中, 用户设备与RRFU之间的小尺度衰落服从瑞利分布。具体仿真参数如表1所示。

表1 仿真参数

图2给出了所提算法和其他文献中算法的平均信道容量随选取的RRFU数量之间的关系。图3给出了不同RRFU选择算法的平均能量效率随选取的RRFU数量变化的曲线。

从图2中可以看出,随着选取的RRFU数量的增多,各算法的平均信道容量保持增长。其中笔者所提算法的性能最优,仅选取少数RRFU即可接近最大平均信道容量。选取10个RRFU时的平均信道容量达到了最大平均信道容量的98%,有助于减少系统功耗和节省资源开销。随机选择算法的性能最差,其余算法的性能居中。

图2 不同RRFU选择算法的系统信道容量

从图3中可以看出,随着选取的RRFU数量的递增,EH-DBS的平均能量效率逐步下降。这是由于系统信道容量的增速小于系统功耗增速所致。此外,从图中还可以看出所提算法的平均能量效率优于其他算法。

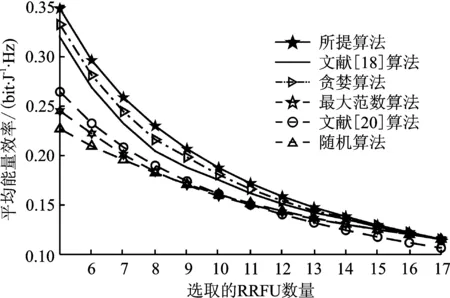
图3 不同RRFU选择算法的系统能量效率

图4给出了不同能量传输效率下平均信道容量随选取的RRFU数量变化的曲线。图5给出了不同能量传输效率下平均能量效率随选取的RRFU数量变化的曲线。

从图4中可知,在能量传输效率不变时,随着选取的RRFU数量的增加,系统的平均信道容量相应增长;对于不同的能量传输效率,系统的平均信道容量随着能量传输效率的增大而增大。

图4 不同传输效率的系统信道容量

从图5中可知,平均能量效率随着选取的RRFU数量的增加而逐渐减小,这是由于系统信道容量的增速小于系统功耗增速所致。对于不同的能量传输效率,系统的平均能量效率随着能量传输效率的增大而增大。

图5 不同传输效率的系统能量效率

图6给出了不同最大能量收集速率下平均信道容量随选取的RRFU数量变化的曲线。图7给出了不同最大能量收集速率下平均能量效率随选取的RRFU数量变化的曲线。

从图6中可知,在最大能量收集速率不变时,随着选取的RRFU数量的增加,系统的平均信道容量相应增长。对于不同的最大能量收集速率,较大的最大能量收集速率对应的系统平均信道容量大于较小的最大能量收集速率对应的系统平均信道容量,这是由于较大的最大能量收集速率意味着系统可以收集更多的能量用于通信,为采用能量部分共享的能量交互策略提供了条件,从而有效地减少了RRFU与EP之间传输能量时的能量损耗,能够更好地满足系统对能量的需求。

图6 不同能量收集上限的系统信道容量

从图7中可知,在最大能量收集速率不变时,随着选取的RRFU数量的增加,系统的平均能量效率逐步减小。对于不同的最大能量收集速率,较大的最大能量收集速率对应的系统平均能量效率大于较小的最大能量收集速率对应的系统平均能量效率,这是由于较大的最大能量收集速率意味着系统能够收集较多的能量,获得较大的系统信道容量,同时为采用能量部分共享的能量交互策略提供了条件,从而有效地减少了RRFU与EP之间传输能量时的能量损耗。

图7 不同能量收集上限的系统能量效率

6 总 结

笔者研究并仿真验证了能量收集分布式基站系统的射频远端选择性能,在建立系统模型的基础上形成优化问题并求解得到了最优的功率分配策略,形成了有效的射频远端选择算法。所建立的系统模型在射频远端不需要配置能量存储设备,降低了系统部署的难度,对于系统运营有积极的意义。能量子系统的配置有助于在各射频远端之间实现收集能量的共享,提高了系统的通信效率。同时,笔者提出的系统模型不需要提供电网、大容量电池之类的外部能源,仅依赖自身收集的能量维持系统运行。仿真结果表明,与现有的其他文献中的算法比较,笔者所提算法在平均信道容量、平均能量效率等方面具有良好的性能,为能量收集分布式基站的设计与应用提供了参考。