极化码在水下光通信系统中的应用研究

邢莉娟,李 卓,王庆港

(西安电子科技大学 综合业务网理论及关键技术国家重点实验室,陕西 西安 710071)

1 引 言

近年来,随着对海洋的勘测、开发和利用逐渐被重视,水下高效通信变得极其重要。而光学技术的使用解决了声通信或者电磁波等非光学通信系统中信号传输速率较低的问题[1],同时400 nm～550 nm波长范围内的蓝绿激光光谱已经被证实在海水中具有低衰减的特性,能够满足在水下进行大数据传输以及信号传输可靠性的要求,同时也为水下光通信系统的研究与发展奠定了坚实的理论基础。

由于水下粒子会使激光产生多重散射,从而使信号产生严重的多径效应和随机衰落,同时水质条件的不同也会对水下光通信的性能产生很大影响。近年来,随着信号处理等理论技术的不断提升和计算机性能的逐步增强,近香农限信道编译码、多载波调制技术等先进的信号处理技术得以引入到光通信领域,其中,信道编码技术是解决强干扰和强衰落性的关键技术之一。目前,水下光通信中使用的编码方案主要有RS码、低密度奇偶校验(Low Density Parity Check,LDPC)码和Turbo码等。ARIKAN在2008年提出的极化码[2]在近年来受到了极大的关注,在2016年的3GPP会议中表现出优越的性能,已经成为了5G方案中系统增强型移动带宽场景中控制信道的编译码方案[3]。由于极化码是基于信道特性构造的一种信道编码方案,因此在复杂场景中利用极化码作为信道编码方案能够表现出优越的渐进性能,同时其还具有其他编译码方案所不具备的低复杂度。虽然目前极化码属于信道编码领域的研究热点,但是在水下光通信等实际场景中的应用还非常少。

笔者首先利用了蒙特卡罗(Monte Carlo,MC)模拟算法追踪了光子的运动轨迹,并得到了3种不同水质条件下水下光通信所需的离散冲激响应。为了满足高速率的数据传输要求,建立了基于极化码的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)水下光通信系统,针对收发端已知的信道状态信息前提下,采用16正交幅度调制(16 Quadrature Amplitude Modulation,16QAM)方式,结合蒙特卡罗构造算法完成了极化码的构造,并使用了基于循环冗余校验(Cyclic Redundancy Check,CRC)辅助的串行抵消(CRC-Aided Successive Cancellation List,CA-SCL)译码算法完成了基于OFDM的水下光通信中的极化码方案的编译码流程。最后对比了相同码长条件下的LDPC码在不同信噪比(Signal Noise Ratio,SNR)条件下的性能,以此来证明极化码在不同水质条件的水下光通信中的性能优势,且在水质环境越差的条件下能够表现出更优越的渐进性能,另外还通过改变码长和译码宽度验证了不同参数对极化码在该信道下的影响。

2 极化码编译码原理

2.1 极化码编码原理

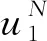
(1)

其中,GN表示极化码的生成矩阵。

2.2 极化码译码算法简述

(2)

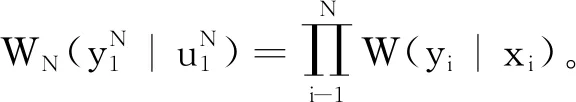
串行抵消译码列表(Successive Cancellation List,SCL)算法[4]是在串行抵消译码算法的基础上做了一定的改进,是一种广度优先的译码算法。在每一层的判决时保留最好的L条路径,L为译码宽度。SCL译码时会同时保留“0”和“1”两条路径,分别计算两条路径的度量,当路径数大于L时,保留置信度最高的L条路径并删除其他路径,在最后一个比特译码结束后,选择可信度最高的一条路径作为最终的译码数据并输出。

CA-SCL译码算法[5]是基于SCL译码算法改进而来的。CA-SCL译码算法是在SCL译码算法中对最后剪枝得到的L条路径进行CRC校验,再从通过校验的路径中选出最有可能的一条。由于使用该算法极化码的性能能够趋近最大似然译码的性能,因此选取CA-SCL译码算法作为译码方案。

3 基于MC模拟算法的水下光信道分析

目前对于水下光子的追踪和水下光通信系统的建立主要有解析法和MC模拟算法。解析法主要是对实际的光传输情况作近似处理,只能适用于限定的深度范围,而且利用其推导接收信号的数学表达式相当困难。与解析法相比,MC模拟算法具有较大的灵活性,可以应用于不同传输介质的组合中,且原理简单,计算方便。如1968年PLASS等[6]使用MC模拟算法计算了光在云层中的散射过程,系统地介绍了整个传输过程。1982年,LERNER等[7]利用MC模拟算法分析了激光在水下不同深度的角度分布和时域分布。2013年,GABRIEL等[8]利用MC模拟算法设计了水下数十米的通信系统,并考虑了光源、接收机等对误码率的影响。2018年胡思奇[9]利用MC模拟算法建立了跨介质和纯水下的信道模型,并研究了不同调制方式对水下长距离通信的影响。

3.1 基于MC算法的水下光信道模拟过程

利用MC模拟得到水下光子的运动轨迹,需要事先定义几个重要的参数:① 发射机参数,包括波长λ、光束宽度ω0和最大初始发散角θ0,max; ② 接收机和发射机之间的距离D;③ 接收机孔径大小和接收机视角FOV。MC模拟水下光信道冲激响应的具体算法步骤[8]如下:

(1) 初始化。光子的初始权重设置为单位权重,初始位置和初始发射方向可以使用3个随机变量来确定。初始位置根据U[0,1]确定(其中U[n,m]表示服从于n到m之间的均匀分布),初始方向由散射角θ和方位角φ确定,其中θ服从U[-θ0,max,θ0,max],φ服从U[0,2π]。

(2) 光子在海水中的随机散射。如图1所示,光子沿初始方向传输,在传输一段距离后可能会与水中的粒子相互作用而产生散射,这段距离可以称为随机步长(记为δ)。可以使用一个服从于U[0,1]的随机变量r来辅助生成步长δ,具体如下式:

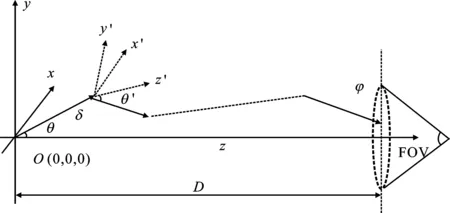
图1 光子与水中粒子相互作用散射图

δ=-ln(r)/c,

(3)

其中,c表示衰减系数。

(3) 光子的权重衰减。光子在经过与粒子的相互作用后还会发生权重的衰减,用Wpre和Wpost分别表示碰撞前后的光子权重,具体可用下式表示:

Wpost=Wpre(1-a/c) ,

(4)

其中,a表示吸收系数,c表示衰减系数。文中衰减系数c取决于吸收系数a和散射系数b,表示为c=a+b。由于不同的水质条件下的浮游生物等粒子数量不同,因此可以依据衰减系数等参数的取值差异,将水质类型分为纯净水、沿港水和浑浊水,具体如表1所示[10]。

表1 不同水质条件下的吸收系数、散射系数和衰减系数 m-1

(4) 更新光子方向。如图1所示,光子经过散射后会发生方向的偏移,需要更新其散射角θ和方位角φ。方位角φ可以直接由一个服从于U[0,2π]的随机变量表示。而散射角θ的更新需要根据水质条件来确定。文中使用一阶格林斯坦(Henyey-Greenstein model,HG)散射函数[11]来模拟光子散射,如下式所示:

(5)

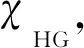
(6)

根据式(5)和式(6),θ可以表示为

(7)

(5) 接收端接收。如果光子到达接收面时光子权重大于10-4则接收,否则丢弃。另外,在仿真中没有限制FOV的值,即设置FOV=180°。

3.2 信道冲激响应

模拟接收和丢弃的光子的权重比例,并计算到达接收面之前光子走过的总路径,利用光速(≈2.26×108m/s,水下)可以将其转化为从发射机到接收机的传播时延。MC模拟算法本质上是统计学方法,需要依赖大量的光子进行模拟,所以文中生成了至少106个光子。

信道冲激响应是描述一个信道最有用的信息,其可以量化信号的衰减和时间色散。利用光子强度Ik来近似表示信道冲激响应,在这里把Ik描述为接收机在某一时间间隔内接收到的m个光子的权重WR的累加,如下式所示:

(8)

笔者在MC模拟算法仿真过程中,选择波长为532 nm的蓝绿激光,发射机参数中光束宽度ω0=3 mm,最大初始发散角θ0,max=20°,通信距离D=10 m,模拟了光子在3种不同水质条件下的散射过程,得到了其对应的信道冲激响应,具体表示如图2所示。在纯净水和沿港水条件下Ik下降得比较平稳,而在浑浊水这种复杂水质条件下,Ik出现了较大震荡,说明该水质条件对通信质量的干扰性最大。

图2 不同水质条件下的光子强度分布图

4 水下光通信系统模型

光信号在水下信道进行传输,在接收端接收到的信号yn可以表示为

yn=xnhn+vn,

(9)

其中,xn表示发送信号,vn表示方差为δ2的加性高斯白噪声(Additive White Gaussian Noise,AWGN),hn表示离散时间信道冲激响应,可以使用式(8)与Sa函数卷积得到,具体表示见下式:

(10)

其中,T为采样间隔。

为了满足高速率传输的要求,建立了基于OFDM的仿真系统,具体流程如图3所示。首先由发射机生成随机的二进制数据di,然后使用码率为1/2的极化码对数据进行编码,随后利用16QAM对编码好的数据进行调制,将调制好的16QAM符号映射到不同的子载波上,并在每8个子载波上插入导频,以实现对接收机的信道估计。最后利用快速傅里叶逆变换(Inverse Fast Fourier Transform,IFFT)将插入导频以后的调制符号Sk在时域上进行变换,得到的OFDM符号为

图3 基于OFDM的水下光通信系统流程图

(11)

其中,N为子载波数,k为子载波索引,n为时间序列。为了防止码间干扰和块间干扰的影响,在每个OFDM块的开头加入循环前缀(Cycle Prefix,CP),则发送数据表示为[12]

(12)

经过式(9)的水下信道衰减,在接收端经过移去CP和快速傅里叶变换(Fast Fourier Transform,FFT)操作后,将信号从时域转为频域,对其进行信道估计得到的复值信道频率响应表示为

(13)

其中,m表示第m个导频子载波,且Xp(m)=3+3j和Yp(m)分别表示发送和接收的导频符号。随后计算对数似然比(Log Likelihood Ratio,LLR)作为软信息用于极化码的构造和译码中,由于使用的16QAM调制,因此第1个比特b0的LLR的值为[13]

(14)

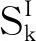
(15)

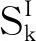
5 基于OFDM的水下光通信中的极化码构造

极化码的构造就是计算极化操作后各个子信道的可靠度,然后通过排序选择出可靠度最高的K位信息位索引。目前极化码的构造算法主要有二进制擦除信道(Binary Erasure Channel,BEC)构造、信道退化构造以及蒙特卡罗构造等。前两种方法分别适用于BEC信道和对称信道,而水下光信道是典型的非对称信道,因此文中选用蒙特卡罗构造来进行极化码的构造流程。

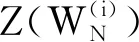
(16)

对于式(16)很容易看出Z(W)的取值范围为[0,1]。因此信道容量I(W)则有

(17)

当信道容量I(W)=1时,Z(W)=0;反之,当I(W)=0时,Z(W)=1。

蒙特卡罗构造是一种近似构造算法,可近似模拟子信道的巴氏参数,由式(4)可进行推导,具体见式(18):

(18)

综上,利用蒙特卡罗构造完成极化码的算法流程如下:

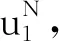
(2) 通过解调后,根据式(14)和式(15)计算每个对数似然比信息L(yi),并将其作为译码输入进行的SC译码,值得注意的是,此处的SC译码只是为了方便计算巴士参数,与文中使用的CA-SCL译码算法不冲突;

(4)排序挑选值最小的K个信道的索引构成索引集合,作为该信道信息位的选择方案。

由于极化码的构造是基于大量仿真得到的,为了保证整个仿真过程能够更加准确,本次实验进行了106次仿真。

6 仿真结果分析

6.1 极化码与LDPC码的性能比较

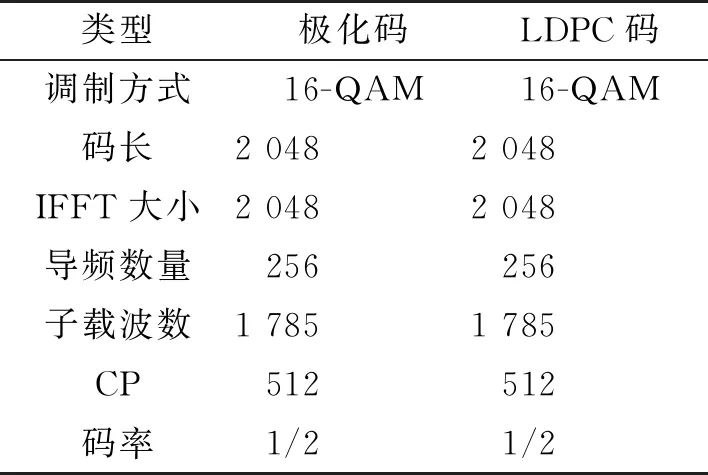
表2 仿真中使用到的主要参数

文中在仿真时用到的主要参数如表2所示。

根据仿真流程和表中数据进行了极化码的构造和译码,得到了3种不同水质中的性能结果,并与码长相近的LDPC码[13]进行了对比。

在纯净水条件下的性能曲线如图4所示,极化码在约4.1 dB以前时性能较差,在4.5 dB～5 dB时下降较快,在4.5 dB左右时性能已经超过了LDPC码。在沿港水条件下的性能曲线如图5所示,极化码在约6.5 dB以前时下降很慢,但是在约6.5 dB以后时下降速率远超未编码和LDPC码,而且当BER要求在10-3左右时,极化码比LDPC码的性能领先了约0.6 dB。在浑浊水条件下的性能曲线如图6所示,未编码方案在30 dB以前基本没有下降,同时极化码和LDPC码都下降得很慢,在24 dB以前,LDPC码的性能优势比较明显,但是随着SNR的增加,极化码的渐进性能优势明显地表现出来,而且从图中可以清晰地看出,LDPC码在29 dB～30 dB时曲线下降速率变慢,已经出现了误码平层的趋势,而极化码在后期的曲线下降速率越来越快,能够证明极化码在复杂水质条件下具有优秀的纠错性能和应用前景。

图4 纯净水条件下的性能曲线图

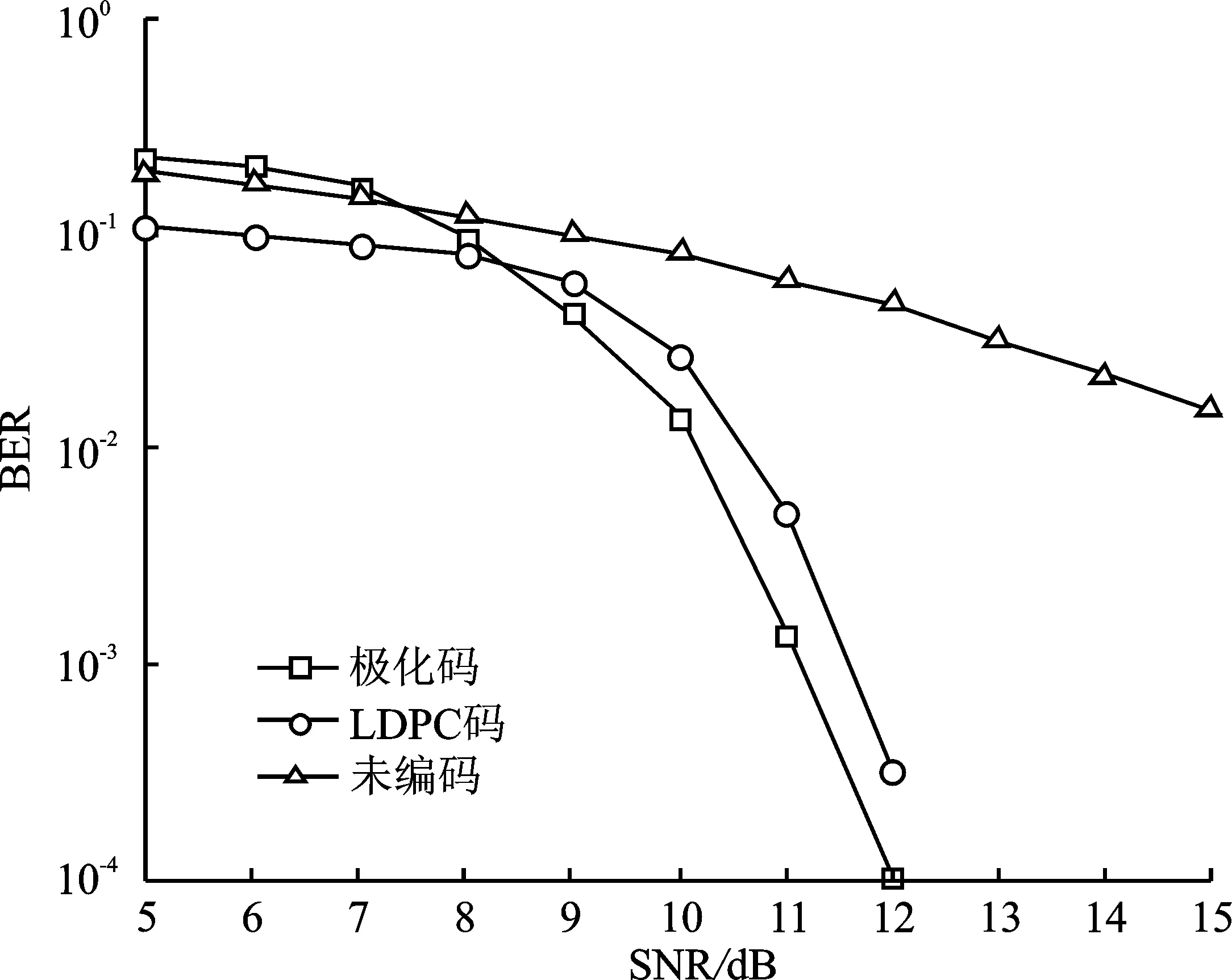
图5 沿港水条件下的性能曲线图

图6 浑浊水条件下的性能曲线图

综合来看,LDPC码在低信噪比时性能略优于极化码,这也符合LDPC码前期收敛速度快的优势,但是极化码的最大优势在于其译码的渐进性,因此随着信噪比的增加,极化码的性能优势会表现得越来越明显,且随着水质条件的变差其渐进性能表现得越明显,另外极化码不会出现LDPC码误码平层的问题,这一点在3种水质条件下的误码率性能图中均能明显看到。从仿真结果来看,使用纠错码方案能够大大提高水下光通信的性能,而且能够证明极化码在水下光通信中具有优越的自适应性和渐进性,与应用更广泛的LDPC码相比也具有一定优势。

最后针对两种纠错码的译码复杂度进行分析。假设两种码的码长均为N,LDPC码使用的BP译码算法的时间复杂度为O(N),极化码使用的CA-SCL译码算法的时间复杂度为O(NlogN),但是BP译码在实际使用中需要多次迭代,复杂度也会相应提高,而极化码的CA-SCL译码中只需一次遍历,不需多次迭代。综上所述,相比LDPC码,极化码的编码结构更加清晰简单,译码复杂度相差不大,且在译码中不需要多次迭代。

6.2 极化码的不同参数对系统性能的影响

6.2.1 不同码长对系统性能影响分析

为了分析码长对极化码在水下光通信中的性能影响,此处在不同水质条件下对不同码长的极化码性能进行仿真,码率均为0.5,且均使用译码宽度设置为8的CA-SCL译码作为译码方案。在保持上述相同的条件下,将极化码的码长分别设置为1 024和2 048,对不同码长极化码的误码性能进行仿真。

3种不同水质条件下的极化码的仿真结果如图7所示。由图可知,在纯净水条件下,当信噪比大于2.5 dB时,码长较长的极化码性能更优,当误码率要求在约10-4时,码长2 048比码长1 024有约0.5 dB的增益;在沿港水条件下也符合码长越长性能越好的性质,当误码率要求在约10-4时,码长2 048比码长1 024有约0.6 dB的增益;在浑浊水条件下依然符合该性质,当误码率要求在约10-4时,码长2 048比码长1 024有约0.6 dB的增益。

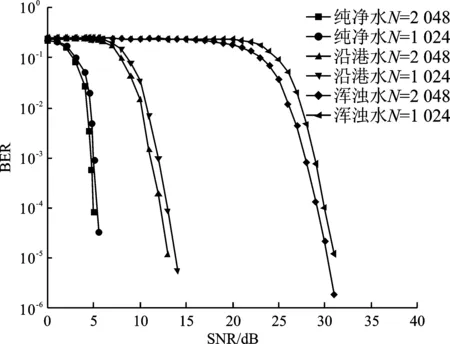
图7 不同码长对极化码性能的影响

综合来看,3种不同水质条件下的水下光通信均满足极化码码长越长性能越好的性质,且从图7中也能清晰地看到在水质条件更差的浑浊水中,随着信噪比的增加极化码的性能越好,且不会出现误码平层的现象。

6.2.2 译码宽度对系统性能影响分析

为了分析采用CA-SCL译码时译码宽度对极化码性能的影响,对采用不同译码宽度的极化码性能进行了仿真。极化码的码长均设置为2 048,码率均为0.5,采用CA-SCL译码作为译码方案。在保持上述相同的条件下,CA-SCL译码算法的译码宽度L分别设置为1、2、4和8。

在纯净水条件下,不同译码宽度的极化码性能仿真如图8所示,若误码率要求为10-2时,译码宽度为8的极化码相比于译码宽度为1的极化码约有0.8 dB的增益;相比于译码宽度为2的极化码约有0.35 dB的性能增益;相比于译码宽度为4的极化码约有0.15 dB的性能增益。在沿港水条件下,不同译码宽度的极化码性能仿真如图9所示,若误码率要求为10-3时,译码宽度为8的极化码相比于译码宽度为1的极化码约有1 dB的增益;相比于译码宽度为2的极化码约有0.6 dB的性能增益;相比于译码宽度为4的极化码约有0.25 dB的性能增益。在浑浊水条件下,不同译码宽度的极化码性能仿真如图10所示,若误码率要求为10-4时,译码宽度为8的极化码相比于译码宽度为1的极化码约有1.3 dB的增益;相比于译码宽度为2的极化码约有0.8 dB的性能增益;相比于译码宽度为4的极化码约有0.3 dB的性能增益。

综合来看,极化码的译码宽度越宽,系统的性能越好。这也符合文献[4]中不同译码宽度对于传统AWGN信道性能影响的结论,且从图8～图10中可以看出,水质条件越差,译码宽度对极化码的性能影响越大。

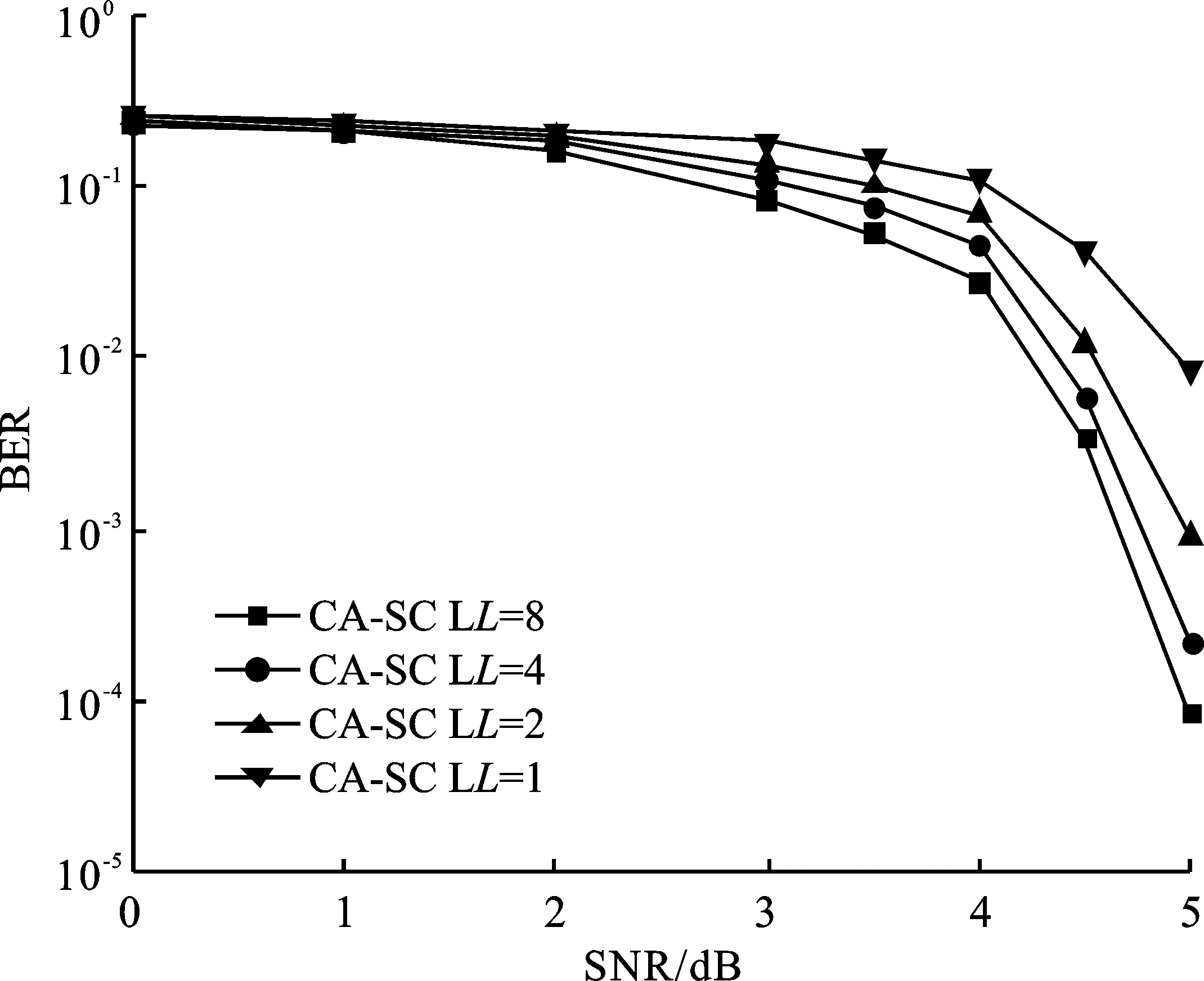
图8 纯净水下不同译码宽度对极化码性能的影响

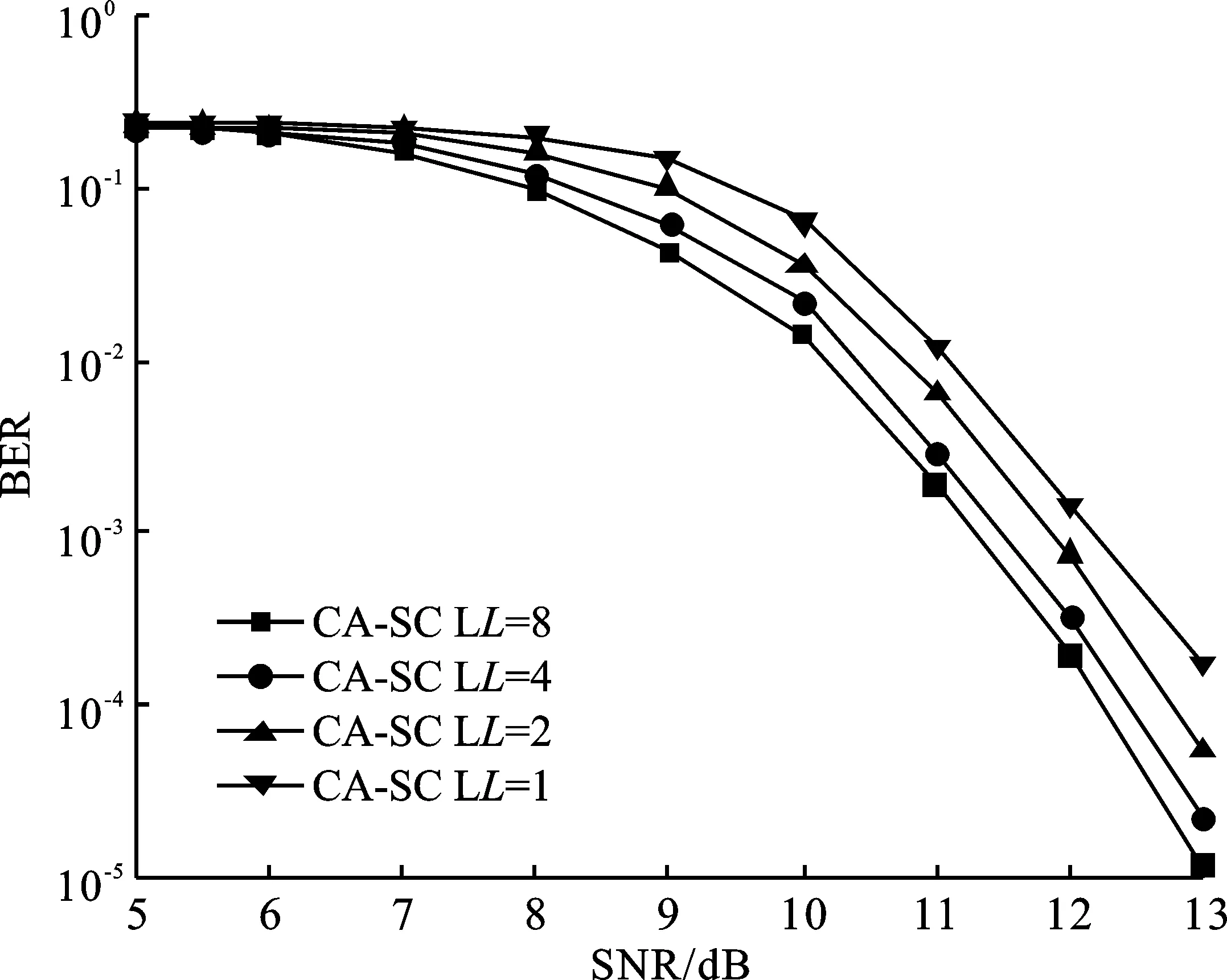
图9 沿港水下不同译码宽度对极化码性能的影响

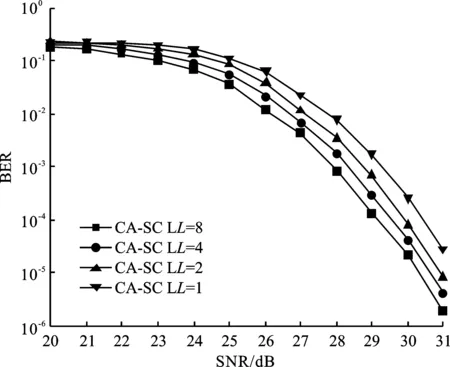
图10 浑浊水下不同译码宽度对极化码性能的影响

7 结束语

笔者利用MC模拟算法模拟了3种不同水质条件下的水下光信道的冲激响应,在此基础上建立了基于OFDM的水下光通信系统,将极化码和16QAM调制相结合,完成了极化码的构造和译码。通过仿真将极化码与码长相同的LDPC码在同等条件下进行了对比。仿真结果表明,使用编码方案能够显著地提高系统的误码率性能,同时在高信噪比条件下,极化码的性能优于LDPC码,能够获得更高的编码增益,表现出了优越的渐进性能。尤其在水质条件较差的环境中,极化码的性能优势更加明显,且不会出现误码平层的问题。此外,极化码的编码结构更加清晰简单,译码复杂度与LDPC码相差不大,且在译码中不需要多次迭代。因此采用极化码作为水下光通信场景中的编译码方案具有很强的竞争力和应用潜力。