并行传输编码缓存问题研究

2023-05-11林霄,罗松,刘楠

西安电子科技大学学报 2023年2期

林霄,罗松,刘楠

(东南大学移动通信国家重点实验室,江苏南京 211100)

1 引言

传统缓存技术通过提前在本地存储空间中缓存内容,获得本地缓存增益。如果本地存储空间有限,则对网络传输压力的缓解作用有限。不同于传统缓存技术,编码缓存技术[1]通过巧妙创造多播机会,使得服务器的一次广播传输能够同时满足多个用户的不同需求,从而得到了全局缓存增益。以文献[1]为基础,文献[2-8]从多个角度对编码缓存问题模型进行变形,继续研究编码缓存相关问题。除了服务器通过共享链路向多个用户发送信息的形式,用户之间也可以发送信息,当编码缓存技术应用在D2D(Device-to-Device)网络,可以在没有服务器的情况下,得到几乎与服务器多播编码缓存方案相同的增益。许多研究针对D2D网络中的编码缓存问题进行了研究[9-18]。

考虑到用户之间可以互发信息的同时,服务器也能够向所有用户发送信息的实际应用场景,有研究提出了并行传输的编码缓存问题模型,并提出一种并行传输的缓存与交付方案,得到了用户协作增益和服务器编码多播增益,并证明了该方案传输速率的可达上界与下界之间存在常数间隔。然而,在实际场景中,更为常见的情况是接入网络的用户设备多种多样,用户中可能同时存在手机、电脑、服务器等。由于物理条件的限制,它们各自的存储空间大小也各不相同。同时在实际应用中,信道传输能力不同的情况也更为普遍。因此,目前对于并行传输编码缓存问题的研究具有一定的局限性。针对以上问题,有必要开展在更符合实际应用场景的信道传输能力不同的场景下,基于服务器与用户都能够发送信息的情况,对并行传输编码缓存问题展开研究。

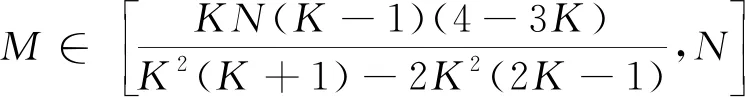
2 并行传输编码缓存问题模型

考虑一个服务器,通过一个无差错广播信道连接K个用户,每个用户都具有存储空间。服务器端存储N个文件,W1,…,WN,每个文件具有F个比特。用户k的缓存空间大小表示为MkF,k∈[K]。文中考虑所有用户的缓存空间大小相同的情况,即M1=M2=…=MK,统一用M表示,M∈[0,N]。

整个网络由服务器和用户构成,如图1所示。合作网络的特征总结如下:① 用户端可以同时接收来自服务器和其他某个用户的信息,这是因为两个传输过程发生在不同频带,互不影响;② 如果在某一时刻,某个用户正在发送信息,那么与此同时,他将无法收到来自其他用户的信息。

图1 并行传输编码缓存问题模型

连接服务器和K个用户的广播信道的信道容量由Cs表示,描述了该信道的最大传输能力。同时,用户之间也具有互相发送信息的能力,用户之间通信的信道容量由Cu表示,描述了当用户轮流向其他用户发送信息时的传输能力。Cs和Cu的单位均为比特每秒。当网络中出现通信任务,需要关注的指标为完成交付任务的传输延时,单位为秒。

2.1 函数定义

整个通信过程描述如下:在出现文件请求任务之前,每个用户都可以接触到服务器端的所有文件,并用这些文件来填充自己的缓存空间。用户k,k∈[K]通过缓存函数φk,将W1,…,WN映射到大小为Mk的缓存空间中,缓存内容为Zk,即

Zk=φk(W1,…,WN) ,

(1)

共有K个缓存函数:

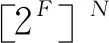
(2)

当每个用户k都存在一个文件请求,即Wdk,所有用户的请求都会同步到服务器和各个用户。当服务器和所有用户都得知文件请求向量d后,会进行文件编码。首先,服务器根据其拥有的N个文件,编码得到待传输的信息:

Xs=fd(W1,…,WN) ,

(3)

其中,编码函数为

(4)

每个用户会基于其预先缓存的内容Zk进行编码:

Yk=gk,d(Zk) ,

(5)

编码函数gk,d为

(6)

其中,Rs表示由服务器传输的数据量,也称为服务器的传输速率;Ruk表示用户k传输的数据量,即用户k的传输速率,单位均为比特。

传输阶段结束之后,用户k分别收到来自服务器和其他用户的信息,并根据所收到的信息,得到所请求的文件:

(7)

Y1,…,Yk-1,Yk+1,…,YK表示用户k收到的来自其他用户的信息,解码函数为

(8)

定义差错概率为

(9)

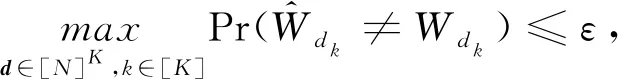
2.2 性能指标

服务器的传输和用户之间的传输可以同时进行,因此定义传输延时T:

T=max(Ts,Tu) 。

(10)

最优的传输延时T*定义为

(11)

3 主要结论

(12)

4 可行方案

4.1 实现方案

(1) 第1阶段:预缓存

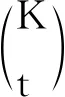
(13)

(2) 第2阶段:分配

(14)

对于此时再次划分后得到的更小的子文件,用上标l∈[L1+L2]来描述:

(15)

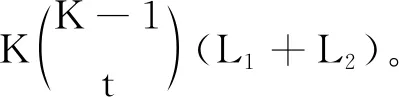
(3) 第3阶段:交付

对于用户k,k∈[K]的请求dk,用户仍需从外界获得的子文件为

(16)

其中,由服务器负责传输的子文件为

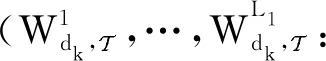
(17)

由用户负责的子文件为

(18)

(19)

接下来,考虑由服务器进行的传输。这一部分的实现使用了与文献[1]相同的传输策略,服务器传输

(20)

因此,得到由服务器传输得到的传输延时为

(21)

整个通信网络的传输延时为T=max{Ts,Tu},由式(14)、式(19)及式(21)可以发现Ts=Tu,此时的传输延时T为

(22)

与定理1中所描述的可达上界TC一致。

4.2 性能对比

文献[1]介绍了由服务器进行传输的中心化预存储编码缓存方案,文献[11]介绍了D2D网络中的编码缓存交付方案。图2对比了当Cs=1,Cu=5时,这两种实现方案与文中方案中用户缓存M与传输延时T之间的关系。可以看出,文中所提出的编码缓存方案相比于文献[1]和[11],传输延时减少。由于此时D2D网络信道的传输能力强于服务器广播信道,因此与文献[1]中可达交付方案相比,文献[11]中的可达交付方案具有明显的性能提升,但文中所提出的交付方案依然可以实现比以上两种已知交付方案更短的传输时长,尤其在用户缓存空间较小的情况下。

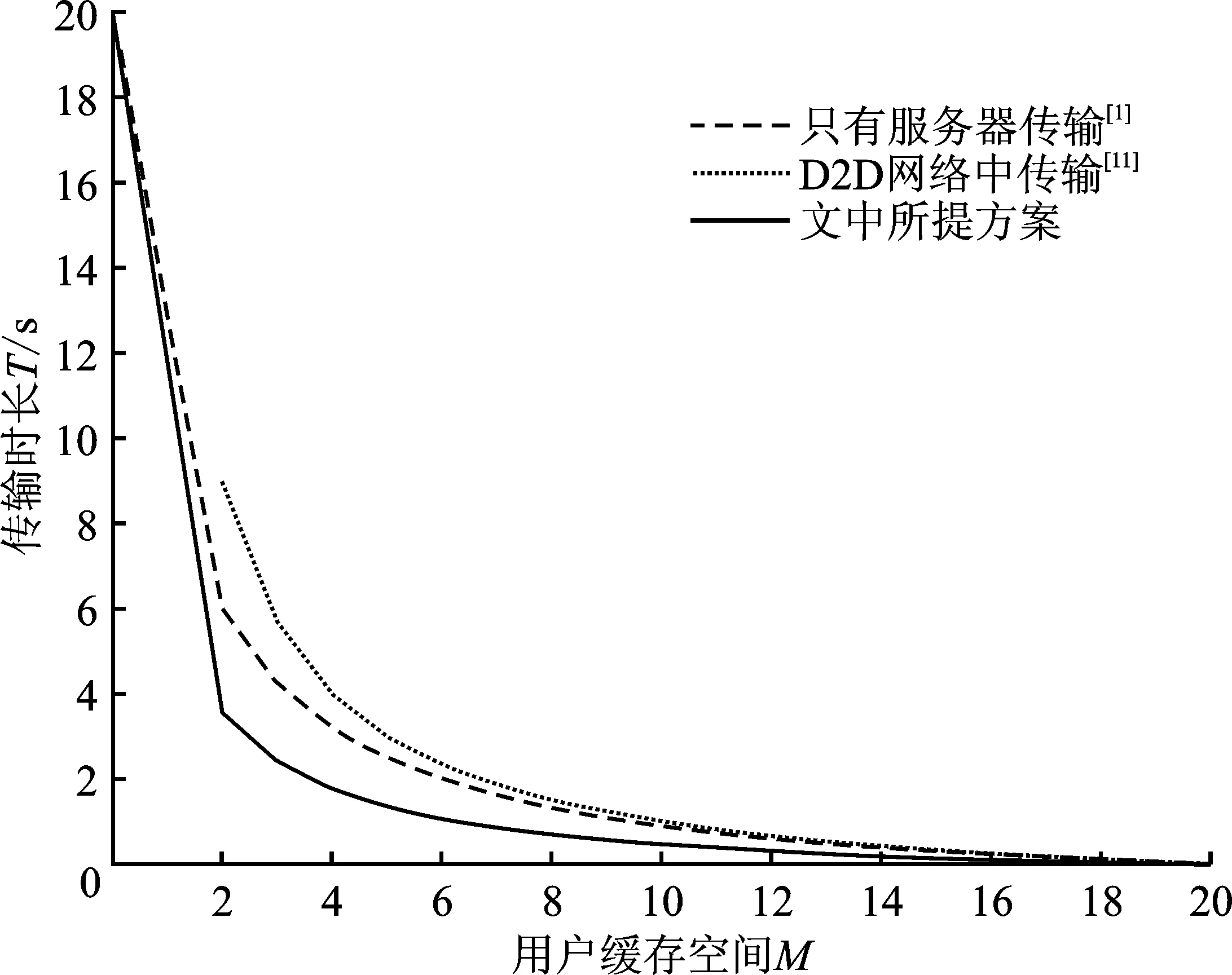
图2 当K=20,N=20,Cs=1,Cu=5时,不同实现方案的性能对比

图3将文中所提方案与文献[18]中的缓存交付方案进行对比。对比了当文件数N,用户数K一定时,使用这两种方案进行并行传输编码缓存,最终传输时长与用户缓存空间大小M之间的权衡。可以看出,当服务器广播信道和D2D网络信道的传输能力不同时,与使用了文献[18]中方案相比,文中提出的缓存交付方案存在明显性能提升,尤其在用户缓存空间较小时,性能改进效果明显。同时两种信道的传输能力差距越大,文中案对性能的提升就越佳,笔者所提缓存交付方案优势更大。

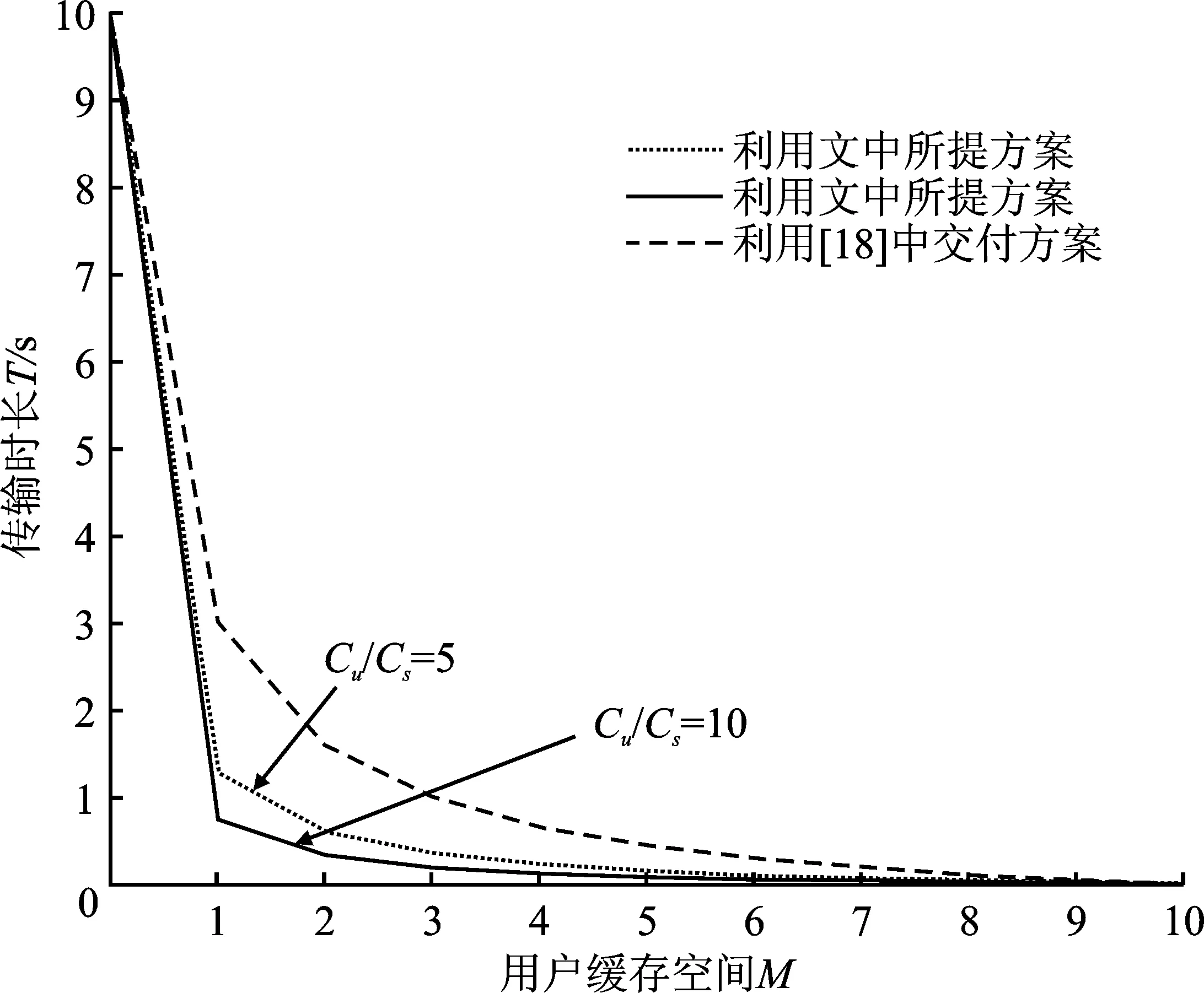
图3 当K=N=10时,不同实现方案的性能对比

5 最优性分析

5.1 准备工作

本节对最优性证明过程中需要用到的相关引理进行阐述。

引理1在具有一个中央服务器和K个用户的并行传输编码缓存网络中,Xs为服务器多播的信息,Rs表示服务器传输信息量大小,Yi表示用户i发送给其他用户的信息,i∈[K],Ru为所有用户组成的合作网络中所传输的总信息量,则有

(23)

其中,[K]/{i}表示K个用户中除去用户i以后的用户集合。引理1描述了为令所有用户都可以恢复出其所请求文件,服务器多播速率Rs和D2D网络内部传输速率Ru需要满足的下界条件。

接下来,与文献[19]类似,定义aj,{1,…,K}表示一个包含了F个比特的文件在用户集合{1,…,K}中的j个用户中缓存的比特数量,即

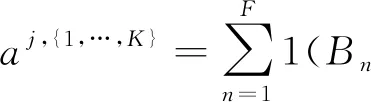
(24)

其中,F为一个文件的大小,单位为比特;Bn表示文件的第n个比特;Kn表示缓存了Bn的用户集合。

根据aj,{1,…,K}的定义,有以下结论。

引理2考虑N个大小为F比特的文件,将其缓存到K个用户的缓存空间中,aj,{1,…,K}定义见式(24)。那么有

(25)

(26)

引理3在具有一个中央服务器和K个用户的并行传输编码缓存系统中,Xs表示由服务器广播的信息,Yi表示用户i发送的信息,i∈[K]。aj,{1,…,K}根据式(24)定义,那么有

(27)

引理3描述了除了用户所请求的Wdi和用户已缓存内容Zi以外,其收到的来自服务器与其他用户的信息量的下界。此下界以比特数量aj,[K]的形式表示。

5.2 K=N=3时的最优性分析

为便于理解最优性分析思路,以K=N=3的情况为例,说明最优性的证明过程。文中提出的非编码预存储并行传输的编码缓存方案中,服务器会向所有用户发送信息,信息量以Rs表示,同时用户之间可以相互发送信息,合作用户网络中发送的总信息量为Ru。由于考虑的是两种信道传输能力相同,且Cs=Cu=1的情况,因而此时传输时长Ts=Rs/Cs=Rs,Tu=Ru/Cu=Ru。将二者中的最大值作为整个编码缓存模型的传输时长,即T=max{Ts,Tu}。后文将统一使用R、Rs和Ru进行证明。

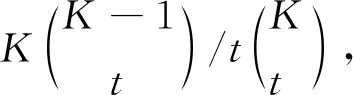
当考虑M、Rs和Ru三者之间的关系,以点(M,Rs,Ru)表示。定义Conv(ct),t∈{1,…,K}为所有可行解组成的包络。接下来,如果能够证明:Conv(ct),t∈{1,…,K}中,存在恰好也是传输信息量R的下界的部分,即当给定K和N,存在这样的用户缓存空间大小M,使得此时的并行传输编码缓存方案的实现速率满足:

R≥Conv(ct) ,

(28)

那么就意味着当用户缓存空间大小M属于这部分时,所提非编码预存储并行传输编码缓存方案的可达速率与速率下界匹配。当用户缓存空间大小M满足以上条件时,所提实现方案是最优的。

图4 K=N=3时,可行解组成的上界包络Conv(ct)

3Rs+2Ru+M=3 ,

(29)

3Rs+2Ru+2M=5 。

(30)

接下来,证明

3Rs+2Ru+M≥3 ,

(31)

3Rs+2Ru+2M≥5 ,

(32)

就能够说明在这两个平面所对应的用户缓存空间范围中,定理1对应的非编码预存储的并行传输方案的最优性。接下来,将针对式(31)和式(32)分别证明。

5.2.1 式(31)的证明

当K=3时,利用引理1得到

(33)

接着,将式(33)中的下界继续缩小:

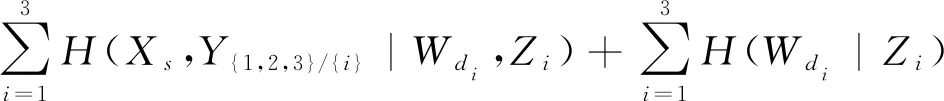
(34)

(35)

其中,Wdi表示用户i的请求,Zi表示用户i缓存的内容,i∈[K]。

注记1:(a)是由于H(Xs,Y{1,2,3}/{i}|Wdi,Zi)≥0,但此时的下界并不一定总是紧的。已知t代表了每个子文件在用户缓存空间中重复缓存的次数,当每个子文件都在K或(K-1)个用户中预缓存,在本例中,即2≤t≤3时,总会存在一个实现方案使H(Xs,Y{1,2,3}/{i}|Wdi,Zi)=0成立。此时,式(35)得到的下界是紧的。

(36)

其中,(b)基于aj,{1,…,K}的定义,(c)是由于

(d)由引理2可以得到。

由式(33),式(35)和式(36),有3Rs+2Ru+M≥3,则式(31)证明完毕。

5.2.2 式(32)的证明

在关于式(31)的证明中,式(33)不等号右侧的下界缩小为式(34)后,由于H(Xs,Y{1,2,3}/{i}|Wdi,Zi)≥0且在2≤t≤3时有H(Xs,Y{1,2,3}/{i}|Wdi,Zi)=0,因此式(35)得到的下界是紧的。

(37)

发现

3a0,[K]+a1,[K]=(3a0,[K]+2a1,[K]+a2,[K])-(a1,[K]+a2,[K])=

(38)

由式(34)、式(36)～(38)可以得到

3R1+2R2(3-M)+(2-M)=5-2M,

(39)

式(32)证明完毕。

图5 K=N=3时最优的上界包络Conv(ct)

5.3 任意用户数K和文件数N时的最优性分析

在这一部分,将说明任意用户数K和文件数N情况下,如何应用节4.2所述证明方法来证明所提非编码预存储并行传输编码缓存方案的最优性。

在节4.2K=N=3的情况下,证明了Conv(ct)中,M取值最大的两个平面的最优性。当任意K、N时,t∈{1,…,K},Conv(ct)由t+1个平面组成。所有可行解组成的包络Conv(ct)的多个连续平面中,M取值最大的两个平面表示为

(40)

(41)

同时,在节4.2证明过程中用到的引理1、引理2和引理3都是在任意K、N的条件下成立的,因此在任意K、N的条件下,依然可以利用引理1、引理2和引理3进行证明。

下面将说明任意K、N时,如何证明以上两个平面所代表的非编码预存储并行传输方案的可行解的最优性。

5.3.1 式(40)的证明

当M=N时,此时用户可以在各自缓存空间中缓存完整的数据库内容,无需进行信息传递,R=Rs=Ru=0,即点(N,0,0)是非编码预存储并行传输方案的可行解。当M=(K-1)N/K时,此时t=K-1,同样先考虑两种极端情况:Rs=0与Ru=0,此时点((K-1)N/K,1/K,0)和((K-1)N/K,0,1/(K-1))同样为非编码预存储并行传输方案的可行解。以上3点构成了Conv(ct),t∈{1,…,K}包络中的第一个由可实现点组成的面:

(42)

根据引理1,得

(43)

将式(43)中的下界继续缩小,得到

(44)

(45)

其中,Wdi表示用户i的请求,Zi表示用户i缓存空间中缓存的内容,i∈[K]。