加权分数傅里叶辅助的上行NOMA隐蔽通信
2023-05-11段正祥张兆林
段正祥,杨 欣,张兆林,王 伶
(西北工业大学 电子信息学院,陕西 西安 710072)
1 引 言
随着无线移动通信的快速发展和通信设备的小型化、低成本化,无线终端和敏感信息(如身份认证、健康状况)的数量也快速增加,使得有限的频谱资源更加拥挤。非正交多址接入(NonOrthogonal Multiple Access,NOMA)可以有效地提升频谱效率,是大规模多用户接入中一项很有前途的技术[1]。然而,由于无线信道的开放性,给信息安全带来了问题。为了解决这个问题,近年来有许多关于物理层安全的研究[2-4]。物理层安全仅仅关注如何保护通信的信息不被窃取,而在某些场景中暴露通信行为也会带来风险,如一旦被发现正在通信,便可能遭受无线网络攻击或被定位。因此,现在有越来越多关于非正交多址接入系统中隐蔽通信的研究,它可以最大化监听者的检错概率。

上述提到的方法主要集中在如何产生干扰去影响Willie的判断,并且都假设两种假设的先验概率相等。现有的文献中也缺少Willie如何获得先验信息的研究。根据上述讨论,首先对一个存在两阶段检测器的上行非正交多址接入系统,提出了采用随机功率分配和WFRFT方案来实现隐蔽通信,即最大化Willie的检错概率。两阶段检测器由能量检测和相似度检测两个阶段构成,其中能量检测阶段用来判决是否存在隐蔽通信,相似度检测阶段通过检测信号与噪声的相似度为能量检测阶段提供先验概率。其次,提出了随机功率分配和WFRFT方案来混淆Willie的决策。对于提出的方案,给出了期望最小检错概率、可靠用户和隐蔽用户的中断概率的闭合表达式。为了优化可靠用户的功率分配,在隐蔽约束和可靠约束下分析了最大期望隐蔽速率。数值仿真结果表明,所提的两阶段检测器有更低的期望检错概率,而随机功率分配和加权分数傅里叶变换方案也提升了系统的隐蔽性能。
2 系统模型
2.1 通信场景
如图1所示,给出了一个上行功率域非正交多址接入的隐蔽通信场景。该场景中包括了一个隐蔽用户CU,一个可靠用户RU,一个接收机Bob和一个被动监听者Willie。RU和CU有不同的通信需求,RU期望可靠传输,即保障通信速率,而CU尝试传输私密信息而不被人发现,即最大化Willie检错概率。因此,假设RU是NOMA系统中的高信噪比用户,而CU是低信噪比用户。Willie在不断检测CU的通信状态,并试图拦截CU传输的信息,但不会干扰CU和RU的传输,而CU和RU通过合作来混淆Willie的探测。网络中的每个节点都配备了一根天线。
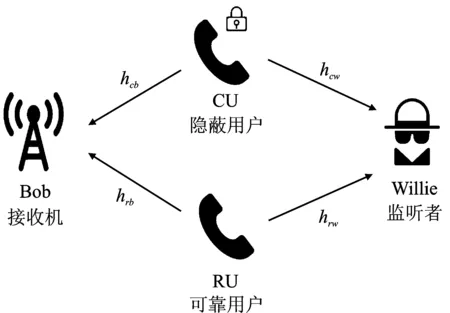
图1 上行功率域NOMA隐蔽通信场景图
假设所有信道都经历了准静态块瑞利衰落,即信道系数在一个时隙中保持不变,而从一个时隙到另一个时隙独立变化。定义节点i到节点j的信道表示为hij,其中i及j∈{r,c,b,w},r,c,b和w分别表示RU,CU,Bob和Willie。|hij|2的期望表示为E(|hij|2)=1/λij,其中λij表示信道衰减系数,E(·)表示求期望。考虑一种最坏的情况,即Willie拥有hrw和hcw的信息。
2.2 传输策略
RU采用了随机功率分配来辅助CU进行隐蔽传输。RU的传输功率Pr在每个时隙都发生变化,并且服从区间[Pmin,Pmax]中的连续均匀分布,概率密度函数可以表示为
(1)
其中,Pmin和Pmax分别代表RU的最小和最大发射功率。Pmax受限于硬件,因此无法改变;而Pmin可以调整。为了混淆Willie的判断并且传输更多的信息,RU在持续进行通信。如此,当Willie检测到接收功率提升时,既可能由于CU开始进行通信,也可能由于RU的发射功率增大。CU的发射功率设置为一个定值Pc。为了进一步混淆Willie的判断,CU采用了4项WFRFT[14],其传输符号形式表示为
xc[i]=w0(α,V)sc[i]+w1(α,V)Sc[i]+w2(α,V)sc[-i]+w3(α,V)Sc[-i] ,
(2)
其中,i=1,…,k,代表信道使用的索引;Sc[i]=F(sc[i]);F(·)代表傅里叶变换;α代表变换阶数;V代表尺度矢量,V=[MV,NV],MV=[m0,…,m3]与NV=[n0,…,n3]均为整数向量。第l(l∈{0,1,2,3})个加权系数表示为
(3)
CU可以通过调整4项WFRFT的参数改变传输波形,从而扰乱Willie的判断。
2.3 检测策略
为了降低Willie的检错概率,提出了一种两阶段检测策略,包括能量检测和相似度检测两个阶段。在能量检测阶段,Willie使用辐射计来检测CU是否在传输隐蔽信息;在相似度检测阶段,Willie通过计算估计的CU信号幅度分布与噪声的相似度来估计两种假设的先验概率。Willie的检错概率定义为
(4)
其中,PFA和PMD分别代表能量检测阶段得到的虚警概率和漏检概率,κ代表在相似度检测阶段得到的隐蔽传输不存在的先验概率。
能量检测阶段:在零假设H0(隐蔽传输不存在)和备择假设H1(隐蔽传输存在)下,Willie的接收信号表示为
(5)
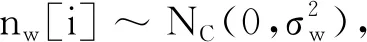
辐射计表示为
(6)
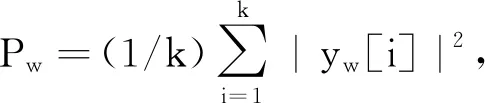
(7)
相似度检测阶段:为了降低检错概率,所提方案会对两种假设的先验概率做出估计。由于RU在持续传输信号,可以假设Willie已知RU的信号的分布,同时信道hrw和hcw的统计信息也已知,因此Willie可以根据上述信息估计CU信号的幅度分布。常见的调制信号,例如相移键控(Phase Shift Keying,PSK)和正交幅度调制(Quadrature Amplitude Modulation,QAM),其幅度分布在几个固定的值上,如图2所示,因此可以通过估计的CU信号的幅度分布去估计两种假设的先验概率。在H0和H1下估计的CU信号为

图2 不同阶QAM信号幅度概率密度分布及拟合瑞利分布示意图
(8)
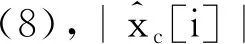
相似度计算步骤如下。
第1步 为方便幅度分布统计,采用离散概率密度分布函数,表示为
(9)
其中,Δ表示离散值的间隔;x=kΔ+Δ/2,表示每个区间的中值,k∈N;P(·)表示计算概率。
(10)
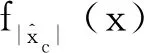
(11)
(12)
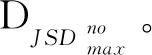
(13)
可以看出κ∈[0,1]。
对先验概率的了解可以提高Willie的检测性能[5]。Willie在相似度检测阶段,估计了CU的传输状态而不是完全随机的猜测,因此所提的两阶段检测方案可以减少Willie的检错概率。注意相似度检测阶段并不会直接对是否存在隐蔽通信进行判断,只是为能量检测阶段的门限设置提供参考,最终决策由辐射计得到。
3 隐蔽性分析
在本节中首先给出了Willie的最佳检测门限和相应的最小检错概率;其次,考虑到通道的不确定性,从CU和RU的角度计算Willie的EMDEP;最后,给出了WFRFT中参数α与κ的关系。
3.1 最优门限设置
引理1Willie的最佳检测门限是
(14)
其对应的最小检错概率为
(15)
证明 根据检错概率的定义,PE为

(16)

(17)
根据式(17),可得最佳检测门限和相应的最小检错概率。证毕。
从RU和CU的角度,最优的波形既不完全像噪声也不完全不像噪声。从式(15)可得,当介于这两种情况之间时,即κ=0.5,最能够混淆Willie对先验概率的判断。
3.2 期望最小检错概率

引理2在最佳检测门限下,Willie的期望最小检错概率为
(18)
证明 当ν12>ν21,κ<1/2时,根据期望计算公式,可以得到
(19)
步骤(a)可根据文献[16]中的积分公式3.411.19.9得到。
对于κ≥1/2的情况,推导过程相似。证毕。
3.3 加权分数傅里叶的噪声相似度
考虑一种最不理想的情况。假设当隐蔽传输存在时,Willie能够准确地估计出CU信号的幅度分布。由式(2)可以看出,4项WFRFT是两项时域信号和两项频域信号相加,其中时域信号分布于固定的星座点上。根据中心极限定理可得,当进行离散傅里叶变换的点数趋近无穷时,变换后信号的同相分量与正交分量也趋近于高斯分布,这也表明信号接近于噪声。因此,可以通过调整每一项的加权系数wl(α,V)来调整WFRFT后信号与噪声的相似度。从图3可以看出,QPSK标准星座图随着参数α变化会出现旋转、弥散、分裂和混淆的现象,这不仅实现了信号隐藏,并使信号波形变得可控。

(a) α=0,V=0
图4给出了不同参数α下1 024个QPSK符号经过WFRFT后的κ值。根据式(3)可知,α越接近1或3,变换后的频域项占比越大,波形也越加接近噪声,因此κ值越接近1;反之亦然。当κ最接近0.5时,能在Willie产生最大的不确定性。因此,在后续的分析中取α=2.1,此时κ=0.53,且xc[i]中sc[-i]及Sc[-i]两个倒序序列占比最大,也进一步增强了安全性。

图4 PSK符号经过不同参数α的WFRFT后κ值曲线图
4 可靠性分析
利用中断概率来衡量隐蔽通信的可靠性,分析了当隐蔽传输存在时RU和CU的中断概率。此外,还分析了隐蔽约束和可靠约束下的最大期望隐蔽速率。
4.1 RU和CU的中断概率
在H1下,Bob接收的信号为
yb[i]=(Pr)1/2hrbxr[i]+(Pc)1/2hcbxc[i]+nb[i] ,
(20)

注意,为了满足RU的可靠性,Bob接收到的RU信号信噪比应当高于CU信号信噪比。根据上行非正交多址接入的串行干扰消除策略,RU信号应当首先被译码,此时CU信号被当作干扰。之后,Bob将RU信号从总信号中去除,并译码CU信号。因此,如果RU信号发生中断,那么CU信号也无法被正确译码。Bob处RU信号的信干噪比表示为
(21)
Bob译码CU信号的信噪比表示为
(22)
其中,μr=2Rr-1,Rr是预设的RU通信速率。
引理3RU到Bob的中断概率为
(23)
证明 根据中断概率的定义,Or表示为
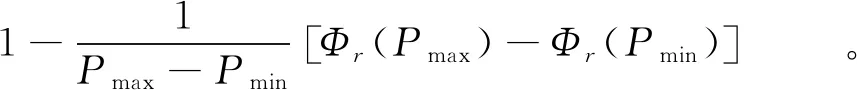
(24)
Φr(x)表示为
(25)
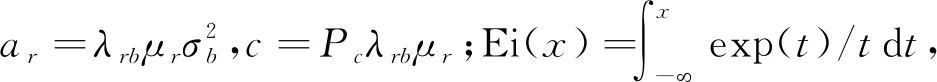
求解Or关于Pmin的偏导可以得到,当0 引理4CU到Bob的中断概率表示为 (26) 证明 与Or相似,Oc表示为 (27) (28) 与Or相似,当0 (29) 图7 不同隐蔽约束ε下RU中断概率Or和期望隐蔽速率与CU发射功率Pc的关系图 以上研究了一个存在两阶段检测器的上行非正交多址接入系统,提出了采用随机功率分配和WFRFT方案来实现隐蔽通信。首先在Willie处设计了一种两阶段检测器,其中一个阶段是能量检测,用于判断隐蔽传输是否存在;另一个阶段是相似度检测,检测信号与噪声之间的相似性,为能量检测提供先验信息,从而降低检错概率。接着为了应对能量检测和相似度检测阶段,分别在RU和CU采用了随机功率分配和WFRFT。然后,推导了期望最小检错概率、RU和CU的中断概率的闭合表达式。最后为了优化可靠用户的功率分配,在隐蔽约束和可靠约束下,分析了最大隐蔽速率。数值结果表明,所提检测方法有更低的检错概率,采用WFRFT后也提高了隐蔽性。 在未来的工作中,将对MIMO-NOMA系统中的隐蔽通信进行研究。
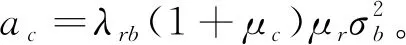
4.2 隐蔽通信设计


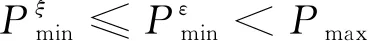
5 数值结果

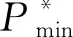

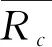

6 总结与展望
