模糊空间下双标签指纹定位算法

郑安琪,秦宁宁

(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)

1 引 言

全球导航卫星系统(Global Navigation Satellite Systems,GNSS)的不断成熟,极大地支撑了室外场景丰富的定位应用。但建筑物遮挡导致卫星信号被遮蔽,室外通用的卫星定位技术,显然无法简单地移植到复杂的室内定位场景中,尤其在精度、稳定性、时效等性能方面难以得到保证。因此,低误差、高可靠的室内定位技术成为了定位导航领域的一个研究重点。随着室内WiFi信源的广泛部署与智能移动设备的普及应用,以信号强度为导向的指纹定位算法,由于其高成本效益与对环境的普适性特征,已成为最常用的方法之一[1]。该方法在离线阶段,完成对各参考点(Reference Point,RP)位置的标记以及对其可见接入点(Access Point,AP)接收信号强度(Received Signal Strength,RSS)的样本采集和分析处理,构建指纹库[2]。在在线阶段,将待定位点实时接收的RSS向量与离线指纹库样本进行匹配,实现目标的空间位置估计。

传统的指纹定位方法,通常是将待定位点与指纹库中参考点依次进行相似性匹配,在带来高计算量的同时也导致定位精度受参考点分布影响较大。为降低计算负担与提高定位精度,聚类算法被引入指纹定位中。离线阶段对指纹数据库进行簇群化处理,如k-means[3-4]、模糊C均值(FCM)[5]以及仿射传播聚类(APC)[6]等方法,将整个目标区域划分为多个子区域,利用簇类切分形式实现在线阶段簇群匹配,以待定位点与所属簇群内参考点的相似度匹配替代全局比对过程。但不同于单纯的数据聚类处理,作为数据通道的无线信道,具有不可预测的动态衰减、多径效应等特征,导致指纹信息难以具有绝对清晰的簇间边界,簇间过渡区对于边缘点信息归属误判的影响明显。

除离线聚类因素外,在线匹配对于定位的有效性,也起着至关重要的作用。加权K近邻算法(WeightedK-Nearest Neighbor,WKNN)[7]通过计算待定位点与指纹库中相似度最高的K个近邻参考点的加权质心实现位置估计,但对于目标移动、障碍物变化、接入点状态改变等环境特性考虑欠缺;固定的K值和分散的指纹点选取,也将无法避免遗失重要空间信息甚至引入虚假离群点的问题[8]。为适配环境的动态变化,以多目标优化构建准则模型[9],实现对在线接入点的自适应筛选;或者通过参考点排序[10],削弱相似度判断标准的不稳定,但此类方案均缺乏信号动态差异对定位影响的考虑。为应对参考点固定选取无法适应指纹动态变化的不足,王培重[11]基于动态K值概念,去除欧式相似度小于阈值的指纹点来保证一定的定位精度,但仍无法确保离群点筛除;TAO[12]通过单独处理来自每个接入点的接收信号强度,强化近邻点位置的集中,但算法时间复杂度较高,实时性无法得到保证。

为解决簇间边界模糊、环境和信号动态特性对指纹定位结果的交叉干扰问题,笔者提出了一种模糊空间下双标签指纹定位算法(Dual-Label fingerprint localization algorithm in Fuzzy Space,DLFS)。以参考点“类间-类内”的双距离差异,刻画待定位场景过渡区域的模糊度,寻求区域判别精度和时间代价之间的平衡;将区域重叠分布上的增益效果,辐射影响到在线待测点位置估计,结合指纹排序弱化参考点匹配误差,利用指纹信号域和空间域迭代约束近邻点集合。这种模糊划分机制可以有效减少定位匹配工作量,在重新定义相似度判断标准的基础上,实现最佳近邻点的自适应选择,降低了近邻点空间位置分散和固化近邻集合对定位结果的不利影响。

2 系统模型

3 离线划分

3.1 平面空间分类

通过区域划分,可以有效缩小最佳定位点的寻找范围。但以指纹点与聚类中心距离作为参考点划分唯一依据,极有可能导致在线阶段待定位点的分区误判。经典k-means方法通常基于信号域均值相似性,以迭代化方式划分空间,收敛速度快且聚类效果良好,但对于信号稳定性较差的过渡区域,其参考点最小信号域距离并不一定能映射最小空间域距离,这一冲突在拐角、廊形等复合空间结构中,表现更加明显。

如图1(a)中场景采用“一刀切”式非此即彼的硬聚类模式,该方法简单直接,但很容易使得位于簇间边界的待定位点TP1存在分类尴尬,甚至导致位于簇Ωs边缘地带维稳能力相对较弱的待定位点TP2被错误归属到近邻簇Ωt中。与之相比,软聚类模式则允许样本同时归属于多个原型。综合考虑样本点簇间相似性的误判过程,在原“单一”区域基础上,对于过渡区域增设具有弱化边界绝对差异特性的模糊空间Ωs&Ωt,如图1(b)所示,有条件地扩大匹配范围,将边缘待定位点归属于模糊空间,有效避免簇间相似度差异不显著的待定位点的区域误判现象。

(a) 硬聚类

3.2 双距离差异软聚类

3.2.1 双属性特征

利用指纹点间的欧式度量,定义聚类形成的簇间距离和簇内距离,以映射各参考点的类间稀疏性和类内紧密性。鉴于样本点的类间稀疏性与类内紧密性,可在一定程度上反应具有信号域和空间域之间非线性渐变特征的指纹点聚类的有效性[13]。笔者提出以聚类指纹点的双属性特征衡量其分类的鲁棒性,构建兼具参考点“类间-类内”双距离差异的软聚类方法,增加有限的定位计算开销,弥补严格切分时局部匹配算法误差大的缺陷。

不失一般性,平面空间内的参考点仅以其信号域均值为单一尺度进行初始聚类划分,生成T个簇Ω1,Ω2,…,ΩT,并记录其簇中心c1,c2,…,cT。考虑到簇边缘样本通常对簇内归属度较低,其区域判别更易受信号波动干扰,本文以此建立信号对空间判别影响的更新指标,解决过渡区样本点簇间相似性的误判问题。

(1) 类间稀疏度

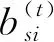
(1)

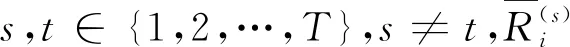
(2) 类内紧密度

(2)

3.2.2 软聚类生成

(3)

不难发现,f值越大,满足空间模糊的参考点越多,区域误判的概率则会越低。

双距离差异软聚类算法采用空间重叠分类结构解决基于RSS的指纹点目标区域归属问题,在通识的硬聚类算法构建指纹初划分的基础上,完成平面空间内所有参考点的双距离差异对比,判定模糊类属,进而实现整个目标环境由硬聚类向软聚类的转化。

3.3 双标签指纹库构建

平面空间模糊划分和类别重构过程,保证了每个参考点在离线指纹库构建中区域归属的稳健性。为提升在线定位的时效性,以类标签(或称区标签)和类内点标签的形式实现离线指纹库构建。

4 在线定位

4.1 区归属

4.2 点排序

考虑到待定位点与参考点位置越接近,则会在更多的接入点下接收到更加相似的信号强度值,将参考点和待定位点之间的RSS差异转化为相对排序,虽然可以削弱接入点的不确定因素对定位的影响,但信号动态特性所带来的排序误差依旧难以避免。基于此,本文不再局限地以点与点间欧氏距离衡量待定位点与指纹点间相似度,而是结合参考点近邻空间携带的定位信息量,弱化信号波动的影响,对参考点进行同源相似度的稳健排序,进而实现与待定位点间多源均衡相似度的有效判断。

4.2.1 同源相似度

(4)

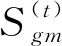
4.2.2 参考点同源排序

场景动态特性及其时间差异使得个别接入点在离线阶段和在线阶段特征缺乏一致性,甚至会出现绝对差的激增,从而导致待定位点与参考点邻近程度的误判。为了保证接入点之间比较的一致性,将同源相似度的量化比较转化为同源相似度的排序比较,以避免不同接入点间量级差异。参考点同源排序原理定义如下:

4.2.3 野值修正

信号自身波动和同源接入点下的其他参考点排序结果的交叉影响,可能导致部分参考点排序异常,鉴于低维空间域相近的参考点,通常在高维信号域具有更加相似的RSS值[14],因此,同源接入点下的近邻参考点应具有相近的排序。若某参考点与周围邻居点间的同源排序差异较大,该参考点排序为异常值的概率则更高。

在箱线图[15]过滤异常值方式的启发下,对同源邻居样本升序排序后进行四分位处理,记Qu和Qd为上、下4分位数,4分位距IQR=Qu-Qd,基于Qd和Qu缩放IQR的1.5倍进行有效区间的切分,构建关于归属区Ωt内参考点同源排序的野值修正模型:

(5)

4.2.4 参考点多源排序均衡

(6)

需说明的是,均一化后所得非整数排序结果,依然遵循排序规则。

4.3 点匹配

理想状态下,用于最终位置确定的Ωt个近邻点应该围绕待定位点[16],但由于环境的动态干扰和信号自身的波动,传统KNN、WKNN匹配算法所选择的Ωt个近邻点,并不能保证基于待定位点的集聚分布,且固定Ωt值会降低算法对环境的适应能力。为此,提出一种信号域和空间域迭代约束近邻点集合的定位方法,通过引入空间密度可达判别,搜索强相关参考点集,控制Ωt值自适应,提高近邻参考点选择准确性的同时保证其分布的相对集中。

4.3.1 强相关参考点集搜索

以点排序方法获取归属区Ωt中的所有参考点与待定位点的排序结果,取前I(I≤G)个参考点,生成初筛近邻集P′R={P′R1,P′R2,…,P′Ri,…,P′RI},考虑到信号域的不确定性,会伴随部分离群点的引入,如图2(a)所示,为克服野值点迭出对定位结果的不利影响,基于密度聚类[17]思想,利用初筛近邻点的空间域距离对目标近邻集进行二次约束。

(1) 以初筛近邻点P′Ri的空间坐标为中心,ε为半径,定义P′Ri邻域为

Eε(P′Ri)={P′Rj∈P′R|d(P′Ri,P′Rj)≤ε} ,

(7)

其中,d(P′Ri,P′Rj)表示集合P′R中两个初筛近邻点P′Ri和P′Rj之间的空间域距离,Eε(P′Ri)包含了P′R中与P′Ri空间域距离不大于ε的所有初筛近邻点。

(2) 设定领域阈值η以反映P′Ri周围近邻点密集程度,若|Eε(P′Ri)|≥η,则将P′Ri视为核心点(Core Point,CP)。若存在核心点序列{CP1,CP2,…,CPh,…,CPH}⊂P′R,2≤H≤I,则依据式(8),判断序列中相邻核心点的前置项是否在后置项的邻域内,并以标签lh标识:

(8)

形成的H-1个标签共同决定核心点序列{CP1,CP2,…,CPh,…,CPH}是否具备构成目标近邻集的可能性,定义

(9)

若L=1,则CPH距离CP1密度可达,表明该核心点序列空间域较为接近,其携带的指纹信息相似度较高,具备构成目标近邻集的可能性;否则,不具备构成条件。

(3) 以任意一个核心点CP作为起点,从该核心点密度可达的所有核心点构成一个簇;再从其余尚未成簇的核心点中寻找可成簇的新起点,以此完成强相关参考点候选集的搜索,如图2(b)所示,无法成簇的点则被视为弱相关参考点。显然,领域半径ε和领域阈值η联合约束了参考点候选集的相关程度。

4.3.2 目标近邻集匹配

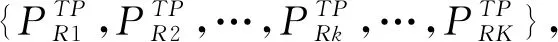
(a)初次约束:初筛近邻集

需提出的是,存在某待定位点的初筛近邻集全被判断为弱相关参考点这一特殊情况,此时则同样以初筛近邻集作为该待定位点位置估计的目标近邻集。

强相关参考点集搜索过程在剔除数据集弱相关参考点的同时,确保了目标近邻参考点集物理空间位置的集中分布,为待测点TP近邻点集合的自适应匹配创造了条件,以此克服了因加权质心的偏移而导致定位结果偏差大的问题。

4.4 位置计算

参考点的多源排序均衡结果,体现了参考点和待定位点接收信号相似度的级别,因此以其作为待定位点定位权重的配置基础,表征如下:

(10)

(11)

5 系统定位流程

文中所提DLFS定位算法的系统流程如图3所示。针对区边界待定位点归属左右偏移问题,本文基于“类间-类内”指纹信息差异建立“左右逢源”的空间模糊聚类机制;并以构建双标签指纹库的形式,通过类标签信息提升区归属判别效益,引入类内点标签信息支撑下的参考点排序野值修正以及目标近邻集迭代约束,以此克服环境和信号的不确定性,使得定位系统更具可靠性。

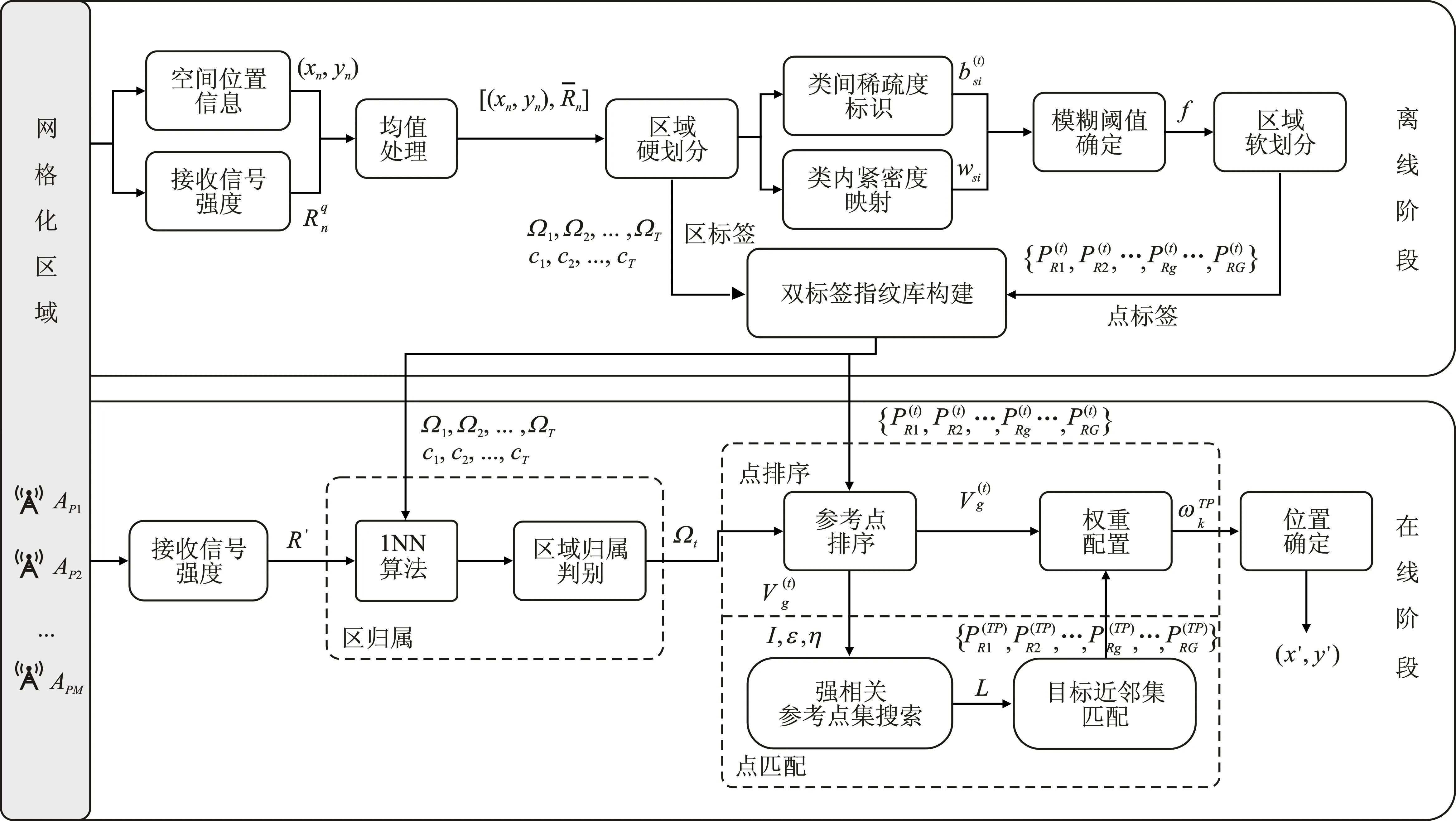
图3 DLFS定位算法流程图

6 实验场景与结果分析

6.1 测试场景与数据处理

为了评估DLFS 定位算法性能,以江南大学物联网工程学院3楼内,人员走动频繁的多边形连通走廊为实景测试场地,该场景可以较好地反映环境多变和信号动态特征对定位的影响,具有很强的实测代表性。

参考点采用均匀网格部署形式,相邻参考点间隔取1 m,共计N=270个参考点;在全局定位区域共探测到来自M=86个接入点的信号,为保证点与点间计算维度的一致,不失一般性,每个参考点处未探测到的接入点信号强度值以-100 dBm填充[18],并以2.3 s采样间隔,采集Q=60次指纹数据。沿着实验走廊中间区域选择152个在线测试点。为避免设备差异对算法性能评估的影响,离线与在线过程,均使用同一移动终端作为数据采集工具。所有数据均以Matlab 2020a作为处理平台。

6.2 参数配置对性能的影响

6.2.1 模糊阈值f

模糊阈值f影响着子区域匹配的包容度,f值越大,区域判别精度越高;与此同时,重叠区域的参考点数量将增多,计算代价随之增大。为兼顾区归属正确率和点匹配时效性,以随机选取离线采集中的60×80%=48次数据取均值作为训练数据,其余60×20%=12次为测试数据,重复10次试验,分别记录区判别正确率和参考点全局增长率的均值,以评估最佳f的配置影响。

实验对比了不同f值下区判别正确率和参考点全局增长率的变化情况,如图4所示。可以发现,即使f取值小量程增长,也可显著提升区判别正确率,且在f=11时,区判别正确率达到99.68%,同时参考点全局增长率仅为10.37%,主要原因在于双距离差异越小的参考点,越易引发误判,小范围的误差容忍,即可换取系统定位精度的快速上升。此时,若持续扩大f值,区判别精度上升缓慢,参考点的计算量呈现明显增长。因此,本实验场景设置模糊阈值f=11。

图4 模糊阈值f对性能的影响

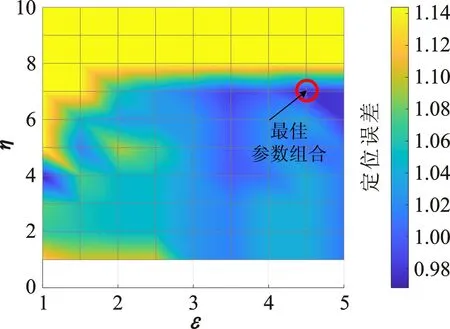
6.2.2 领域参数ε和η

为使系统的定位性能达到最佳,对4.3.1节中的相关参数进行寻优。基于固定近邻点取值的经验范围,综合考虑强相关参考点集搜索的可行性和计算负担,折中选取归属子区域中参考点总量的20%作为初筛近邻点的数量,即I=G×20%。为评估定位区域中领域半径ε∈{1,1.5,2,…,4.5,5}和领域阈值η∈{1,2,…,10}的多重配置方案对定位性能的影响,同6.2.1节中模糊阈值寻优方法一致,以确定各子区域的平均定位误差最小时的领域参数组合,从而保障待定位点自适应匹配的定位效果。限于篇幅,图5给出了部分子区域在不同领域参数组合下的定位性能。

(a) 子区域Ω2

实验发现,不同的领域参数组合(ε,η),伴随着子区域不同的定位性能。此外,表1列出了上述子区域在其最优参数组合下,对应子区域内部分待定位点TP在位置计算时的近邻数K,其匹配差异进一步证明了不同待定位点在定位时目标近邻集会随着定位需求发生自适应的改变。

表1 部分子区域内最优领域参数

6.3 区域软聚类效果分析

考虑到聚类算法的时效性,论文选用常规k-means作为区域初划分算法,结合环境特性和k-means聚类效益,本实验场景预设初始聚类数为7。基于模糊聚类机制,配置最佳模糊阈值f=11,形成7个独立区和6个模糊区,聚类效果如图6所示。

图6 区域软聚类结果示意图

所提算法的软标记性质体现在双距离差异较小的28个参考点的重叠划分上。实验发现,具有模糊划分属性的参考点,基本都位于子区域的边界处。这些参考点双区域的归属结果进一步印证了过渡区信号稳健性的不足,由于空间结构变化和信号交叠等干扰,使得边界地带更易引发区域误判的问题。显然,模糊空间的设置,可弱化区域信号不稳定的影响,控制区域定位误差。

相较于全局式贪婪匹配,本文所提软聚类方法将整个目标区域内的N=270个参考点降低至局部区域内的24～53个参考点,很大程度上保障了定位的实时性;此外,28个参考点的重叠划分,分配至各子区域仅相对新增1～7个有限的参考点,对比严格的硬划分算法所增加的局部匹配工作量也是相对可控的。

6.4 在线算法结果分析

针对传统排序算法对信号动态特性考虑欠缺的问题,本文利用参考点近邻空间整体信号特征对排序野值进行修正;同时为克服传统匹配算法K值固定的缺陷,论文基于对参考点信号域和空间域的迭代约束实现K值自适应。为有效评估其对在线定位的价值,论文通过控制算法执行,从“传统参考点排序+固定K值”“仅执行K值自适应”“仅执行参考点排序修正”“参考点排序修正+K值自适应”4个角度对定位性能进行了对比实验,结果如表2所示。

表2 在线算法对定位误差的影响

从实验数据发现,在参考点排序修正和K值自适应的共同作用下,定位效果最佳,平均定位误差为 1.138 m,相较于传统定位的1.327 m提高了18.9%,1 m以内误差占比提升了9.46%;在线定位中,仅进行参考点排序修正和仅采用K值自适应平均定位误差分别降低了0.126 m和0.061 m。结果验证了所提“点排序”和“点匹配”在线算法对定位的可行性和有效性。

6.5 整体定位性能分析

为验证本文算法DLFS的整体定位性能,分别与6种同类算法进行比较。其中,传统的WKNN[7]、EWKNN[11]、AAS[10]为3种全局匹配算法;此外,补充3种不同离线区域划分算法,即APC[6]、FCM[5]、k-means[4],同文中在线方法结合。为了保证对比的公平性,各算法均已选取本实验场景下的最佳参数进行实验。

表3总结了不同算法定位性能。实验结果表明,相较其他方法,本文算法的平均误差、最小误差以及方差误差都是最低的。整体定位场景中,其平均定位误差为1.138 m,在局部匹配方法中改进了4.7%～11.8%,但最大误差相差不大;与全局匹配算法相比,本文算法的平均定位误差至少降低了14.7%。表明本文算法为复杂室内环境下的定位性能带来了整体性的提升。

表3 7种定位算法性能比较 m

图7给出了包含全局匹配和局部匹配在内的共计7种算法的定位误差累计概率分布,在对待定位点位置估计时,同等精度范围内,本文所提DLFS算法均优于其他对比算法。DLFS算法在同全局匹配的比较中,有73.78%的估计精度在1.4 m以内,相较于此时的WKNN算法,估计精度提升了21.35%,如图7(a)所示。由图7(b)可知,随着定位误差范围的扩大,4种局部匹配方法的误差累计概率上升状态趋于一致,当定位误差范围扩大至0.4 m后,DLFS算法呈现优势,并在其扩大至2.4 m时,累计误差概率达到90.00%。实验证明,DLFS 在解决环境和信号动态特性带来的定位问题时具有显著的优势,主要得益于该模糊聚类机制在处理边界信号跳跃问题的敏感性,以及在线定位方法对指纹点与待定位点间相似度的高效衡量。

(a) 与全局匹配算法的比较

7 结束语

针对定位中,匹配效率与定位精度的需求,算法在平衡区域匹配精度与定位计算代价后,构建了待定位场景下的模糊聚类机制。综合考虑每个参考点的类间稀疏度与类内密集度,实现相邻区域的簇间边界调整;借助邻居指纹信息弥补各参考点波动差异后,采用空间域和信号域迭代约束方案选取各待定位点的最佳邻近点集合,从而降低定位误差。实验证明,本系统模型有效衡量了待定位点与参考点的空间距离,更好地克服了信号和环境的动态影响,在计算量大大减少的同时,在复杂的室内环境中定位效益也较高。