水平管内黏稠油水环输送的稳定性

尹晓云，苏 明，周 鑫，张 良，敬加强

1.中国石油西南油气田分公司安全环保与技术监督研究院，四川 成都 610041；2.页岩气评价与开采四川省重点实验室，四川 成都 610041；3.国家管网集团西南管道有限责任公司建设项目管理中心，四川 成都 610094；4.西南石油大学石油与天然气工程学院，四川 成都 610500；5.油气消防四川省重点实验室，四川 成都611731

引言

随着轻质原油的逐渐枯竭，人们对稠油的需求日益增长，但稠油黏度高、密度大以及流动性差等特点给开采与储运带来极大困难与挑战[1]。针对稠油的管道输送问题，目前多采用加热、稀释、加剂等降黏减阻方法，但普遍存在处理量大、能耗高及外加介质多等问题，而水环等低黏介质润滑因减阻效果显著、用量少及管壁污染小等优势而备受世界石油界的广泛关注与重视。

目前，国内外专家学者对水环输送稠油技术的研究主要集中在以下5 个方面：1）水环发生器的优化设计[2-5]；2）水润滑减阻实验及减阻效果评价[6-8]；3）油-水两相流的流型特征及压降规律[9-10]；4）油-水环状流压降与持液率预测模型的建立[11-13]；5）水环输送管道的停输再启动[14-17]。涉及水环结构动态稳定性的研究则相当少[18-19]，但要实现水环输送技术的工业化推广应用，必须解决水环边界层的稳定性问题，这样才能确保油-水环状流在长时间、长距离的现场管输中仍能保持相对稳定的流动状态。

本文采用数值模拟方法探究水平管中流体性质（油-水密度差、油-水黏度比、油-水界面张力）对油-水环状流结构稳定性的影响，通过对比分析不同工况下的油水两相分布特征（体积分数分布云图、截面平均含油率）和水环稳定性评价指标（油芯偏心率、水环维稳长度比、管输压降），确定模拟条件下水环输送稠油的最佳工况范围，为增强油-水环状流的稳定性提供理论参考。

1 模型建立

1.1 计算模型

1.1.1 控制方程

在计算流体力学（Computational Fluid Dynamics，CFD）领域，基于流体体积（Volume of Fluid，VOF）[20]的数值方法最适合研究两相不相溶的分层或环状流流型，且能实现对两相运动界面的追踪，捕捉不断演化的流动结构。在本研究中，稠油和水是两种互不相溶的液体，且以环状流的形态在管道中流动。此外，采用两相界面的位置分布和掺混情况作为评价水环稳定性的关键参数。因此，选用VOF 多相流模型实现对稠油-水环三维管流的数值模拟研究，其基本方程为[21-23]

为描述油-水的界面张力，采用Brackbill 等[24]提出的连续表面张力（Continuum Surface Force，CSF）模型，其表达式如式（6）∼式（9）所示。在该模型中，求解器会把表面张力视作外部体积力，并将其以源项的形式合并在动量方程式（2）中。

式中：σow—油-水界面张力，N/m；

Fσ— 油-水界面张力系数，无因次；

κ—界面曲率，m−1；

n—曲面法线，定义为油相体积分数的梯度，无因次；

n—单位法向，无因次。

1.1.2 湍流模型

考虑油-水两相黏度及两相在管内流动时的操作条件，可发现整个模拟范围内油相与水相分别保持层流状态和湍流状态。由于标准k−ε 模型具有适用范围广、精度合理及经济性好等优势，广泛应用于工程流场计算[25-27]。因此，选用标准k-ε 模型描述湍流流动过程，其输运方程为[28-29]

1.2 物理模型

1.2.1 几何模型

建立如图1 所示的三维几何模型，管道水平布置，其内径D1为25 mm，长度Lt为1 m（40D1），油相入口内径D2为21 mm，环空间隙e为2 mm。油相与水相分别从管道中心与油壁间的环空注入后沿Y轴正方向同向流动，二者在流动过程中均会受重力（Z轴负方向）影响。

图1 油-水管流模拟几何模型Fig.1 Geometric model of simulation of oil-water pipe flow

1.2.2 网格划分及无关性验证

采用ANSYS Workbench 中的Mesh 模块对管道模型进行多域扫描网格划分，为了减少体积单元数量，提高解的收敛速度，计算区域内全部采用六面体网格。同时为了准确捕捉靠近壁面处的流动情况，对靠近管道进出口及管道壁面处的网格进行加密设置，管道模型的网格划分结果如图2 所示。

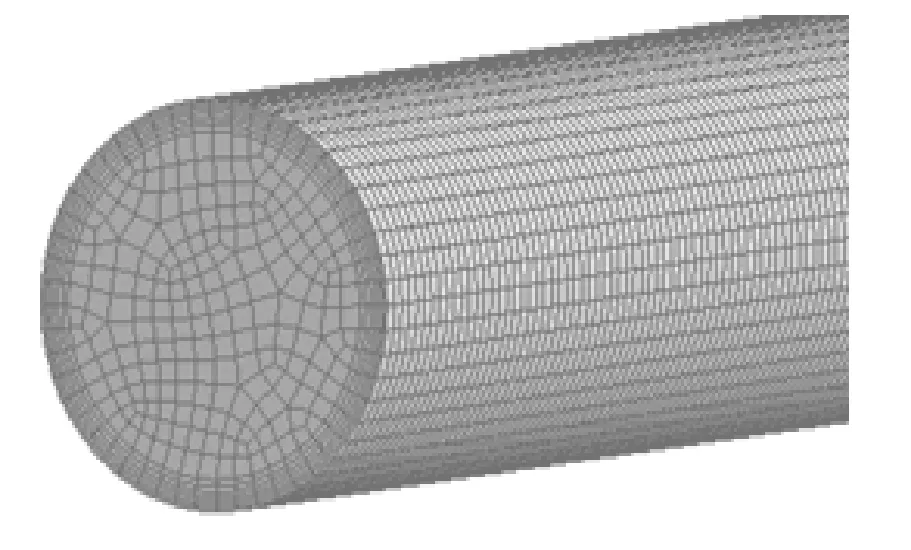
图2 管道模型网格划分Fig.2 Partial grid of pipe geometry

为验证模拟管段的网格无关性，将其划分为4 套数量不同的网格，网格数量分别为335 265、456 476、542 921 和623 922。由图3 可知，网格数量从335 265 增至623 922 时，管流压降与油芯偏心率（Y=0.75 m 截面）的变化都很小。因此，为保证计算精度较高、耗时较少的同时尽可能获得清晰的油水界面，最终选定网格数量为542 921 的模型进行后续模拟计算。

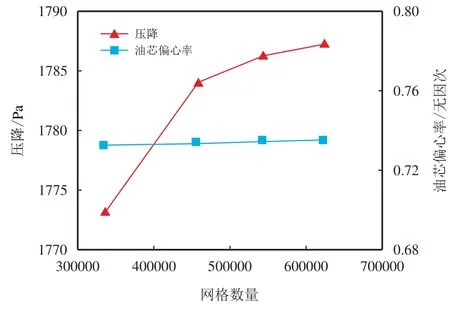
图3 网格无关性验证Fig.3 Verification of grid independence

1.2.3 边界、初始条件

油相与水相入口选定为速度入口，油相流速为0.5 m/s，水相流速为0.5 m/s；两相出口选定为压力出口，出口压力设置为0.1 MPa；壁面选定无滑移边界条件。与实验时的初始条件保持一致，设定油-水两相注入前模拟管内充满水相。

1.2.4 物性参数

基于油-水两相管流实验中所使用稠油和自来水的物性参数（20◦C），初始模拟中油相密度与黏度分别为926.4 kg/m3和1 143.3 mPa·s；水相密度与黏度分别为998.2 kg/m3和1.0 mPa·s；油水界面张力为32.36 mN/m。

1.2.5 离散方法及收敛准则

采用FLUENT 15.0 对油-水两相水平管流进行步长为10−3s 的瞬态模拟，将水设置为主相，油设置为次相。压力速度耦合采用PISO 算法，连续性方程采用PRESTO 模式离散，动量方程和湍流方程均采用二阶迎风差分模式离散。当输运方程中不同变量的残差低于10−4且进出口管道质量流量相等时即认为数值计算已达到收敛。

1.3 模型验证

为验证数学模型及计算方法的可靠性，自主设计加工并搭建了水环输送稠油减阻模拟管路系统[30]，对比分析不同流速组合（Uo=0.5 m/s，Uw=0.1∼0.5 m/s），两相管流流型特征（图4）和压降特性（图5）的实验结果与模拟结果。由图4 可见，数值模拟结果中油水界面清晰，油相分布于管道中心，水相不均匀地分布在管壁周围，重现了环道实验中观察到的上薄下厚水环包裹核心油流的偏心环状流形态；由图5 可知，实测压降值与数值模拟压降值非常接近（最大相对误差10.2%），且变化规律及趋势一致。这表明本文采用的计算模型与计算方法具有较高的可靠性，能够准确捕捉水环的流型特征及水力特性，可以实现油-水环状流在水平管中的流动模拟。

图4 拍摄流型与油水分布云图对比图Fig.4 Comparison of photographs of flow regimes and cloud charts of oil-water distribution

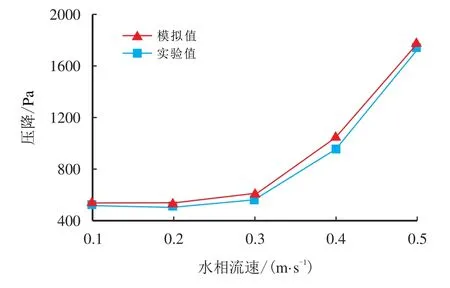
图5 实测压降值与数值模拟压降值对比图Fig.5 Comparison of experimental data and numerical simulation

1.4 评价方法

1.4.1 截面平均含油率

为充分反映管道中油相分布特征及其变化规律，引入截面平均含油率

蒋大伟把车开到兰江大桥下，抬头向桥面上看去，郑馨也向桥面看去。眼前的兰江大桥宽阔伟岸，桥面上车辆川流不息。蒋大伟轻轻吸了一口气：终于到了，多美的兰江大桥！郑馨脸色阴沉，看着桥头，没有说话。蒋大伟感叹地：人要是站在桥上，就像一片树叶。郑馨还是没有说话，她打开车门。蒋大伟说：等等！你改变主意没有？现在还来得及！郑馨也叹了一口气：不，我不会改变主意的。蒋大伟说：人的生命只有一次，跨过这道门槛，就再也回不来了！郑馨回道：既然跨过门槛，就不想再回来了，我想永远睡在这里，看日出云飞，潮落潮涨，没有苦闷，没有烦恼。蒋大伟摇摇头。

1.4.2 油芯偏心率

由于核心油流与水环的性质不同，核心油流会上浮或下沉而偏离管道中心，使最初的同心液环流动转变成偏心液环流动（图6），从而影响油水核心环状流的稳定性。因此，引入油芯偏心率E来评价水环结构的稳定性[31]，其计算式为

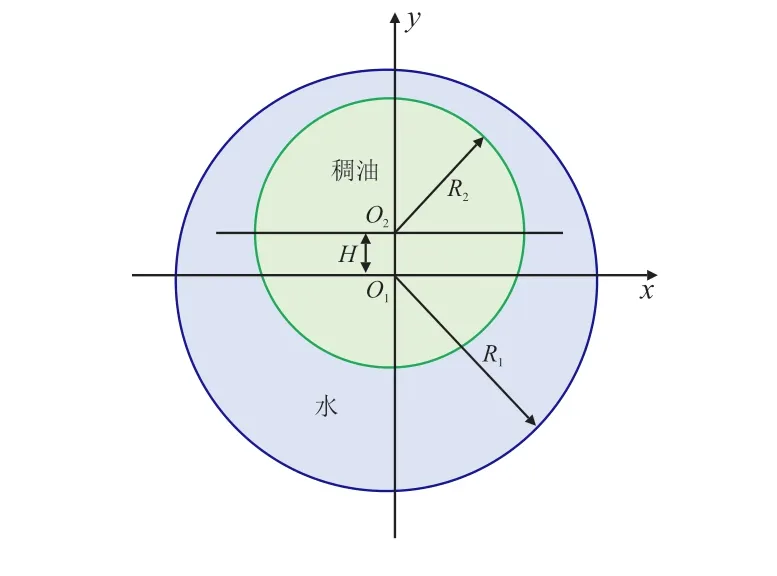
图6 偏心水环输送示意图Fig.6 Schematic diagram of eccentric water annulus transportation

1.4.3 维稳长度比

为探究油-水两相形成环状流后能够保持连续稳定流动的距离，定义油-水稳定流动的长度比l（r图7），其计算式如式（16）所示。式中的维稳长度Lt指水环包裹着油流向前流动的距离，在该流动过程中水环将黏油与管壁完全隔离，黏油不会接触管壁而黏附于管壁上。本文基于观察中截面和管道不同位置横截面上的油水两相体积分数分布云图，并辅以管道沿线压力梯度的变化情况（相较于失稳点前较低且恒定的压力梯度，失稳点后的压力梯度会增大）来判定维稳长度。

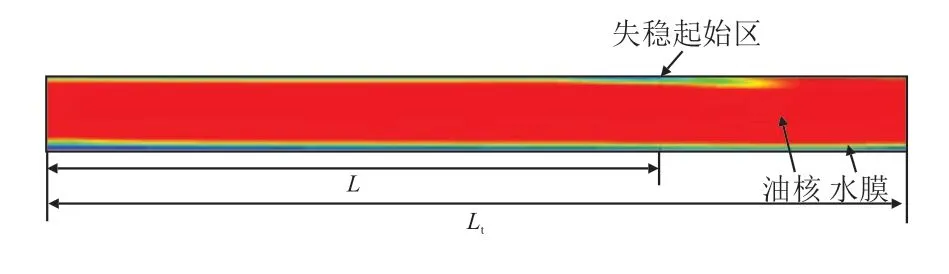
图7 水环维稳长度示意图Fig.7 Schematic diagram of stable length of water annulus

2 结果与讨论

2.1 油-水密度差对水环稳定性的影响

不同油相密度（ρo=926.4∼996.4 kg/m3，间隔10.0 kg/m3）下，沿管流方向Y=0.75 m 位置处管道横截面上的油水两相体积分数分布如图8 所示。

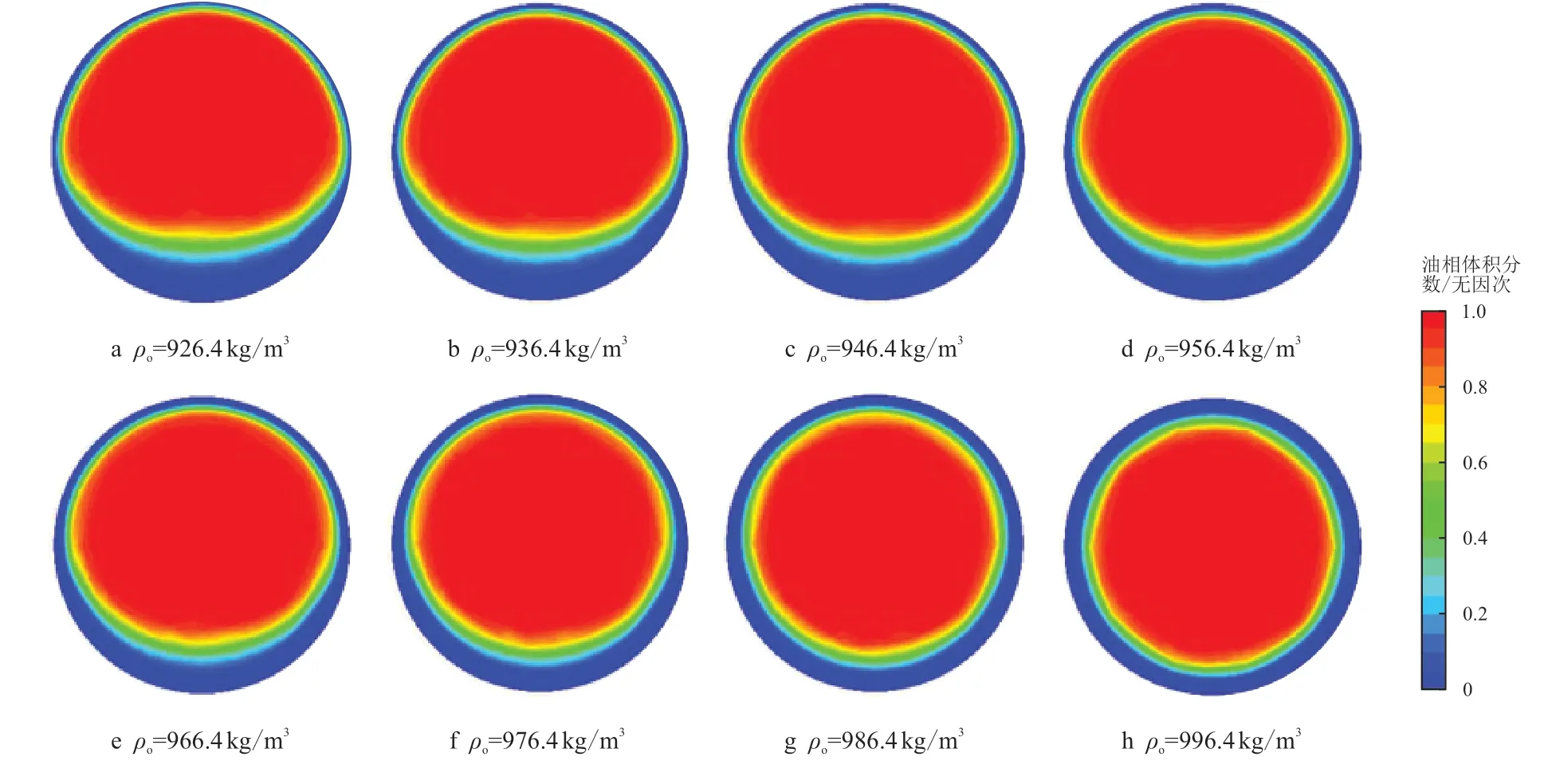
图8 不同油相密度下管道横截面上的油水两相体积分数分布（Y=0.75 m）Fig.8 Oil-water two-phase volume fraction distributions of different heavy oil densities in pipe cross-sections（Y=0.75 m）

由图8 可知，随着油相密度的增大（油-水密度差减小），核心油流的偏心程度降低，油水环状流动结构由偏心逐渐转变为同心，水环的稳定性逐步增强。

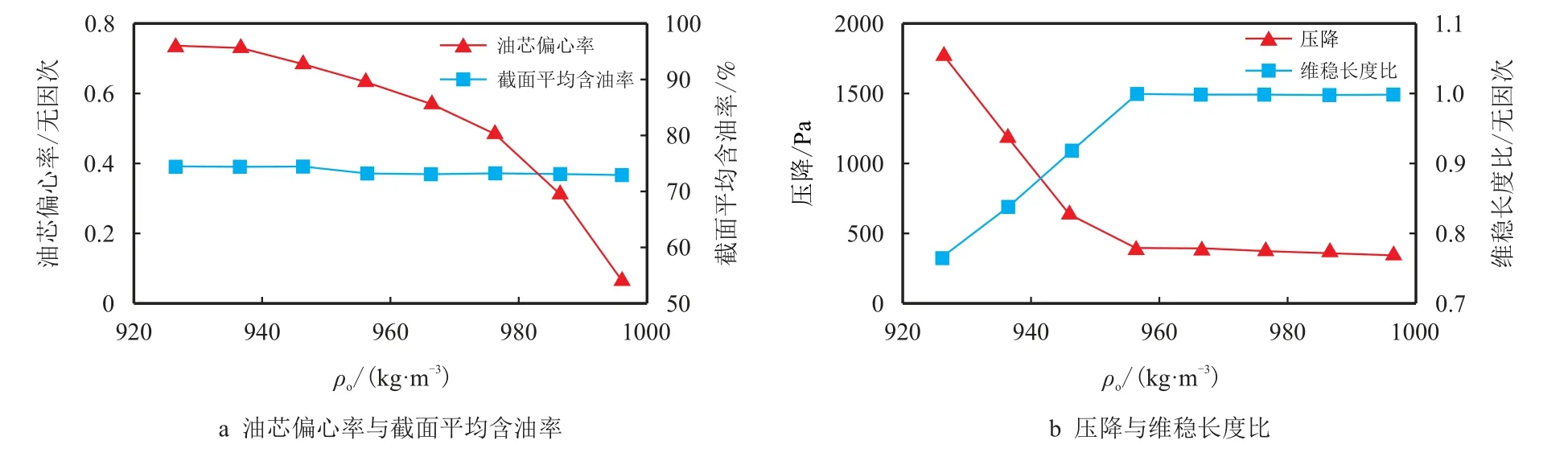
图9 水环稳定性评价指标随油相密度的变化曲线布Fig.9 Variation curve of water annulus stability evaluation indexes with heavy oil densities

2.2 油-水黏度比对水环稳定性的影响

图10 为不同油相黏度（µo=743.3∼1743.3 mPa·s，间隔200 mPa·s）下沿管流方向Y=0.75 m 位置处管道横截面上的油水两相体积分数分布图，图11 为油相黏度对截面平均含油率与水环稳定性评价指标的影响。

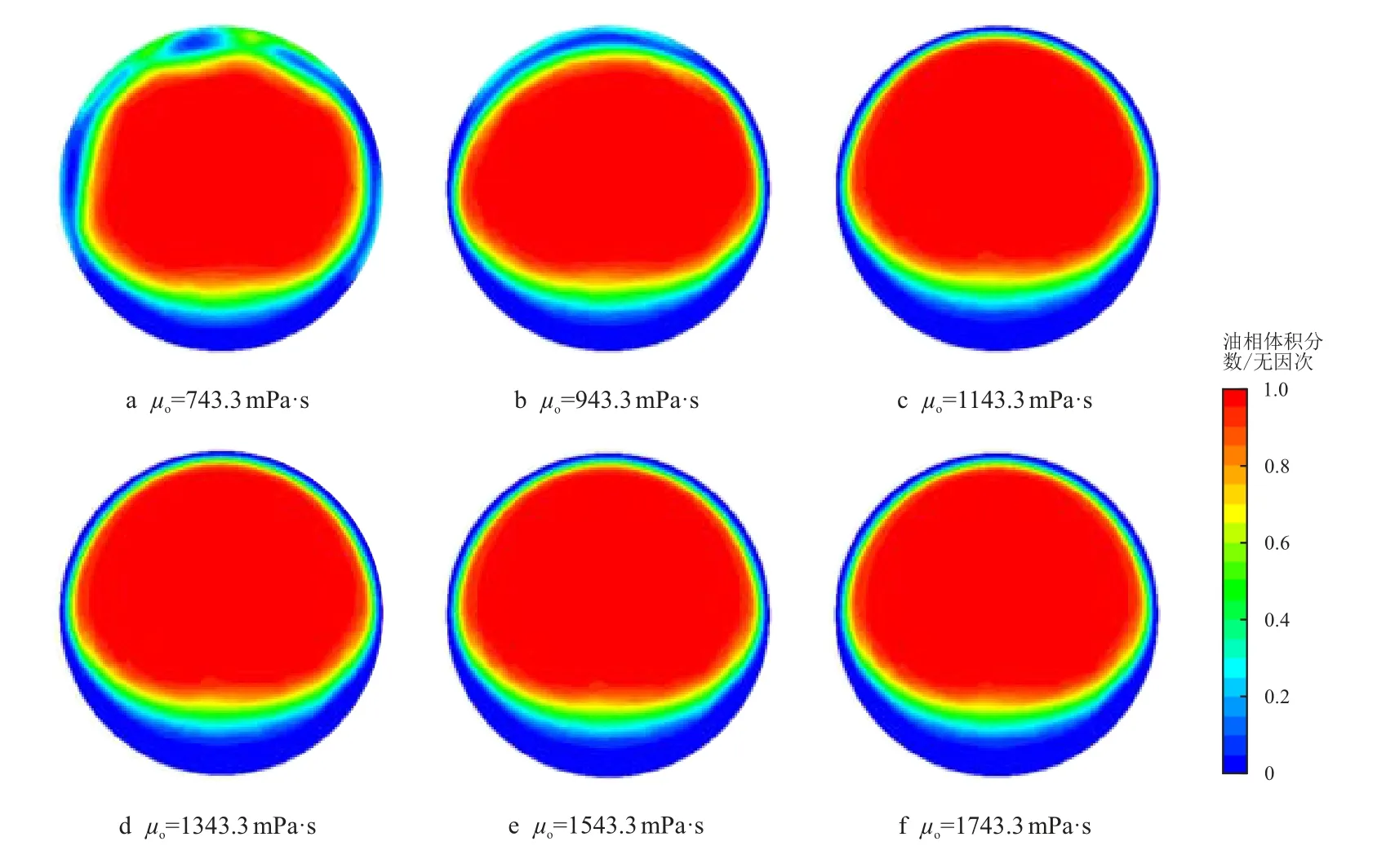
图10 不同油相黏度下管道横截面上的油水两相体积分数分布（Y=0.75 m）Fig.10 Oil-water two-phase volume fraction distributions of different heavy oil viscosities in pipe cross-sections（Y=0.75 m）

从图10 和图11a 中油芯偏心率随油相黏度变化关系可知，当油相黏度小于943.3 mPa·s 时，核心油流上浮偏心严重（E=1.00），油水两相在交界面处剧烈掺混，致使水环失稳破坏，水环不再包裹核心油流向前流动，油流与管壁相接触；当油相黏度大于943.3 mPa·s 时，核心油流上浮偏心程度降低（E=0.73），位于管道上部的水层受到油流的挤压作用虽会变薄但不至失稳破坏，油流继续以被水环包裹着位于管道上部的形态向管道出口流动。

由图11a 中截面平均含油率随油相黏度变化曲线可知，在选用的油相黏度范围内，截面平均含油率随油相黏度的变化很小，不同油相黏度下截面平均含油率都约为73%。

从图11b 可以看出，随油相黏度增大，压降呈单调下降趋势；而维稳长度比随油相黏度的变化规律与压降的变化规律正好相反，即呈单调上升趋势。这是因为流体在管道内的流型主要取决于重力与黏性力之比，当比值较小时，即黏性力占主导地位，油-水两相流动易形成环状流结构；反之，则易形成分层流结构。当油相黏度增大时，流体重力与黏性力之比减小，因而，管内流型由主要受重力主导转变为受黏性力主导，环状流动的稳定性增强，从而使保持环状流动形态的距离增长，管流阻力降低，减阻效果变好。

2.3 油-水界面张力对水环稳定性的影响

不同油水界面张力（σow=22.36∼52.36 mN/m，间隔10.00 mN/m）下沿管流方向Y=0.75 m 位置处管道横截面上的油水两相体积分数分布见图12。

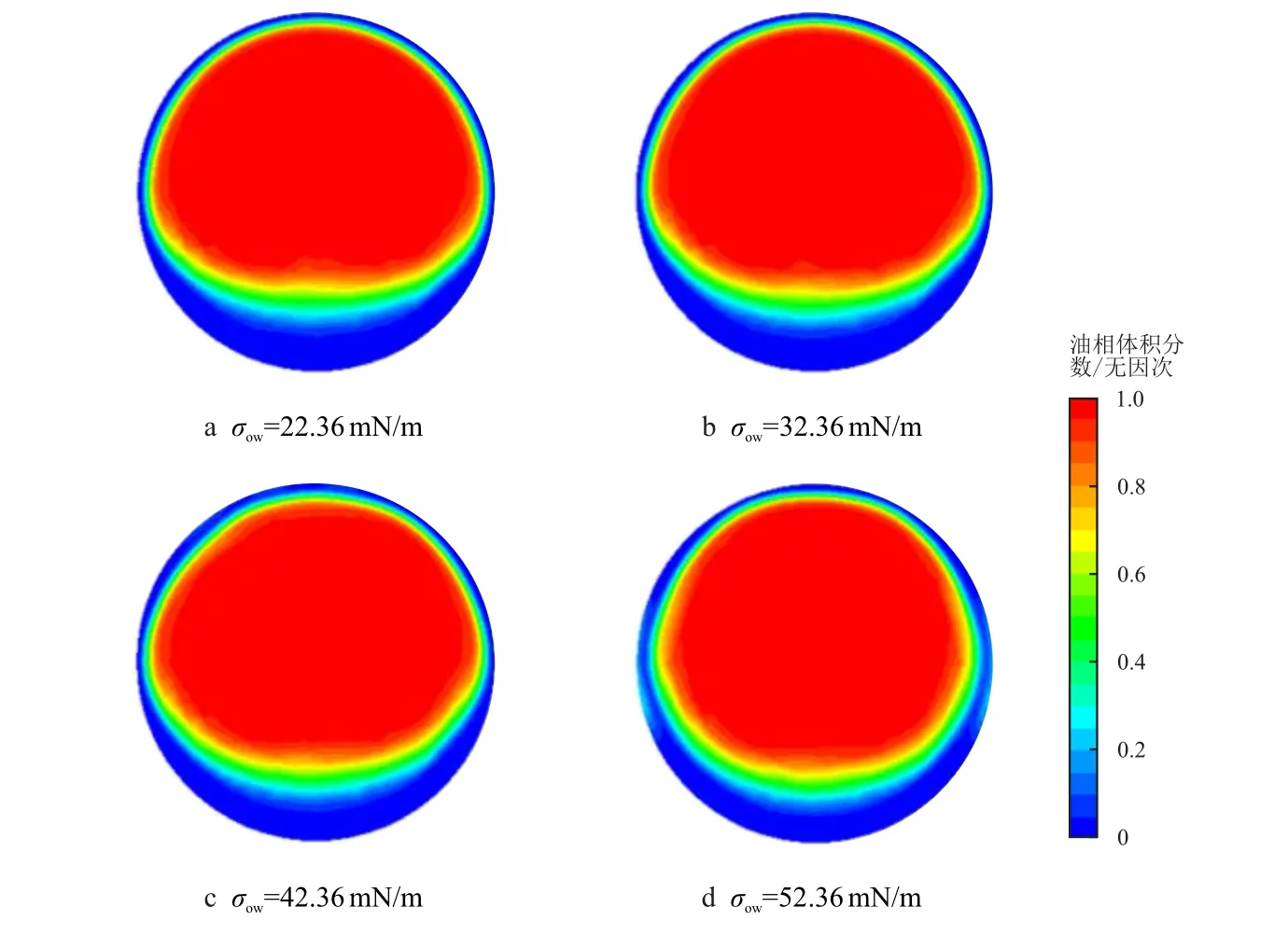
图12 不同油水界面张力下管道横截面上的油水两相体积分数分布（Y=0.75 m）Fig.12 Oil-water two-phase volume fraction distributions of different interfacial tensions in pipe cross-sections（Y=0.75 m）

从图12 可知，当σow由22.36 mN/m 增加到32.36 mN/m 时，核心油流向管道上部偏移的距离减小；当σow=42.36 mN/m 时，核心油流向管道上部偏移的距离进一步减小，但油芯变形程度增加，相较之前变得更扁平；当σow=52.36 mN/m 时，核心油流向管道上部偏移距离增大的同时油芯变形程度增大，致使油流与管壁左右两侧相接触。

截面平均含油率与水环稳定性评价指标随油水界面张力的变化规律见图13。如图13a 所示，截面平均含油率随油水界面张力的变化规律与其随油相密度和黏度的变化规律基本一致，即截面平均含油率几乎不随油水界面张力的变化而变化，不同油水界面张力下截面平均含油率均约为73%。核心油流的偏心程度随油水界面张力的增加呈先减小后增大趋势，这是由于界面张力的增加会使竖直方向上朝下的润滑力增大，而作用在核心油流上的浮力却不变，因此，相较于界面张力较小时润滑力较小的情况，油流在上浮过程中只需移动更短的距离就能达到平衡[12，26]。但当界面张力增大到一定程度时，油芯的变形会使交界面处油水两相的掺混、扰动加剧，从而导致油流在上浮过程中达到平衡位置时的偏移量增大。由图13b 可看出，压降随油水界面张力的增大呈单调上升趋势；与此相反，维稳长度比随油水界面张力的增大呈缓慢下降趋势。主要是因为油水界面张力的增加虽能降低油芯偏心程度，但降低程度不明显，且同时会增大油芯变形程度，使油芯与管壁左右两侧相接触，继而导致环状流失去相对稳定的流动形态，流动阻力增大，减阻效果变差。

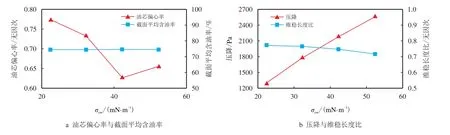
图13 水环稳定性评价指标随油水界面张力的变化曲线Fig.13 Variation curve of water annulus stability evaluation indexes with oil-water interfacial tensions

3 结论

1）油-水密度差、油-水黏度比及油-水界面张力对油水两相体积分数分布规律有较大影响，尤其是油相位于管道中的位置和水相在管道上部与下部的分布特点，在本文所采用的工况下油-水环状流总体上呈上薄下厚的水层包裹位于管道上部的核心油流的偏心结构；而其对截面平均含油率基本没有影响，在不同模拟工况下截面平均含油率均约为73%。

2）油-水密度差和油-水黏度比对水平管中水环的稳定性影响较大，水环的稳定性随油-水密度差的减小和油-水黏度比的增大而增强。因此，在实际输送过程中，为保证较低的偏心程度、较小的流动阻力和较长的输送距离，应尽可能减小油-水密度差，增大油-水黏度比。在模拟条件下当油相密度为996.4 kg/m3，油相黏度为1 743.3 mPa·s 时，水环的稳定性最好。

3）油-水界面张力较小时，水平管中水环的维稳距离较长，输送压降较小，但此时油芯偏心率较大。因此，在现场输送过程中，应综合考虑各个稳定性评价指标的影响。由于一般情况下采用水环输送稠油时主要关心维稳距离和管输能耗，故在讨论条件下当油-水界面张力为22.36 mN/m 时，水环的稳定性最好。