考虑连接间隙磨损的水中浮体功能可靠性研究
2023-05-10何孔德方子帆杨蔚华刘绍鹏
何孔德,胡 昊,方子帆,杨蔚华,刘绍鹏
1.水电机械设备设计与维护湖北省重点实验室(三峡大学),湖北 宜昌443002 2.三峡大学机械与动力学院,湖北 宜昌443002
引言
随着海洋系泊技术的发展,缆系式水中浮体的应用越来越广泛,研究的学者也越来越多,但是当前学者对这些结构的研究大多是分类进行,研究了不同结构独有的特性,从宏观上研究了整体结构性能。但是由于这类结构工作于一定工况的水域,受到随机波流的联合作用,外界随机变化的波流除了对这类结构整体动态特性有一定影响外,对缆索和结构体的连接部位也会产生很大的影响。连接部位由于有运动的需要,在装配时会有一定的间隙,在长期的运动过程中,连接部位不可避免地会产生磨损,连接部位的磨损又会对整个结构的动态性能产生影响,因此,本文针对这类模型,考虑连接间隙磨损的影响所引起的连接部位接触状态的变化,以此来研究模型整体的动态性能及功能可靠性。
缆系式水中浮体结构在随机波流联合作用下会产生横摇、纵摇、艏摇以及横荡、纵荡、垂荡运动。本文主要针对位于顺流速方向的水中浮体,开展考虑连接间隙磨损情况下纵荡位移和纵摇角度可靠性的研究。设备可靠性的研究主要围绕结构强度可靠性以及机构功能可靠性。Kabir 等[1]采用自下而上的研究方法,分别研究每个零件的失效对产品性能的影响,从而获得影响产品整体性能失效的主要模式,这种以定性分析为主的研究方法,主要用于机械产品、电子产品的失效模型研究。孙利娜等[2]采用退化数据的方法来研究机械结构的可靠性,优点是可以准确预测简单结构的可靠性,但是不能考虑结构的损伤对整体可靠性的影响及灵敏度计算。Mohammad 等[3]在研究飞机起落架机构的可靠性时,同时考虑了结构件的受力变形和连接处的磨损,研究了系统的位置精度可靠性及结构可靠性,使Monte Carlo 方法在可靠性的计算中得到发展。谭兴强等[4-5]通过小子样、随机性理论研究了考虑磨损因素的四杆机构运动输出精度及可靠性问题。针对缆系式水中浮体的研究主要集中在风电浮式基础、海洋平台及波浪发电装置等。Liu 等[6]针对风电浮式基础,应用哈密顿原理,建立了风机塔架和叶片的耦合动力学方程,进行了相关动力学分析,揭示了外界不同载荷作用下风机塔架的振动频率分布规律。谷家扬等[7]针对风电装置进行了气弹响应分析,把风机塔架和叶片考虑为柔性结构,采用马休方程,研究了整体机组在风浪联合作用下的稳定性。Chen 等[8]研究了海洋平台在随机非线性波浪作用下碎波与平台基础的耦合响应,解决了碎波与结构物的耦合数值计算问题。Esteban 等[9]利用模型预测方法,分析了风机叶片的极值载荷,并采用动力学灵敏度计算方法,研究了结构参数变化对动力学特性的影响规律。Li 等[10]采用经典的莫里森理论建立了考虑流固耦合作用的海洋平台动力学模型,进行了时域分析和涡激振动分析,结果表明,采用考虑湿边界表面的耦合计算结果更接近工程实际。考虑连接部位的磨损影响来研究水中浮体动态特性的文献还很少;考虑单个部件受力、连接方式、局部磨损及破坏等因素对整体性能的影响、功能可靠性评判的文献也很少见。因此,本文在借鉴上述研究成果的基础上,开展考虑连接间隙磨损的缆系式水中浮体功能可靠性研究,进行功能函数的定义、评价,进而评判其主要功能的可靠度。
1 多体结构模型的构建
本文以某型缆系式水中浮体为研究对象,组成示意图如图1 所示,这种装置主要安装于一定深度的水下,主要由浮体、连接件、升降机构、声呐与传感器、系泊缆及锚组成。浮体作为安装平台,可以在上面安装监测装置及其他探测设备,对通过它上面水域的船只或其他设备进行监测,为了获取稳定可靠的监测信号,就要求这种装置本身具有一定的稳定可靠性,考虑到流速方向及结构对称性,可以把它简化为如图2 所示。图3 为连接件-浮体放大图、图4 为连接件-接头间隙局部放大图。

图1 缆系式水中浮体组成示意图Fig.1 Schematic diagram of cable-typed floating body
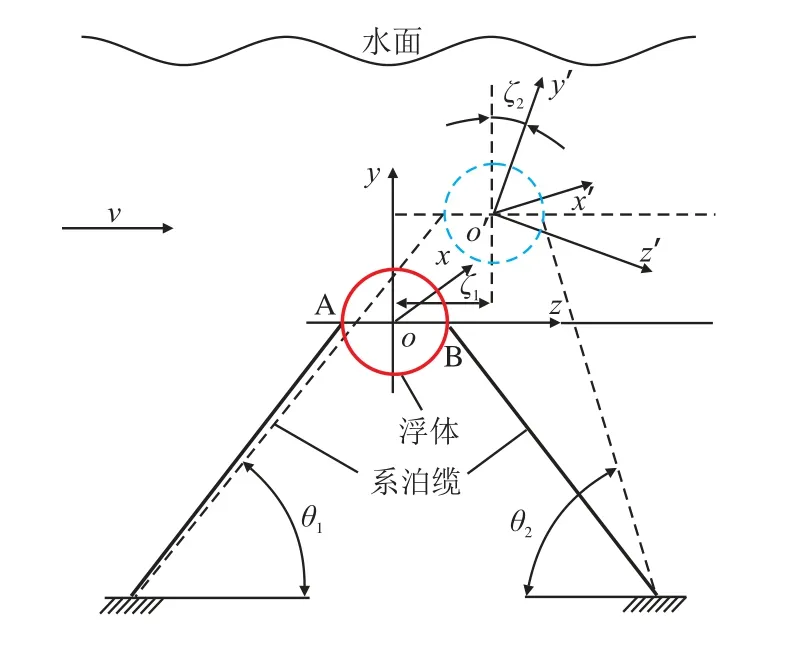
图2 简化示意图Fig.2 Simplified schematic
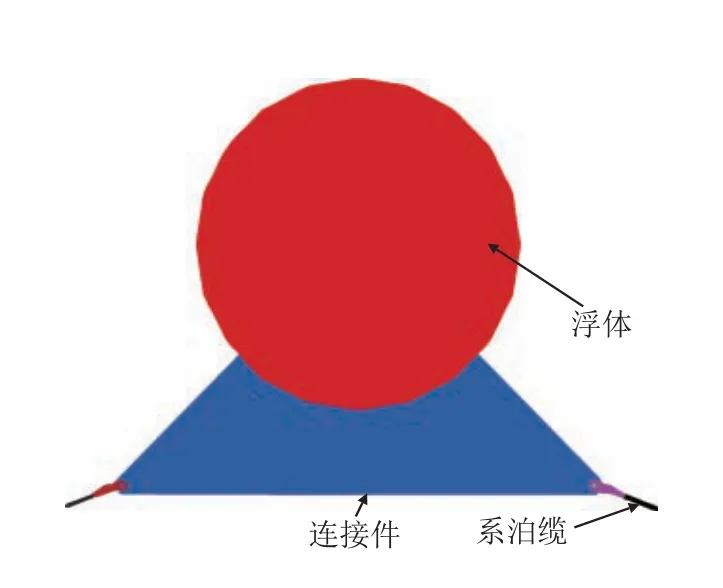
图3 连接件-浮体放大图Fig.3 Enlargement drawing of connection-floating body
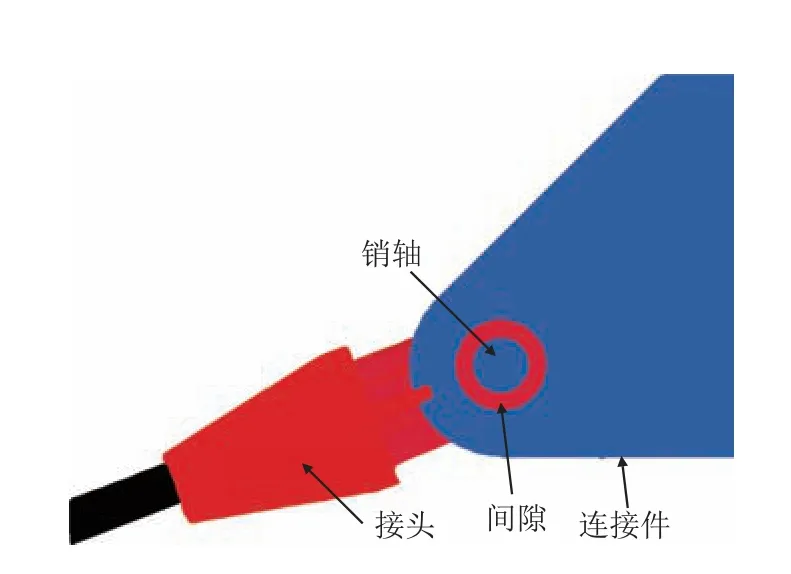
图4 连接件-接头间隙放大图Fig.4 Enlargement drawing of connection-joint clearance
2 耦合运动方程
处于流场中的浮体主要受到系泊缆约束力和流场作用力,其大小和方向与浮体形状、流场流速、方向以及浮体所处水深有关[11]。根据流体动力学理论[12],绕流阻力可以分解为平行于浮体轴线方向和垂直于浮体轴线方向,平行于浮体轴线方向的流场绕流阻力最小,垂直于浮体轴线方向的绕流阻力最大。根据图2,取浮体长度方向形心o为平衡位置坐标原点,与浮体轴线平行的方向为x轴方向,流场流速方向为z轴正方向,垂直于浮体轴线指向水面为y 轴正方向,建立坐标系。分析模型绕x轴的纵摇转动角度和沿z方向的纵荡位移的变化情况。浮体在受到流场作用力时会偏离平衡位置,考虑结构对称性和流速方向,其坐标系从o-xyz变化到o′-x′y′z′。把沿z方向的纵荡运动和绕x轴的纵摇转动分别化为只含有一个谐波项的函数[13],分别可以表示为
建立水中浮体在流场作用下的纵荡和纵摇运动动力学方程
3 作用力的求解
3.1 流场作用力的求解
流场作用力可以依据Morison 公式来计算[14],考虑浮体直径和流场深度之比,可以把浮体在流场中看作小尺度结构物,流场在浮体深度范围内的流速看作是均匀流速。流场作用力主要有沿流场速度方向的流体拖曳力Fd、浮体在y 方向的垂荡运动惯性力FIy和z方向纵荡运动惯性力FIz,流体绕流升力FL
3.2 系泊缆的动态伸长
水中浮体在受到流场作用力时,会偏离平衡位置,如图2 所示,系泊缆发生动态伸长,其约束力会出现变化,考虑变形协调条件,装置在流场作用下达到新的平衡位置时,系泊缆还是处于张紧状态,设系泊缆的变形为u(t),处于初始平衡位置时缆索长度分别为l1及l2,变形后的长度分别为及可得
式中:
u1(t)—系泊缆在角度θ1下的弹性变形量,m;
u2(t)—系泊缆在角度θ2下的弹性变形量,m;
θ1,θ2—系泊缆索偏移角度,(°);
Y(t)—y 方向的垂荡运动位移,m;
Z(t)—z方向纵荡运动位移,m。
考虑系泊缆和浮体连接位置铰接连接间隙,如图5 所示,在流场作用下,系泊缆动态伸长的长度变化范围分别为
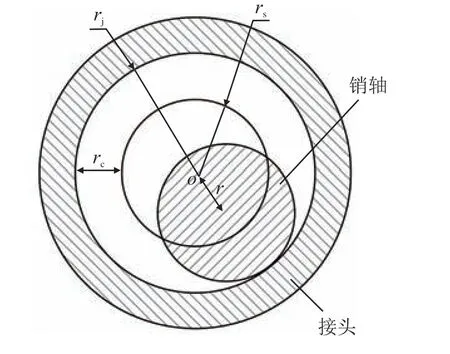
图5 间隙放大图Fig.5 Enlargement drawing for joint clearance
3.3 间隙磨损下系泊缆长度变化
由于连接部位销轴和轴套内壁之间通过法向接触碰撞力和切向摩擦力相互约束,在长时间的运动过程中,会出现黏滞,进而产生磨损。工程上对于磨损及磨损量的计算主要采取3 种方法[15],分别是Archard 黏着磨损计算方法、经验计算法和克斯盖尔斯通用磨损计算方法。Archard 黏着磨损计算方法国内外学者都做了很多研究[16],在参数的取值上都方便得多,其适用范围主要是弹性磨损,符合本文研究的销轴、轴套的接触磨损分析。Archard 黏着磨损量的计算方法为
式中:W—磨损量,m;
A—磨损系数,无因次,与材料特性相关,可以通过查阅文献得到[17];
s—销轴和轴套在一定磨损时间内的相对运动距离,m;
HB—材料的布氏硬度,N/m2;
p—根据赫兹公式得出的计算应力,Pa;计算公式为
式中:E1,E2—销轴和轴套的弹性模量,Pa;
µ1,µ2—销轴和轴套的泊松比,无因次;
FP—销轴宽度方向单位长度的接触力,N,可以通过仿真分析的方法求出,假设销轴和轴套在磨损范围内的磨损量均匀,磨损量和半径的变化关系为
式中:n—磨损次数,无因次;
b—轴套宽度,m;
∆r—磨损部位半径变化量,m;
ϕ—销轴和轴套的相对转角,(°),可以通过理论计算或仿真分析的方法求出。
∆r可以表示为
因此,考虑磨损后系泊缆的长度变化范围为
求解出系泊缆的动态伸长,根据材料力学理论,可以求解出浮体受到系泊缆约束力的变化范围。
3.4 方程求解
化简式(3)、式(4),可以得到
采用多尺度法来进行求解,引入小参数ε,设0 <ε ≤1,令u1=,比较ε 的同幂次项系数,消除永年项和长期项,得
4 模型参数
如图1 缆系式水中浮体的总装示意图所示,本文给出了一些缆系式水中浮体的尺寸参数、水动力学参数、材料参数及连接部位结构参数,具体数值如表1 所示。
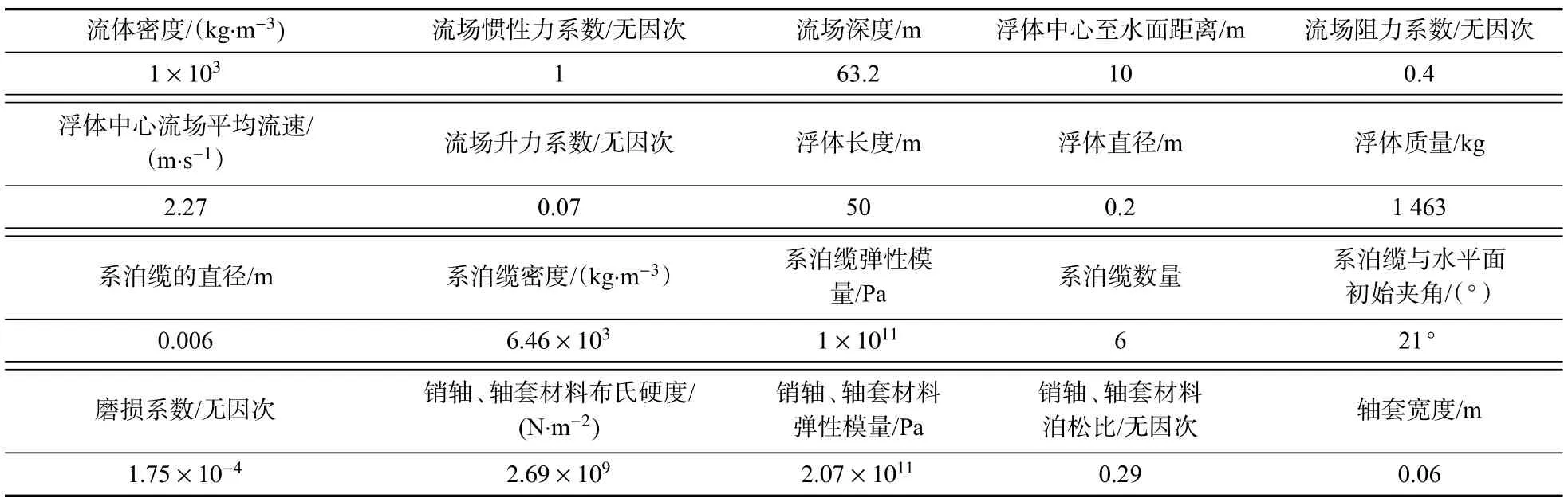
表1 模型参数Tab.1 Model parameters
5 磨损分析
图6 为销轴和轴套的相对转角,从图6 可以看出,受到流场作用力时,销轴和轴套的相对转角呈动态变化的情况,表明在运动过程中二者的接触范围和接触力也是变化的,运动过程中相对转角最大值达到23◦,其后随着时间的变化,相对转角在16◦左右波动。
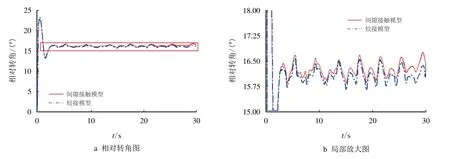
图6 销轴和轴套的相对转角Fig.6 Relative angle of axis pin and shaft sleeve
图7 为A 侧和B 侧销轴和轴套部位接触力响 应时程曲线图。
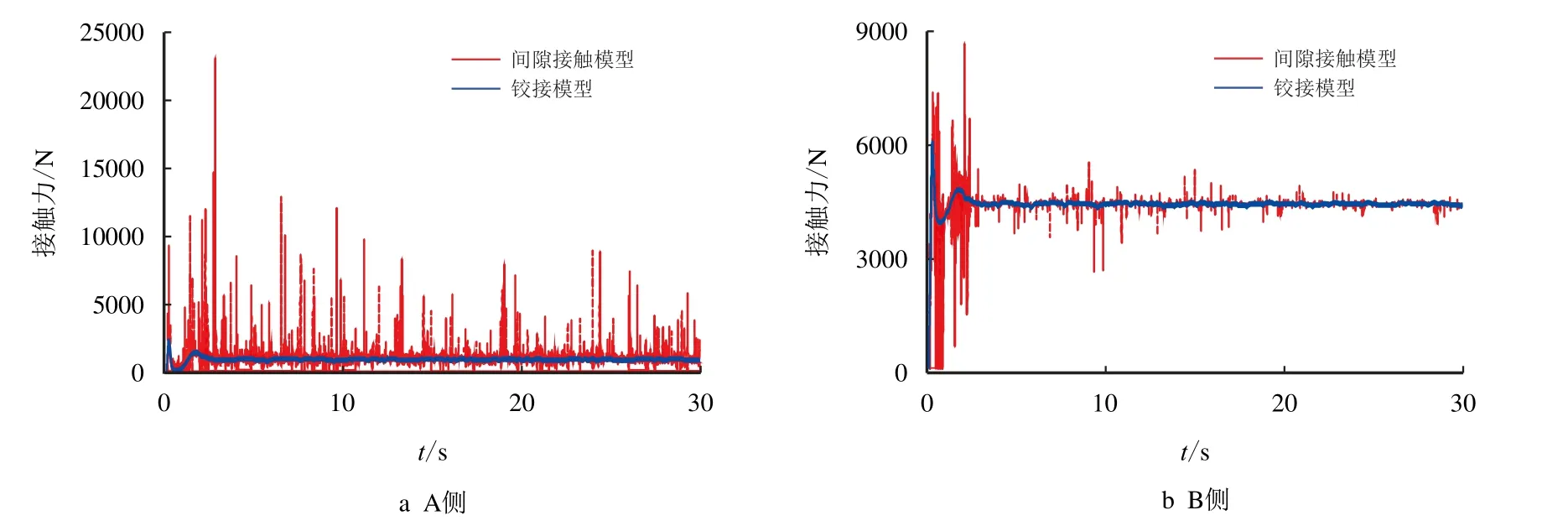
图7 接触力响应时程Fig.7 Time-distance graph of contact force for structure
由图7 可知,理想接触铰接模型中接触力最终会稳定在一个确定的值。考虑间隙磨损时,在流场作用下,销轴和轴套部位A、B 两侧接触力是不一样的,B 侧较大,接触磨损也会严重,因此,本文主要研究B 侧销轴和轴套在磨损过程中的接触力的变化和磨损深度变化。
磨损过程,销轴和轴套的接触条件和接触位置是不断变化的,不同接触位置的接触力也是不断变化的。在计算磨损量时,采取足够小的步长,相当于把相对运动转角等分为足够小的等份,每等份作为一个计算点,在计算点内认为接触条件相同,接触力保持不变,分别计算不同位置的接触力和磨损量,具体流程如图8 所示。
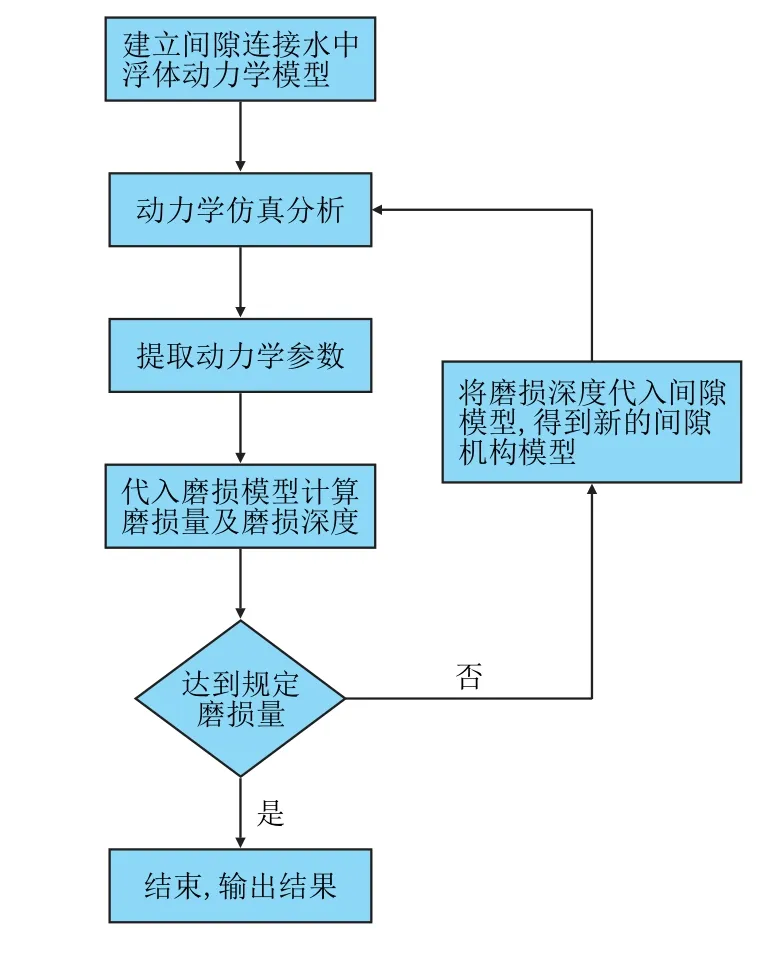
图8 磨损量分析流程图Fig.8 Flow chart of wear extent analysis
图9 和图10 分别提取了轴套磨损量为0、1.50、3.00 和4.50 mm 时铰接部位A、B 两侧的接触力变化曲线,从图9 和图10 可以看出,初始没有磨损量时,结构体刚开始运动时会有一个冲击力,以后一直稳定在954 N 和5 000 N 左右;随磨损量的增加,销轴和轴套的接触力也不断变化,呈现增加的趋势,当磨损量达到4.50 mm 时,A、B 两侧的最大接触力分别达到了11 968 N 和27 262 N,分别达到了理想铰接值的12.0 倍和5.5 倍。由于磨损量增加导致接触力的变化加剧,因此,就会使加速度、速度呈现出同样增加且不稳定的变化趋势,有可能导致结构的失稳,影响装置的功能。图11 和图12分别反映了B 侧轴套和销轴在不同转角位置时的磨损量,可以看出,随着销轴、轴套相对转角的变化,磨损量也会变化,最大磨损量出现在15◦左右的位置,这个位置也是销轴和轴套从静止开始运动,最终达到相对稳定时的位置。
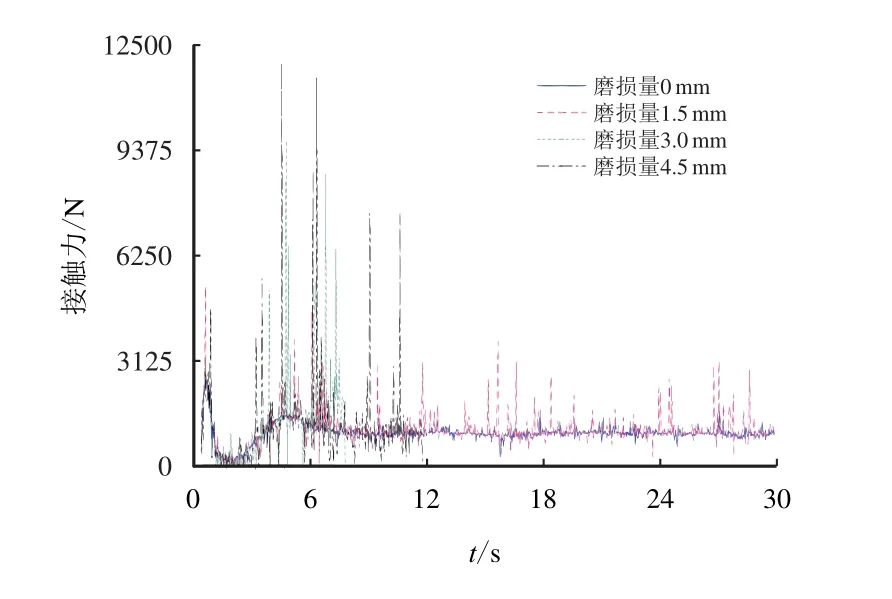
图9 A 侧销轴和轴套部位磨损过程中接触力响应时程Fig.9 Time-distance graph of contact force for structure in wear process of axis pin and shaft sleeve on side A
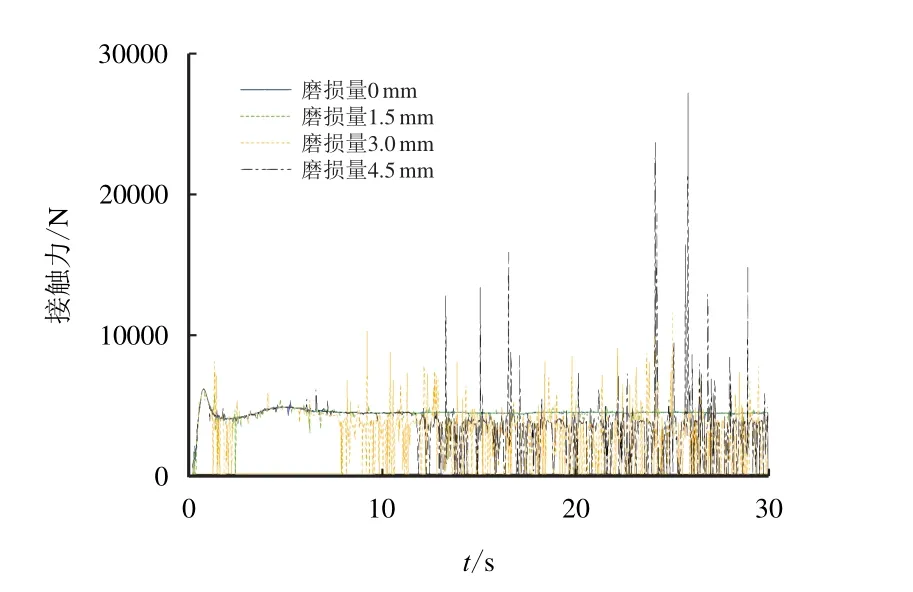
图10 B 侧销轴和轴套部位磨损过程中接触力响应时程Fig.10 Time-distance graph of contact force for structure in wear process of axis pin and shaft sleeve on side B
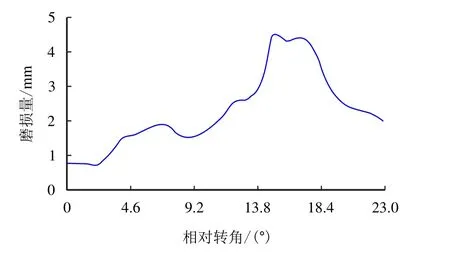
图11 轴套磨损量Fig.11 Wearing extent of shaft sleeve
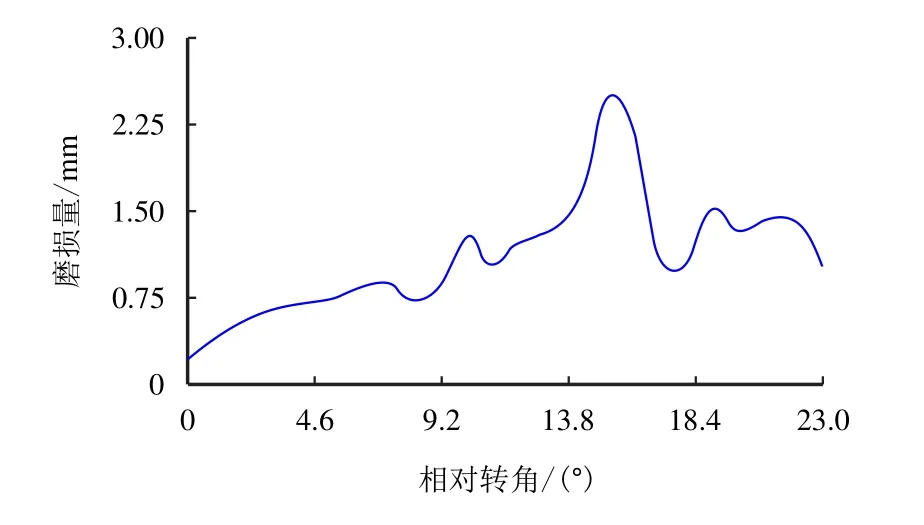
图12 销轴磨损量Fig.12 Wearing extent of axis pin
6 浮体功能可靠性分析
6.1 功能函数
考虑连接间隙磨损时,浮体的垂荡位移和纵摇角度必然为随机不确定性的,其可靠度可以定义为实际值偏离允许值误差的概率,假设浮体的允许值误差为∆v,可以建立可靠度功能函数为
式中:
vc—考虑连接间隙磨损时某时刻浮体实际垂荡位移,mm;
vl—浮体垂荡位移最大允许值,mm。
当g(v)>0,满足可靠性要求,当g(v)≤0,不满足可靠性要求,因此,垂荡位移或纵摇角度不满足可靠度要求的概率可以表示为
6.2 可靠度
考虑连接间隙磨损的水中浮体动力学广义方程,根据系泊缆长度的区间变量范围采用Newmarkβ 方法的逐步积分步长∆t和积分区间T,可以得到浮体垂荡位移或纵摇角度的分布参数[18]
式中:
i—计算次数;
u—某时刻浮体理想垂荡位移,mm;
σ2—纵摇角度的方差。
一般认为系泊缆长度的变化及磨损量服从正态分布,正态分布的叠加仍然服从正态分布,从而浮体垂荡位移和纵摇角度的误差也服从正态分布[19],则浮体垂荡位移或纵摇角度的可靠度可以表达为
式中:
u0—浮体垂荡位移允许极限值的均值,mm;
σ0—浮体垂荡位移允许极限值的方差。
图13 给出了考虑连接间隙磨损时浮体纵摇角度随时间的响应历程,提取了磨损量为0(理想铰接)、1.50、3.00 和4.50 mm 时的曲线,从图13 可以看出,随着磨损量的增加,浮体的纵摇角度在开始达到平衡位置之前都呈现增大的趋势;磨损量小于1.50 mm 时,浮体纵摇角度基本和理想铰接相吻合,稳定在16.0◦左右,超过1.50 mm 后,随着磨损量的增加,浮体纵摇角度呈现出波动的状态,当磨损量达到4.50 mm 时,最大纵摇角度达到31.5◦,达到理想铰接值的2 倍。图14 为纵摇角度均值,从图14 可以看出,磨损量小于1.50 mm 时,纵摇角度均值为16.0◦,磨损量超过1.50 mm 后,纵摇角度均值呈现急剧增大的趋势,根据式(30),可以求出浮体纵摇角度的可靠度随磨损量变化的曲线如图15 所示,可以看出,磨损量小于1.50 mm 时,可靠度的变化非常小,当磨损量大于1.82 mm 时,可靠度小于90%,浮体在工作过程中就有可能不满足功能的需求。
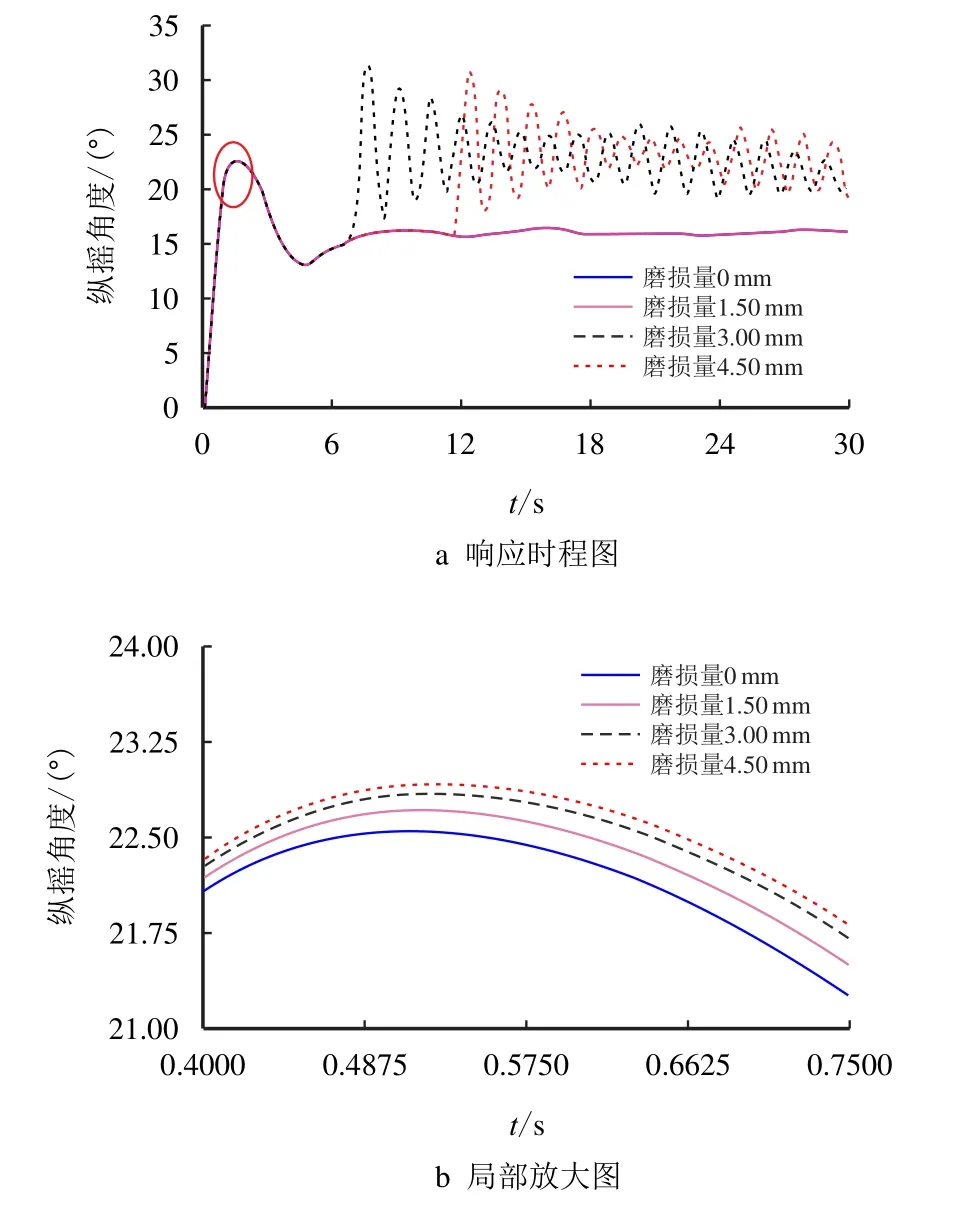
图13 浮体纵摇角度响应时程Fig.13 Time-distance graph of rolling angle response
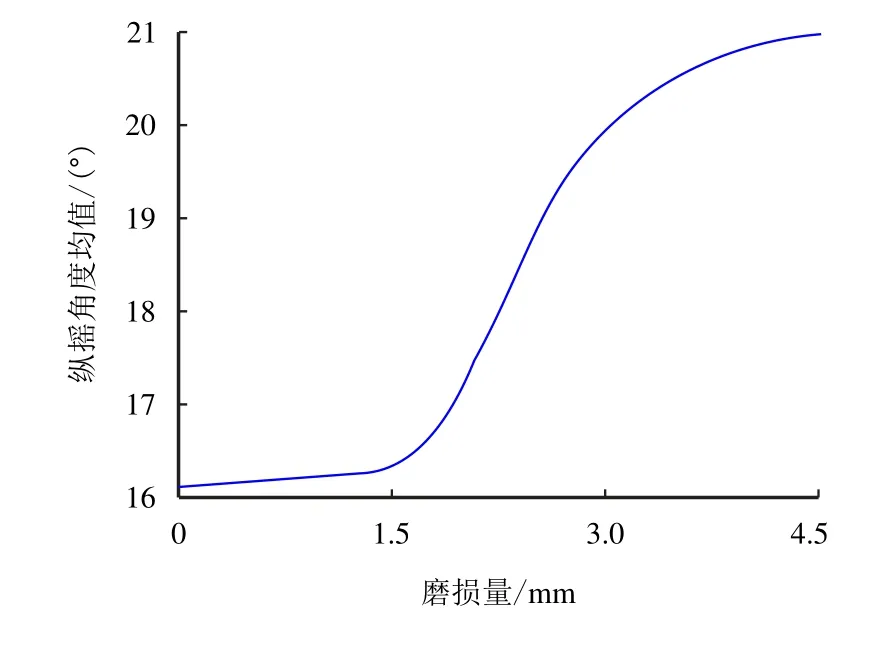
图14 纵摇角度均值Fig.14 Average value of rolling angle
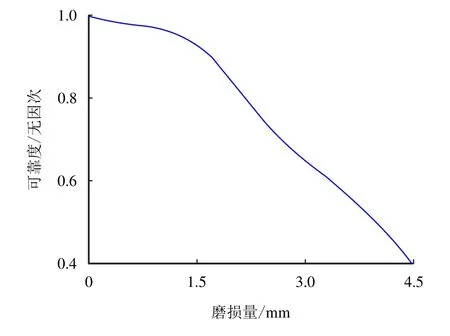
图15 浮体纵摇角度可靠度曲线Fig.15 Roll angle reliability curve of floating body
图16 给出了连接间隙磨损模型和铰接模型浮体纵荡位移随时间变化的响应历程,由图16 可见,浮体的位移响应随时间的变化幅度不大。图17 给出了在不同磨损量时浮体位移均值曲线,可以看出,在不同磨损量情况下,浮体位移均值几乎没有变化。
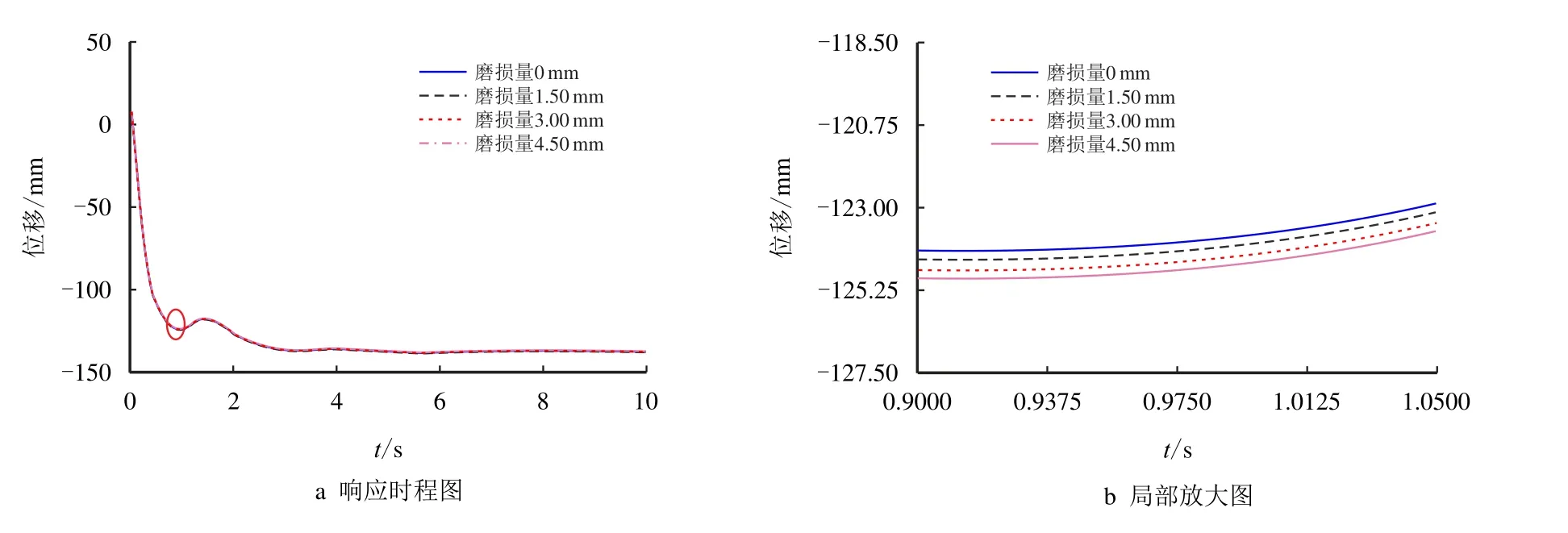
图16 浮体纵荡位移响应时程Fig.16 Time-distance graph of displacement response on the surging
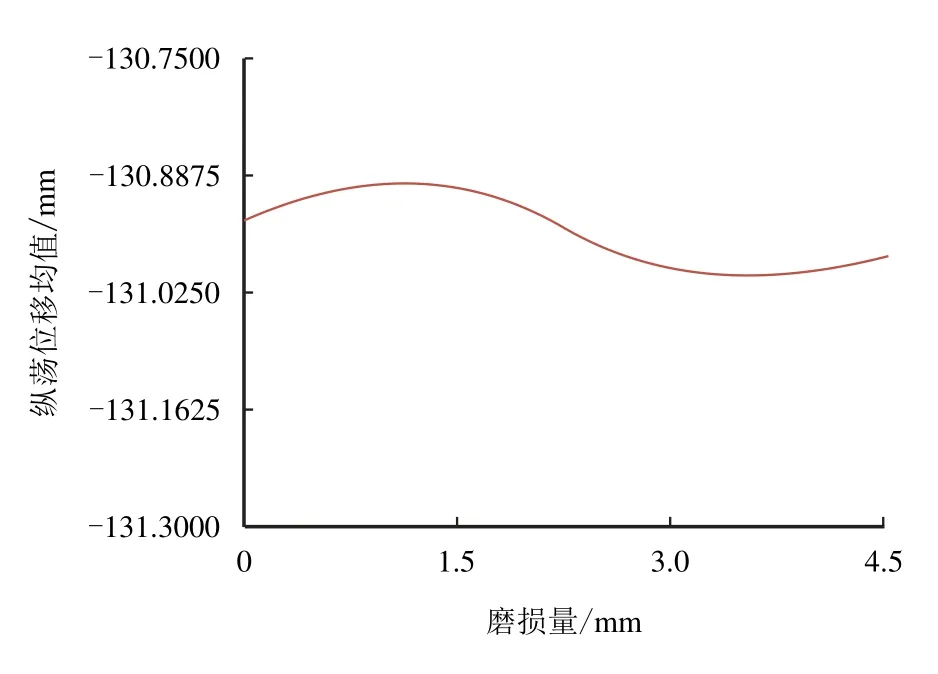
图17 纵荡位移均值Fig.17 Surging average value of displacement
图18 给出了在不同磨损量时浮体纵荡位移可靠度曲线。结果表明,磨损量在0∼3.00 mm呈直线下降趋势,可靠度降低较快。磨损量在3.00∼4.50 mm,可靠度趋于平稳状态。与理想铰接模型相比,间隙磨损模型的位移可靠度还是有一定程度的降低,但是仍然维持在96%以上。
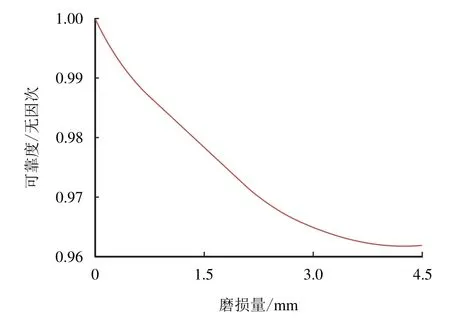
图18 纵荡位移可靠度曲线Fig.18 Surging displacement reliability curve of floating body
7 结论
1)随着磨损量的增加,销轴和轴套连接部位的接触力呈现急剧增加,出现很大的峰值,分别达到了理想铰接值的12.0 倍和5.5 倍,这有可能会在连接处产生瞬态断裂,破坏连接的可靠性。
2)销轴、轴套相对转角不同的部位,磨损量也不同,最大磨损量出现在运动达到相对稳定时转角为15◦左右的位置。
3)当连接磨损量大于1.50 mm 时,纵摇角度可靠度呈现出急剧的降低,当磨损量大于1.82 mm 时,纵摇角度可靠度小于90%。
4)间隙接触状态下浮体纵荡位移的可靠度也会出现一定程度的降低,总体来讲变化不大,对这类结构的研究,其纵荡位移的可靠性可以满足。
