基于井下环空参数的溢流智能预警技术研究

2023-05-10肖国清肖小汀邓红霞

西南石油大学学报(自然科学版) 2023年2期

葛亮，滕怡，肖国清，肖小汀，邓红霞

1.西南石油大学机电工程学院，四川成都 610500；2.西南石油大学人工智能研究院，四川成都 610500；3.西南石油大学化学化工学院，四川成都 610500；4.西南石油大学电气信息学院，四川成都610500

引言

随着全球油气勘探开发逐渐向复杂地层发展，在深层位和恶劣的环境下钻井极易发生井喷[1-2]，井喷的预防与控制成为世界油气田安全开发亟待解决的重大难题[3]。溢流是井喷的前兆，对井下溢流的监测及预警研究是防止井喷及正确制定压井方案的重要条件[4-5]。

为了实现早期溢流预警，国内外研究人员在随钻过程中通过井下仪器实现井下参数测量[6-10]，根据井下参数的相关特征获取溢流征兆，从而判断溢流与否。基于不同参数测量方法，各类溢流预警技术应运而生。目前，钻井中最常用的是基于综合录井数据的溢流预警技术，国外该方面的技术相对较成熟，国内戴永寿、孙合辉和周英操等基于该技术研究实现了油气井早期溢流在线监测与预警[11-13]，即先对溢流表征的规律参数进行阈值设定，若实测规律参数超出设定的阈值，工程师将对规律参数的数据进行处理分析，从而判断是否发生溢流并确定溢流类型。但是，阈值设定人为因素干扰较强，更多地依赖于现场工程师的专业能力，导致准确度与及时性不足，特别是钻遇复杂地层或油气储层时，需要多方技术人员现场支持才能完成。

针对这些问题，国内外大量研究学者将人工智能算法应用到石油钻井领域的溢流预警中。2001 年，Hargreaves 等基于贝叶斯概率模型计算得到深海钻井溢流发生的概率[14]；2008 年，Nybo 等将BP 神经网络对钻井溢流情况进行预警，但采用的是静态神经网络计算，并没有对数据进行实时动态计算[15]；2016 年，张禾等基于模糊专家系统和溢流表征规律建立了溢流预警模型，实现溢流与非溢流的判断[16]；2020 年，郭振斌等基于EKM 溢流预警系统采集井口进出口流量，通过累计流量对比实现溢流与漏失的监测[17]。

调查研究显示，大多预警系统基于地面参数进行溢流预警，其预测准确度具有一定局限性，且未对溢流严重程度做出判断。因此，本研究基于井下环空流量系统及其他测量系统监测近钻头处的环空参数，结合随机森林良好的模式识别和趋势预测性能，建立相应的溢流预警模型，并对溢流严重程度做出等级划分，通过搭建模拟实验平台完成方法验证，可以为后续预防井喷事故、实现安全井控提供指导。

1 预警模型建立

1.1 溢流参数选择

溢流是多种因素综合造成的，其发生时井下和井面的相应参数会发生变化。由于地面参数的一些局限性，对近钻头处参数的直接测量可以更及时更精准地辨别是否有溢流风险。近钻头的参数主要有流量、压力、温度、电导率和中子孔隙度等。本文基于环空电磁流量系统和其他测量系统，得到了较稳定和准确的环空流量值、环空压力值和环空温度值。通过搭建模拟平台对水侵进行模拟分析，发现溢流发生时环空压力和温度都随溢流量的增加而有较明显的变化趋势。

因此，经过对溢流后相关征兆参数的变化分析，本文选择基于环空流量、环空压力和环空温度3 个征兆参数建立溢流预警模型。

1.2 溢流智能预警模型建立

在溢流发生时环空温度和环空压力不同程度地升高、环空流量不断增加，溢流与这些征兆参数之间存在某种非线性的关系，无法建立具体的数学表达式。因此，找出征兆参数与溢流风险之间的联系是预警的关键。而机器学习中的随机森林算法具有良好的模式识别和趋势预测性能，它学习速度快，并可很大程度上防止模型出现过拟合现象。因此，本文选用随机森林算法研究井下溢流，可同时满足快速性和稳定性的要求。

随机森林以CART 决策树为基础，它利用属性的不同取值对数据进行分类预测，采用自顶向下的递归方式，从根节点开始，在它的内部节点上进行属性值的测试比较，每次选择Gini 信息增益最小的分支作为下一个根节点，最后在决策树的叶子节点得到结论[18-20]。为了精确地定义信息增益，需要定义信息熵，它刻画了任意数据集的纯度。如果溢流风险类型具有M个类别，那么样本数据集D相对于M个类别的熵定义为

式中：

Ent—熵；

D—溢流样本数据集；

M—溢流风险类型的类别个数；

Pm—第m类风险的样本数占总样本数的比例。

已有了熵作为衡量训练样本纯度的标准，信息增益

式中：Gain—信息增益；

a—环空参数；

Dj___将某一种环空参数按照数值大小进行二叉树分类中，分为第j类的数据子集。

用信息增益作为属性值的划分会导致确定节点时偏向于选择取值多的属性值。因此，最优节点的划分常采用信息增益率作为判断准则[18]，信息增益率是用信息增益和信息熵共同定义的

式中：Ration—信息增益率；

Iv—信息熵。

以环空参数a划分的信息熵Iv（a）为

然而，单个决策树在产生决策判断时具有很强的随机性和主观性，造成误判的可能性较大，且极易受噪声扰动的影响，其算法稳定性不高。因此，在单个决策树的基础上衍生出多棵决策树，就形成了随机森林。研究表明，随机森林可以提高分类或预测的精度，从而提高算法的稳定性和准确率[21-22]。

随机森林算法基于Bootstrap 方法重采样，即在构建决策树时采用随机选取分割属性、随机选择数据的方法，使每棵决策树在各个参数属性层面上平等[23-25]。若数据集S中有n个不同的样本[X1,X2,···,Xn]，每次有放回地抽取一个样本，抽取n次后生成新集合S∗，则S∗中不包含某个样本X（ii=1,2,···,n）的概率为

当n趋于无穷时

该结果的含义是：在平均情况下，新集合S∗中仅包含了原集合S中约100.0%-36.8%=63.2% 样本，而其他36.8%的样本将形成检验集。这样做不仅解决了由于单个决策树产生的不稳定问题，也可以提高预测结果的稳定性[24-25]。

预警模型方法示意图见图1，该模型的输出对溢流严重程度做出了等级划分。一般在现场操作中认为将溢流量控制在2 m3前发现比较安全[26]，但由于溢流严重程度受诸多复杂因素的影响，目前还没有明确和统一的标准作为其严重程度划分的依据。因此，根据本文溢流模拟装置的流量入口尺寸和侵入流体流速，经过计算，按照侵入流体的体积量将溢流严重程度分为4 个阶段，其对应关系与模型输出编码见表1。

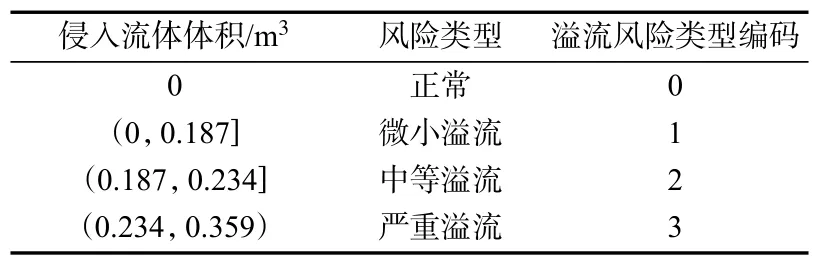
表1 溢流严重程度划分与模型编码Tab.1 Overflow severity classification and model coding

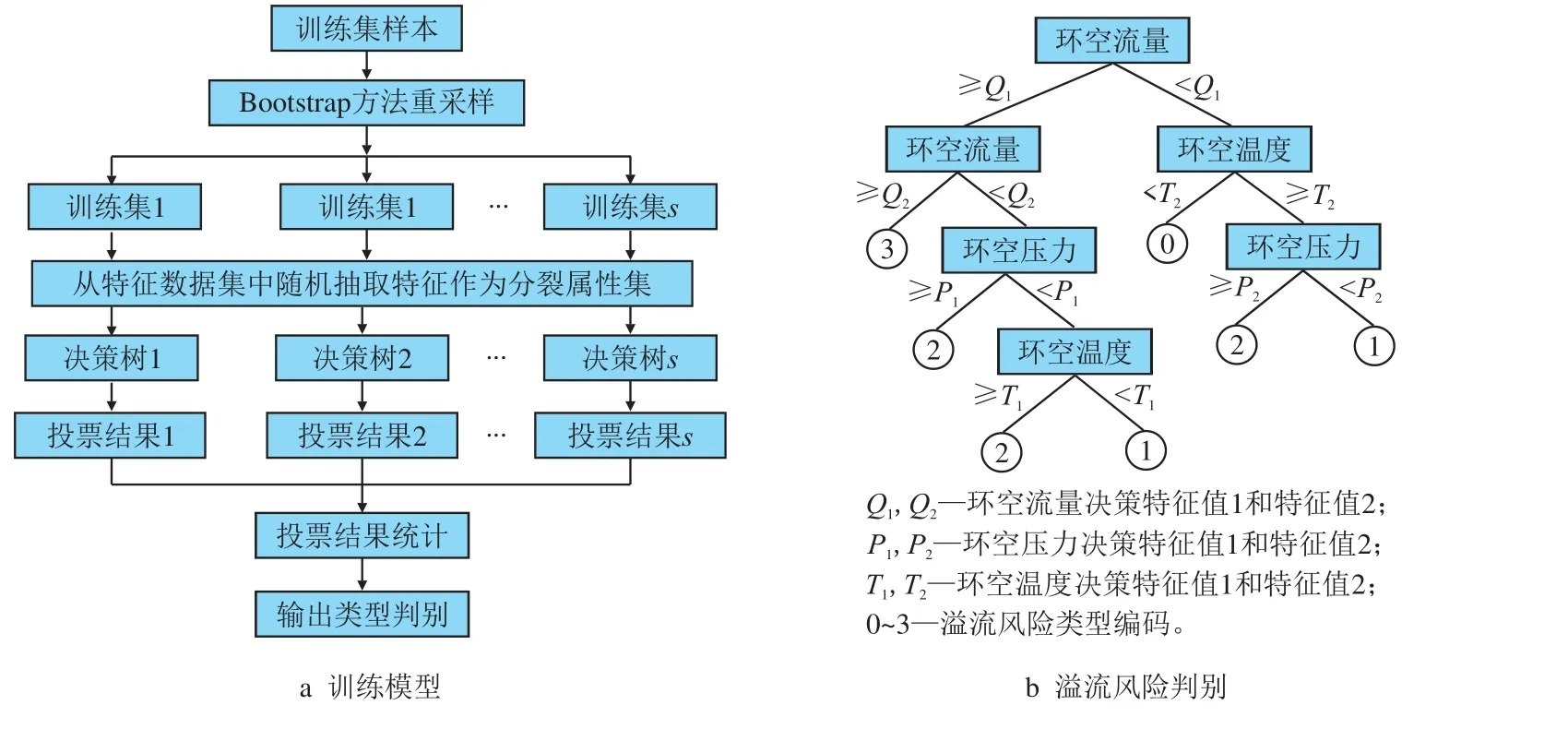
图1 随机森林溢流预警模型方法示意图Fig.1 Prediction method for overflow warning based on random forest

因此，模型中将溢流的判识问题建模成以3 种环空参数为输入变量、溢流风险类型为预测结果的预警模型，测试集样本经过Bootstrap 重采样产生s个训练子集，对应生成s棵决策树，每一棵树都会对输入量进行投票，最终将投票多的那一类作为该输入量的最终决策结果。

2 实验验证与结果分析

2.1 实验平台搭建

为了验证本文提出的溢流预警模型，构建溢流模拟平台，研究拟实现的溢流模拟系统的框架图如图2 所示，该系统主要由主循环模块、气侵模拟模块和液侵模拟模块构成。

在模拟溢流情景时，气侵模拟模块和液侵模拟模块用于模拟地层气体和液体的侵入，电磁阀用于控制气体或者液体的注入，气体或液体流量计用于测量注入的气体或液体的量，温度传感器和压力传感器用于监测注入的气体或者液体的温度和压强，加热器和压缩机用于提供相应的气体或液体的温度和压强。

2.2 实验与结果分析

实验中，在储存罐中注入盐水，开启电机使流体进入正常循环，开启预警监测系统，等待系统循环进入平稳阶段后开启液侵阀门，从外部注入65◦C的纯水，从而使系统中产生模拟液体侵入的情况。流体流速如图3 所示。

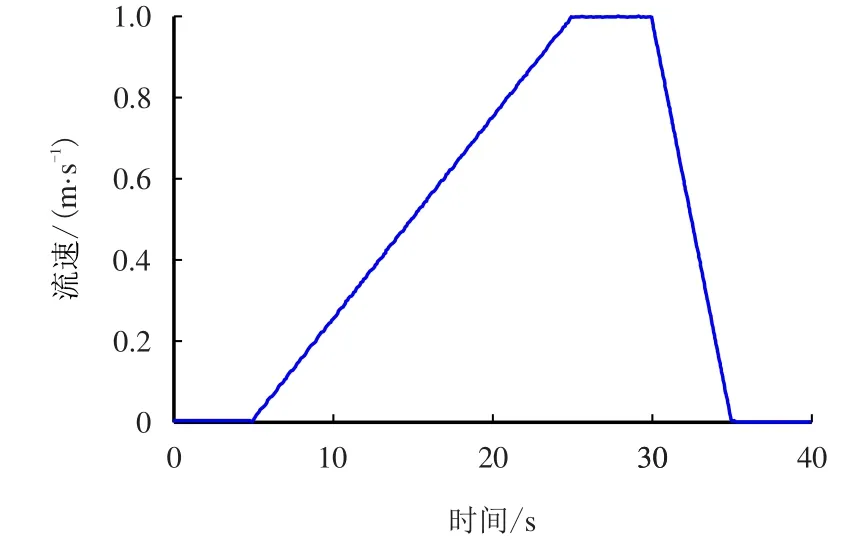
图3 侵入流体流速变化图Fig.3 Intrusion fluid flow rate change graph

通过对实验进行多次测试，收集到109 组环空流量、压力及温度的样本数据，剔除缺失、冗余数据后，最终选取51 组数据作为训练样本，41 组数据作为测试样本来对本文提出的溢流预警模型进行训练和验证。

在模拟平台中进行实验，让液侵阀门在第5 s时开启，持续30 s，在第35 s 关闭，模拟液侵发生过程，液侵模拟监测到环空流量、环空温度和环空压力的变化如图4 所示（其中，1 psi=6.895 kPa），当溢流发生时环空压力、环空温度及环空流量曲线开始逐渐上升，当关闭液侵阀门时，各项数值逐渐回归。

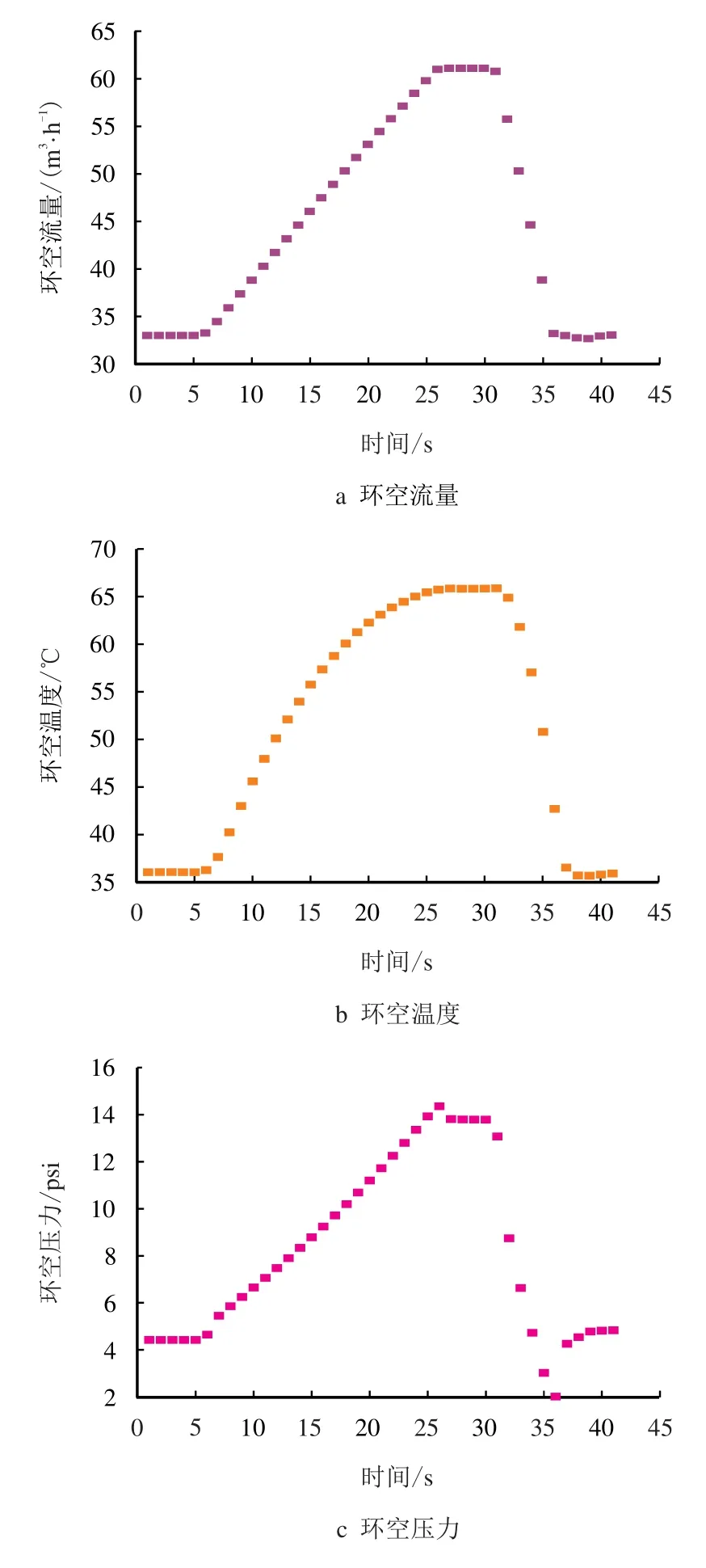
图4 液侵时环空压力、温度和流量的变化图Fig.4 Changes of annular pressure,temperature and flow rate during liquid intrusion

模拟液侵的同时，将数据实时输入到溢流预警系统中进行溢流等级的判断。在随机森林预警模型中，决策树以X1,X2,X3分别表示井下环空流量、压力和温度，构建决策树如图5 所示。

由于分类器将样本中最重要的特征作为根节点，由图5 可知，此次训练将X1即环空流量作为判断溢流最重要的决策特征。

然而，用这样完整的树来预测很可能造成过拟合，因此，通过观测交叉验证误差随决策树叶子节点个数变化情况来判断最佳的叶子节点个数。变化趋势如图6 所示。

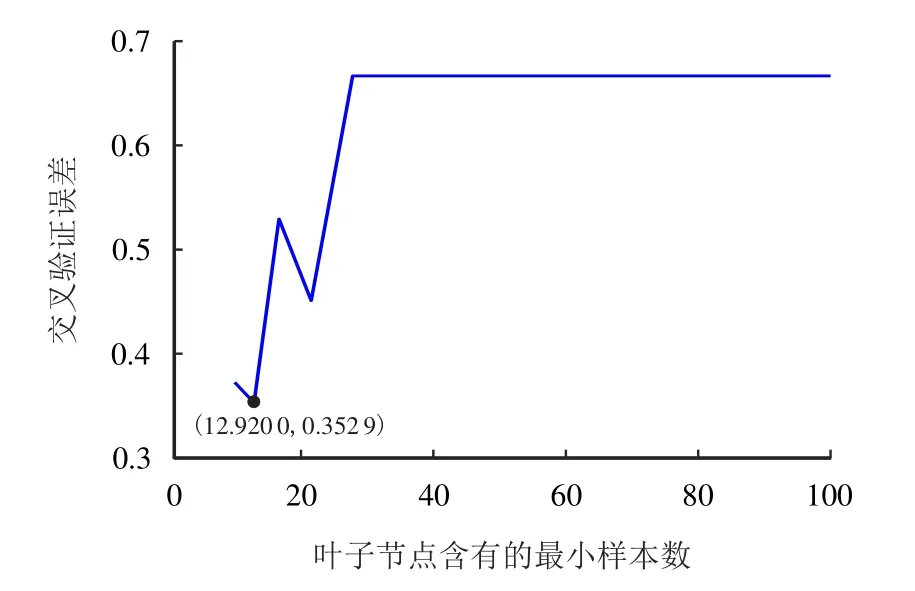
图6 叶子节点个数对决策树误差的影响Fig.6 Influence of number of leaf nodes on the error of decision tree

随着决策树个数的不断增加，交叉验证误差最小点的坐标为（12.920 0，0.352 9），表明在该次预测中，当叶子节点含有的最小样本数为13 时，该树模型的交叉验证误差最小，预测效果最佳，可有效降低预测集本身的随机性为模型结果带来的不稳定。当限制叶子节点的数目为13 时，得到的树模型如图7 所示。

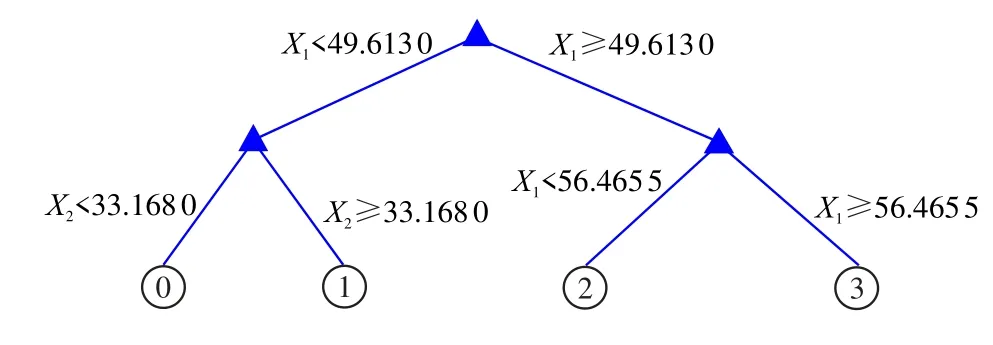
图7 最佳叶子节点数时的树模型Fig.7 Tree model with optimal number of leaf nodes

比较限制叶子节点前后的交叉验证误差，优化前决策树的误差为0.163 1，优化后决策树的误差降为0.119 4，优化后决策树的性能有所提升。

为了进一步提升系统性能，在决策树的基础上建立了随机森林模型。对于随机森林模型，其性能与精度直接受决策树个数的影响，个数过多会造成模型成型慢且易产生过拟合，个数过少则会导致建立的模型精度低，数据利用不充分[23]。为了有效利用数据，研究了决策树棵数对随机森林性能的影响，从而确定决策树的优选范围。预测正确率与树的棵数之间的关系如图8 所示。

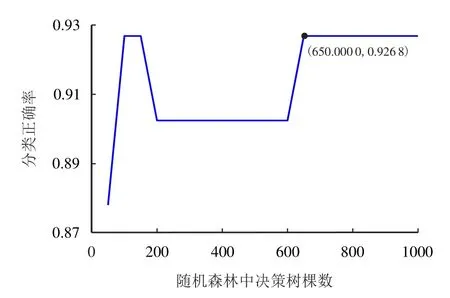
图8 决策树棵数对性能的影响Fig.8 Impact of decision tree number on performance in random forest

当树的棵数为650 棵时，预测准确率已经达到最高92.68%且保持平稳。因此将决策树的棵数设置为650 棵，构建随机森林，经过训练样本后用测试样本检验模型的性能。

为了验证本文模型的优越性，将同样的样本数据输入到BP 神经网络系统中进行溢流预警结果的仿真和计算，测试结果如图9 所示。

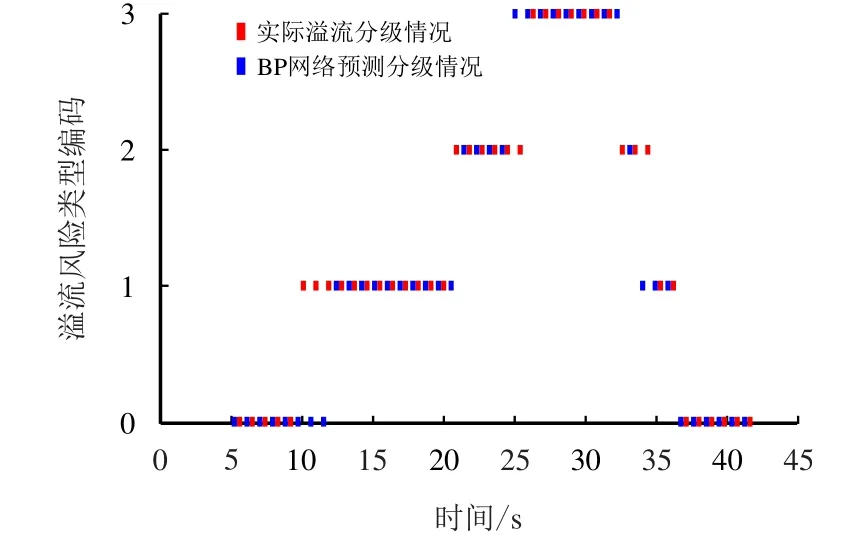
图9 BP 预测值与真实值对比图Fig.9 Comparison of BP predicted value and true value

由图9 可知，该BP 神经网络系统的分类预测结果为1 和2 时与实际分类情况存在不重合的情况较多，表明该系统对微小溢流和中等溢流的分类预测效果不佳。BP 神经网络与决策树、随机森林的测试结果如表2 所示。

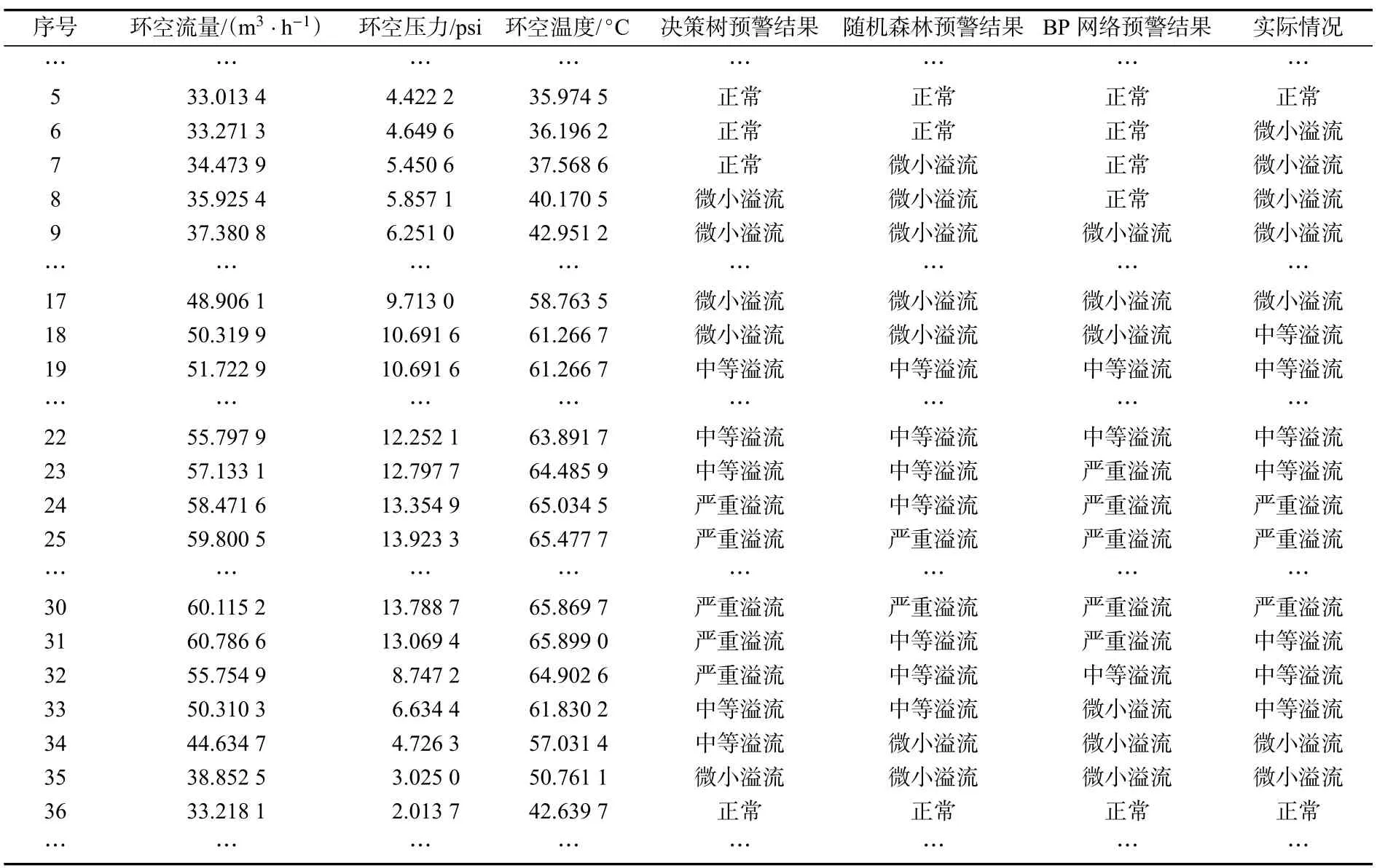
表2 预测结果对比Tab.2 Comparison of prediction results

3 种模型的分类预测效果对比如表3 所示，由表3 可知，3 种模型对微小溢流和中等溢流的分类正确率较正常和严重溢流的正确率降低，其中，BP神经网络分类模型的正确率最低。而基于树模型的决策树和随机森林的准确率整体上优于BP 神经网络，随机森林的预测准确率最高达到了92.68%，在进行溢流严重程度分类预测时稳定性最强、预测效果最好，能够满足大多数现场应用的需求。