集输管道CO2 腐蚀预测机理模型研究
2023-05-10蒋宏业刘映雪骆吉庆徐涛龙
蒋宏业 ,刘映雪,,何 莎,骆吉庆,徐涛龙
1.西南石油大学石油与天然气工程学院,四川 成都610500 2.中国石油川庆钻探工程有限公司安全环保质量监督检测研究院,四川 广汉618300
引言
CO2腐蚀是油气田地面集输管道较为普遍也是较为严重的腐蚀问题。随着中国碳捕集,碳利用与储存(Carbon Capture Utilization Storage,CCUS)技术的不断发展,CO2驱油技术在各大油田得到广泛应用,但同时也导致CO2作为伴生气对集输管道产生严重的腐蚀。可靠的腐蚀速率预测不仅是了解管道腐蚀程度的手段,也是油气生产中管道及相关设施设计的重要参考因素。CO2的腐蚀速率预测是管道腐蚀与防护的关键内容之一,具有重要的现实意义和经济价值。
在已有的研究中,根据实际现场数据或者实验数据建立了许多经验、半经验模型。其中,在工业领域应用较为普遍的是挪威的Norsok M-506 模型[1]。这一经验模型基于实验和现场数据建立,对腐蚀热力学及腐蚀动力学等理论计算考虑较少[2]。为了使模型适用于不同的生产环境,在Norsok 模型的基础上引入不同的修正系数,一定程度上拓宽了经验模型的应用范围[3-5]。20 世纪90 年代De Waard 等[6-12]提出的一系列半经验模型也得到了广泛的应用,但这些模型是理论和实验结合的产物,只适用于特定的环境,而随着油气行业的不断发展,面临的复杂生产环境使得这些模型应用受限,因此,对半经验模型的修正改进也十分有必要[13-15]。1996 年,Nesic 等[16]以腐蚀动力学为基础,建立了基于理论的CO2腐蚀预测机理模型。模型不依靠大量的实验或现场数据,基于化学、电化学计算和传质动力学理论来实现腐蚀速率的预测,其中,每个参数都具有理论意义,因此,在引入修正系数时可以根据环境条件的不同为每个参数引入特定的修正因子,这使得机理模型有很强的拓展性。模型前期对传质部分进行了简化计算,且未考虑腐蚀产物膜的影响,这些问题在作者之后的研究中得到了解决[17]。Nesic 等不断开拓新的影响因素,陆续将H2S、多相流、原油、腐蚀产物膜、水润湿效应及水冷凝作用等纳入机理模型中,建立了较为全面的CO2腐蚀速率预测综合模型[18-23]。Song[24]首次将O2和阴极保护对CO2腐蚀速率的影响引入到模型中,并考虑了CO2在边界层中的扩散反应。Elgaddafi等[25]指出利用亨利定律来计算溶解CO2以及其他腐蚀性物质在溶液中的体积浓度会导致预测结果的偏高,因此,提出了改进的溶解度预测计算模型,并用实验数据验证了该模型的准确性。
与经验、半经验模型相比,机理模型虽然涉及大量的理论计算,但能涵盖更广更复杂的条件,具有良好的灵活性和外推性。本文依据腐蚀热力学和腐蚀动力学理论,考虑流体流动、电化学反应及传质过程等多场耦合作用,在Nesic 等的研究基础上,引入腐蚀产物膜对离子传质扩散系数的影响因子(简称腐蚀产物膜影响因子),提出了新的腐蚀预测机理模型。利用活度系数、逸度系数和离子强度对CO2溶液体系的非理想性进行修正,利用Butler-Volmer 方程计算电化学反应腐蚀电流密度,并通过Nernst 方程和吉布斯自由能计算各阴极反应标准平衡电位,有效修正了产物膜存在下CO2机理模型预测值偏高的情况。
1 CO2 腐蚀预测模型的建立
基于Nesic 等的经典机理模型,本模型引入腐蚀产物膜影响因子,对传质极限电流密度计算进行了改进,提出腐蚀预测机理模型
模型考虑了H+、H2CO3及H2O 的还原反应和Fe 的氧化反应,各电极反应总电流密度由活化电流密度和极限电流密度共同决定,见式(1)。其中,活化电流密度和极限电流密度计算见式(4)和式(5)。根据钢表面电荷平衡方程式(2)可计算求解出腐蚀电位和腐蚀电流,最后,通过法拉第定律式(3)求解腐蚀速率。
2 CO2 腐蚀预测模型的计算
CO2腐蚀的本质是电化学反应过程,但是整个腐蚀体系中的反应离不开溶液化学以及传质过程的影响。本文将从溶液化学、电化学及传质3 方面对CO2腐蚀机理模型计算方法进行介绍。
2.1 溶液化学计算
很多机理模型在对CO2溶液体系进行化学平衡计算时将溶液和气体视为理想介质,但在实际情况下,水具有很高的溶解固体含量(>10%),CO2也并不是一种理想气体。因此,本文利用活度系数、逸度系数及离子强度对介质的非理想性进行修正,修正后二氧化碳饱和溶液中常见化学反应及其平衡常数计算见表1。

表1 CO2 饱和溶液中常见化学反应及修正后平衡常数计算Tab.1 Common chemical reactions in solutions saturated with CO2 and calculation of modified equilibrium constants
通过以上溶液化学平衡计算可得到随pH 值变化溶液中各离子浓度分布情况。对于开放系统,在25◦C,CO2分压为1 MPa 的条件下,理想CO2溶液中各物质离子计算浓度随pH 值变化见图1a,非理想溶液中离子浓度分布见图1b。
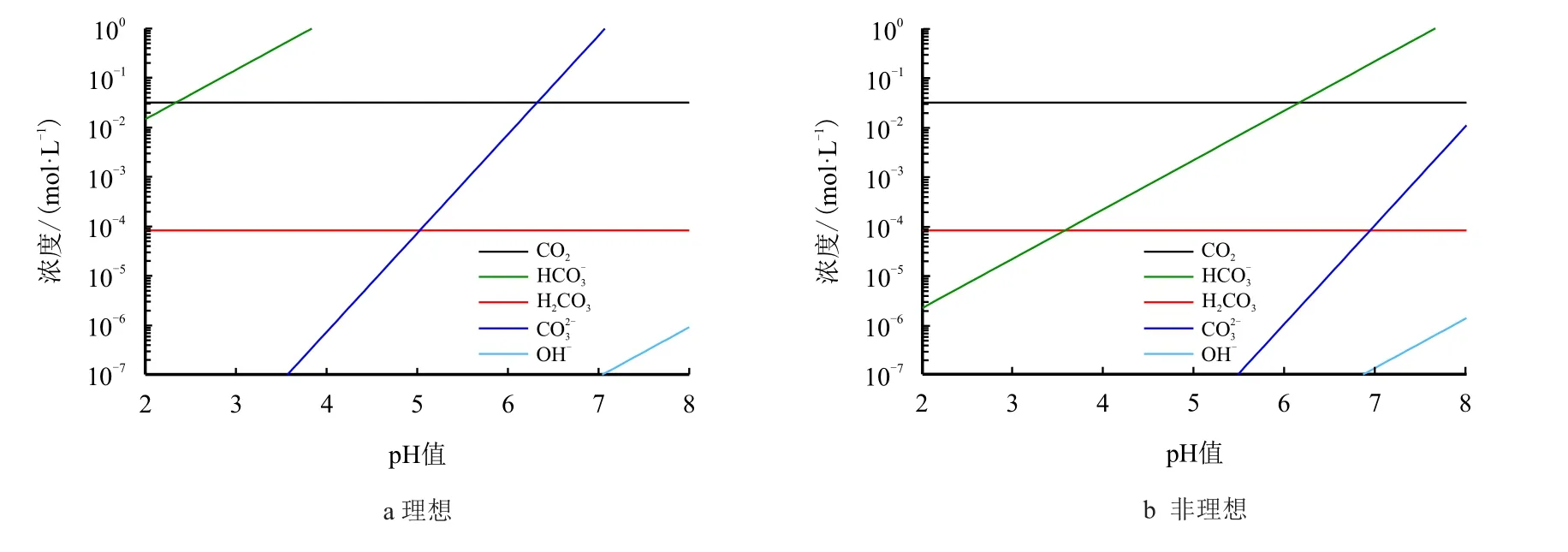
图1 CO2 饱和溶液中离子浓度随pH 值变化规律(pCO2=1 MPa,T=25 ◦C)Fig.1 Variation of ion concentration with pH in CO2 saturated solution(pCO2=1 MPa,T=25 ◦C)
计算结果表明,随着溶液pH 值的升高,溶液中各离子浓度均增大。不考虑气体和溶液的非理想性,将会导致计算所得离子浓度总体偏高,且溶液离子组成越复杂,计算离子浓度越低。目前,对于阴极反应中碳酸还原反应机制存在争议,其中,主要以碳酸直接还原和间接还原为代表[27]。若将碳酸还原视为间接还原,即H2CO3的第一步电离仅为反应提供H+,接着再进行的直接还原反应,那么的直接还原将成为影响腐蚀速率的关键步骤。由图1 可知,随着pH 值升高,浓度持续上升,腐蚀速率也应随之上升,而实际腐蚀速率并不会一直增加[28]。有研究认为,的直接还原反应速率相对较低,无论存在多少,都不能显著地促进整体腐蚀速率,在模型中可忽略不计[29]。因此,本文所建模型仅考虑阳极铁的氧化和阴极H+、H2CO3、H2O 的直接还原。
2.2 电化学计算
电化学反应的反应速率通常用电流密度来表示。由于已有研究所沿用的Tafel 方程具有一定的理想性,当电位达到平衡电位时电流密度为零,且会导致阴极电位的预测偏高和阳极电位的预测偏低,因此,本文采用Butler-Volmer 方程用以计算电化学反应的活化电流密度iα,见式(4),以便更真实地描述电流和电位的分布情况。以阳极反应为例,对Butler-Volmer 方程中交换电流密度进行计算,Fe氧化Tafel 曲线示意图见图2。
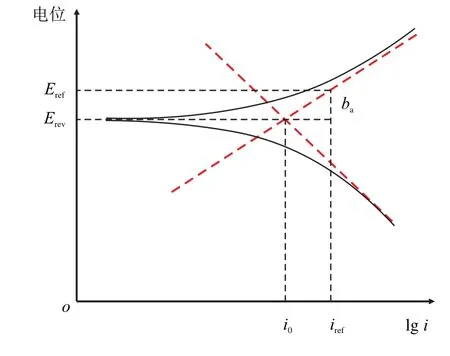
图2 Fe 氧化Tafel 曲线示意图Fig.2 Tafel diagram for Fe oxidation
根据Tafel 曲线斜率和参考电位电流可得
阳极氧化反应参考电位取−0.488 V,平衡电位由Nernst 方程进行计算,见式(7),参考电流密度和阳极Tafel 斜率计算见式(8)和式(9)。
将式(7)∼式(9)代入式(6),可得交换电流密度
Nesic 等在对各阴极反应平衡电位进行计算时,将H2CO3还原、H2O 还原的平衡电位等同于H+还原平衡电位,这在一定程度上减少了模型的计算,但降低了机理模型的精确性。为了使计算更为准确,本文采用Nernst 方程对各阴极反应平衡电位进行计算。其中,各反应标准平衡电位可根据反应的物质吉布斯自由能得到[26]
综上,以阳极反应为例,基于Butler-Volmer 方程的电化学反应参数计算见表2,阴极各电极反应交换电流密度和平衡电位计算方法同理,部分计算参数取值可参考相关文献[17,30]。

表2 基于Butler-Volmer 方程的阳极电化学参数计算Tab.2 Calculation of anodic electrochemical parameters based on Butler-Volmer equation
2.3 传质计算
图3 为腐蚀产物膜存在下离子传质示意图。在流动条件下,离子的传质主要受两方面因素影响:流体边界层对离子传质的阻碍和腐蚀产物膜对离子传质的阻碍。
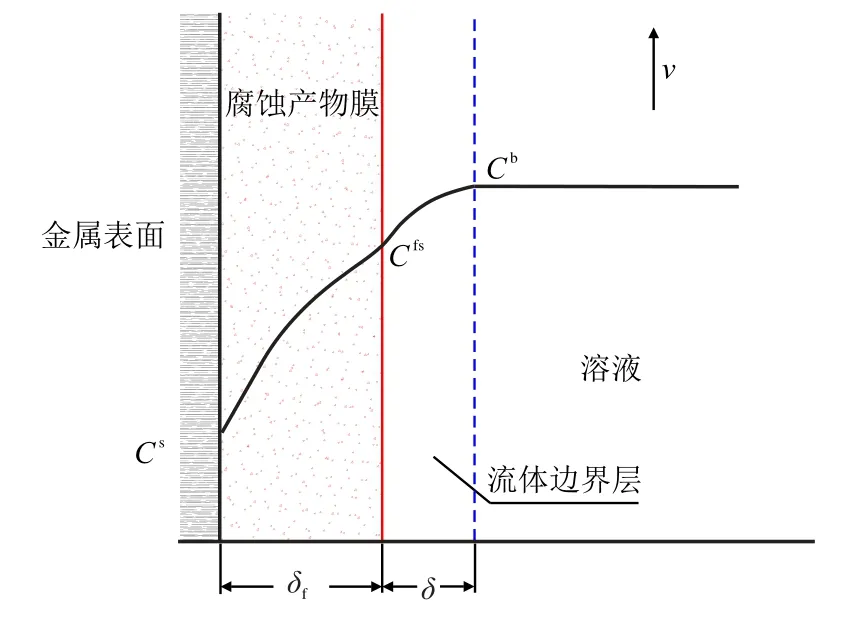
图3 腐蚀产物膜存在下离子传质示意图Fig.3 Diagram of ion mass transfer in the presence of corrosion product film
研究表明,影响腐蚀产物膜的保护性能因素为产物膜的致密度,因此,腐蚀产物膜厚度对腐蚀产物膜中离子传质并没有直接影响,在环境温度压力变化不大的情况下,腐蚀产物膜厚度可取定值。当金属表面离子浓度为零,此时有
2.3.1 流体边界层对传质的影响
H+离子还原主要受离子扩散传质的影响,在流体边界层内的传质速率为
2.3.2 腐蚀产物膜对传质的影响
在公开的文献中表明,多孔腐蚀产物膜中离子i的传质系数kf,i是扩散系数Di、孔隙度ε、弯曲度τ和厚度δf的函数[31]
那么,从本体溶液到钢表面的总传质系数kT,i则为溶液中的传质系数km,i和产物膜中的传质系数kf,i的函数
通过建立该模型求解各物种的质量守恒方程,从而得到钢表面所有化学物质的浓度,进一步得到反应的腐蚀电流、腐蚀电位、腐蚀速率等,计算过程复杂且难度较大。
目前,腐蚀产物膜对离子扩散的阻碍机制仍没有统一的观点。因此,本文通过拟定腐蚀产物膜影响因子简化传质计算
式中:
Df—离子在腐蚀产物膜中的扩散系数,m2/s。
忽略对流和电迁移的影响,离子扩散传质速率可通过Nernst-Planck 方程进行计算。腐蚀产物膜内传质电流密度计算见式(18)[32]。
2.3.3 极限扩散电流密度计算
将式(14)和式(18)代入式(13)中,得到腐蚀产物膜表面的离子浓度
继而求得离子传质扩散极限电流密度
若已知某一环境下腐蚀速率或腐蚀电位电流,在该机理模型中为唯一的未知数,因此,可通过现场获取的腐蚀速率对该影响因子进行计算。根据实际生产环境的不同,计算得到的腐蚀产物膜影响因子可作为温度、流速、pH 值、CO2分压及离子浓度等影响因素的函数,如式(21)所示,利用Boltzmann函数进行一元或多元非线性拟合得到相应腐蚀环境下的经验公式。
“这一点非常暖心,也非常有必要。”在某三甲医院医保办公室工作的刘怡告诉记者,如果纳税人得了大病,通常收入水平会下降,可能达不到扣税标准,享受不到相关扣除政策。允许配偶扣除,可以有效减轻纳税人所在家庭的负担。
3 预测模型有效性验证
为了验证模型的有效性与准确性,利用已有文献中实验测得的各项腐蚀数据,结合相应的腐蚀实验条件,对本模型的计算结果进行对比分析。涉及腐蚀电位均相对于标准氢电极的电位值。
3.1 极化曲线行为预测对比验证
利用所建立的机理模型对腐蚀过程中所参与的重要电化学反应的极化曲线进行预测,研究碳钢在不同温度、CO2分压等条件下的电化学行为,并与文献中实测动电位极化曲线进行对比分析。图4 为20 号钢在温度为25◦C、pH 值为5.38 的油田采出水环境下,动电位极化曲线实测值与未考虑腐蚀产物膜影响的模型预测值对比图。由于该条件下温度和CO2分压均较低,因此,可不考虑腐蚀产物膜的影响,令模型中腐蚀产物膜影响因子ffilm为1。
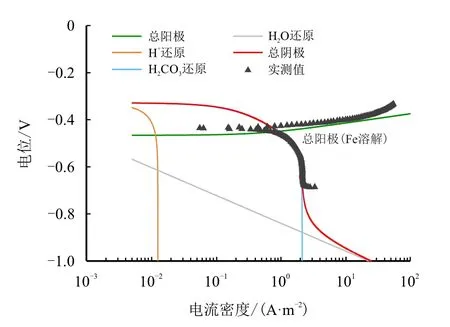
图4 动电位扫描极化曲线实测值[33] 和模型预测(T=25 ◦C,pH=5.38)Fig.4 Experimental data[33] and model prediction of potentiodynamic sweep(T=25 ◦C,pH=5.38)
由于实验所用介质呈弱酸性,因此,H+还原反应极限扩散电流密度低于H2CO3直接还原极限电流密度,通过模型计算得出的H2CO3还原反应曲线,在腐蚀电位不低于−0.8 V 的情况下几乎和总阴极极化曲线重合,此时H2CO3直接还原反应控制整个腐蚀过程,当电位达到更低的条件时,H2O 的直接还原将参与控制腐蚀。从图4 可以看出,由于低温下CO2腐蚀产物膜不易生成或者即使形成也不具有保护性,因此,即使模型中未考虑腐蚀产物膜的影响,即令ffilm为1,最终得到的预测值与实测极化曲线整体吻合情况依然较好。表3 为相应腐蚀电化学参数对比。

表3 腐蚀电化学参数Tab.3 Corrosion electrochemical parameters
耿亚楠等在80◦C对N80 碳钢进行了不同CO2分压下的电化学行为研究。当不考虑腐蚀产物膜对传质扩散的影响时,利用机理模型对其极化曲线进行预测。预测值与实测值的对比结果见图5。
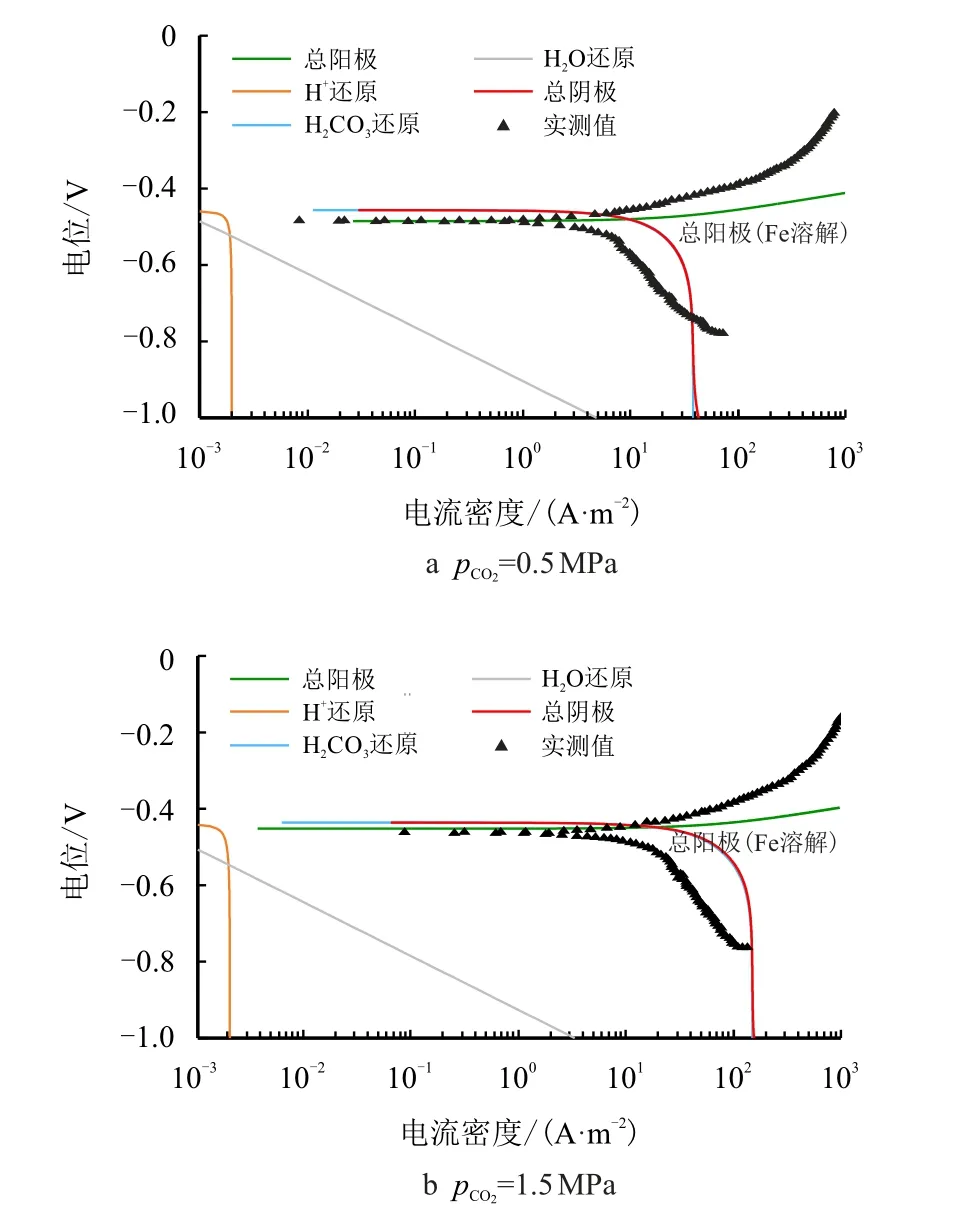
图5 动电位扫描极化曲线实测值[34] 和模型预测(T=80 ◦C)Fig.5 Experimental data[34] and model prediction of potentiodynamic sweep(T=80 ◦C)
根据图5 可知,在较高的温度和CO2分压下,未考虑腐蚀产物膜影响的预测模型在相应的实验条件下,计算得到的极化曲线与实测值相比,预测所得腐蚀电流密度明显偏高。这是由于高温高压下形成了保护性较强的腐蚀产物膜导致的,因此,利用该温度下实验所测腐蚀电流对腐蚀产物膜影响因子进行计算,计算结果见表4。由于腐蚀产物膜厚度对腐蚀速率的影响较小,根据相关文献产物膜厚度可取定值15µm[35]。将计算所得腐蚀产物膜影响因子代入模型中对两种不同CO2分压下N80 钢的腐蚀电化学行为进行预测,与实验数据对比见图6,修正模型前后的腐蚀电化学参数见表5。

表4 腐蚀产物膜影响因子计算结果Tab.4 Calculation results of corrosion product film influence factors
通过表5 和图6 可知,利用腐蚀产物膜影响因子对高温高压环境下传质扩散系数进行修正后,模型预测极化曲线和相应腐蚀电化学参数值均得到了较好的改善,腐蚀电流密度相对误差控制在10%以内,属于合理范围。图6 中阳极极化曲线预测与实测情况相差较大,这可能是由于机理模型中阳极Tafel斜率仅考虑了温度的影响,忽略了钢材的影响所致。Nesic 等研究表明,当阳极参考电位为−0.488 时,不同钢种的交换电流密度相差可以达到一个数量级,因此,忽略钢材种类对阳极电化学的影响在一定程度上会加大阳极反应预测误差[16]。
图6 动电位扫描极化曲线实测值[35] 和修正后模型预测(T=80 ◦C)Fig.6 Experimental data[35] and the revised model prediction of potentiodynamic sweep(T=80 ◦C)
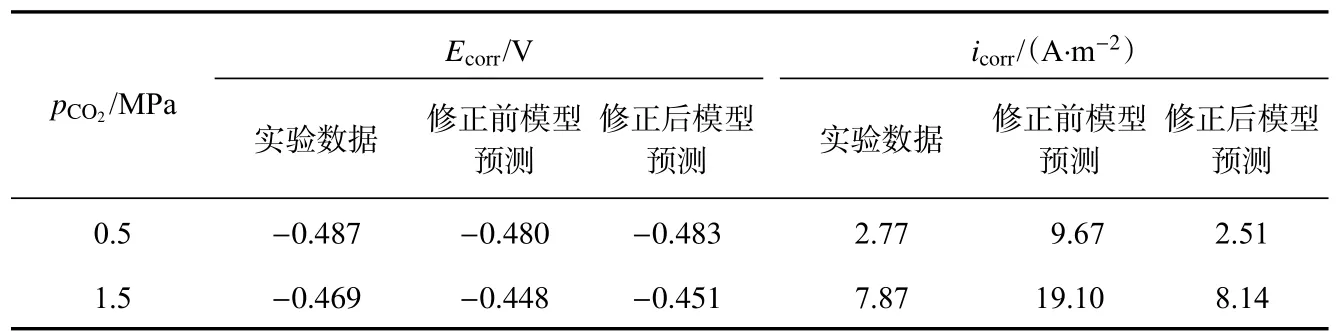
表5 修正模型前后的腐蚀电化学参数Tab.5 Corrosion electrochemical parameters before and after modification
3.2 腐蚀速率预测对比验证
图7 为20 号钢在三叠系油藏现场水样中腐蚀速率随温度的变化趋势,其中,红色曲线为未考虑腐蚀产物膜影响的模型预测结果。
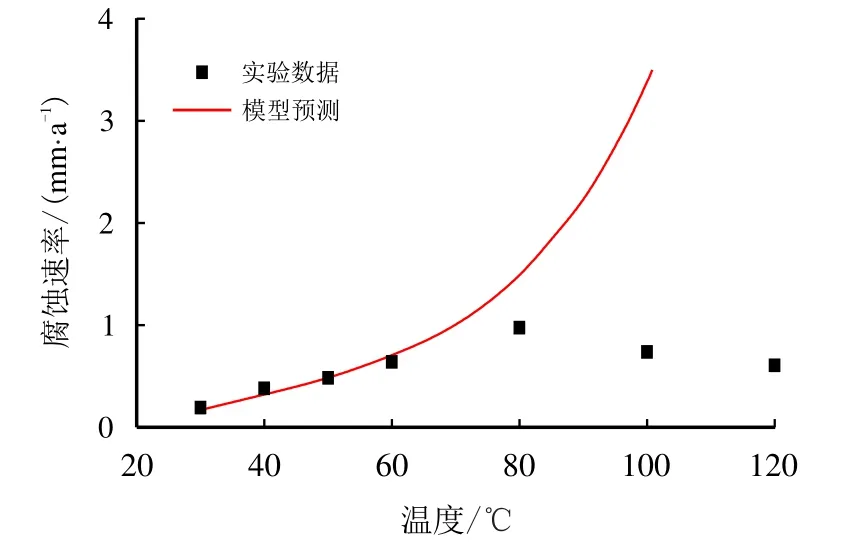
图7 腐蚀速率随温度变化实验数据[36] 与模型预测(pCO2=0.1 MPa,v=1.5 m/s)Fig.7 Experimental data[36] and model prediction of corrosion rate varying with temperature(pCO2=0.1 MPa,v=1.5 m/s)
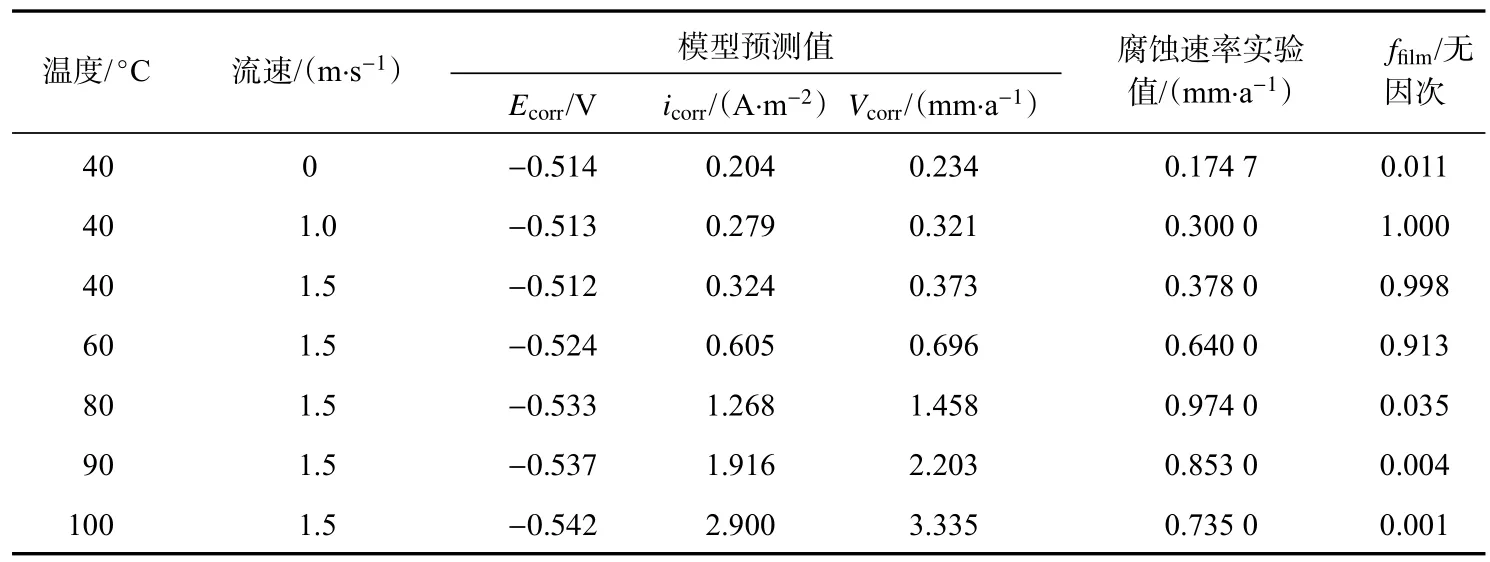
表6 腐蚀产物膜影响因子计算(pCO2=0.1 MPa)Tab.6 Calculation of corrosion product film influence factors(pCO2=0.1 MPa)
当流速一定时,腐蚀产物膜影响因子拟合曲线见图8。利用该因子对离子扩散系数进行修正,可实现预测模型的有效校正,模型校正后腐蚀速率随温度变化的模型预测和实验数据对比见图9。

图8 流速为1.5 m/s 时腐蚀产物膜影响因子随温度变化拟合曲线Fig.8 Fit curve of influence factor of corrosion product film with temperature change at flow rate of 1.5 m/s
为了进一步对模型进行验证,利用40◦C不同流体流动速度下的实验数据对预测结果进行验证分析,模型校正前后腐蚀速率随流速变化的模型预测和实验数据对比见图10。
根据图9 和图10 可知,考虑腐蚀产物膜对离子传质的阻碍作用,利用腐蚀产物膜影响因子可有效修正高温、低流速下腐蚀模型预测结果偏高的情况,在流体流动影响下和不考虑腐蚀产物膜影响的预测模型相比更为接近实际腐蚀速率。由于上述腐蚀环境的pH 值为弱酸性,流动条件下20 号钢腐蚀速率相对于流速变化并不敏感,因此,相较于温度而言,腐蚀速率随流速变化的趋势较为缓慢。修正后的腐蚀速率预测值相对于实验数据仍存在较小的误差,这是由于参与腐蚀产物膜影响因子拟合计算的数据点较少,拟合精度略低导致的。计算表明,该因子的细微变化可能导致腐蚀速率预测结果产生较大误差,因此,可获取的现场或实验工况下的腐蚀数据越多,对腐蚀产物膜影响因子的拟合计算就越准确,模型的修正效果越好。
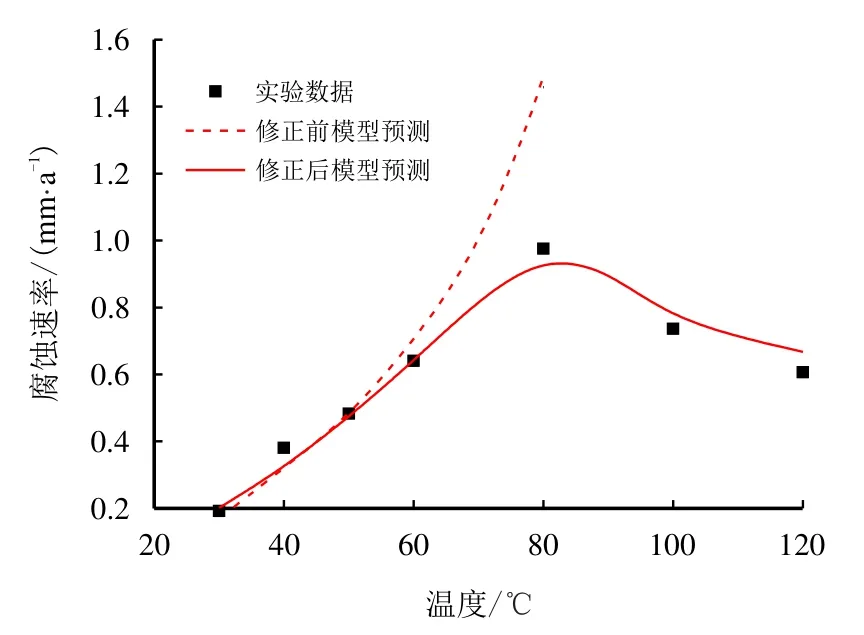
图9 腐蚀速率随温度变化实验数据[36] 与修正前后模型预测(pCO2=0.1 MPa,v=1.5 m/s)Fig.9 Experimental data[36] and the revised model prediction of corrosion rate varying with temperature(pCO2=0.1 MPa,v=1.5 m/s)
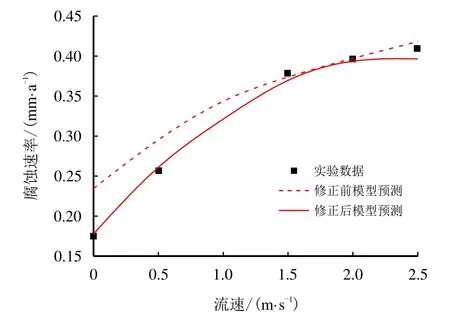
图10 腐蚀速率随流速变化实验数据[36] 与修正前后模型预测(pCO2=0.1 MPa,T=40 ◦C)Fig.10 Experimental data[36] and the revised model prediction of corrosion rate varying with flow rate(pCO2=0.1 MPa,T=40 ◦C)
由于文献中可参考实验数据有限,式(22)的适用范围仅为20◦C 1)基于腐蚀热力学及动力学理论,考虑流体流动、电化学反应及传质过程等多场耦合作用,在Nesic 等研究的基础上引入腐蚀产物膜影响因子,提出了新的腐蚀预测机理模型。计算结果表明,模型预测与实验数据吻合情况良好,在腐蚀产物膜存在的条件下能够实现腐蚀预测速率的有效修正,提高了CO2腐蚀预测机理模型的适用性和准确性。 2)腐蚀产物膜影响因子的细微变化可能导致腐蚀速率预测结果产生较大误差,因此,相应现场或实验条件下可获取的腐蚀数据越多,该因子的拟合计算精度越高,模型的修正效果就越好,能有效避免腐蚀产物膜存在下理论模型预测值偏高的情况。 3)腐蚀预测模型并未考虑较高总压下亨利定律适用性的问题和钢材种类对阳极交换电流密度的影响,因此,电化学行为预测存在一定误差。因此,可对CO2溶解度预测模型进行研究,并通过电化学实验测定CO2腐蚀环境下不同钢种的阳极交换电流密度,建立阳极交换电流密度参数表,从而进一步提高机理模型预测的准确性。4 结论
