低渗透油藏五点法井网见水时间计算方法研究

李承龙 ，孙鹏鹏，王一飞，杨桂南

1.中国石油大庆油田公司勘探开发研究院，黑龙江 大庆163712 2.黑龙江省油层物理与渗流力学重点实验室，黑龙江 大庆163712

引言

随着高品位油田剩余可采储量不断减少，低、特低渗透油田储量已成为原油产量的重要接替对象。低、特低渗透油田储层物性差，储量丰度低、产量低，开发成本高，油井见水后，含水快速上升，效果变差[1-2]。为了提高油田的开发效果，需要根据见水规律及开发时间采取有效的调整措施，抑制含水上升，提高单井及区块产量。因此，准确预测采油井及区块见水时间，对油田高效开发具有重要的现实意义。

通过调研，已有见水时间计算模型存在以下几点不足：1）在储层发育特征及流体渗流规律方面，低渗透油藏储层非均质性强，同时受压敏效应影响显著[3-5]，渗透率损失严重，引起启动压力梯度发生动态变化，已有成果未同时考虑非均质性、压敏效应和启动压力梯度动态变化等因素[6-10]。2）在措施调整方面，低渗透油田储层物性差，现场常采用压裂引效促效措施增产，已有成果未考虑压裂措施影响[11-14]。3）在井网方面，低渗透油田往往采用大井距、小排距的布井方式开采，而已有成果未考虑井距、排距不等的情况[15-20]。基于以上原因，目前见水时间模型计算结果与矿场实际差距较大，无法准确描述低渗透油藏主要特点，适用性较差。

针对低、特低渗透油田开发期间存在的矛盾问题，基于五点法井网裂缝与井排角度、裂缝长度、井距排距等因素，分析注采关系，在不同裂缝与井排角度条件下，划分裂缝与各方向注水井间流场计算单元，结合文献[21-22]，得到注采井间主流线附近流管束流量方程及见水时间表达式，针对低、特低渗透储层平面非均质性，归一化各方向注采井间基质渗透率，在此基础上，推导出采油井各个方向上主流线附近见水时间计算模型，从而形成适合注水开发低渗透油田五点法井网见水时间计算方法。

1 模型的建立

1.1 主流线方向见水时间计算模型

由文献[21]，主流线附近流管流量表达式[21]可表示为

1.2 井间基质渗透率分布模型

考虑到渗透率非均质性，将井间渗透率进行归一化处理，定义井间基质渗透率为注采井地层系数之和与注采井有效厚度之和的比值。例如，采油井O 与注水井A 井间基质渗透率可表示为

1.3 油井压裂条件下见水时间计算模型

假设裂缝方向与井排方位夹角为θ，裂缝长度为2F，井距为L，排距为d。由于采油井进行了压裂，将井与井的驱替关系转化为井与缝的驱替关系，各方向注水井与裂缝距离最短，因此，各方向注入水主流线均指向裂缝，计算各方向的见水时间可转化为计算裂缝见水时间。结合人工裂缝规模，划分各方向上缝控计算单元，划分为I、II、III和IV 共4 个单元，其中，I 与III 单元相同，II 和IV单元相同。

1.3.1 当方位角0≤θ ≤arctan（dL−1）时

图1 为方位角0≤θ ≤arctan（dL−1）时，缝控计算单元划分情况。

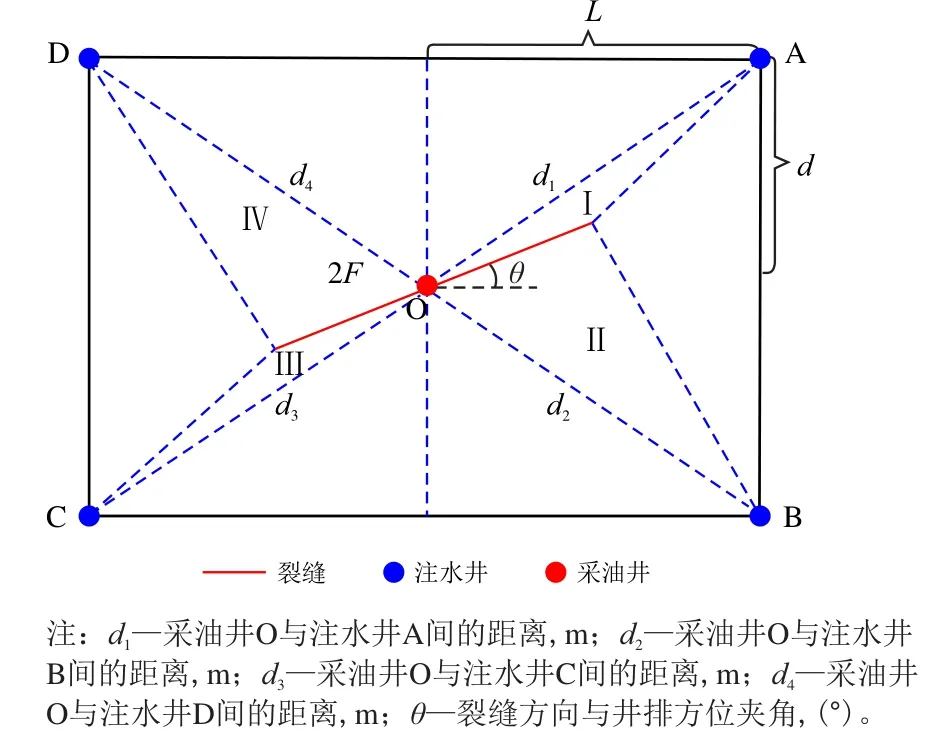
图1 当方位角0≤θ ≤arctan（dL−1）时缝控单元划分示意图Fig.1 The division of producer and injector unit on 0≤θ ≤arctan（dL−1）

1）A 井见水时间

图2 为I 区计算单元示意图，根据图2 可计算得到裂缝与O 井和A 井间连线的夹角、采油井O与注水井A 间的距离、裂缝上任意一点与注水井的距离。

图2 I 区计算单元示意图Fig.2 Calculation unit of Area I

I 区内流管束截面积可表示为

其中，0≤l≤F，rw≤ξ ≤dL

则，裂缝上任意位置的流管束流量为

式中：∆qI—裂缝上任意位置的流管束流量，m3/d；

Kw—水相相渗，无因次；

pAiwf—注水井A 井底压力，MPa。

将式（7）代入式（8），积分并化简得到

将式（7）和式（9）代入式（2），得到

将式（10）积分并化简，得到注水井A 方向的见水时间计算模型

2）B 井见水时间

图3 为II 区计算单元示意图，由图3 可得

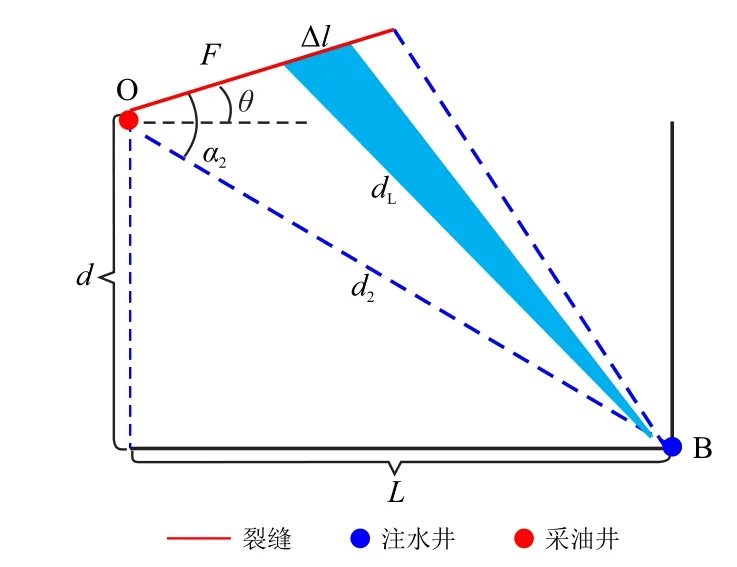
图3 II 区计算单元示意图Fig.3 Calculation unit of Area II

流管束截面积可表示为

其中，0≤l≤F，rw≤ξ ≤dL

则，裂缝上任意位置的流管束流量为

将式（15）和式（16）代入式（2），并令∆l→0，整理可得，II 区内采油井见水时间计算模型

3）C 井方向及D 井方向见水时间

C 井方向计算单元与A 井方向计算单元相同，B 井方向计算单元与D 井方向计算单元相同，可计算出C 井和D 井方向见水时间。

4）各方向见水时间计算通式

基于各方向的见水时间模型，可以总结出不同裂缝与井排角度条件下各方向的见水时间通式，如式（18）所示

根据以上推导，可得到方位角0≤θ ≤arctan（dL−1）时模型参数取值情况（表1）。

表1 0≤θ ≤arctan（dL−1）时参数取值Tab.1 Parameter value when 0≤θ ≤arctan（dL−1）

1.3.2 当方位角arctan(dL−1)<θ ≤π/2 时

图4 为方位角arctan(dL−1)<θ ≤π/2 时，缝控计算单元划分情况。从图4 可以看出，随着裂缝与井排角度的增大，各方向缝控计算单元发生变化，各方向注水井与裂缝间的距离也发生明显变化，裂缝与A 井和C 井距离增大，裂缝与B 井和D 井距离变小。当裂缝与井排角度达到π/2 时，各方向注水井与裂缝距离相等。

基于图4 缝控单元划分示意图，按照1.3.1 部分计算步骤，可推导出裂缝任意点处见水时间通式[与式（17）相同]，模型参数取值见表2。

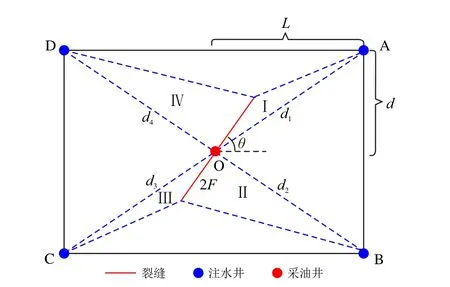
图4 当方位角arctan(dL−1)<θ ≤π/2 缝控单元划分示意图Fig.4 The division of producer and injector unit on arctan(dL−1)<θ ≤π/2

表2 arctan(dL−1)<θ ≤π/2 时参数取值Tab.2 Parameter value when arctan(dL−1)<θ ≤π/2

1.3.3 当方位角π/2<θ ≤π −arctan(dL−1)时

图5 为方位角π/2<θ ≤π −arctan(dL−1)时，缝控计算单元划分情况，从图中可以看出，随着裂缝与井排角度的增大，各方向缝控计算单元发生变化，各方向注水井与裂缝间的距离也发生明显变化，裂缝与B 井和D 井距离增小，裂缝与A 井和C 井距离变大。当裂缝与井排角度达到π −arctan(dL−1)时，裂缝与B 井和D 井距离最小。

基于图5 缝控单元划分示意图，按照1.3.1 部分详细公式推导过程及相应计算步骤，可推导出各方向见水时间通式[与式（17）相同]，模型参数取值见表3。

表3 π/2<θ ≤π −arctan(dL−1)时参数取值Tab.3 Parameter value when π/2<θ ≤π −arctan(dL−1)

图5 当方位角π/2<θ ≤π −arctan(dL−1)时缝控单元划分示意图Fig.5 The division of producer and injector unit on π/2<θ ≤π −arctan(dL−1)

1.3.4 当方位角π −arctan(dL−1)<θ ≤π 时

图6 为方位角π −arctan(dL−1)<θ ≤π 时，缝控计算单元划分情况，从图中可以看出，随着裂缝与井排角度的增大，各方向缝控计算单元发生变化，各方向注水井与裂缝间的距离也发生明显变化，裂缝与B 井和D 井距离增大，裂缝与A 井和C 井距离变小。当裂缝与井排角度达到π 时，各方向注水井与裂缝距离相等。

基于图6 缝控单元划分示意图，按照1.3.1 详细公式推导过程及相应计算步骤，可推导出各方向见水时间通式[与式（17）相同]，模型参数取值见表4。

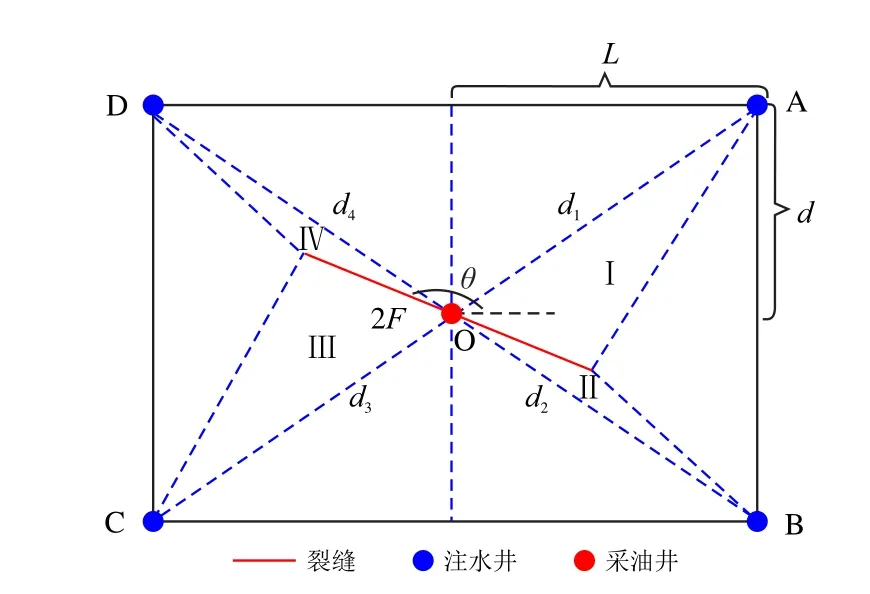
图6 方位角π −arctan(dL−1)<θ ≤π 时缝控单元划分示意图Fig.6 The division of producer and injector unit on π −arctan(dL−1)<θ ≤π

表4 π −arctan(dL−1)<θ ≤π 时参数取值Tab.4 Parameter value when π −arctan(dL−1)<θ ≤π

则采油井见水时间为

2 实例分析

以长垣外围某低渗透区块为研究对象，利用该区块数据分析不同因素对见水时间的影响规律。该区块采用300 m×300 m 五点法井网，油层埋深959.9 m，注水井A、B、C、D 及采油井O 渗透率分别为5，10，20，30 和20 mD，注采井有效厚度均为4 m，原始地层压力为8.4 MPa，注入压力为13.1 MPa，采油井井底流压为2.3 MPa，井筒半径为0.127 m，含水饱和度为55%，水相相对渗透率为0.9，含水上升速度为2.86%，裂缝长度为100 m，裂缝与井排角度为0◦，原油黏度8 mPa·s，综合含水为80%，压敏系数等参数见文献[6]。

2.1 井距与排距之比影响

图7 为井距和排距之比与见水时间的关系曲线，井距与排距之比越大，注入井与裂缝间驱替距离越小，见水时间越早。当井距与排距比小于2.0时，单井见水时间变化幅度较大，当井距与排距比大于2.0 时，单井见水时间基本不变。

图7 井距和排距之比与见水时间关系曲线Fig.7 Relationship between ratio of well spacing and row spacing and water breakthrough time

2.2 压敏效应影响

图8 为压敏效应与见水时间的关系曲线，压敏效应对见水时间影响较小，随着压敏效应影响程度增大，采油井见水时间略有增加。压敏效应影响程度增大，注采井间驱替压力越小，注入水渗流速度变小，见水时间变晚。

图8 压敏效应与见水时间关系曲线Fig.8 Relationship between pressure-sensitive effect and water breakthrough time

2.3 非均质性影响

图9 为非均质性与见水时间的关系曲线，整体上，储层非均质性越强，采油井见水时间越早。注入水沿高渗透方向突进越厉害，当储层非均质性越强，沿高渗透方向突进的速度越快。

图9 非均质性与单井最早见水时间关系曲线Fig.9 Relationship between heterogeneity and earliest water breakthrough time of single well

2.4 裂缝方向与井排方位夹角影响

图10 为裂缝方向与井排方位夹角与各方向平均见水时间的关系曲线。整体上，随着裂缝方向与井排方位夹角的增大，见水时间呈波动性变化。当裂缝方向与井排方位夹角为100◦时，见水时间推迟，当裂缝方向与井排方位夹角大于140◦时，见水时间提前。随着裂缝方向与井排方位夹角变化，注入井与裂缝距离发生变化，总体上，驱替距离呈波动性变化，导致见水时间呈波动性变化。

图10 裂缝方向与井排方位夹角与各方向平均见水时间关系曲线Fig.10 Relationship between fracture and well row angle and average water breakthrough time in all directions

2.5 裂缝长度影响

图11 为裂缝长度与见水时间的关系曲线，由图11 可以看出，随着裂缝长度的增加，见水时间越早。裂缝长度越大，注入井与裂缝距离越小，驱替距离越小，采油井见水早。当缝长小于100 m 时，见水时间变化明显，当缝长大于等于100 m 时，见水时间变化幅度小。

图11 裂缝长度与见水时间关系曲线Fig.11 Relationship between crack length and water breakthrough time

2.6 启动压力梯度影响

图12 为启动压力梯度与见水时间的关系曲线，随着启动压力梯度的增加，见水时间推迟。启动压力梯度越大，需要克服渗流阻力越大，渗流速度越小，见水时间越晚。

图12 启动压力梯度与见水时间关系曲线Fig.12 Relationship between start-up pressure gradient and water breakthrough time

2.7 原始地层压力影响

图13 为原始地层压力与见水时间的关系曲线，整体上随着原始地层压力的升高，见水时间推迟。渗透性较差的区域受压敏效应影响较大，由于采油井井底附近压力较低，原始地层压力越高，井底附近渗透率损失越严重，引起启动压力梯度变大，详见文献[6]中式（3）∼式（5），渗流阻力增加，渗流速度变小，采油井见水变晚。

图13 原始地层压力与见水时间关系曲线Fig.13 Relationship between original formation pressure and water breakthrough time

2.8 原始含水饱和度影响

图14 为原始含水饱和度与见水时间的关系曲线，当原始含水饱和度在0.4∼0.5 时，见水时间较早，当渗透率小于0.4 或大于0.5 时，见水时间推迟。分析其原因：随着原始含水饱和度的增加，含水上升速度先升后降，说明注入水突进速度呈相同趋势变化，导致原始含水饱和度与采油井见水时间关系曲线呈先降后升趋势变化。

图14 原始含水饱和度与见水时间关系曲线Fig.14 Relationship between original water saturation and water breakthrough time

3 结论

1）基于低渗透油藏渗流理论，推导了低渗透油藏五点法井网见水时间计算模型，与传统模型相比，所建模型综合考虑了压敏效应、变启动压力梯度、排距井距、裂缝与井排角度、裂缝长度、非均质性、含水饱和度及相渗等因素，更符合矿场实际。

2）根据裂缝与井排角度、缝长及井距排距等因素，分析井网注采关系，简化裂缝与注水井间流动单元形状，建立了主流线长度计算公式、流管束截面积计算公式及流量计算公式。

3）根据各井点基质渗透率和有效厚度，归一化各方向上的基质渗透率，实现了五点法井网非均质性。

4）利用本文推导模型，分析了各因素对见水时间的影响规律。成果可用于指导低渗透区块开发调整方案的编制，为低渗透油藏的有效动用提供理论保障。