粤港澳高中数学“数与代数”模块的比较研究*
2023-05-08广东省广州市第二中学510000孙晓荣
广东省广州市第二中学(510000) 孙晓荣
1 问题的提出
代数模块的学习始终贯穿小学—初中—高中三个学段,它是研究数、数量、关系、结构与代数方程(组)的通用解法及其性质的数学分支.中学数学以及现代数学中很多问题需要借助代数,如函数,方程与不等式等为工具来解决,其成为培养学生数学运算,抽象概括,逻辑推理,数学建模以及问题解决等核心素养的重要载体.
2019年2月18日党中央、国务院同意正式公开发布《粤港澳大湾区发展规划纲要》[1],这份纲领性文件中提出要打造粤港澳大湾区教育和人才高地.关于基础教育方面,提出要加强基础教育交流合作.基于这样的现实需要,现以粤港澳三地最新的高中数学课程标准为研究对象,针对“数与代数”模块为主题,主要从学习要求方面进行比较研究,以期在对比中得到一些启示,从而对我们正在进行的课程改革提供一定的参考.
2 研究对象与方法
2.1 研究地区和数学课程标准版本的选择
广东地区是基础教育改革的重要地区, 目前采用的是2020年6月发布的《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》),该版本是在《普通高中数学课程标准(2017年版)》的基础上,基于2018年9月全国教育大会和2019年10月十九届四中全会对教育改革的体系建设和目标方向提出的新要求而修订的.我国香港特区采用的是香港课程发展议会与香港考试及评核局于2018年3月修订的《数学课程及评估指引(中四至中六)》(以下简称《指引》).我国澳门特区采用的是澳门教育青年局在2014年公布, 并于17-18 学年实行的《澳门高中数学学力基本要求》(以下简称《要求》).
2.2 研究内容与方法
针对三地课标中对高中数学课程内容的描述,我们主要对“函数”,“数与数系”,“代数式,方程与不等式”与“数列”四大知识单元的内容进行比较研究.通过梳理共同点与差异,为“新课标”的实施提供思考和启示.研究主要采用比较、内容分析等研究方法.
3 高中数学课程标准中“数与代数”模块的比较与分析
3.1 粤港澳三地“函数”部分的比较
粤港澳三地的课程标准中,函数内容发展的主线基本相同: 定义—性质—基本初等函数,其中基本初等函数包括指数函数、对数函数、幂函数、三角函数.

表1 必修课程中函数单元的结构比较
(1)粤港澳三地分别从运动变化观点,用集合语言与对应关系刻画函数,建立完整的函数概念,体会集合语言与对应关系在刻画函数概念的作用,了解构成函数的三要素.粤澳两地均强调在实际情境和具体实例中,会根据不同的需要选择恰当的方法表示函数.粤地区则更强调数学建模的观点,能用函数构建模型,解决问题.
对于分段函数, 粤澳两地均提出了解简单的分段函数,并能直接应用,而香港地区对分段函数无具体要求.
关于反函数,澳门要求学生理解反函数的概念,并理解指数函数y=ax(a >0,a≠ 1)与对数函数y= logax(a >0,a≠ 1)互为反函数,而粤港两地对反函数的要求不高,广东只要求学生知道指数函数y=ax(a >0,a≠ 1)与对数函数y= logax(a >0,a≠ 1)互为反函数,不要求一般地讨论反函数的形式化定义.香港则未提“反函数”的概念,但有明确要求学生知道y=ax与y= logax对称于y=x.显然,澳门对“反函数”的学习要求更高,注重强调反函数的定义域和值域正好是原函数的值域与定义域.
(2)粤《标准》更注重学生掌握运用函数性质求解方程近似解的基本方法(二分法),理解函数构建数学模型的过程,和运用模型思想发展和提出问题,分析和解决问题.香港在“续函数图像”明确把“从表列、符号和图像的角度理解函数的平移和伸缩变换”作为学习重点,粤澳两地均无明确要求.
(3)粤港澳三地都要求学生重点认识二次函数,指数函数,对数函数,理解并认识以上各类函数的定义,性质及图像.香港地区只要求学生理解二次函数的图像特征,对一般幂函数的的学习无具体要求.广东地区的要求也只是了解幂函数,结合的图像,理解它们的变化规律.而澳门对幂函数的概念及上述函数图像的图像和性质均为理解,要求比粤港两地要高.
结合《标准》对教学内容要求层次的划分方式,并参考布卢姆教育目标分类学,本文按认知要求维度的分类为: 了解、理解、掌握与灵活运用,并在统计时规定水平权重分别为1、2、3、4.在香港《指引》中出现“欣赏”的认知要求,在记录时划分为“了解”层次.下面着重对指数函数以及对数函数的内容做一个比较分析:

表2 粤港澳三地指数函数的知识点及认知要求的统计
粤港澳三地对指数函数部分设计的知识点数差不多,但还是存在一些小差别.一是粤港两地在课程设置时均是遵从“指数幂—指数函数”,“对数—对数函数”,而澳门是在“学习组别A-2: 数与式”中统一学习了“指数幂、根式和对数”的概念,并充分理解其运算后,才在“学习组别A-5: 函数”中依次进行“指数函数和对数函数”的学习.二是澳门比粤港两地多了“根式的性质”及“根式的运算”的学习,澳门要求能对含有无理数的分式进行化简,能用公式进行无理数和根式之间的四则运算,能对分母中含有的式子进行化简,可见澳门更重视代数的恒等变换;三是粤澳两地都提出结合实例了解指数函数的实际背景,体会指数函数是一种重要的数学模型,而广东更重视指数函数图像的发展态势,要求能结合现实情境中的具体问题,理解“指数爆炸”的现实含义,如人口增长问题等.而香港则在高中必修课程延伸部分的单元一(微积分与统计)中把“指数函数的应用”列为重点学习内容,还提出学生须解包括复利息、人口增长和放射性元素的衰变有关的应用题.

表3 粤港澳三地对数函数的知识点及认知要求的统计
不难发现,粤澳两地对数函数的学习要求均低于指数函数,而香港对两者的学习要求维持稳定,而澳门在“学习组别A-2: 数与式”中明确要求理解对数概念与指数概念的对应关系,掌握两者的相互转化,这也为澳门对“反函数”较高的认知要求做了铺垫.
(4)从课程标准上看,粤港两地均把三角函数部分纳入代数范畴去讨论, 用函数观点处理三角函数, 借助正弦、余弦、正切等三角函数图像,了解三角函数的周期性、单调性、奇偶性,而澳门把三角函数放在几何范畴,作为学习组别的“B-5 三角”系统的某一部分,这样的设置更加系统,突出三角学自身的内在联系和性质,把三角和它的几何应用联系起来,而广东则是把正,余弦定理设置在平面向量的章节.香港其实把正余弦函数和正切函数放在必修的“续三角学”部分,并同时设置了利用代数方法和图解法解三角方程,以作为三角函数的应用,而粤澳两地在必修中设置的复角公式等内容,香港则把它放在了选修课程单元二的基础知识中的“续三角函数”部分.
从下表可以看出, 香港在三角部分的知识点涉及更多,深度更大,一旦学生选择了延伸课程单元二的学习,则必须要掌握余割、正割和余切函数,那么相对应的同角三角函数关系就多了1+tan2θ= sec2θ和1+cot2θ= csc2θ,同时还需要理解正、余弦函数的和积互化,而粤澳两地均未涉及这些知识点的教学.但香港地区对知识点y=Asin(ωx+φ)的图像及性质并不涉及.
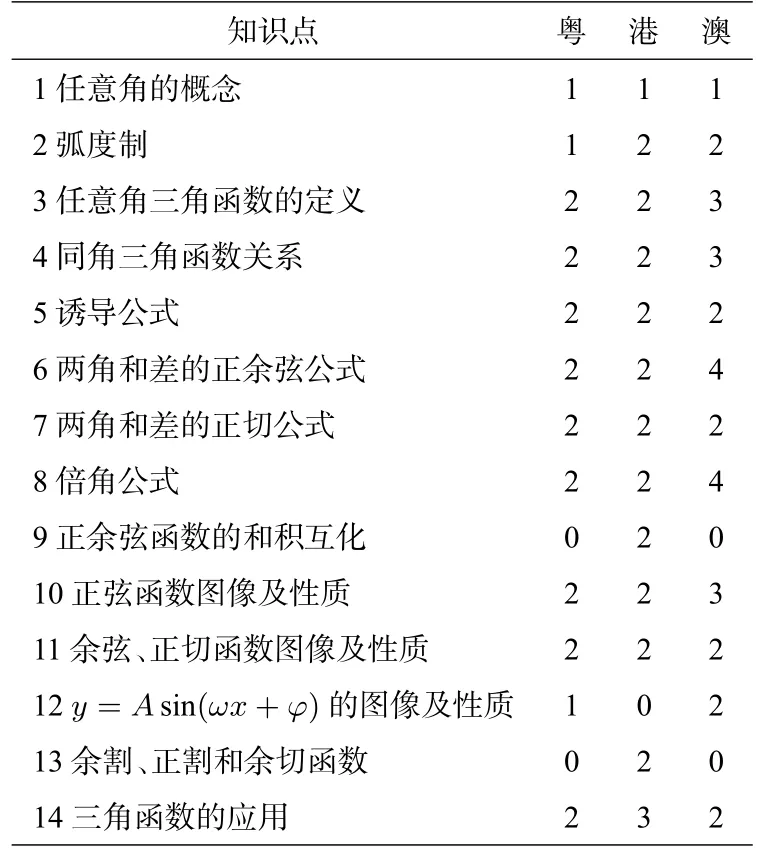
表4 粤港澳三地三角函数的知识点及认知要求的统计
澳门比粤港两地更注重公式的推导和熟练运用,对两角和差的正余弦公式和倍角公式更是要求“掌握”并能“熟练应用”,而广东明显对三角函数部分做了精简,无反三角函数和三角方程的学习,只在同角三角函数关系处要求理解,而在诱导公式及三角恒等变换处只要求经历推导过程,知道公式并明确不要求记忆.
在应用层面,粤《标准》更注重利用三角函数构建刻画事物周期变化的数学模型,而港澳更侧重于三角学的几何应用.
3.2 粤港澳三地“数与数系”部分的比较
在“数与数系”部分,我们主要比较三地对“复数”内容学习深度,其中香港要求最低,只需学生“欣赏复数系的发展,进行复数的加、减、乘和除运算”;广东要求稍高,除对复数代数表示式的四则运算有要求外,还需要学生理解复数和复数加减运算的几何意义和两个复数相等的含义;澳门是从复平面的构造出发引出复数,要求学生从不同角度理解复数,如复数的向量形式和三角形式,还要求学生认识复数的三角形式以及复数的乘除、乘方和开方运算,体会其带来的方便.
3.3 粤港澳三地“式”、“方程”与“不等式”部分的比较
香港在必修课程中“数与代数范畴”有专门的学习单位“续多项式”,要求“进行多项式除法”,“理解余式定理和因式定理”,“理解最大公因式和最小公倍式的概念”“进行有理函数(代数分式)的加减乘除”.澳门在必修“学习组别A-2数与式”部分对“式”的要求更加系统,除了“理解多项式的概念,了解综合除法,理解余式定理”,还要“了解多项式的基本定理”,“运用数值代入法和比较系数法求待定系数”,“了解立方和与差的公式”及“体会多项式知识在求解方程的根中的应用”,并且澳门把“指数幂,根式与对数”的学习统一在该组别学习.而广东在高中课程中没有单独的模块学习“式”.
三地在“方程”部分的差异主要是内容的广度,因为广东主要在初中安排“方程”的学习, 特别是一元二次方程的解法, 二次方程根与系数的关系以及由已知根建立二次方程,而香港则是在高中加强了这一块;广东高中阶段方程的学习主要是在初高中衔接内容中出现,主要是复习和熟练一元二次方程的解法,着重于从函数观点理解,其他方程如指对方程,三角方程也都是在对应函数的学习下,结合函数去理解,在《标准》中除了对一元二方程有要求,对其它方程并无具体要求.而港澳地区对方程的学习更加系统,香港有专门的“续方程”模块,澳门有专门的“学习组别A-3 方程”,两地涉及方程的类型的学习更多,广度更大,如下表所示:

表5 粤港澳三地方程类型的统计
广东把“不等式”部分的内容安排在“主题一预备知识”中,很明显是作为衔接课程的一部分,只要求学生“从函数观点看一元二次不等式”“理解不等式的概念”,“掌握不等式的性质”,“掌握基本不等式及能用基本不等式解决简单的最大或最小值问题”,而香港的学习重点是方程的解法的学习,澳门在“学习组别A-4: 不等式”部分涉及的不等式类型更多,如下表所示:
粤澳两地都设置了“基本不等式”的知识点,澳门从基本不等式本身的“证明过程”到基本不等式的应用于其他题目的证明和求解都有较高的要求;三地都很重视“一元二次不等式”,因为“一元二次不等式”是广东初中阶段的重点学习内容,解法已经学习过,在高中阶段更侧重于从函数观点看一元二次不等式.港澳则侧重于解法的学习(判别式法,因式分解法),而澳门和广东都注重三个“二次”的联系; 三地只有澳门设置了含有绝对值不等式和一元高次不等式的学习,但要求较低,只需求解简单的含有绝对值不等式和了解可用“数轴”求解已进行因式分解的一元高次不等式;港澳对二元一次不等式(组)及线性规划都有要求,而广东则删减了这部分内容的学习.

表6 粤港澳三地不等式类型的统计
3.4 粤港澳三地“数列”部分的比较
粤澳两地都强调了解数列的概念及以列表、图像、通项公式的表示方法,注重从函数观点处理数列,粤《标准》更是把数列放在选择性必修的“主题一函数”,目的就是希望学生认识到数列是一种特殊的函数,并“体会等差数列与一次函数,等比数列与指数函数的关系”,澳门更明确要求“理解数列的递推公式,能根据递推公式写出数列的前几项,并能归纳猜想除某些数列的通项公式”,而广东在《标准》并未有此要求;三地都着重于“等差数列与等比数列”的学习,对其“概念,性质,通项,求和”都需要理解并应用,粤澳两地更重视利用数列模型解决实际问题,在公式的学习上,广东更注重等差、等比通项公式和前项和公式的探索过程.
4 参考与启示
4.1 学考统一,要求明确
香港《指引》是香港课程发展议会与香港考试及评核局联合制定的法定文件, 利于执行上的学考一致, 同时港《指引》中有对“学习重点”的“诠释”,对难易和复杂性作了控制,要求明确,比如会使用一些限定性的语句“只修读基础课题的学生不须简化诸如的根式”,也会提示“解诸如等较复杂方程的应用题属非基础课题,并在学习重点5.4 中处理”等等.而粤《标准》由课程中心研制,广东参加的高等学校招生全国统一考试则由考试院负责,比如“三角恒等变换”部分,《标准》明确指出积化和差、和差化积与半角公式不要求记忆,但学生面临的问题就是,不记忆公式,看似降低了学习难度,实际上更让他们感到困惑,因为考试要求在这一部分并不低.同样有此问题的还有“不等式”部分,《标准》对“基本不等式”地要求是“能解决简单的最大或最小值问题”,但实际学生遇到的问题并不简单,甚至很难.如何使得“学”和“考”统一协调? 还是有值得改进的地方.
4.2 重视衔接课程,体现连贯性
粤港澳三地都很重视初高中的衔接,澳门的衔接课程比较注重基础计算能力的训练,澳门对高中涉及的“数与式”做了统一的学习组别,为后续的运算做准备;香港《指引》在基础课程部分由浅入深,逻辑联系和整体性较强,比如学生熟悉的“一元二次方程”,从“因式法解方程”开始,到通过“判别式”的研究,直接引入复数,对数系进行扩充;而粤《标准》则把“数系的扩充”放在“主题三”中作为单独的模块,但实际的课程引入仍然是通过方程的解;再比如通过对一元二次方程根的几何意义入手,进而研究一元二次函数的图像特征,并在此处提出重点要求学生会“代数方法求二次函数的极大和极小值”,而“极大(小)值”的概念在《标准》中是在选择性必修“一元函数的导数”部分才提及,如果在前面学生熟悉的函数的学习中先接触此类容易理解的高等数学的部分概念,学生是否在建立知识框架的时候更为连贯与清晰?
4.3 评估“代数力”,提高运算要求
广东高中学生的知识储备和计算能力参差不齐,“根式运算”“立方和差公式”“综合除法”等在实际学习过程其实都需要,但这些知识点在有些初中并未涉及,就会导致学生的学习障碍,粤《标准》并未在这一块做明确要求,而澳门一直重视“代数力”的培养,统一在《要求》中对“数与式”做了具体的学习要求,这是值得我们参考的.
