依据操作差异 完善除法含义——人教版教材二年级下册“包含除”教学实践研究

□徐 霞 李嫣红 俞佳丽

在“平均分”相关内容的教学中，学生学习了“等分除”，再学习“包含除”会相对简单一些。那么，如何激发学生利用已有知识经验，通过“分一分”“记一记”“列一列”，得到“包含除”的表达形式？如何创设教学情境，将“包含除”与“等分除”进行比较，让学生发现同样的除法算式有不同的含义？如何让学生通过比较，理解等分除是指把一个数平均分成几份，求每份是多少，包含除是指一个数里面包含了几个几，从而构建起除法的含义与数量关系的联系？与之相应的除法运算，又可以迁移运用哪一些方法，需要从哪一些角度进行丰富？基于这样的思考，笔者进行了课堂教学实践。

一、进行比较，提炼除法含义

“平均分”有两种不同情况，一种是“等分”，一种是“包含”。在“平均分”的教学中，教师已经让学生通过具体情境直观感知了这两种情况。在“等分除”的教学中，则结合具体操作活动，将“等分”的连减形式转化成除法中的“等分除”。在此基础上，本内容通过题组比较，让学生认识除法中的“包含除”。

（一）阅读审题，发现异同

教师先出示题组：（1）把24 个竹笋平均放在4个盘子里，每个盘子里放多少个？（2）有24个竹笋，每4 个放一盘，可以放几盘？接着引导学生思考：这两个问题有什么相同的地方与不同的地方？

学生通过比较、思考指出，都是把24个竹笋平均分，但第（1）题是“平均放在4 个盘子里”，而第（2）题是“每4 个放一盘”。还有学生指出第（1）题是求每份数，第（2）题是求份数。根据学生的回答，教师归纳：第（1）题是已知总数、份数，求每份数；第（2）题是已知总数与每份数，求份数。

（二）操作记录，发现关系

学生已经有了从连减的形式中概括出除法算式与数量关系的经验。因此，教师可以让学生依据发现的不同点，用连减的形式分别记录分的过程，并列出数量关系和相应的除法算式。学生独立完成后反馈评析，教师通过板书形成图1 的两种形式。

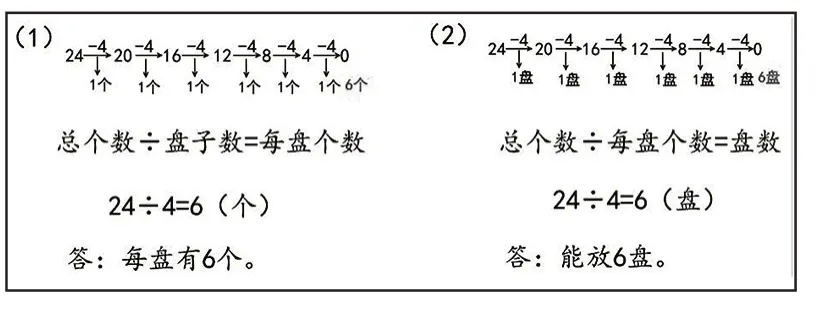
图1

接着，让学生比较两种形式，说一说有哪些不同的地方。依据学生的回答，教师进一步总结：第（1）题中的除法算式是把24 平均分成4 份，求每份是多少；第（2）题中的除法算式是求24 里面有几个4。

（三）回顾比较，形成结构

通过题组比较，学生初步感知除法的两种含义。教师进一步引导学生回顾“平均分”学习中的题组并与之比较，让学生依据学习经验，列出数量关系与除法算式，进一步概括除法的两种含义。

教师先出示题组：（1）把18 个橘子平均装在6个盘子里面，每个盘子里面可以装几个？（2）有18个橘子，每个盘子放6 个，可以放这样的几盘？接着让学生读题，并出示分一分与算一算的过程（如图2、图3），指出这是学习“平均分”时的两道题目，请学生重新分析其中的信息与问题，说一说它们各表示什么意思，并列出数量关系与算式解答。学生独立完成后反馈，重点辨析“等分除”与“包含除”的区别。

图2

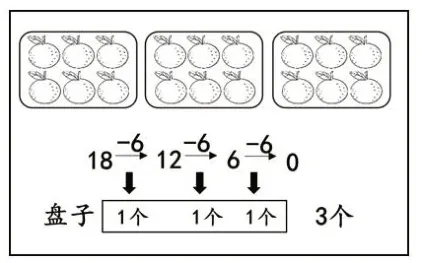
图3

上述教学，教师引导学生回顾比较操作活动中的“等分”和“包含”，以“等分除”的表达经验引出“包含除”，让学生在具体情境的比较中，通过操作活动、连减形式记录与数量关系分析，多角度感知“等分除”与“包含除”的联系与区别。

二、看图编题，体会除法含义

结合具体情境，学生经历了从具体操作、连减形式记录到除法概括的过程，对除法的两种含义已经有了一定的认识。下面让学生结合具体图式，根据信息与问题编写解决问题，概括出相应的除法含义，列出数量关系并解答除法算式。

（一）区别类型，感受不同

教师出示图4，请学生依据图意，说一说已知什么信息，要解决什么问题。先学生独立完成，再同桌交流，最后全班反馈。学生编出了两道解决问题：（1）有18 个小圆片，把它们平均分成3 组，每组有多少个？（2）一共有14个灯泡，每个灯座装2个灯泡，可以装几个灯座？教师引导学生依据图式编写相应的解决问题，让他们进一步感知除法两种含义的区别，即第（1）题是把18平均分成3份，求每份是多少，第（2）题是求14里面有几个2。

图4

（二）依据特征，自主解答

很显然，学生在依据图式提出问题的过程中，已经掌握了两类除法解决问题的特征。在此基础上，教师请学生一边操作，一边依据特征列出数量关系并解答算式。学生独立完成后，教师进行反馈评析，形成如图5的解答过程。

图5

相比于乘法，除法的数量关系更加复杂。因此，为了让学生区分两种不同的除法含义，教师不断地采用题组的形式，让学生结合图式、关键词等，逐步发现两类除法含义在表达上的不同点，为进一步概括两类除法的名称做好了铺垫。

（三）归纳名称，寻找对应

教师引导学生进一步回顾前面学习的三组题组（课件分步出示各题组），请学生把它们分成两类，并提问：“可以怎样分？”并让学生说一说它们各有什么特征。学习了“等分除”之后，学生已经对“等分除”的特征有了一定的认识。现在通过对三组题组的分类、比较，学生可以进一步明确“等分除”的特征，并对另一类除法的特征进行概括，即“一个数里面包含了几个几”，叫作“包含除”。

上述教学结合具体例子与数量关系，让学生感受到除法就是对平均分过程的记录。在这样的过程中，学生逐步脱离操作活动与连减形式表述，能够依据“等分除”和“包含除”的含义列出数量关系，代入信息后再用乘法口诀求商的方法进行计算。

三、分层练习，加深除法理解

除法的学习包含了解意义、计算与解决问题。在这三方面内容的学习中，学生围绕平均分这一基本概念，对除法已经有了一定的认识。在此基础上，让学生进行专项练习，不断地提升学生对除法的理解。

（一）想乘做除，熟练计算

教师出示8道除法计算题，请学生利用乘法口诀计算出商。

（1）48÷8=（2）63÷7=（3）42÷7=（4）54÷9=

（5）35÷7=（6）72÷9=（7）72÷8=（8）56÷8=

学生独立完成后，教师进行反馈评析，接着请学生回答：这8道题与“等分除”中的除法计算题相比，有什么不一样的地方？学生发现数据好像更复杂一些。教师解释这些题目都是“用7～9 的乘法口诀求商”的，“等分除”中的除法计算题都是“用2～6的乘法口诀求商”的。

很显然，在整体教学设计的背景下，可以把原来相互独立的除法含义、除法运算与用除法运算解决问题融合在一起。其中，除法运算中的利用乘法口诀求商，是“乘法口诀”的再应用，把它与除法含义的学习融合，能使求商的方法更科学。

（二）融入情境，列式释义

图6

教师出示图6，让学生说一说图中有哪些信息，据此可以提出什么问题。这是一个开放性问题，学生可以先提出问题：每串香蕉有5根，7串一共有多少根？然后列式解答：5×7=35（根）。再把总根数看成已知信息，提出问题：（1）一共有35 根香蕉，平均分成7 串，每串有多少根？（2）一共有35 根香蕉，每串有5 根，一共有几串？分别列式解答，并说明每一个问题的类型，即乘法是“求几个几是多少”，第（1）题是“等分除”，第（2）题是“包含除”。

除法是乘法的逆运算。一个乘法算式可以改写出两个除法算式，相应地，一个乘法数量关系也可以对应两个除法数量关系。利用这种关系，可以帮助学生更好地理解除法的含义，以及乘除法解决问题的结构体系。

（三）乘除综合，提升能力

把除法含义与解决问题相联系，把用除法运算解决问题与用乘法运算解决问题相沟通，可以从整体的视角认识除法，更加深刻地认识除法含义与用除法运算解决问题之间的关系。

教师出示有联系的题目：二（1）班同学参加春游活动，分成了9个小组，每个小组有4人，二（1）班一共有多少人？如果6人一个小组，可以分成几个小组？让学生独立读题解答，完成后反馈评析。在解答第2 个问题时，学生列式：36÷6=6（组）。教师提问：“这两个‘6’分别表示什么意思？这是一道什么类型的除法题？”学生思考后发现，这两个“6”的含义不同，其中除数“6”表示每份数，商“6”表示份数，属于“包含除”。

很显然，本内容的练习巩固，并不是简单地对“包含除”的巩固，而是从整体的视角把前面学习的除法运算与除法数量关系进行适当拓展，使除法运算与乘法口诀建立紧密的联系，与乘法形成“一图式三算式（一个乘法算式两个除法算式）”的结构，为从乘法数量关系中延伸出除法数量关系做好铺垫。

数学学习的过程是一个不断完善、丰富和形成结构的过程。在本内容的教学中，既要关注新知——包含除，也要与“等分除”建立联系，完善对于除法含义的理解。只有这样，学生所学的知识才是有结构的、网状联结的、逐步丰盈完善的。